改進的蒸發波導RSHMU 模型及預測性能分析

張利軍 李建儒 王紅光 韓杰 張超 張守寶

（中國電波傳播研究所, 青島 266107）

引 言

大氣波導是發生在對流層大氣中的一種異常折射現象，能夠顯著改變電磁波的正常傳播特性，對雷達、通信等電子設備產生重要影響. 大氣波導分為蒸發波導、表面波導和懸空波導. 海上蒸發波導是由近海面水汽隨著高度迅速下降形成，其發生概率極高，可達80%以上. 由于近海面近地層大氣具有明顯的湍流特征，各個氣象要素瞬時值難以測量，因此通常不采用構建大氣折射率廓線的方法來確定蒸發波導高度，而是根據海洋大氣近地層相似理論，利用海面水文要素和近海面氣象要素的觀測來計算蒸發波導高度. 自20 世紀60 年代以來，伴隨著微氣象學的發展，基于莫寧相似理論相繼提出了Jeskes 模型[1]、Rotheram 模型[2]、Fairall 模型[3]、LKB 模型[4]、Paulus-Jeskes 模型[5]、 MGB 模型[6]、BYC 模型[7]、NPS 模型[8]以及偽折射率模型[9]等. 文獻[10]利用張強、胡隱樵給出的局地相似函數給出了局地相似蒸發波導模型.文獻[10]在不穩定條件下采用Babin 蒸發波導模型，穩定條件下采用局地模型，二者組合給出了新蒸發波導模型.

20 世紀80 年代，基于海上試驗結果，前蘇聯的相關學者也提出了相關的蒸發波導模型；并基于相關理論研究成果，研制了利用大氣波導實現超視距的雷達. 直到2007 年，烏克蘭科學院無線物理與電子 研 究 所 的V. K. Ivanov 院 士 以 及V. N. Shalyapin和Yu. V. Levadnyi 發表了基于標準氣象數據確定蒸發波導高度的論文，對前蘇聯提出的RSHMU 模型[11]有了一定介紹. 文獻[12]糾正了文獻[11]及相關文獻[13-14]存在的錯誤的溫度剖面穩定度函數，給出了不同風速以及不同相對濕度(relative humidity, RH)條件下的敏感性分析結果，并與渤海梯度塔觀測數據進行了比較. 結果表明：不穩定條件下該模型優于美國海軍研究生院提出的NPS 模型；而穩定條件下該模型劣于NPS 模型，存在較大誤差. 由于RSHMU模型在穩定條件下采用線性函數，適用范圍有限，對水文氣象數據輸入過于敏感，可能出現不合理的診斷結果，因此不便使用.

本文首先引入穩定條件下發展的新的穩定度函數，給出不同表達式對應的改進蒸發波導模型預測性能. 借鑒Paulus 給出的訂正方法[5]，給出改進的RSHMU 蒸發波導預測模型，及基于不同風速和不同RH 的敏感性分析結果，顯著改善了穩定條件下的預測性能，并利用渤海梯度塔觀測數據給出了其預測性能.

1 RSHMU 模型預測原理

具體的粗糙度方案計算可參見文獻[12]. RSHMU模型采用與NPS 模型一致的方法，基于莫寧相似理論首先計算出位溫剖面及比濕剖面，再利用絕熱遞減率確定溫度剖面、流體靜力學公式及理想氣體定律聯合確定壓強剖面以及利用水汽壓與比濕關系確定水汽壓剖面，最后計算出修正折射率剖面，選擇修正折射率最小值對應的高度即為蒸發波導高度.

其中壓強剖面按照如下關系確定[15]：

2 已有模型存在問題及改進的RSHMU模型

由于RSHMU 模型在穩定條件下采用了簡單的線性普適函數形式，且在部分風速以及部分RH 條件下可能出現湍流不適用的情形，因此在氣海溫差(air-sea temperature difference, ASTD)大 于 零 的 情 形下會出現蒸發波導高度診斷不合理的現象. 如圖1以及圖2 所示，在海表溫度(sea surface temperature,SST)為25 ℃以及15 ℃條件下出現蒸發波導高度迅速增加的情形，進而導致該模型過于敏感，在實際使用中出現不便. 文獻[16]提出利用穩定條件下的剖面穩定度函數對Babin 蒸發波導模型進行改進，利用鐵塔平臺實測氣象數據研究改進后的模型在穩定層結條件下的預測效果. 因此本文首先嘗試利用不同的穩定度函數對RSHMU模型改進給出敏感性結果.

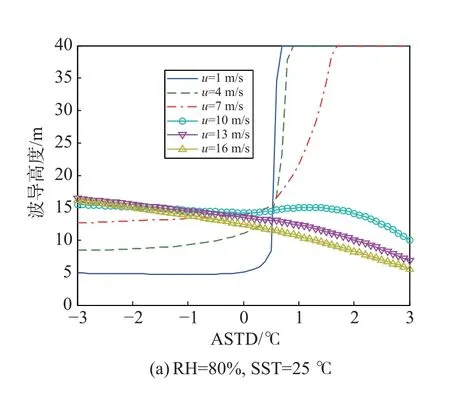
圖1 不同風速條件下RSHMU 模型計算的蒸發波導高度隨ASTD 的變化Fig. 1 Variation of evaporation duct height calculated by RSHMU model with ASTD at different wind speed conditions

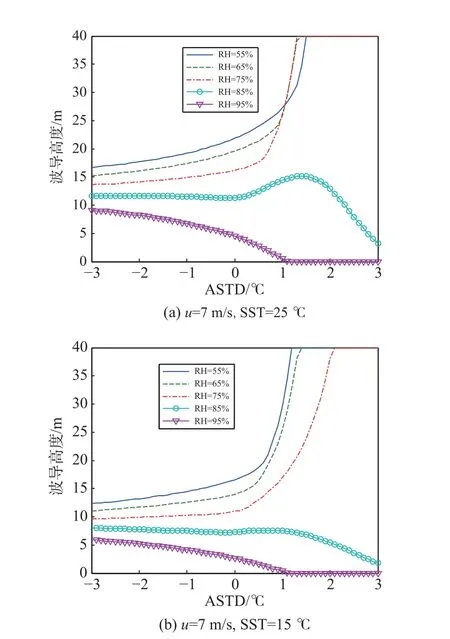
圖2 不同RH 條件下RSHMU 模型計算的蒸發波導高度隨ASTD 的變化Fig. 2 Variation of evaporation duct height calculated by RSHMU model with ASTD at different RH conditions

針對穩定條件下的剖面穩定度函數，Holtslag 等[17]給出了HDB88 相似函數形式. RSHMU 模型采用與HDB88 相似的函數形式，只是系數有所差異.

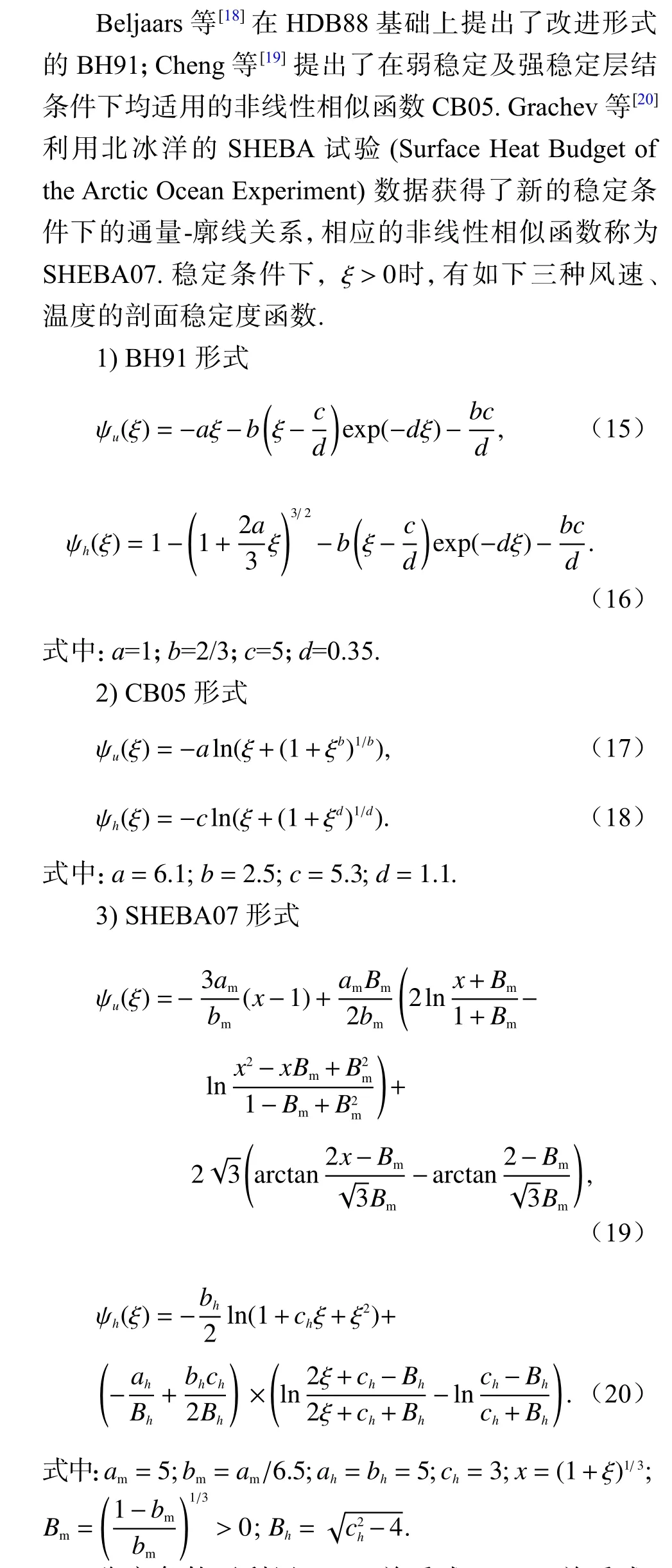
穩定條件下利用BH91 關系式、CB05 關系式、SHEBA07 關系式替換簡單的線性函數，即可獲得不同形式改進的RSHMU 模型，簡稱為RSHUMUBH91模型、RSHUMU-CB05 模型、RSHUMU-SHEBA07.利用穩定條件替換的剖面穩定函數獲得的改進RSHMU模型預測性能如圖3～5 所示. 可以看出，BH91 關系式相對已有線性關系式改善不大，而CB05 以及SHEBA07關系式有一定改善，但蒸發波導高度迅速增加的情形卻沒有改善.

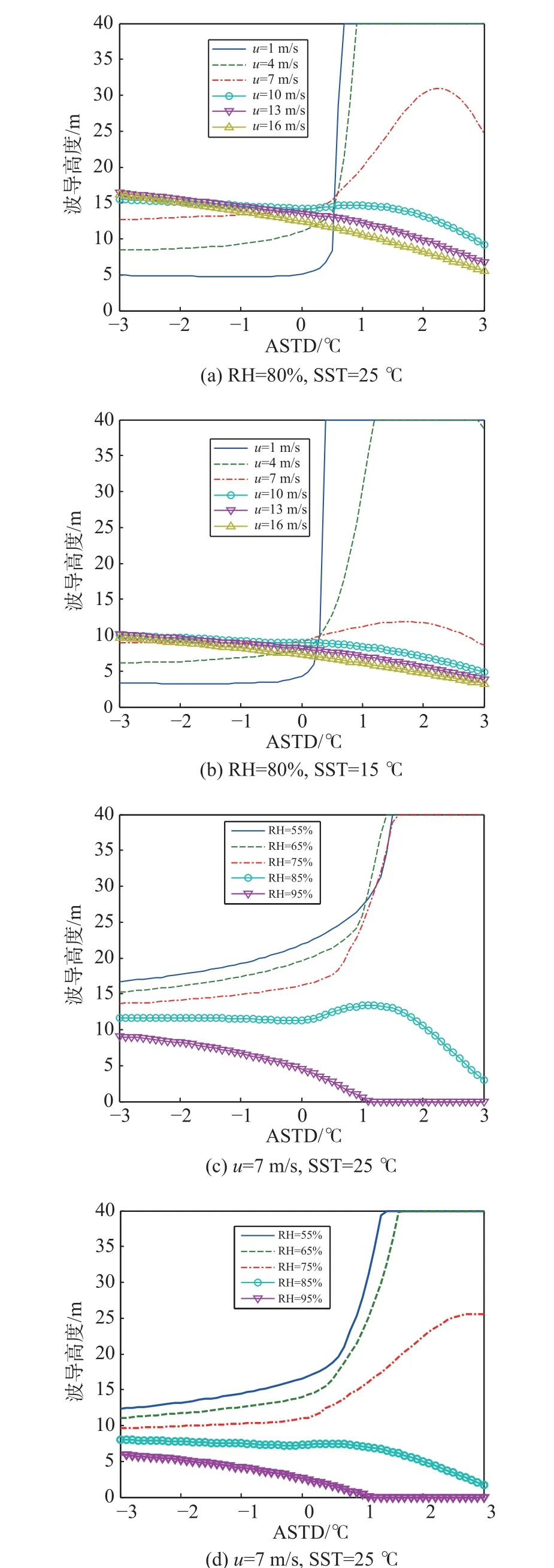
圖3 BH91 剖面穩定度函數修正Fig. 3 BH91 profile stability function correction

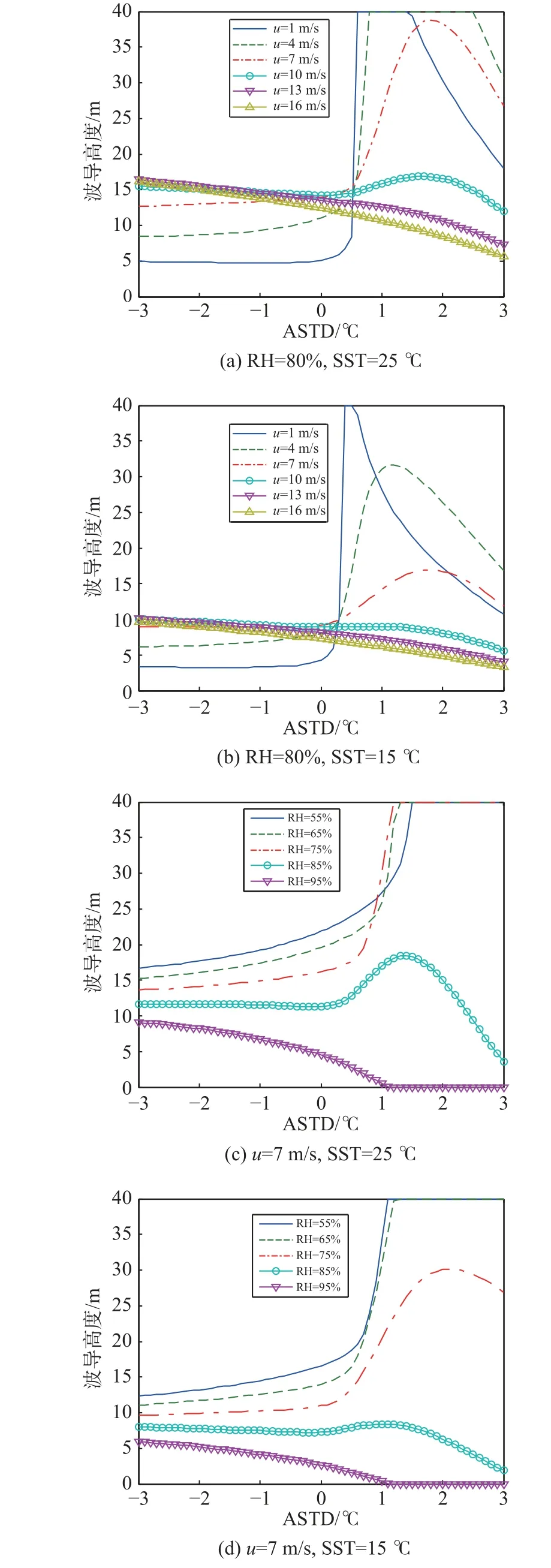
圖4 CB05 剖面穩定度函數修正Fig. 4 CB05 profile stability function correction

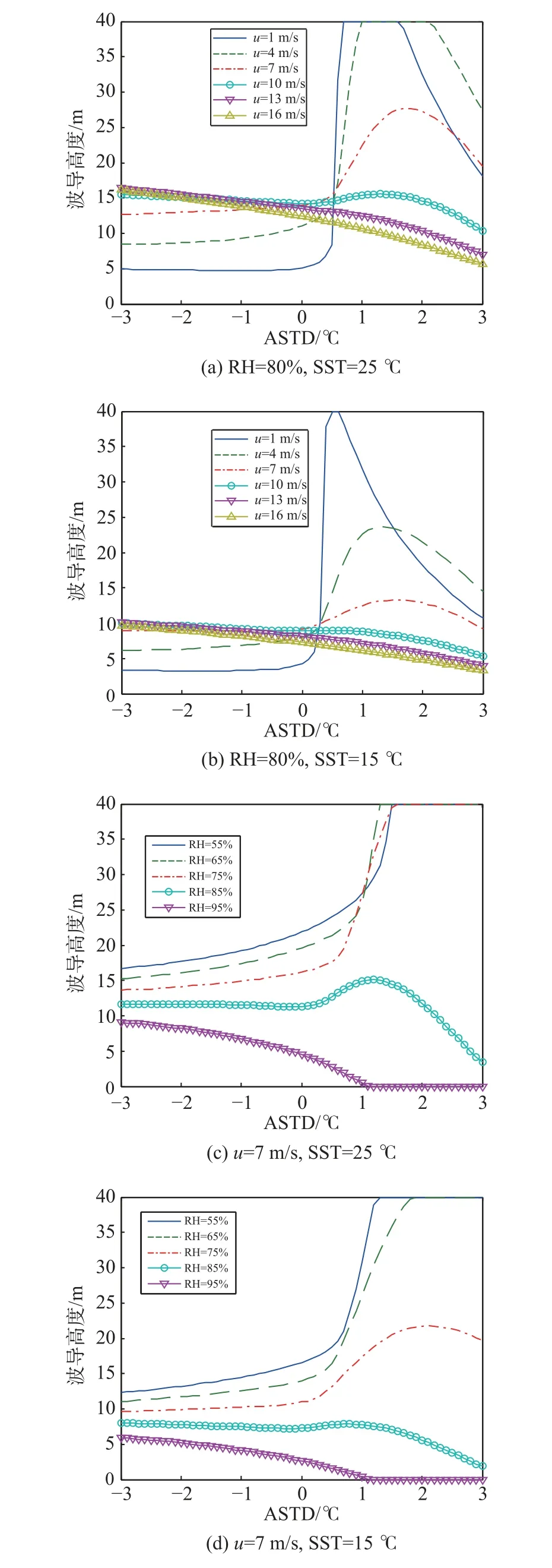
圖5 SHEBA07 剖面穩定度函數修正Fig. 5 SHEBA07 profile stability function correction

文獻[5]指出：當ASTD 小于-1 ℃時，基于蒸發波導高度及模理論計算的傳播損耗與實測傳播損耗具有較好的對應關系；當ASTD 大于-1 ℃時，對蒸發波導高度計算方法進行適當改進，獲得了計算傳播損耗與實測損耗比較一致的結果. 本文借鑒這一方法，ASTD 小于-1 ℃時，采用RSHMU 模型計算方法；當ASTD 大于-1 ℃時，保持海溫不變，利用RSHMU 模型分別計算ASTD 等于-1 ℃及等于0 ℃的蒸發波導高度h-1及h0. 如果h0＞h-1，則蒸發波導高度為h-1，否則依照原來的氣溫與海溫來計算蒸發波導高度. 這種改進的RSHMU 模型可稱之為P-RSHMU模型，預測流程如圖6 所示.選取SST 25 ℃以及15 ℃，ASTD -3～3 ℃，以0.1 ℃為間隔，即可獲得不同的空氣溫度，對應不同的穩定性條件. 假定測量高度為6 m，取RH 80%，壓強1 010 hPa，風速分別選擇1、4、7、10、13、16 m/s，利用P-RSHMU 模型計算的蒸發波導高度隨ASTD變化的仿真結果如圖7 所示. 可以看出，相對圖1 來說，P-RSHMU 模型顯著改善了穩定條件下不合理的蒸發波導高度結果.

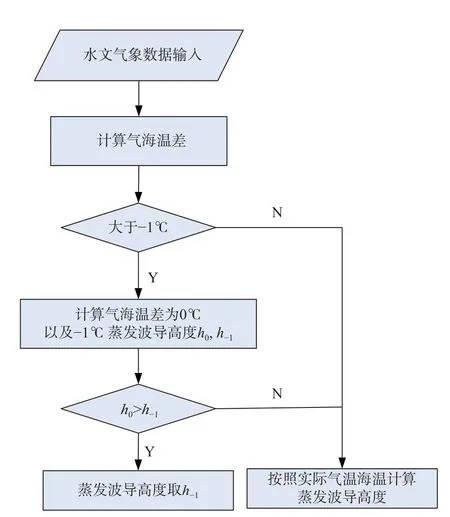
圖6 P-RSHMU 模型預測流程Fig. 6 Prediction flowchart for P-RSHMU model

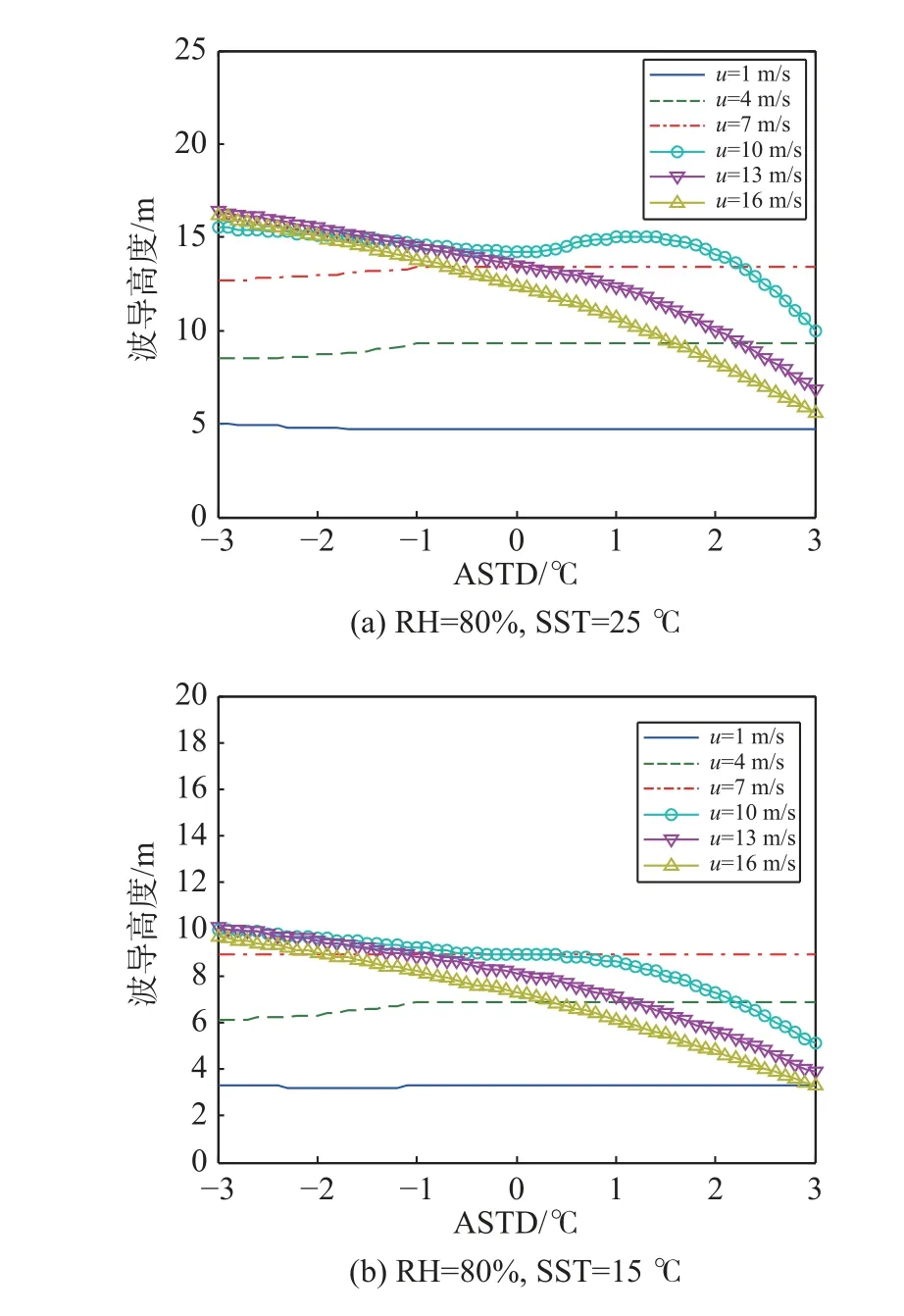
圖7 不同風速條件下P-RSHMU 模型計算的蒸發波導高度隨ASTD 的變化Fig. 7 Evaporation duct height calculated by P-RSHMU model variation with air-sea temperture difference at different wind speed conditions

假定測量高度為6 m，取風速7 m/s，壓強1 010 hPa，RH 分別取55%、65%、75%、85%和95%，利用PRSHMU 模型計算的蒸發波導高度隨著ASTD 變化的仿真結果如圖8 所示. 可以看出，蒸發波導高度隨著RH 的增加而顯著下降，相對圖2 來說顯著改善了穩定條件下的不合理結果. 因此從電波傳播應用來說，這種簡單的方法一定程度上解決了穩定條件下采用簡單線性函數存在的問題，有效抑制了蒸發波導高度迅速增加的情形.

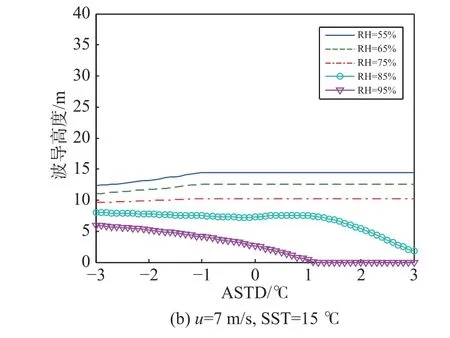
圖8 不同RH 條件下P-RSHMU 模型計算的蒸發波導高度隨ASTD 的變化Fig. 8 Variation of evaporation duct height calculated by PRSHMU model variation with air-sea temprature difference at different RH conditions

3 P-RSHMU 模型預測性能分析

基于2011 年6 月30 日至8 月5 日采集的梯度實測數據計算獲得的蒸發波導高度，同時利用10 m 高度處采集的水文氣象參數通過RSHMU 模型、RSHUMUBH91 模型、RSHUMU-CB05 模型、RSHUMU-SHEBA07模型以及P-RSHMU 模型預測蒸發波導高度，預測結果與梯度儀測量高度對比如圖9 所示，星號表示不穩定條件和中性條件，即ASTD≤0 的情形，圓圈表示穩定條件，即ASTD 大于0 的情形. 可以看出，不穩定條件下預測結果性能保持不變；利用穩定條件下改進的剖面函數有效抑制了蒸發波導高度為40 m的情形，但穩定條件下的預測結果仍然偏高；借鑒Paulus 修正方法給出的P-RSHUMU 模型則給出了較好的預測結果.

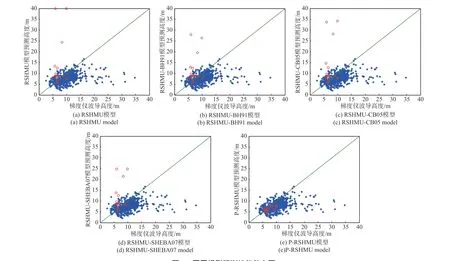
圖9 不同模型預測性能散點圖Fig. 9 Scatter plot of prediction performances among different improved models

表1 給出了改進模型及已有模型的預測誤差對比結果. 可以看出，基于渤海實測梯度塔觀測數據，穩定條件下的剖面穩定度函數修正模型RSHMUSHEBA07 相對已有模型有一定程度改善，平均誤差從7.3 m 降至5.0 m，均方根誤差從13.24 m 降至7.99 m，改善效果不明顯；而穩定條件下P-RSHMU 模型預測高度平均誤差為-1.02 m，均方根誤差為1.49 m，明顯優于已有模型. 說明改進的P-RSHMU 模型可以顯著改善穩定條件下的預測結果.

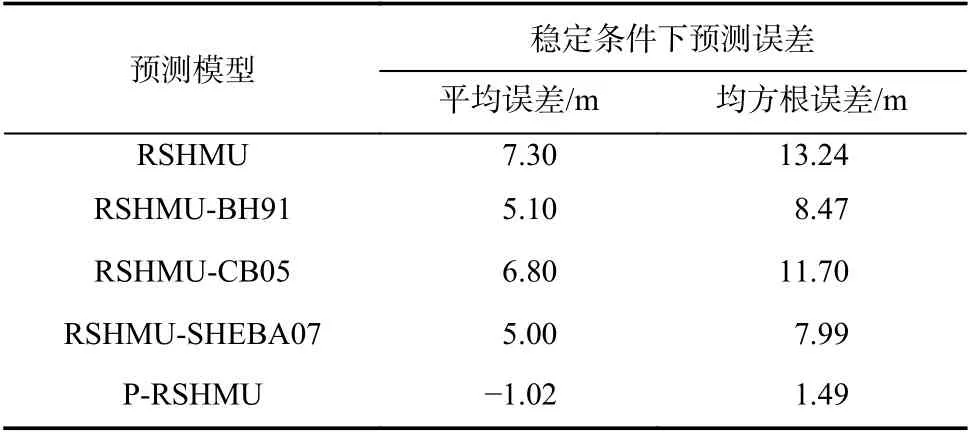
表1 不同模型預測性能對比表Tab. 1 Comparison of different models prediction performance

4 結 論

為解決穩定條件下RSHMU 模型過于敏感不便使用的問題，首先引入穩定條件下發展的剖面穩定度函數，敏感性分析結果表明這種剖面穩定度函數的改進并不能改善穩定條件下過于敏感的問題. 因此借鑒Paulus 給出的基于實測傳播損耗以及診斷波導高度計算傳播損耗的訂正方法，給出了P-RSHMU蒸發波導預測模型，有效解決了穩定條件下不合理的蒸發波導高度診斷結果. 利用渤海梯度塔觀測數據進行了P-RSHMU 預測模型的性能分析，結果表明：該改進模型在穩定條件下預測蒸發波導高度的平均誤差為-1.02 m，均方根誤差為1.49 m，顯著改善了已有RSHMU 模型的預測性能. 進一步地，可以利用該改進模型分析蒸發波導高度與動量通量、感熱通量、潛熱通量的相關性[21].