基于改進引力搜索算法的高速并聯(lián)機器人軌跡優(yōu)化

徐 巖

(綏化學院，黑龍江 綏化 152061)

高速并聯(lián)機器人被廣泛應(yīng)用于食品、醫(yī)療等諸多領(lǐng)域[1-2]。為了提高生產(chǎn)線上高速并聯(lián)機器人的工作效率，國內(nèi)外學者對其運動軌跡的規(guī)劃開展了大量的研究。張好劍等[3]將改進遺傳算法用于高速并聯(lián)機器人的路徑規(guī)劃，發(fā)現(xiàn)其能有效降低分揀行程，而且平均分揀效率較優(yōu)化前提高了14.76%；解則曉等[4]利用電機輸入電能和機器人機械能消耗兩個能耗指標，對9種軌跡優(yōu)化方法參數(shù)進行了優(yōu)化，發(fā)現(xiàn)Bang-Bang運動定律的分段多項式曲線是最優(yōu)軌跡，具有時空可重復(fù)性；章鴻[5]提出了一種基于三次樣條函數(shù)的高速并聯(lián)機器人軌跡規(guī)劃方法，該法可以改善機器人的工作空間，提高機器人末端執(zhí)行器的穩(wěn)定性；郭俊等[6]提出了一種基于蟻群算法的軌跡規(guī)劃方法，減小了末端執(zhí)行器的抖動，提高了設(shè)備運行的平穩(wěn)性。上述方法可以生成滿足各種復(fù)雜約束條件的運動軌跡，但計算效率低、穩(wěn)定性差。

基于此，研究擬將運動軌跡規(guī)劃方法用于高速并聯(lián)機器人末端執(zhí)行器的軌跡優(yōu)化，旨在為高速并聯(lián)機器人軌跡規(guī)劃方法的研究提供依據(jù)。

1 系統(tǒng)概述

圖1為高速并聯(lián)食物拾放機器人的結(jié)構(gòu)，其主要由靜平臺、動平臺、主動臂、從動臂、減速器及電機五部分組成[7]。驅(qū)動電機固定在靜平臺上，從動臂通過球鉸與動平臺連接；主動臂和從動臂組成支鏈，動平臺由主平臺和輔助平臺組成。

2 末端執(zhí)行器軌跡優(yōu)化

2.1 運動軌跡模型

在末端執(zhí)行器拾放操作過程中，拾放點的角速度和加速度為零，轉(zhuǎn)角平滑，加速度連續(xù)[8]。通過上述分析建立規(guī)劃模型。以運動時間最低和加加速度變化最小為目標，以速度和加速度在合理范圍內(nèi)為約束條件，建立多約束、多目標、非線性高速并聯(lián)機器人末端執(zhí)行器規(guī)劃模型，如式(1)和式(2)所示。

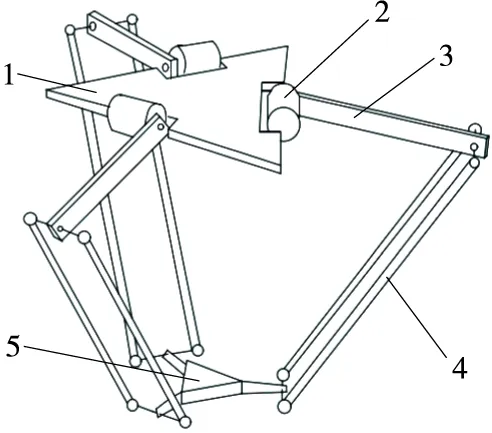
1.靜平臺 2.減速器及電機 3.主動臂 4.從動臂 5.動平臺圖1 并聯(lián)機器人結(jié)構(gòu)Figure 1 Parallel robot body

(1)

(2)

式中：

ti——靜平臺上3個驅(qū)動電機的運動時間，s；

θi——靜平臺上3個驅(qū)動電機的旋轉(zhuǎn)角度，rad；

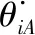
Vmax——關(guān)節(jié)最大角速度，rad/s；

amax——關(guān)節(jié)最大加速度，rad/s2。

選取權(quán)重系數(shù)k1和k2，根據(jù)特定的比例關(guān)系結(jié)合運動周期目標和加加速度目標，然后用改進算法求解模型[9]。

2.2 改進引力搜索算法

引力搜索算法(GSA)在處理優(yōu)化問題的過程中，種群中所有個體之間的信息按照萬有引力定律進行傳遞，使個體相互作用，最終聚集在一起獲得最優(yōu)解[10]。GSA具有良好的全局搜索能力。然而，GSA也存在一些問題，如早熟收斂和求解精度差等問題[11]。因此，從初始種群優(yōu)化、引力常數(shù)優(yōu)化和個體逃逸優(yōu)化3個方面進行了改進。

2.2.1 初始種群優(yōu)化 初始種群分布均勻合理，非常有利于算法求解。因此，引入了一種用于初始種群選擇的對立學習策略[12]。

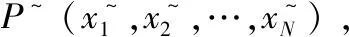
Xi=(xi1,xi2,…,xij,…,xiD)。

(3)

其中，xij∈[aj,bj]，i=1,2,…,N，j=1,2,…,D。

采用對立學習策略可以通過初始種群Rx獲得對立種群Ox，如式(4)所示[14]。

(4)

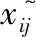
(5)

從原始種群中獲得的對立種群Ox與原始種群Rx相結(jié)合，形成新的初始種群{Rx∪Ox}。引入對立學習策略后，種群適應(yīng)度值的解不僅包括初始種群的解，還包括對立種群的解，提高了算法效率[15]。

2.2.2 引力常數(shù)優(yōu)化 參數(shù)α對G值有很大影響，通過控制參數(shù)α的值，可以間接影響加速度的變化，以控制收斂速度。將模糊控制引入?yún)?shù)α的控制中，具體步驟：

步驟1：對種群特征進行分析。引入種群豐富度RN和發(fā)展度AN，種群豐富度表示種群在解中的位置，其與個體在解中的分布有關(guān)，RN越高越不易陷入局部極值，在參數(shù)處理中，引入RN來評估搜索范圍內(nèi)個體的理想分布，如式(6)所示[16]。

(6)

式中：

N、D——個體數(shù)和維度；

RL——最遠兩個個體之間的距離；

X——個體位置；

k——迭代次數(shù)；

RN——種群豐富度，(0，1)。

根據(jù)算法中的個體適應(yīng)度值設(shè)計發(fā)展水平AN。負值表示發(fā)展方向的偏離，算法解偏離最優(yōu)解。對于模糊控制，需要評估RN、AN、k和α(t-1)，以獲得其結(jié)果α(t)。

步驟2：設(shè)定評估標準。根據(jù)需求，將隸屬度分為上、中、下三級。表1為參數(shù)RN、AN、k、α(t-1)的取值與隸屬函數(shù)的關(guān)系。

表1 不同等級參數(shù)取值范圍Table 1 Value range of different grade parameters

步驟3：參數(shù)α模糊處理策略。根據(jù)步驟1和步驟2中選擇的參數(shù)，根據(jù)表2中的策略選擇參數(shù)α值。

表2 取值規(guī)則表?Table 2 Value rule table

2.2.3 個體逃逸優(yōu)化 在GSA優(yōu)化過程中，由于初始種群選擇不足會使多個個體逃逸，在限定區(qū)分布非常密集，對算法的性能產(chǎn)生非常大的影響[17]。因此，在處理個體逃逸問題時，引入界限異變，逃逸個體xi超過上限如式(7) 所示，超過下限如式(8)所示[18]。

(7)

(8)

式中：

xmax、xmin——逃逸個體的位置上、下限，mm；

u——異變參數(shù)(根據(jù)xmax與xmin進行選擇)；

rd——隨機變量，[0,1]。

使用上述處理方法，當個體超過限值時，可以避免逃逸個體最終集中在界限上，分散算法的搜索方向，降低搜索速度。

圖2為改進引力搜索算法的流程圖。

圖2 改進引力搜索算法流程Figure 2 Improve gravitational search algorithm process

3 仿真結(jié)果與分析

3.1 仿真參數(shù)

仿真設(shè)備為華為PC，操作系統(tǒng)為windows 10 64位旗艦，11代酷睿i7 CPU，主頻2.5 GHz，內(nèi)存16 GB，仿真平臺為MATLAB r2018a[19]。表3為高速并聯(lián)機器人的基本參數(shù)。

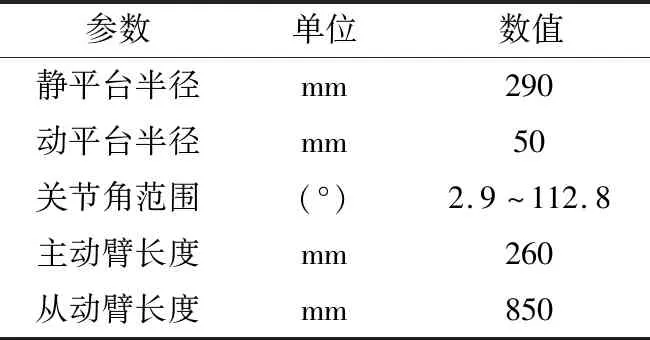
表3 機器人基本參數(shù)Table 3 Robot basic parameters

高速并聯(lián)機器人拾放路徑為高度25 mm、長度305 mm的類門字型路徑。算法約束：最大角速度Vmax=10 rad/s，最大角加速度amax=400 rad/s2。初始種群中的個體數(shù)N=40，算法的最大迭代次數(shù)為30，單次作業(yè)時長0.01～0.20 s。食品拾放對工作效率要求較高，將權(quán)重系數(shù)設(shè)置為k1=0.8，k2=0.2。

3.2 仿真分析

為了驗證試驗算法的可行性，采用標準引力搜索算法(GSA)和試驗算法分別求解了4-3-4規(guī)劃模型和5-3-5規(guī)劃模型。分析單次作業(yè)時長t(半運動周期)和加加速度的求解結(jié)果，對20次的結(jié)果進行記錄，獲得了單次操作的最短操作時間和平均操作時間，結(jié)果如表4所示。

從表4可以看出，試驗算法得到的4-3-4規(guī)劃模型最短單次運行時間為0.168 9 s，GSA的最短單次運行時間為0.172 2 s。相同算法下，4-3-4規(guī)劃模型得到的規(guī)劃結(jié)果均優(yōu)于5-3-5規(guī)劃模型的。因此，試驗算法得到的運動軌跡設(shè)計方案更符合預(yù)期要求，可以最大限度地提高機器人的性能，確保穩(wěn)定性。

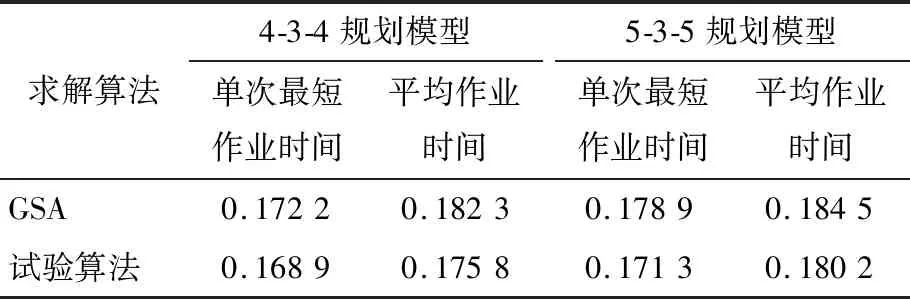
表4 不同算法的規(guī)劃結(jié)果Table 4 Planning results for different algorithms s

為了驗證試驗算法的優(yōu)越性，在4-3-4規(guī)劃模型下，進一步分析了運動周期與抑振效果的關(guān)系。加速度變化越小，對機構(gòu)振動的抑制效果越明顯，高速并聯(lián)機器人運動越穩(wěn)定。由于軌跡規(guī)劃模型還包括運動周期的時長，有必要分析兩者之間的關(guān)系。

設(shè)置不同的k1和k2系數(shù)，并將其代入模型中，通過改進算法求解模型，單次作業(yè)周期曲線和加加速度變化曲線如圖3和圖4所示。

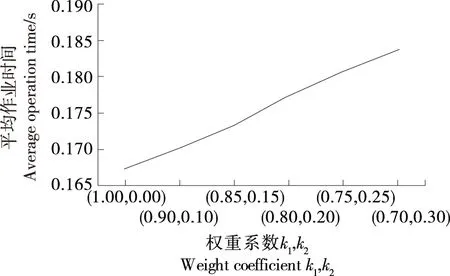
圖3 單次作業(yè)時長變化曲線Figure 3 Single operation time change curve

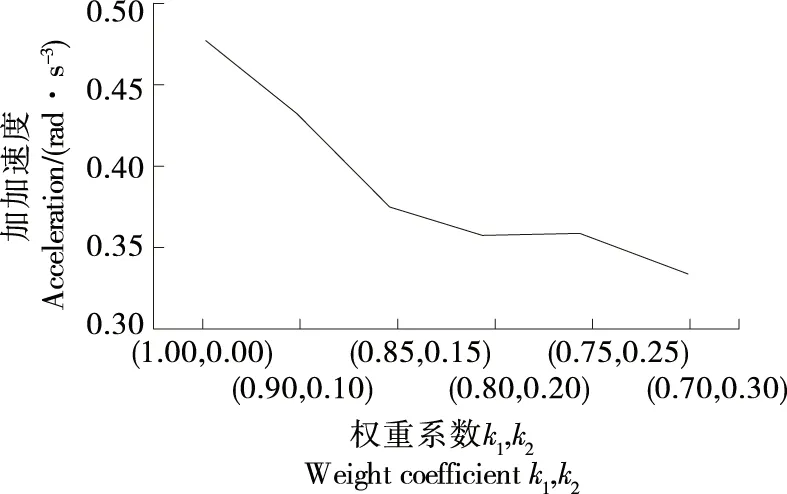
圖4 加加速度變化曲線Figure 4 Acceleration curve

從圖3和圖4可以看出，在不同權(quán)重系數(shù)下獲得的最優(yōu)解結(jié)果存在一定的偏差。在相同的仿真條件下，縮短運動時間和抑制振動的效果為對偶關(guān)系。如果運動周期的權(quán)重因子較高，則抑制振動的效果較弱。如果加加速度的權(quán)重因子較高，則平均作業(yè)時間會在一定程度上增加，這會降低高速并聯(lián)機器人拾放效率。因此，當對高速并聯(lián)機器人的作業(yè)周期要求較高，而對拾放穩(wěn)定性要求較低時，可以將k1值設(shè)置得較大；當高速并聯(lián)機器人拾放穩(wěn)定性要求較高且作業(yè)周期要求寬松時，可將k2值設(shè)置得較大。基于此，可以根據(jù)不同的操作要求靈活設(shè)定規(guī)劃目標以滿足不同的需求。

4 結(jié)論

基于高速并聯(lián)機器人的體系結(jié)構(gòu)，提出了一種運動軌跡規(guī)劃方法用于高速并聯(lián)機器人末端執(zhí)行器的軌跡優(yōu)化。建立多約束、多目標、非線性軌跡優(yōu)化模型，并通過改進的引力搜索算法求解。結(jié)果表明，與改進前的規(guī)劃方法相比，所提方法效率更高，能夠在較短的時間內(nèi)完成拾放任務(wù)，單次操作的最短時間為0.169 1 s。鑒于目前的試驗設(shè)備和數(shù)據(jù)規(guī)模，高速并聯(lián)機器人相關(guān)技術(shù)的研究尚處于起步階段，試驗僅研究了高速并聯(lián)機器人末端執(zhí)行器的運動軌跡規(guī)劃方法，未對其動力學和控制系統(tǒng)進行研究。在后期階段，應(yīng)不斷完善高速并聯(lián)機器人的相關(guān)功能，以適應(yīng)未來不斷變化的應(yīng)用環(huán)境。