一種改進的免疫算法研究

劉柏麟，吳湘華

摘要：傳統免疫算法是通過仿真免疫系統的多樣性機制設計出來的一種算法。傳統免疫算法在求解問題時候，算法存在收斂速度慢、容易陷入局部最優等問題。該文通過對傳統免疫算法中的變異函數和克隆抑制函數加以改進，以提高算法收斂速度，并使算法具有較好的全局最優性。通過測試函數驗證改進后的算法正確有效。

關鍵詞：免疫算法；變異函數；克隆抑制；收斂速度；全局最優

中圖分類號：G642? ? ? 文獻標識碼：A

文章編號：1009-3044（2022）32-0017-03

1 概述

自古以來，人類通過模擬生物體的結構、功能發明了很多技術和工具，來解決生活中的問題[1]。生物免疫系統作為一種復雜的系統，它能夠對外來的入侵物質進行自我識別和清除，同時它還具有自組織、分布式、自適應、動態均衡等性能。當外來的抗原侵入體內時，就會產生對應的抗體，其目的在于最大限度地確保機體的基本生理機能的正常運作，維持人體內部的穩定性。免疫算法基于生物免疫系統的免疫進化機理和信息處理機制，模擬其抗原識別和抗體增殖過程，保持抗體的多樣性[2]。傳統的免疫算法在局部最優問題上有待解決以及其收斂性也有待改進，為了優化這些問題，本文在傳統免疫算法的基礎上進行改進。

2 傳統免疫算法簡介

傳統免疫算法的原理是將抗體和抗原結合，進行抗體克隆、變異、選擇和記憶等過程，逐步達到抗體優化[3]。傳統免疫算法將待優化的問題的目標函數看成免疫系統中的抗原，算法中可行解看成免疫系統中的抗體，可行解的質量看成是抗體和抗原的親和度，通過進行抗體克隆、變異、選擇和記憶等操作，不斷優化抗體，利用抗體與抗原的親和性，確定目標函數和可行解之間的匹配度，確保可行解的差異性和多樣性，通過對抗體的期望生存率進行估計，以便促進較優抗體更好地進行遺傳和變異。選擇最佳的可行解作為記憶細胞，以避免出現相似的可行解，進而達到加快搜索全局最優解的目的。獨立的抗體種群進行選擇、克隆和變異等免疫操作[4]。在每次單獨群體的更新和評估之后，選擇不同種群的最優抗體進行多組評價，也就是目前群體中的最佳抗體與上一代的最優抗體相比較，若現有抗體較好，則將其作為本代的最佳抗體，反之，則將上一代的最佳抗體保存為該代的最佳抗體。最佳抗體就會被分配到各自的種群中，從而產生新的抗體。

免疫操作主要包括以下算子：

（1）免疫選擇：通過計算種群的抗體親和度，篩選出高質量的抗體，并進行活化；

（2）克隆：克隆經過選擇后的抗體，得到多個新的種群；

（3）變異：對克隆獲得的群體進行變異處理，從而產生突變；

（4）克隆抑制：對變異后的群體進行優選操作，保留親和度較高的抗體。

傳統免疫算法描述如下：

步驟1：參數的設定，在算法運行之前確定各個參數的取值。步驟2：初始化種群，根據設定的參數，隨機生成初始的抗體種群。步驟3：判定是否已達最大迭代代數，達到最大迭代代數則結束循環，并將執行步驟9；否則繼續執行步驟4。步驟4：抗原識別，根據問題構造相應的測試函數，染色體編碼代表抗體。步驟5：計算函數目標值，將種群中的抗體引入測試函數，得到相應的函數目標值，將其作為各抗體的親和度。步驟6：記憶單元的活化，向記憶單元內添加高親和度的抗體，并執行免疫操作。步驟7：執行免疫操作，主要執行的操作是選擇操作、克隆操作、變異操作和克隆抑制操作；選擇算子，即在群體中擇優，篩選更優的抗體以便于克隆；克隆算子是將選定的抗體復制到新的種群中；變異算子是指在克隆后所形成的種群中進行的突變；克隆抑制是指在變異后群體中重新篩選出具有較高親和力的抗體。步驟8：種群刷新，根據刷新比例從種群中隨機產生剩余個體，和上一步所保留的抗體刷新種群，并返回執行步驟3。步驟9：結束記憶細胞迭代，當達到指定的代數時，停止產生和選擇記憶細胞。

免疫算法是模仿生物免疫學和基因進化機理構造的優化搜索算法，是免疫計算的一種最重要形式和對生物免疫過程的一種數學仿真[4]。其主要特性如下：

（1）該算法模擬了免疫反應過程，是一種具有全局搜索功能的優化算法。其對高質量抗體局部搜索時通過變異算子和種群刷新來生成新的個體，并在一定范圍內尋找新的可能解區間，并保證了算法的全局收斂性。

（2）該算法采用了生物免疫系統中的多樣性維持機制，并根據抗體濃度的大小來判斷抗體的優劣。這種方法既能有效地抑制高濃度抗體，又能保證個體的多樣性，從而保證全局收斂。

（3）生物免疫系統可以隨時對抗原進行良好的識別[6]。該算法利用了啟發式的智能搜索機制，能夠在不受問題和初始值約束的情況下，從較差的解群體中尋找最優解，具有很好的魯棒性。

（4）該算法無需集中控制，能夠進行并行運算。此外，免疫算法的優化過程是一個多進程并行的過程。它能在尋找問題的最優解的過程中，獲得多個次最優解，即在尋找最優解的情況下，獲得了更好的選擇，特別適用于多模式優化問題。

（5）該算法在保持解的多樣性的同時，既采用了選擇、變異算子，又加入了隨機初始化群體，從而提高了解抗體的選擇能力，使算法能在全局最優條件下收斂。然而，與其他的智能算法相比，該算法在解決函數問題時，不能很好地收斂于全局最優，而且隨著時間的推移，其收斂速度和精確度也會逐步下降。

（6）該算法在優化多峰函數方面有較慢的收斂速度和精度較差的問題，通過簡單的提高抗體種群規模可以擴大免疫算法的搜索范圍，但是仍然會出現抗體退化、收斂速度慢的問題。

3 傳統免疫算法的改進

從免疫系統的角度出發，數值函數優化是在一定范圍內找到最佳值，相當于抗體種群進化來鑒別單個抗原。抗原與待解決的問題對應，最佳抗體與待解問題的最佳值對應，而函數值則與抗體與抗原的親和程度對應。本文對免疫變異算子克隆抑制算子進行改進。

3.1 免疫變異算子改進

在傳統的免疫算法中，大多數使用單點變異或者隨機取反來實現算法。本文定義變異點數量n，將算子從單點變異設置為多點變異，可以直觀地分析收斂速度隨著變異點數量n的改變有何變動，避免產生局部最優的問題，同時種群中的多樣性也得到提高。免疫變異算子im_mutation描述如下：

算子1：免疫變異算子im_mutation

功能：對克隆得到的種群進行n點隨機變異

輸入：克隆后形成的種群pop，變異點數量n

輸出：進行變異操作后形成的種群mupop

具體執行過程：

（1）設置變異點數量n；

（2）輸入克隆后得到的種群pop，令i = 1，j = 1；

（3）i <= px時執行（4），否則執行（7）；

（4）返回行向量index，包含從1到px沒有重復元素的整數隨機排列；

（5）j <= n時執行（6）且j值增1，否則i值增1返回（3）；

（6）將（4）中返回的元素作為序列，對每一個序列指定的變異點值進行取反運算；

（7）輸出進行變異后的形成的種群mupop。

3.2 克隆抑制算子改進

通常，克隆抑制算子是對變異后的種群進行則最優個體，進行種群刷新迭代。傳統免疫算法抑制后截取的個體數一般為常數，沒有充分研究該值對算法的影響，改進后的算法定義抑制后截取的個體數k，篩選出具有較高的親和度的k個抗體，親和度較低的抗體達到抑制效果。k取值過小不利于尋找全局最優解和收斂代數可能較大，k取值過大，每代運算時間會增加，影響收斂速度，克隆抑制算子k值的選取對收斂效果起到極其關鍵的作用，通過研究k值對算法效率的影響，以指導在實際問題中如何更好地進行克隆抑制操作。克隆抑制算子inhibit_clone描述如下：

算子2：克隆抑制算子inhibit_clone

功能：在經過變異后的種群中取出k個最優個體

輸入：變異后形成的種群pop，求解區間bounds，抑制后截取個體數k

輸出：個體進行克隆抑制操作后形成的種群newpop

具體執行過程：

（1）輸入變異后的二進制種群pop，求解區間bounds，抑制后截取個體數k；

（2）計算出群體中每條染色體個體的目標值objvalue；

（3）根據親和度大小排序，逆序；

（4）截取第1行到第k行作為新的二進制種群；

（5）輸出個體進行克隆抑制操作后的形成的種群newpop。

4 實驗仿真

4.1 算法的最優解截止代數判定

本文中免疫算法優化的評估標準是綜合考慮最優目標值、方差、熵值，體現實際免疫系統的多樣性[7]。方差表示種群在某個空間的分布情況，信息熵表示種群中個體的混亂程度。方差定義為：[D（X）=k=1，2，3...[X-E（X）]2pk]，其中[X]表示種群，[E（X）]表示種群均值，[pk]表示分布概率。熵值定義為：[H（X）=-k=1，2，3...p（xi）log2p（xi）]其中[p（xi）]表示個體在種群中的占比。當方差和熵值都比較大的時候，說明搜索空間大而且種群多樣性強，適合初始種群情況。如果種群的方差小、熵值大，說明搜索空間較小且種群的多樣性比較強。如果種群的方差大、熵值小，說明搜索空間較大且種群的多樣性較為弱。當熵值和方差都趨于一定的極小值時，群體中的最優個體占比最大，此時免疫算法無法找到更優解，即可判定收斂。

3.1 仿真參數設定

為了驗證算子改進后，免疫算法在求解函數中各種優化問題時的改進效果及優越性，選擇幾個常用測試函數進行仿真，下面以測試函數f（x） = x + 10× sin（5×x） + 7×cos（4×x），x∈[-10，10]，進行詳細的數據分析。種群大小設置為100，精度設置染色體長度為18，單次克隆個體數為10，種群刷新比例為0.3，進化代數設置為100代，變異點n取1～4，抑制操作后截取的個體數取1～4，本文設置了兩個變量對算法進行改進，變異點數量n和抑制后截取個體數k。對兩者進行單一變量分析，判斷算法收斂性能是否提升。

4.2 仿真結果分析

使用單一變量原則固定一個種群，變異點數量n和抑制后截取個體數k兩者選取一個作為變量，進行免疫算法操作，通過觀察最優目標值與最優值占比關系、方差和熵值關系，得出收斂代數。通過以上方法，對比多個不同種群的收斂代數，觀察變異點數量n和抑制后截取個體數k這兩個變量對算法收斂速度的影響。以下對初始種群pop1進行具體舉例。

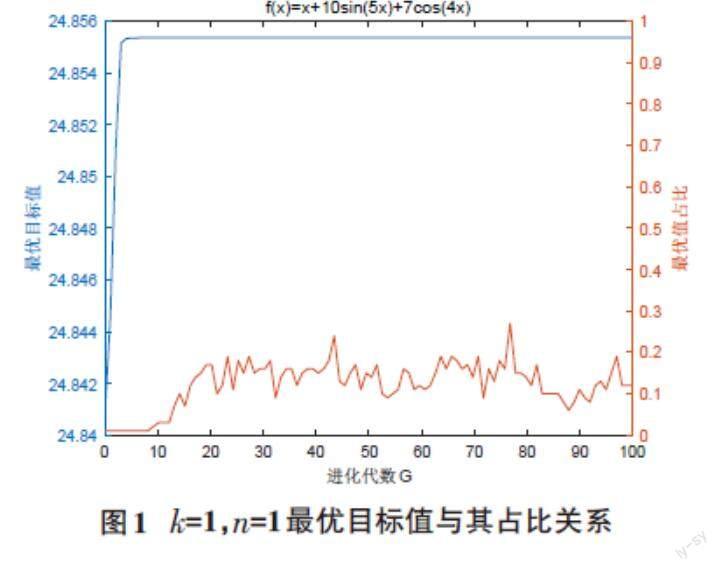
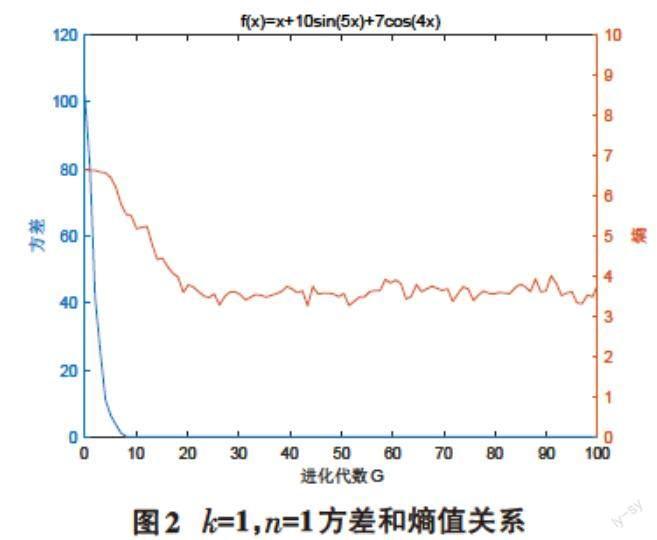
（1）當初始種群pop1和抑制后截取個體數k =1固定不變時，單一變量變異點數量n=1時，在進化代數G的變化下，最優目標值與其占比關系見圖1，方差和熵值關系見圖2。

由此可知，當抑制后截取個體數k=1，變異點數量n=1時，種群在44代時收斂。

同理，由此可知，當抑制后截取個體數k=1，變異點數量n=2時，種群在11代時收斂；當抑制后截取個體數k=1，變異點數量n=3時，種群在23代時收斂；當抑制后截取個體數k=1，變異點數量n=4時，種群在20代時收斂；當變異點數量n=3， 抑制后截取個體數k=2時，種群在12代時收斂；當變異點數量n=3， 抑制后截取個體數k=3時，種群在13代時收斂；當變異點數量n=3， 抑制后截取個體數k=4時，種群在8代時收斂。

以此類推，通過以上方法測試六組不同的種群，運用單一變量原則，觀察變異點數量n和克隆抑制后截取個體數k的改變對算法收斂性能的影響。

當k=1時，收斂代數如表1：

當n=3時，收斂代數如表2：

通過以上的仿真數據可知，固定始種群和變異點數量，抑制后截取個體數設置為變量；亦或固定初始種群和抑制后截取個體數，變異點數量設置為變量，可以明顯地觀察到算法收斂速度變化。當n值和k值過小時，都會使收斂性能下降。由此判斷，想要提高算法的收斂性能，可以在變量上選擇采用多點變異n和適當選取抑制后截取個體數k。

5 結論

免疫算法是一種以人工免疫系統為基礎的學習算法，它具有較強的自主性和應答性，同時還具備了一定的搜索和優化的能力。其基本思想是將抗體與抗原結合，經過抗體選擇、克隆、變異、記憶等步驟，使抗體得到最優。本文通過設置變異點數量與克隆抑制后截取個體數，對算法進行了改進和創新。

參考文獻：

[1] Mohammadi M，Raahemi B，Akbari A，et al.Improving linear discriminant analysis with artificial immune system-based evolutionary algorithms[J].Information Sciences，2012，189：219-232.

[2] 張曉.人工免疫算法改進及其應用研究[D].西安：陜西師范大學，2017.

[3] 馬春連.基于人工免疫系統的多目標進化算法的研究[D].淮南：安徽理工大學，2014.

[4] 汪桂金，胡劍鋒.多種群人工免疫算法在多峰函數上的優化[J].南昌大學學報（工科版），2018，40（3）：299-302，306.

[5] 蔡自興，龔濤.免疫算法研究的進展[J].控制與決策，2004，19（8）：841-846.

[6] 石剛.改進免疫克隆選擇算法的研究與應用[D].沈陽：東北大學，2011.

[7] 孫寧.人工免疫優化算法及其應用研究[D].哈爾濱：哈爾濱工業大學，2006.

【通聯編輯：朱寶貴】