低/高速飛行器系統編隊協同控制方法研究進展

安凱 郭振云 黃偉 徐小平

摘 要： 編隊控制作為一種多飛行器系統典型的協同控制方式，可以有效解決單個飛行器在信息獲取、區域探測、綜合打擊等方面的不足。本文總結了低速和高速兩類飛行器系統編隊控制方法的研究進展。首先介紹了領隊-跟隨控制法、虛擬結構法、行為控制法及一致性編隊控制法四種主流編隊控制策略的基本概念，分析了各自的結構特點和策略優勢。隨后，結合這四種方法，總結了無人機和低速導彈兩類低速多飛行器系統的控制特點和性能差異。特殊的飛行特性使得高速飛行器編隊控制對系統響應的容錯性、快速性和精準性要求更高。然后， 對高速飛行器編隊控制的理論實踐和應用探索過程進行了梳理，提出仍需克服的應用難題。最后， 對飛行器編隊控制的發展趨勢進行展望，為未來開展多飛行器系統編隊控制理論和應用研究提供參考。

關鍵詞：集群智能；協同控制； 虛擬結構；行為控制；編隊控制；飛行器

中圖分類號：TJ760；V249.1

文獻標識碼：A

文章編號：1673-5048（2022）05-0053-13

DOI：10.12132/ISSN.1673-5048.2022.0067

0 引? 言

信息技術和人工智能技術的發展，促使新型集群智能研究領域的誕生。在航空航天和軍事領域，集群智能已然體現出巨大的技術優勢，成為各國爭奪的技術制高點。自2000年美國第一屆協同控制和優化研討會上定義了協同系統以來［1］，多飛行器系統協同控制技術得到了巨大的發展，表現出強大的集群優勢。如無人機集群系統持續作戰能力強，生存能力較單個飛行器有了極大提高，且成本低，體系靈活性強；導彈集群提升了對單個或多個目標的綜合打擊能力；航天器的集群化部署可以增強空間生存和打擊能力，不僅擴大了信息獲取范圍，而且縮短了復雜空間科學任務的完成周期，是地-空-天聯合體系的重要平臺。上述多飛行器系統相比單個主體執行任務所表現出的諸多優勢，使其受到越來越多的關注和重視，而且越來越多的任務也將以群體智能協同的方式進行分布式決策執行。多飛行器編隊控制作為實現多飛行器系統應用層面的關鍵技術之一，已然成為協同控制領域的研究熱點，獲得了廣泛的研究和探索。

編隊控制的概念主要來源于對自然界生物群體的行為研究。編隊控制通常是指多個飛行器在執行任務過程中，形成并保持滿足性能指標、飛行約束、任務目標等要求的幾何構型。因此， 編隊控制實際上是對飛行器編隊隊形的控制研究。隊形控制主要解決兩個問題：一是編隊隊形的構成、保持與重構策略。不同任務場景下需要設計不同的編隊控制策略，以實現隊形不同狀態的變換，包括飛行時的編隊生成、正常飛行狀態下的編隊保持、飛行路徑遇到障礙時編隊的拆分和重建，以及飛行器離隊和入隊后的編隊重構等。二是編隊控制器的設計。在有效控制策略的基礎上，核心是設計編隊控制器。控制器不僅需要關心各個飛行器的飛行狀態，還需要協調控制互相之間的各類約束要求，包括編隊控制的位置、速度、姿態以及信息傳遞等［2］。因此，多飛行器系統編隊控制方法包括隊形策略和控制器兩方面的研究。

當前應用于不同多飛行器系統的編隊控制方法雖然各異，但相互之間又具有很強的相關性，可以互相借鑒進而拓展應用。多飛行器編隊控制方法的研究多是針對無人機和低速導彈等低速飛行器系統展開， 產生豐碩的研究成果［3-5］，而高速飛行器由于其飛行速度快、飛行空域多變、速度變化劇烈等因素，其編隊控制本身充滿

了挑戰性，目前還停留在探索研究階段，難以工程應用。近十年來雖然有很多學者根據飛行特性對高速飛行器的協同控制技術開展了大量研究，但是關于其編隊控制問題的研究卻較少。

1 主流編隊控制策略

編隊控制策略最先是從地面機器人的協同控制問題開始研究的。Wang［6］從機器人編隊的導航策略入手，研究了幾種簡單的編隊控制方法，包括單個鄰近點跟蹤控制（跟隨領隊的參考狀態）、多個鄰近點跟蹤控制、基于慣性參考狀態的跟蹤控制以及鄰近點跟蹤與慣性狀態跟蹤相結合等方法。在這四種方法中，前兩種很接近于領隊-跟隨控制法，第三種與行為控制法類似，后續開展的編隊控制策略研究也基本上都以此為基礎進行拓展。因此，根據不同任務場景、約束條件以及目標要求進行分類，飛行器系統編隊控制策略主要劃分為：領隊-跟隨控制法、虛擬結構控制法、行為控制法以及一致性編隊控制法。

1.1 領隊-跟隨控制法

領隊-跟隨控制法是目前研究成果最多、發展最成熟的一種編隊控制方法。其基本思想是，首先指定多飛行器系統中的一個或多個個體為領隊，其余飛行器為跟隨個體，然后對領隊個體的行為狀態設計期望值，跟隨個體設計控制器跟蹤領隊個體的參考狀態并保持一定的空間和角度位置，避免碰撞和發生沖突，從而實現整體的一致性。

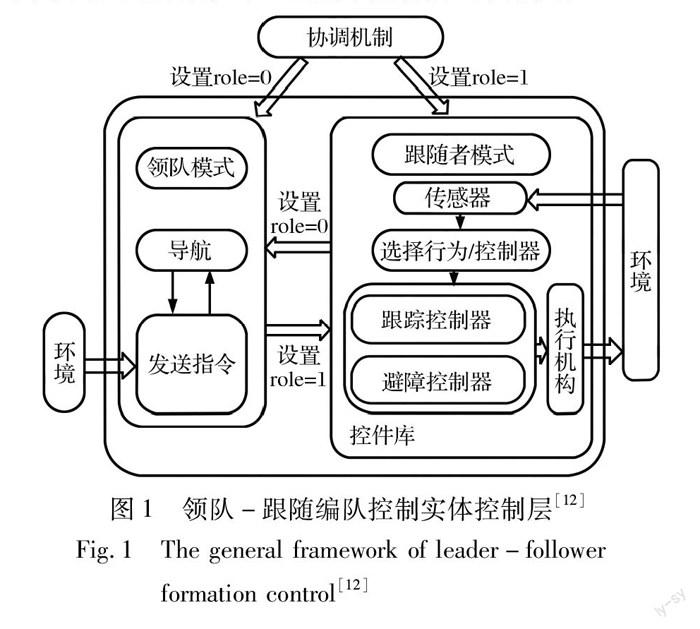
領隊-跟隨控制法最先是從機器人的協同控制研究中開始獲得關注的［7-9］。Beard等［10］發展了一種通用的領-從協調結構，設定領隊為集中協調控制單元，跟隨體為接收單元和反饋單元，通過領隊收集、處理跟隨體的狀態信息，然后傳遞給跟隨體，跟隨體將自身執行后的狀態變量再反饋回領隊形成閉環。另外，該方法規定如果領隊失效，則其他個體可獲得領隊信息的復制，從而繼承領隊功能。Edwards等［11］也設定領隊僅能通過廣播的形式與跟隨體進行信息交流，使跟隨體獲取相對位置、速度等狀態進行狀態/軌跡跟蹤。如果領隊失效，則跟隨體可重新選擇領隊或者以各自的導航信息單獨完成任務。另外，討論了編隊隊形在一維、二維和三維空間的重構問題，并通過實驗進行了驗證，因而相比之下更具有實踐意義。Shao等［12］進一步發展了一種通用的領-從編隊控制算法框架，如圖1所示。該框架包含三層混合結構。第一層稱為協調層，選定一個機器人為領隊，負責設計得到一條可以到達目標的合適軌跡；第二層為領-從控制層，負責構建形成以2個機器人為組合對的領-從子系統；第三層是實體控制層，為領隊模式和跟隨者模式，當領隊存在時，采用第一種模式，否則執行第二種模式。跟隨層級將個體信息傳遞至領隊層級，領隊層級綜合處理后向跟隨層級發送指令，跟隨個體在傳感器和控制器作用下進行跟蹤控制和避障控制。該方法考慮了系統的通信要求，僅通過鄰近個體進行信息傳遞，是一種有效的編隊控制策略。另外，該框架為領隊失效做了簡單的應對方案，可以通過跟隨者模式來解決。

文獻［13］討論了兩種編隊形式：線形編隊和樹狀編隊，并發展了編隊模擬器進行模擬驗證，其中包含模型模塊、傳感器模塊、避碰模塊、通信模塊等，同時采用遺傳算法進行整體優化，相比之下控制指標可以取得更優的結果。文獻［14］也在類似的領-從框架中考慮了避碰問題，采用位置傳感器進行預警，同時應用優化方法來尋求最優的控制結果。

文獻［15］給出了四種常見的編隊形式，包括行形、線形、V形和鉆石形，如圖2所示。其中，領隊均被放置到隊形首位，在編隊形式上是典型的領-從結構。但是這種編隊控制形式存在兩個典型問題：一是領隊容易受到攻擊；二是領隊出現故障后對其他跟隨體會產生較大的影響。因此在實際應用中，應盡量選擇一個安全性和影響性綜合最優的位置。

綜上，按照控制形式可以將領隊-跟隨控制法分為兩種：第一種是所有跟隨者只有一個領隊；第二種是跟隨者跟隨鄰近指定的領隊。按照隊形設置分為三類：第一類是將領隊和跟隨者看作質點，保持一定的相對距離，跟隨者只跟蹤領隊的參考軌跡；第二類是跟隨者不僅要和領隊保持距離關系，還要保持一定的角度關系，就可以形成更復雜的編隊；第三類是前兩種形式的混合應用。

領隊-跟隨控制法本質上是一種集中式協同控制方法，即所有跟隨體都需要參考領隊的狀態進行狀態跟蹤和信息交換，雖然簡化了集群系統的整體控制方式，但是當系統受到擾動或者領隊失效時，系統魯棒性較差，編隊可能無法維持，同時整個控制結構不能處理跟隨體故障或失效的情況。領隊-跟隨控制法的策略是通過設置領隊和跟隨體來構建編隊形式，從而形成和保持編隊隊形，但實際應用中該方法并不單獨使用，一般多與其他控制算法結合進行飛行器編隊的綜合控制。

1.2 虛擬結構控制法

虛擬結構控制法與領隊-跟隨控制法類似，都需要維持一定的隊形。不同點在于，該方法中的飛行器系統被視為一個剛性結構或者其他形式的虛擬結構，所有飛行器跟隨剛性或虛擬結構上各自對應的虛構的點運動。Tan等［16-17］給出了上述虛擬結構的定義，指出通過反饋并最小化每個飛行器相對于虛擬結構點的位置誤差即可實現編隊控制，但只給出了固定虛擬結構下的控制策略，對可變虛擬結構以及分層虛擬結構控制進行展望，指出虛擬結構控制法不依賴于隊形形狀，任意隊形都可實現編隊控制。另外，由于提出的虛擬結構法沒有領-從之分，可以對編隊中的故障個體進行容錯，即單個或多個個體的失效不會影響其他個體跟蹤虛擬控制點的運動，基于此特性，該方法可實現分布式編隊控制。相比于領-從結構，算法的優勢非常明顯。

除上述虛擬控制策略，Leonard等［18］將領-從編隊思路和虛擬結構控制策略相結合發展了一種虛擬領隊結構下的編隊協調控制框架，具體編隊模式如圖3所示。該框架中，虛擬領隊是一個移動的參考點，并通過附加的人工勢場影響附近的個體。虛擬領隊可直接影響和控制編隊的幾何形狀，引導編隊的運動。另外，文獻進一步對三維空間的編隊協調控制以及基于虛擬領隊結構的編隊避障、隊形劃分等提出展望。

文獻［19］以交互方式提出了一種雙向控制方案，即飛行器由施加在虛擬結構上的虛擬力控制，該虛擬力可以是重力，也可以是人工勢場力，而虛擬結構的位置由整個編隊的平均位置決定，如圖4所示。在該方案中，具體的控制策略分為三個步驟： （1）由于與虛擬結構存在位置誤差，首先對飛行器預定義位置映射，確定點對點跟蹤狀態（如圖4（a））； （2）調整虛擬結構到最佳位置，然后通過虛擬力計算下一時刻的位移（如圖4（b））； （3）飛行器精確跟蹤各自的相對位置參考點完成編隊飛行（如圖4（c））。

虛擬結構控制法較領隊-跟隨控制法簡化了任務分配和描述，具有較高的編隊控制精度，容錯能力提升，單個個體的失效也會被整個編隊感知，可以通過其他隊形變換機制調整隊形。但是虛擬點的選取具有單一性和復雜性，因而當前對于該方法的應用研究較少。

同樣，在對不同對象的實際應用中，虛擬結構控制法通常根據實際場景結合其他算法進行綜合控制。一般將整個編隊視為剛體結構后，虛擬結構可以看作是帶有動力學模型的質點或其他模型（如非線性動力學模型、具有氣動力和力矩的實體對象等），然后根據相應理論（如PID控制、動態逆控制、模型預測控制法、模糊推理等）對整個剛體結構以及個體進行控制器設計［20-22］。

1.3 行為控制法

行為控制法由Balch等［23］在1998年首次提出，給出了四種簡單行為控制模式：向目標移動、規避靜態障礙、規避動態障礙以及保持編隊形式。其中，每種模式生成一個矢量代表期望的行為響應（運動方向和幅度），采用權重值表示個體行為中每種行為的相對重要程度，然后將基本行為模式的輸出與權重的乘積再求和并規范化，得到高級組合形式下的行為模式。

因此，行為控制法的思想可以描述為：通過設定多飛行器系統的行為機制，如一般的保持編隊、避障飛行、隊形變換、目標偵察等，當飛行器遇到對應的情況時根據行為機制判斷自身需要采取的策略，然后根據評價方案或評價指標最終實現整體的行為協調，主要調整位置、速度以及角度三個狀態量。

Song等［24］提出了基于四種基本行為模式和權重法的加權平均行為選擇機制，但與文獻［23］不同的是，文中將隨機行為作為一種基本行為模式進行考慮。而Xu等［25］針對初始編隊形成和編隊避障控制兩個問題設計了五種行為模式，并討論了將行為控制法應用到未知環境避障的問題，如圖5所示。這五種行為模式比較簡單，在復雜環境下可能會存在行為判斷錯誤，例如將墻壁視為障礙進行規避。

文獻［26-27］同樣采用基本模式來構建復雜網絡系統，借鑒了面向對象的思想，構建了基于行為的一體化控制結構。該結構是由封裝五種基本行為的模塊構成，通過模塊之間輸入輸出的相互作用實現復雜的功能。該結構模塊集成化程度更高，但缺點也非常突出，當智能體執行更多、更復雜的功能時，結構復雜性和系統計算量會隨著集成模塊的增多而指數增長，這對于故障檢測和誤差分析將造成極大困難。Lee等［28］借鑒文獻［26-27］中的模塊化思想，提出一種基于行為控制策略的分布式編隊控制結構，減小了系統復雜度。該結構分為三層，即編隊生成層、避障層和個體位置控制層，并實現兩個控制目標：生成避障軌跡和保持編隊形狀。根據個體與障礙位置關系確定規避角度來生成避障軌跡，同時在系統中選擇領隊，并確定編隊矩陣來保持編隊形狀。

綜上可知，行為控制法可以認為是智能性的一種體現，但是由于行為模式庫規則設置簡單，集群系統中個體可執行的操作是非常有限的，因此智能性表現較低。如果行為模式規則考慮的一般情況和特殊情況豐富，能夠涵蓋許多復雜的應用場景，能夠充分考慮不同情況條件下的行為執行分支，雖然能大幅提高系統智能性，但在加權行為選擇機制的排列組合下，整個系統需要設定的邏輯規則將會非常繁瑣，導致計算量大幅遞增，集群系統的執行過程也會更容易產生邏輯錯誤，因此，如何設計并找到復雜度和計算量的平衡是非常重要的。可以采用優化的策略來進行分配。

基于行為的編隊控制法同樣具有一定優勢。其是一種分布式的控制結構，系統可以實時反饋，動態變換隊形，伸縮性較好，因而相較前兩種方法，避障機制是很容易考慮的。缺點在于對系統進行數學分析和穩定性證明困難，如果應用到復雜性和非線性更高的數學模型，可能無法給出完整的證明結論。

1.4 一致性編隊控制法

不同于上述三種對編隊隊形結構形式分析的方法，多智能體一致性算法將重點放在了系統的一致性和通信拓撲結構研究中（如時間一致性、速度一致性、通信時延等），為編隊控制算法帶來巨大算法優勢和應用潛力。一致性編隊控制法對編隊隊形沒有直接要求，也不對隊形進行直接控制，而是基于圖論構建通信拓撲鏈式結構，只需要給定智能體之間的通信協議，規定通信信息流，再設計一致性控制算法就可實現分布式編隊控制。

首先，必須證明一致性理論的收斂性和穩定性。Tsitsiklis等［29］在20世紀80年代最早提出一致性控制理論，并應用到分布式決策問題的求解當中。由于其證明過程簡捷，算法收斂效果很好，隨后得到大量學者的研究。Lin［30］，Olfati-Saber［31］，Jadbabaie［32］等對一階系統的一致性問題進行研究，給出一階系統一致性問題的通用定義，并提出一種線性的一致性算法。Moreau［33］在一階系統一致性理論發展的基礎上運用李雅普諾夫方法和凸性理論，解決了離散多智能體系統的一致性問題。Ren等［34］同時研究了離散和連續兩種多智能體系統一致性的基本問題，證明當多智能體系統的通信拓撲結構中含有一個有向生成樹時，該系統能達到一致性。基于無向圖的二階系統的一致性問題［35-37］進一步發展了一致性理論。上述研究極大推動了一致性理論的發展，使之在協同控制領域占據了重要地位。

Ren［38］后續又針對二階動力學系統提出基于一致性的編隊控制策略，在考慮僅有鄰近個體交換信息的條件下，為保證編隊控制的精確性，擴展了一階一致性算法，并指出領隊-跟隨控制法、虛擬結構控制法和行為控制法都能統一到通用的一致性框架中。這種統一的好處在于，一致性框架只需要局部鄰近個體之間的信息交換，并任意信息流引入反饋或是耦合行為，從而提高整個系統的冗余度和魯棒性，而不會使控制律設計和收斂/穩定性分析復雜化。文獻［39］研究了剛性圖控制結構下編隊的合并、拆分及閉合，區分剛性圖結構下剛體編隊形式和非剛體編隊形式，并給出全局剛性圖結構的充要條件，當一個剛性圖結構中包含附加的距離約束時，該剛性圖結構可以轉換為全局剛性圖結構。此外，文獻還討論了如圖6所示的編隊拆分及閉合的過程。遇到障礙時，根據算法進行編隊拆分，形成多個編組，完成繞飛后再組成新的編隊結構。當編隊結構中一個或多個個體失效或出隊、入隊時，閉合指令可以對被破壞的圖結構進行修復或者重新進行聯接形成新的剛體圖結構。 上述結論解

決了一致性理論的可行性驗證和穩定性分析問題， 目的是為了構建通用的分布式協同控制框架，使之獲得廣泛應用。

此外，在一致性理論研究中，與通信拓撲相關的時延問題和拓撲結構變換也是非常關鍵的問題，一般圍繞通信穩定性、魯棒性等要求開展，目的是設計有效的拓撲結構從而實現編隊控制狀態的一致性［40-42］。Fax等［43］研究了固定時延約束下的線性系統，并針對代數圖論在通信網絡建模準則及其拓撲結構與編隊穩定性的關系進行了穩定性證明。奈奎斯特準則應用圖的拉普拉斯矩陣的特征值來判斷通信拓撲結構對編隊穩定性的影響。同時，也證明了分離原理，該原理將編隊穩定性分解為給定圖結構中信息流的穩定性以及給定控制器下系統中每個個體的穩定性。該奈奎斯特準則和分離原理對一致性理論在集群系統協同控制算法設計和穩定性證明中起到非常重要的作用。文獻［44］研究了固定拓撲和時變拓撲條件下非線性系統的交互有限時間一致性問題，并設計了通用的控制算法。此外，對于編隊控制中的擾動問題，一致性理論也常用于干擾觀測器的設計，通過主動補償擾動項實現抗干擾［45-46］。

一致性理論在發展過程中逐漸與領隊-跟隨控制法、虛擬結構控制法和行為控制法等進行組合應用，通過其他三種方法構建編隊隊形，采用一致性理論設計控制算法，從而實現綜合控制。文獻［47］提出兩種基于行為控制方法的一致性策略，一是使用速度反饋，二是使用無源控制中的阻尼項。Jose等［48］基于代數圖論、矩陣論和控制論框架，討論了離散時間和連續時間下領隊-跟隨策略的一致性和協作性問題。Yoshioka［49］基于虛擬結構控制法構建了多智能體系統，設計控制律，分別實現了多智能體虛擬結構一致性、虛擬結構下的群集以及虛擬結構群集避障三個問題。Ji等［50］在領隊-跟隨控制結構中加入一致性策略，證明了集群系統的可控性可以由圖的拓撲結構唯一確定，并給出可控圖結構和不可控圖結構的充要條件。文獻［51］將高階一致性系統和領-從結構結合起來研究了編隊的時變跟蹤問題，并得到需要具備的可行性前提條件。

通過分析，基于一致性理論的編隊控制算法能夠在克服其他三種方法缺陷的基礎上，與其他算法相互組合形成魯棒性和穩定性更強的復合控制算法。同時，一致性理論的應用很大程度上簡化了編隊控制的協調困難問題，增強了編隊系統的自適應容錯性。

飛行器是一種控制復雜度較高的非線性模型，相比二維平面機器人的集群編隊控制來說難度更大，不單單需要位置、速度等狀態的反饋，還要考慮結構、穩定性、不確定性等更多的影響因素。當前無人機和導彈兩類低速飛行器系統基于四種主流編隊控制方法所開展的研究具有豐富的理論成果，而高速飛行器的編隊控制問題正處于研究起步階段，相關研究較少，相反，一些其他的典型協同控制方法在高速多飛行器系統上的應用相對較多。針對不同飛行器數學模型的差異和任務背景，許多學者在上述四種編隊控制框架的基礎上做出了不同的編隊隊形控制改進，然后結合其他控制或優化算法設計編隊控制器實現控制目標，控制表達式逐漸趨于復雜化和一般化，控制精度也逐漸提高。

2 低速飛行器系統編隊控制方法研究進展

2.1 無人機系統編隊控制方法研究進展

無人機編隊常應用于協同探測、協同監視、態勢感知、搜索營救與協同打擊等場景。發展無人機編隊控制技術可以提高無人機執行任務的效率，增強應對復雜環境任務需求的能力。

四種編隊控制方法中，領-從編隊控制法的應用尤其廣泛。Liu等［52］基于傳統領-從編隊結構，討論了平面內三個無人機的編隊容錯控制問題。通過角度和位置信息設計了外環控制器和內環控制器來處理編隊控制中存在的碰撞和執行器故障問題。其中，外環控制器采用PI控制器來保證編隊隊形結構和軌跡跟蹤性能，內環控制器采用自適應容錯控制方案和碰撞規避策略。容錯控制器保證了編隊始終穩定，同時規避障礙后仍能以期望的編隊飛行。Yu等［53］以三維場景領-從編隊梯隊隊形為背景，在理想動力學條件下提出一種分布式自適應容錯控制方案。該方案綜合應用了分布式滑模估計器、動態面控制結構、神經網絡和擾動觀測器等技術進行編隊控制器的設計，較文獻［52］具有更好的一般性；同時，方案采用的控制技術具有更好的擾動估計和控制精度。Chen等［54］將領隊-跟隨編隊結構拓展應用至大規模復雜化任務中，提出基于組的分層控制思想，如圖7所示。每個組自上而下構成領-從結構編隊單元，由李雅普諾夫理論設計跟蹤控制器，其中，領隊跟蹤虛擬目標的狀態，跟隨體跟蹤組內領隊的狀態，從而實現整體的編隊控制。另一方面，每個編隊單元具備獨立進行隊形變換和避障的能力，因此，將復雜任務分割成子任務后再獨立分配至各層，最后進行綜合分析。

在一致性控制算法的應用研究中，基于圖論開展編隊控制協議和通信拓撲結構理論化的數學推導和證明是主要的突破方向。其中，編隊控制協議目標是使編隊中各飛行器實現狀態一致性（使得位置或速度收斂并保持一致性變化），而通信拓撲結構是實現一致性的基礎，用于確定無人機之間的通信規則（如通信方向、通信分布等）并保證可靠性。

朱旭等［55］構建無人機等邊三角形的編隊隊形，并基于圖論建立通信拓撲協議規定無人機可兩兩之間通信，提出基于信息一致性的三段式編隊集結控制策略，包括選取參考集結點、分配目標集結點、形成松散編隊和緊密編隊。其中，形成松散編隊時只需要保證速度一致性，而形成緊密編隊時需要保證速度、位置以及姿態的一致性，最終實現編隊航跡控制。文獻采用了通用的二階一致性控制算法與PID控制算法結合，重點是對編隊集結策略的實現。Dong等［56-58］將一致性理論應用于解決無人機系統的時變編隊控制問題，重點研究了通信拓撲結構的切換。其中，文獻［56］設計了一種時變編隊拓撲算法，給出了實現時變編隊的充要條件并進行了證明，能夠實現預置的時變編隊形式。以5架無人機為例，規定信息傳遞方向為順時針方向，開展了仿真驗證和試驗驗證。文獻［57］在時變編隊拓撲算法的基礎上，進一步提出采用切換通信拓撲的方式實現編隊一致性，通信拓撲方式包含四種，時間間隔10 s切換一次。文獻［58］在上述研究的基礎上結合領-從結構，提出具有定向和切換交互拓撲的時變編隊跟蹤控制問題。設計的控制器內環控制無人機姿態，外環控制位置和速度，同時利用局部鄰域信息構造了一個時變編隊跟蹤控制協議，分別以4架無人機和11架無人機開展了仿真和試驗驗證，取得了良好的編隊控制效果。文獻［59］基于一致性理論和無向圖結構設計了分布式編隊算法，并給出了詳細的穩定性和收斂性證明。基于一致性理論設計的編隊控制算法克服了其他控制方式下需要設計復雜策略的缺陷，能夠將復雜的編隊隊形控制及編隊運動解析式化，大幅提高了算法的通用性。但難點在于設計的一致性算法必須進行證明收斂性和穩定性后才能應用，需要具備較強的數理推理能力。此外，越來越多的研究開始將領-從結構與一致性理論相互結合應用，逐漸形成了兩者相互耦合的系統框架。

對于虛擬結構法的應用，Askari等［20］在構建虛擬圓環結構的基礎上將編隊反饋和動態逆控制相結合，構建了一個新的編隊控制結構框架，采用內外環PID控制器/動態逆控制方法設計，實現了姿態角和速度的一致性控制。優勢在于該結構的可行性和控制精度通過無人機六自由度仿真環境進行了驗證，并且能推廣到更多無人機個體的編隊控制中，缺陷在于沒有考慮避碰和時延問題。He等［60］同樣構建了虛擬圓環結構作為編隊策略，提出采用狀態輸出反饋方式來對路徑參數進行校正和更新，設計了一種分布式的輸出反饋編隊控制律。將虛擬點的運動軌跡作為參考軌跡，各無人機對參考狀態進行跟蹤，但算法僅在二維平面內得到驗證，而且也沒有考慮避碰和時延問題。Zhang等［61］采用虛擬領隊結構法設計了三維空間內的編隊避障控制算法，采用人工勢場法為目標和障礙構建勢場域，其中，目標為引力勢場，障礙物為斥力勢場，從而對避障問題提供了求解思路。可以看出，虛擬結構作為編隊策略能夠克服領-從結構下領隊失效的問題，以便后續個體控制律的設計，提升系統魯棒性，但虛擬結構法中避障策略和時延問題的引入， 可能無法保證編隊控制精度，同時也限制了編隊更復雜行為的設計。

對于行為控制法，一方面如果行為模式規則設置比較簡單，則無人機群無法完成復雜化的任務；而另一方面如果行為模式庫設置復雜，則計算時間就會大幅增加，系統容錯率也更低。因此，行為控制法一般應用于地面機器人的編隊控制中，而飛行器等應用較少。

除了四種主流編隊控制策略結合一般控制器設計進行應用外，優化算法、反饋線性化控制、滑模控制、模型預測控制等方法也常應用于編隊控制器的設計，這些理論和方法相比之下能夠更加靈活地處理避障、約束、不確定性等復雜問題，得到最優或次優的控制結果。Kim等［62］采用反饋線性化方法提出一種基于無人機行為的編隊分散飛行方法，同時采用優化方法對每個無人機行為的相對權重進行優化，得到了最優的控制參數。Wang等［63］考慮二維平面內無人機環形編隊飛行規避固定障礙的任務場景，給出一種雙向模式控制策略——“安全模式”和“危險模式”。在“安全模式”下，實現無人機的編隊飛行軌跡優化，生成最優或次優軌跡；在“危險模式”下，提出了一種基于改進Grossberg神經網絡（GNN）的障礙物/碰撞規避算法，最后應用模型預測跟蹤控制方法跟蹤參考軌跡并處理約束。文獻［64-66］討論了模型預測控制方法在無人機編隊控制中的應用，模型預測控制相比優化算法雖然不能滿足最優化條件，但是其建模方便，過程采用滾動優化策略和反饋控制來克服不確定性、非線性、各種約束等，具有控制效果好、魯棒性強等優勢。文獻［67-68］采用高階滑模控制算法（如二階超螺旋滑模控制算法）設計了一致性編隊控制協議，實現了領-從結構下無碰撞路徑的跟蹤編隊控制，得到了相比傳統滑模控制算法下誤差更小的結果。Han等［69］對每個無人機設置了三種行為規則，利用人工勢能函數對群集編隊過程進行建模，同時，采用滑模控制算法來抑制可變系統的不確定性，凸顯出滑模理論在處理擾動因素方面的優勢。Wang等［70］討論三維空間內四邊形編隊場景，控制無人機編隊飛行至目標區域。將無人機的編隊控制、軌跡跟蹤以及避障控制集成到一個統一的最優控制框架中，以無人機位置和速度作為控制變量，通過逆最優控制方法構造一個避障價值函數，求得解析解形式的最優控制律，保證了編隊系統不僅可以完成對期望軌跡的跟蹤，也可以實現對固定障礙的規避，飛行場景示意圖如圖8所示，3號飛行器避障后重新與其他飛行器編隊形成新的隊形。

文獻［71］將一致性理論和傳統滑模控制方法結合，設計了分布式滑模控制算法，并在仿真中驗證了控制算法的優勢。為提高無人機編隊的智能性，有學者提出基于遞歸神經網絡（RNNs）的智能領隊-跟隨一致性形成控制方法，利用RNN在線學習系統的不確定性來改善編隊控制的自適應性［72］。

綜上，由于無人機模型非線性程度低、飛行速度小、可控性強、靈活度高，編隊控制的研究重點在于其控制協議的設計和新理論的創新應用。四種主流的編隊控制策略或是嵌入到以一致性理論為基礎的控制框架中，或是與其他先進的控制理論相互結合發揮策略優勢，凸顯應用價值，因此，復合編隊控制成為主要應用特點。相反，目前研究的盲區和缺陷主要在于不確定性問題的考慮，當前大部分研究均是基于理想控制狀態的。同時，大部分研究均停留在仿真驗證階段，實踐化和工程化是設計策略和算法的最終目的，尤其對于無人機這類實現困難小、應用難度低的飛行器，應促進技術的快速轉化。

2.2 低速導彈系統編隊控制方法研究進展

導彈與無人機系統存在很大不同（如飛行特性、任務背景等）。首先，導彈系統的協同更具有目的性和攻擊性。導彈由于其快速性，需要在較短的時間內精確導引至目標，實現精準打擊。作戰場景中，目標類型分為固定目標和移動目標兩類，在導彈進入末制導區域范圍之前，系統的編隊控制可以參考無人機的編隊策略，包括避障、保持編隊形式等，而進入末制導區域后，需要著重考慮導彈各自到達目標的攻擊時間和末端攻擊角度來實現協同/飽和攻擊，從而大大提高導彈編隊系統的命中概率。其次，導彈編隊系統中個體之間的相對距離要遠大于無人機編隊，使得信息傳遞問題更加嚴峻。另外，導彈系統中不確定性因素是非常重要的，包括模型不確定性、參數不確定性、環境不確定性以及外部隨機/規則擾動（運動目標的速度/軌跡）等，因此，編隊控制方法要考慮更多復雜性。本文所述的低速導彈定義為馬赫數小于3的導彈類型。

導彈按軌跡特征通常分為爬升段、中段（巡航段）及末制導段，其中，中段飛行高度、速度等均較穩定，因而在該飛行階段能夠保證編隊穩定飛行。此外，在仿真驗證中也是直接以中段飛行參數作為初始條件進行計算。

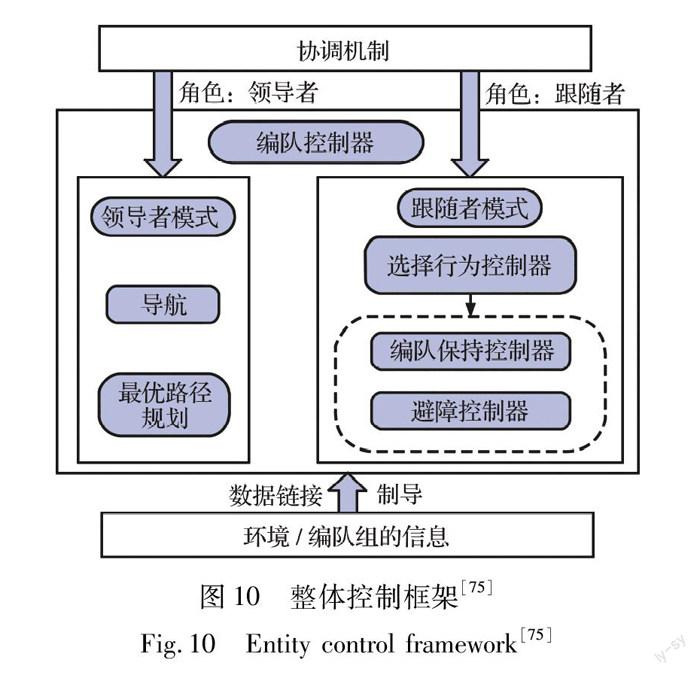
Cui等［73］以三維空間三角形領-從編隊結構發展了一種基于總能量控制理論的BTT導彈智能自動駕駛儀，如圖9所示。領隊將自身期望狀態傳遞給跟隨導彈的控制系統，然后控制系統根據位置偏差和期望狀態計算得到跟隨導彈的期望狀態。其中，單枚導彈的控制指令采用位置誤差的PD控制器生成，總能量控制理論用于導彈外環控制器的設計，內環控制器采用傳統的過載控制器。由于是三通道獨立控制，在每個通道都具有良好的軌跡跟蹤性能，跟蹤誤差小且響應速度快。Wei等［74］進一步考慮領隊失效的問題，也通過設計自適應PD控制器來保持領-從編隊結構的穩定性，不同的是采用全狀態反饋進行控制，提高了系統容錯能力。另外，由于自適應律的存在，該算法在遇到領隊失效而切換控制器時，會發生明顯的抖振問題，使得系統狀態發生突變而不連續。 Mu等［75］將領-從結構和基于行為的編隊控制策略結合，形成一種新的編隊控制方法，如圖10所示。其中，領隊的軌跡設計方法采用基于樹拓撲數據和動態規劃理論的最優路徑規劃算法，性能指標為導彈和參考軌跡的縱向位移和橫向位移誤差。跟隨導彈設置了包括飛向目標、編隊保持、避碰/避障等行為來完成跟蹤領隊參考狀態的目的。另外，編隊組的決策基于外部環境和內部的傳遞共享，提高了系統容錯率。雖然算法簡單，但是很好地保證了控制精度。Zeng等［76］針對中段和末制導段設計了導彈制導律，在領-從結構框架上提出可協調的Dubins路徑規劃方法來同步中段飛行時間，過渡到末段后各自采用比例導引律攻擊目標，沒有考慮導彈之間的通信網絡，但該策略使得導彈編隊更具備靈活性。Zhao等［77］也基于領-從結構構建了主從式編隊控制框架，并附加考慮了視線角飽和約束條件。

在導彈編隊控制中，一致性理論除了用于控制算法設計外，還可以通過構建干擾觀測器對系統中存在的不確定性因素進行抑制和估計，從而減小和修正系統誤差。Wang等［78］基于領-從編隊模式，考慮參數不確定性、系統非線性及外部擾動等問題，在有限時間控制器中加入擾動觀測器進行抑制。仿真中加入正弦擾動對算法進行驗證，雖然結果能夠很好收斂，但是收斂速度仍需進一步改善，導彈加速度需給定邊界范圍。Yu等［79］采用一致性理論設計分布式擴展狀態觀測器對非匹配擾動和不確定項進行估計和補償。由于導彈編隊結構中具有多個領隊，建立了多導彈非線性跟蹤模型來代替線性模型，獲得了對擾動和不確定項一致的估計，克服了其對系統的影響。Liu等［80］在導彈動力學模型中考慮不確定性因素，進一步發展了一種全局分布式自適應時變編隊控制方法。該方法將控制律分為兩部分，一部分是通過一致性算法得到的主要控制項；另一部分是補償項，補償修正模型中的不確定因素。由此可看出，基于一致性理論的分布式協同控制方法在導彈編隊控制中同樣占據主流地位［81-82］。

可見，導彈編隊控制方法的研究思路與無人機是類似的，一致性理論框架結合其他編隊控制策略的控制方法對導彈集群系統同樣適用。在給定編隊控制策略后，先設計領隊個體的軌跡，然后根據控制理論對每個跟隨體分別設計跟蹤控制器跟蹤參考狀態，并額外考慮避障、隊形保持、外部擾動、不確定性等問題。但是受限于距離因素，當前研究結論中所考慮到的通信網絡拓撲結構均是理想情況下的信息傳遞，帶擾動、延遲、間斷等惡劣條件下的拓撲穩定性還需進一步研究。

同樣，現代控制理論及優化算法與主流編隊控制方法的結合可以獲得更優的編隊隊形和飛行彈道。Cui等［83］在文獻［74］結論的基礎上，將控制輸入多項式化，應用量詞消去理論設計導彈編隊重構控制能量最優彈道，然后采用位置誤差PD控制器跟蹤最優軌跡，其中，約束量包括重構的時間以及導彈的加速度。文獻基于閉環穩定系統假設以及一階連續性假設對編隊控制器進行設計，并沒有考慮不確定性影響等因素，研究還有欠缺。Wei等［84］對比了小擾動線性化方法和變換控制變量法的優劣，選擇了精度高但表達式復雜的變換控制變量法對最優編隊控制器進行推導，并通過線性二次理論克服了控制器中慢變或不變的擾動。Wei等［85］基于線性二次最優方法和變換控制變量法等技術，進一步對導彈編隊重構過程中可能存在的碰撞問題進行了研究，設計積分反饋-前饋（IFF）最優控制器，提出一種四層球面域碰撞規避系統，如圖11所示。當導彈之間的距離處于藍色范圍，導彈就必須進行機動來避免碰撞重新回到安全區域。Wu等［86］以領-從控制結構為基礎，設計了導彈空間距離最優離散反饋控制算法。領隊在收集跟隨者位置矢量、速度矢量信息等多約束信息條件后，由領隊設計制導算法，然后反饋給跟隨者。文獻推導了時變編隊約束下的通用形式，并采用偽譜法、一致性理論、人工勢場法等對每一時間節點的最優離散化問題進行求解。算法優勢明顯，但巨大的計算量在實際中不可取。Wang等［87］基于高斯偽譜法優化得到導彈可以達到指定編隊形狀的最優彈道， 與文獻［83］給定初始和終端編隊形狀再優化重構

軌跡的思路一致，考慮了導彈編隊初始和末端的位置約束、避障約束以及控制輸入約束，設計了魯棒控制器來跟蹤最優彈道下的

編隊構型，一定程度上解決了信息測量誤差帶來的擾動問題。Zhao等［88］針對編隊攔截機動目標的場景，提出一種時變編隊跟蹤控制方法（TFPBC），該方法基于領-從結構和一致性理論進行設計和推導。不足在于，文中采用了很多假設條件（如無向圖），沒有考慮不確定性條件，僅在二維平面進行了推導，使得設計的控制方法只能在特定條件下發揮作用。Zhang等［89］研究了不可控導彈速度條件下的編隊控制問題，采用領-從編隊結構構建相對運動方程，應用滑模變結構控制理論設計擾動條件下的編隊跟蹤控制器。不足在于，沒有考慮通信間斷、時延等問題，算法復雜，收斂速度相比經典算法還有待提高。

通過分析可知，在低速飛行器的編隊控制中，領隊-跟隨控制策略及其改進方法、行為控制法和虛擬結構控制法是對編隊隊形的確定，通常與一致性理論或其他控制方法結合來設計編隊控制器。同樣，一致性理論也可以結合其他控制方法進行應用，雖然一致性理論只給出了通信拓撲結構下的編隊方式，沒有具體編隊形狀，但增強了編隊隊形策略的靈活性，仍具有實踐意義。此外，研究發現，行為控制法和虛擬結構控制法在飛行器編隊控制中應用較少，當前研究趨勢仍以領隊-跟隨控制法和一致性理論為主進行拓展和創新。

3 高速飛行器編隊控制方法研究進展

相比低速飛行器，高速飛行器具有特殊的飛行特性——模型非線性強、飛行環境嚴峻、跨越空域廣、約束條件嚴苛等。高超聲速導彈作為目前主要發展的一種高速飛行器，主要分為滑翔式彈頭和吸氣式巡航導彈。根據彈道特征和動力特性，兩類導彈需要采取不同的協同控制策略。滑翔式彈頭屬于無動力再入滑翔飛行，只能依靠氣動力進行機動，因此，其編隊控制的可行性不強，主要通過調整飛行時間范圍實現末端到達時間一致性，或是通過母彈飛行到達指定位置后進行散布式飽和打擊。而具有動力推進的吸氣式巡航導彈具有更強的靈活性，在巡航段可以進行編隊控制，因此，可以借鑒低速導彈系統的編隊控制方法，在保證互相具有安全距離的前提下，編隊飛行至交班區域執行任務。由于高速飛行器的研究是一個新興領域，正處于加速發展階段，目前還沒有學者對高速飛行器的編隊控制方法進行總結。

特殊的飛行特性使得高速飛行器編隊控制更復雜，也更難以實現。Chen等［90］基于領-從編隊結構結合PD控制器和L1增強控制器驅動位置誤差歸零方法，為高超聲速飛行器編隊飛行控制提供了一種方案。其中，領隊負責指揮控制隊形，跟隨體跟從命令保持隊形或重構隊形。Zhang等［91］基于一致性理論提出以3枚高超聲速導彈為通信拓撲結構的編隊控制框架，并詳細推導和證明了分布式編隊控制律，約束條件為水平面相對位置。水曉冰等［92］針對高超聲速滑翔導彈提出在飛行速度不可控條件下通過控制飛行速度方向一致來實現基本的編隊，但是忽略了過程約束。Jia等［93］將高超聲速滑翔飛行器的飛行階段劃分后，在編隊飛行控制階段，采用一致性理論設計了二階編隊控制算法來保持相對位置，與文獻［91］采用了相同的通信拓撲結構。文獻［94］以多高超聲速導彈協同打擊固定目標為任務背景，創新性地提出一種交會與編隊飛行模式，將飛行階段分為交會段和編隊飛行階段，通過控制縱向和側向平面運動來實現協同，策略圖如圖12所示。飛行器經過自由避障飛行后，到達交會飛行段進行調整，隨后形成固定編隊飛行至目標區域圓周半徑50 km處，最后進行末制導段的綜合打擊。在編隊飛行階段，設計一條參考飛行軌跡后，在已構建編隊隊形的基礎上，每個個體通過控制縱向和側向飛行，嚴格跟蹤參考軌跡，從而達到編隊控制飛行的目的。陸浩然等［95］提出了一種基于偽譜法和自適應策略的高速飛行器編隊隊形快速成形實現方法。

除了編隊進行攻擊外，防御攔截也是高速飛行器需要編隊控制的重要應用。任章等［96］提出在目標不機動時保持攻擊編隊隊形，機動情況下改變攻擊編隊隊形，并且要在短時間內快速完成，是一項非常關鍵的科學問題。

可見，編隊控制在高速飛行器上的探索較為豐富，領隊-跟隨控制法和一致性理論在高速飛行器的編隊控制方案中仍是主流方向，但對于不確定性因素以及復雜條件的處理仍基于大量假設性條件和理想化場景，未來還需進一步深入研究。主要問題有：（1）由于信息傳遞和數據計算的延遲性與飛行器高速性的沖突，導致系統響應速度慢，編隊定位精度不高；（2）不確定性因素更廣泛，任何微小的誤差均會被系統響應放大，進而可能造成嚴重的影響，因此系統的容錯要求更高；（3）戰術戰略背景與編隊形式的高度統一，高速飛行器的編隊控制形式需要與作戰任務背景嚴格匹配。一方面是因為高速飛行器相比無人機和低速導彈造價昂貴，生產周期長，屬于高價值個體；另一方面，高速飛行器編隊控制需要與低速飛行器聯合進行綜合控制使得任務效率最大化，因此，需要更高的技術成熟度為未來的工程化研究奠定基礎。

對于高超聲速導彈來說，除編隊控制外，其他協同策略下的協同控制方法研究也比較豐富，包括基于攻擊時間控制制導（Impact Time Control Guidance，ITCG）方法的高超聲速導彈時間協同控制［97-99］、基于再入制導技術的高超聲速導彈時間協同控制［100-103］以及基于軌跡優化算法的高超聲速導彈時間協同控制［104-108］等。這些方法均通過協調飛行器飛行時間來實現協同，并不對編隊形式作限制，因此，相比于編隊飛行更容易實現，應用任務場景也更全面，但這些方法偏離于本文主題，在此不做過多贅述。

4 總結與展望

多飛行器編隊控制作為飛行器協同控制領域一項非常重要的課題，受到了大量學者的關注和研究。本文主要針對編隊控制這一典型協同控制形式在低/高速飛行器系統中的應用問題進行分析總結，得到如下結論：

（1） 四種主流編隊控制方法中，領隊-跟隨控制方法和一致性理論是研究低/高速飛行器編隊控制問題最廣泛的方法。這些編隊控制方法用于隊形控制（包括隊形形成、隊形保持和隊形變換），一般與其他控制理論或優化算法結合，才能形成一個完整的閉環系統。

（2） 不確定性因素（環境擾動、輸入偏差、測量誤差）、物理障礙等會對飛行器編隊控制產生較大影響，尤其在實際飛行當中，所面臨的環境條件更加復雜。目前低速和高速飛行器大部分研究都是基于理想條件取得的，未來需要重點考慮容錯控制問題以及擾動控制問題。

（3） 一致性理論作為研究編隊控制問題的熱點方法，涉及到的通信拓撲網絡的有效性和信息處理與傳遞的快速性，是影響控制算法可行性和穩定性的關鍵問題。目的就是要降低通信延遲，提高硬件計算速度，從而提高編隊控制的實時性。這在導彈編隊控制中尤其重要。

（4） 優化技術與編隊系統的深度結合，使得系統狀態的最優性成為新的發展需求。在實際控制環境需求下，協調各參數滿足飛行器穩定控制、獲得最小能量軌跡、系統狀態誤差最小等指標，可以最小化資源消耗，最大化任務效益。

基于上述結論，編隊控制需要解決的核心問題包括飛行器編隊控制的容錯性、實時性和最優性。主要關鍵技術包括：動態環境下集群容錯編隊控制、數據快速計算與處理、通信鏈路網絡化構建與維穩、不確定性估計與補償、基于分布式優化方法的編隊控制、異構飛行器編隊控制。

（1） 復雜環境下，數據快速計算與處理、通信鏈路網絡化構建與維穩以及不確定性估計與補償三個方面是首先要解決的問題。機載數據的快速處理直接體現在飛行器控制精度上，網絡化通信拓撲構建是實現大規模集群的關鍵一步，而不確定性問題則是在每一個環節都不可避免和忽視的問題，也直接決定控制的精準度。實際中飛行環境變化劇烈，構建穩定性和快速性的網絡鏈路才能保證飛行器之間的信息互通。其中，復雜動態通信網絡拓撲結構建模與優化是重要發展方向，要求信息傳遞速度快，環境抗干擾能力強，能適應異類飛行器之間的通信模式等； 同時，需要提高機載計算機的計算能力，以縮短系統傳遞和處理信息的時間。

（2） 容錯編隊控制研究的是在動態環境下，當編隊系統發生故障時系統該如何響應的問題。在飛行器編隊系統中，執行機構故障、系統參數失穩等是最常見的情況，可能造成整個編隊系統失去穩定控制的能力，因此，需要編隊系統具備自主故障監測和容錯控制能力。這種能力包括對可能出現故障問題的機構或參數給予較大的調整閾值，增大系統容忍度， 故障出現時改變控制器結構或控制方法，使之快速恢復正常狀態以及應用預測控制技術，使系統能夠自主對可能存在的故障或錯誤提前進行預測和警示。

（3） 一致性理論與優化方法的結合可以發展基于分布式優化方法的編隊控制。包括對資源調度和任務分配的協調分布式優化、分布式參數自適應機制、分布式協同目標跟蹤與控制等，這些過程都可以轉化成優化設計問題，以獲取滿足性能指標的結果。通過在子過程中嵌套優化過程，進而在整個編隊控制系統中融合發展成為更大的優化框架，使得每個環節都能達到最優性結果，這將極大支撐起未來大規模集群系統的協同控制。

（4） 低速飛行器和高速飛行器各自具有不同的飛行特性，其編隊控制問題也具有相當大的差異。發展低速與高速飛行器組成的異構飛行器編隊系統控制問題，將極大提高未來編隊系統綜合作戰能力，實現戰場效益最大化。低速與高速飛行器的編隊思路不能按常規的軌跡跟蹤方法來設計，必然是跨空域、跨地域等多場域結合的結果，發揮高速飛行器的隱蔽性和快速偵察能力，指揮低速飛行器集群飽和式打擊目標；或是低速飛行器偵察，指揮高速飛行器快速精確打擊目標等，都是未來的研究思路。此外，空地協同異構編隊也是未來發展的方向［109］。

（5） 打破編隊控制固定模式，發展基于深度學習和神經網絡的智能編隊控制方法是可行途徑，如無人機遇到障礙后自行變換隊形，導彈系統根據戰場態勢實時分配打擊目標，高速飛行器根據任務進行集體性行為決策等。通過整合每個飛行器的傳感信息和飛行器狀態，進行大量的行為判斷、行為決策等訓練學習，最終發展出一體化、智能化編隊控制框架，實現復雜的群體行為。

參考文獻：

［1］ Murphey R， Pardalos P M. Cooperative Control and Optimization［M］. Boston， MA： Springer， 2002.

［2］ 王佳楠， 王春彥， 王丹丹. 多飛行器協同控制理論及應用［M］. 北京： 科學出版社， 2020.

Wang Jianan， Wang Chunyan， Wang Dandan. Cooperative Control Theory and Application of Multiple Flight Vehicles［M］. Beijing： Science Press， 2020.（in Chinese）

［3］ 梁雯潔， 賈曉洪. 多飛行器自適應編隊制導控制技術［J］. 航空兵器， 2015（3）： 8-12.

Liang Wenjie， Jia Xiaohong. Adaptive Formation Guidance and Control Technology for Multi-Aircraft［J］. Aero Weaponry， 2015（3）： 8-12.（in Chinese）

［4］ 李鵬舉， 毛鵬軍， 耿乾， 等. 無人機集群技術研究現狀與趨勢［J］. 航空兵器， 2020， 27（4）： 25-32.

Li Pengju， Mao Pengjun， Geng Qian， et al. Research Status and Trend of UAV Swarm Technology［J］. Aero Weaponry， 2020， 27（4）： 25-32.（in Chinese）

［5］ 姚博譽， 路平， 楊森， 等. 四旋翼飛行器飛行控制技術綜述［J］. 航空兵器， 2020， 27（1）： 9-16.

Yao Boyu， Lu Ping， Yang Sen， et al. An Overview of Flight Control Technology for Quadrotor Aircrafts［J］. Aero Weaponry， 2020， 27（1）： 9-16.（in Chinese）

［6］ Wang P K C. Navigation Strategies for Multiple Autonomous Mobile Robots Moving in Formation［J］. Journal of Robotic Systems， 1991， 8（2）： 177-195.

［7］ Desai J P， Ostrowski J， Kumar V. Controlling Formations of Multiple Mobile Robots［C］∥IEEE International Conference on Robotics and Automation， 1998： 2864-2869.

［8］ Desai J P， Ostrowski J P， Kumar V. Modeling and Control of Formations of Nonholonomic Mobile Robots［J］. IEEE Transactions on Robotics and Automation， 2001， 17（6）： 905-908.

［9］ Fredslund J， Mataric M J. A General Algorithm for Robot Formations Using Local Sensing and Minimal Communication［J］. IEEE Transactions on Robotics and Automation， 2002， 18（5）： 837-846.

［10］ Beard R W， Lawton J， Hadaegh F Y. A Coordination Architecture for Spacecraft Formation Control［J］. IEEE Transactions on Control Systems Technology， 2001， 9（6）： 777-790.

［11］ Edwards D B， Bean T A， Odell D L， et al. A Leader-Follower Algorithm for Multiple AUV Formations［C］∥IEEE/OES Autonomous Underwater Vehicles， 2004： 40-46.

［12］ Shao J Y， Xie G M， Yu J Z， et al. Leader-Following Formation Control of Multiple Mobile Robots［C］∥IEEE International Symposium on Intelligent Control， Mediterrean Conference on Control and Automation， 2005： 808-813.

［13］ McDowell P， Chen J， Bourgeois B. UUV Teams， Control from a Biological Perspective［C］∥Oceans02 MTS/IEEE， 2002： 331-337.

［14］ Lee K H. An Optimal Control for Multiple Unmanned Underwater Crawling Vehicles［C］∥Oceans 2003. Celebrating the Past. Teaming Toward the Future，2003： 2649.

［15］ Campbell S， Naeem W， Irwin G W. A Review on Improving the Autonomy of Unmanned Surface Vehicles through Intelligent Collision Avoidance Manoeuvres［J］. Annual Reviews in Control， 2012， 36（2）： 267-283.

［16］ Tan K H， Lewis M A. Virtual Structures for High-Precision Coope-rative Mobile Robotic Control［C］∥IEEE/RSJ International Conference on Intelligent Robots and Systems， 1996： 132-139.

［17］ Lewis M A， Tan K H. High Precision Formation Control of Mobile Robots Using Virtual Structures［J］. Autonomous Robots， 1997， 4 （4）： 387-403.

［18］ Leonard N E， Fiorelli E. Virtual Leaders， Artificial Potentials and Coordinated Control of Groups［C］∥40th IEEE Conference on Decision and Control， 2001： 2968-2973.

［19］ Liu Y C， Bucknall R. A Survey of Formation Control and Motion Planning of Multiple Unmanned Vehicles［J］. Robotica， 2018， 36（7）： 1019-1047.

［20］ Askari A， Mortazavi M， Talebi H A. UAV Formation Control via the Virtual Structure Approach［J］. Journal of Aerospace Engineering， 2015， 28（1）： 04014047.

［21］ Kanjanawanishkul K. Coordinated Path Following for Mobile Robots Using a Virtual Structure Strategy with Model Predictive Control［J］. Automatika， 2014， 55（3）： 287-298.

［22］ Abbasi Y， Moosavian S A A， Novinzadeh A B. Formation Control of Aerial Robots Using Virtual Structure and New Fuzzy-Based Self-Tuning Synchronization［J］. Transactions of the Institute of Measurement and Control， 2017， 39（12）： 1906-1919.

［23］ Balch T， Arkin R C. Behavior-Based Formation Control for Multirobot Teams［J］. IEEE Transactions on Robotics and Automation， 1998， 14（6）： 926-939.

［24］ Song P， Han X B， Li K J， et al. Behavior-Based Formation Control of Nodes of Mobile Sensor Network［J］. Information-An International Interdisciplinary Journal， 2011， 14 （3）： 917-923.

［25］ Xu D D， Zhang X N， Zhu Z Q， et al. Behavior-Based Formation Control of Swarm Robots［J］. Mathematical Problems in Engineering， 2014， 2014： 205759.

［26］ Proetzsch M， Luksch T， Berns K. Development of Complex Robotic Systems Using the Behavior-Based Control Architecture iB2C［J］. Robotics and Autonomous Systems， 2010， 58（1）： 46-67.

［27］ Ropertz T， Berns K， Li X， et al. Verification of Behavior-Based Control Systems in Their Physical Environment［J］. MBMV， 2016： 128-137.

［28］ Lee G， Chwa D. Decentralized Behavior-Based Formation Control of Multiple Robots Considering Obstacle Avoidance［J］. Intelligent Service Robotics， 2018， 11（1）： 127-138.

［29］ Tsitsiklis J， Athans M. Convergence and Asymptotic Agreement in Distributed Decision Problems［J］. IEEE Transactions on Automatic Control， 1984， 29（1）： 42-50.

［30］ Lin Z Y， Broucke M， Francis B. Local Control Strategies for Groups of Mobile Autonomous Agents［C］∥42nd IEEE International Conference on Decision and Control， 2003： 1006-1011.

［31］ Olfati-Saber R， Murray R M. Consensus Problems in Networks of Agents with Switching Topology and Time-Delays［J］. IEEE Transactions on Automatic Control， 2004， 49（9）： 1520-1533.

［32］ Jadbabaie A， Lin J， Morse A S. Coordination of Groups of Mobile Autonomous Agents Using Nearest Neighbor Rules［J］. IEEE Transactions on Automatic Control， 2003， 48（6）： 988-1001.

［33］ Moreau L. Stability of Continuous-Time Distributed Consensus Algorithms［C］∥ 43rd IEEE Conference on Decision and Control （CDC）， 2004： 3998-4003.

［34］ Ren W， Beard R W. Consensus Seeking in Multiagent Systems under Dynamically Changing Interaction Topologies［J］. IEEE Transactions on Automatic Control， 2005， 50（5）： 655-661.

［35］ Tanner H G， Jadbabaie A， Pappas G J. Stable Flocking of Mobile Agents， Part Ⅰ： Fixed Topology［C］∥42nd IEEE International Conference on Decision and Control， 2003： 2010-2015.

［36］ Tanner H G， Jadbabaie A， Pappas G J. Stable Flocking of Mobile Agents， PartⅡ： Dynamic Topology［C］∥42nd IEEE International Conference on Decision and Control， 2003： 2016-2021.

［37］ Saber R O， Murray R M. Flocking with Obstacle Avoidance： Cooperation with Limited Communication in Mobile Networks［C］∥42nd IEEE International Conference on Decision and Control， 2003： 2022-2028.

［38］ Ren W. Consensus Strategies for Cooperative Control of Vehicle Formations［J］. IET Control Theory & Applications， 2007， 1（2）： 505-512.

［39］ Anderson B D O， Yu C B， Fidan B， et al. Rigid Graph Control Architectures for Autonomous Formations［J］. IEEE Control Systems Magazine， 2008， 28（6）： 48-63.

［40］ Luo X Y， Han N N， Guan X P. Leader-Following Consensus Protocols for Formation Control of Multi-Agent Network［J］. Journal of Systems Engineering and Electronics， 2011， 22（6）： 991-997.

［41］ Li W X， Chen Z Q， Liu Z X. Leader-Following Formation Control for Second-Order Multiagent Systems with Time-Varying Delay and Nonlinear Dynamics［J］. Nonlinear Dynamics， 2013， 72（4）： 803-812.

［42］ Wang J H， Han L， Li X D， et al. Time-Varying Formation of Se-cond-Order Discrete-Time Multi-Agent Systems under Non-Uniform Communication Delays and Switching Topology with Application to UAV Formation Flying［J］. IET Control Theory & Applications， 2020， 14（14）： 1947-1956.

［43］ Fax J A， Murray R M. Information Flow and Cooperative Control of Vehicle Formations［J］. IEEE Transactions on Automatic Control， 2004， 49 （9）： 1465-1476.

［44］ Jiang F C， Wang L. Finite-Time Information Consensus for Multi-Agent Systems with Fixed and Switching Topologies［J］. Physica D： Nonlinear Phenomena， 2009， 238（16）： 1550-1560.

［45］ Zhang H， Feng G， Yan H C， et al. Observer-Based Output Feedback Event-Triggered Control for Consensus of Multi-Agent Systems［J］. IEEE Transactions on Industrial Electronics， 2014， 61（9）： 4885-4894.

［46］ Ding D R， Wang Z D， Ho D W C， et al. Observer-Based Event-Triggering Consensus Control for Multiagent Systems with Lossy Sensors and Cyber-Attacks［J］. IEEE Transactions on Cyberne-tics， 2017， 47（8）： 1936-1947.

［47］ Lawton J R， Beard R W. Synchronized Multiple Spacecraft Rotations［J］. Automatica， 2002， 38（8）： 1359-1364.

［48］ Jose R， Dario F， Carlos N， et al. Leader-Following Graph-based Distributed Formation Control［J］.Robotica， 2008： 71-77.

［49］ Yoshioka C， Namerikawa T. Formation Control of Nonholonomic Multi-Vehicle Systems Based on Virtual Structure［J］. IFAC Proceedings Volumes， 2008， 41（2）： 5149-5154.

［50］ Ji Z J， Wang Z D， Lin H， et al. Interconnection Topologies for Multi-Agent Coordination under Leader-Follower Framework［J］. Automatica， 2009， 45（12）： 2857-2863.

［51］ Yu J L， Dong X W， Li Q D， et al. Time-Varying Formation Tracking for High-Order Multi-Agent Systems with Switching Topologies and a Leader of Bounded Unknown Input［J］. Journal of the Franklin Institute， 2018， 355（5）： 2808-2825.

［52］ Liu Z X， Yu X， Yuan C， et al. Leader-Follower Formation Control of Unmanned Aerial Vehicles with Fault Tolerant and Collision Avoidance Capabilities［C］∥International Conference on Unmanned Aircraft Systems （ICUAS）， IEEE， 2015： 1025-1030.

［53］ Yu Z Q， Zhang Y M， Jiang B， et al. Distributed Adaptive Fault-Tolerant Close Formation Flight Control of Multiple Trailing Fixed-Wing UAVs［J］. ISA Transactions， 2020， 106： 181-199.

［54］ Chen H， Wang X K， Shen L C， et al. Formation Flight of Fixed-Wing UAV Swarms： A Group-Based Hierarchical Approach［J］. Chinese Journal of Aeronautics， 2021， 34（2）： 504-515.

［55］ 朱旭， 張遜遜， 尤謹語， 等. 基于信息一致性的無人機緊密編隊集結控制［J］. 航空學報， 2015， 36（12）： 3919-3929.

Zhu Xu， Zhang Xunxun， You Jinyu， et al. Swarm Control of UAV Close Formation Based on Information Consensus［J］. Acta Aeronautica et Astronautica Sinica， 2015， 36（12）： 3919-3929.（in Chinese）

［56］ Dong X W， Yu B C， Shi Z Y， et al. Time-Varying Formation Control for Unmanned Aerial Vehicles： Theories and Applications［J］. IEEE Transactions on Control Systems Technology， 2015， 23（1）： 340-348.

［57］ Dong X W， Zhou Y， Ren Z， et al. Time-Varying Formation Control for Unmanned Aerial Vehicles with Switching Interaction Topologies［J］. Control Engineering Practice， 2016， 46： 26-36.

［58］ Dong X W， Li Y F， Lu C， et al. Time-Varying Formation Tracking for UAV Swarm Systems with Switching Directed Topologies［J］. IEEE Transactions on Neural Networks and Learning Systems， 2019， 30（12）： 3674-3685.

［59］ Xue Y H， Luo Y J， Zhu M. UAV Formation Control Method Based on Consistency Strategy［C］∥IOP Conference Series： Earth and Environmental Science， 2020， 440（5）： 052084.

［60］ He L， Sun X X， Lin Y. Distributed Output-Feedback Formation Tracking Control for Unmanned Aerial Vehicles［J］. International Journal of Systems Science， 2016， 47（16）： 3919-3928.

［61］ Zhang J L， Yan J G， Zhang P. Fixed-Wing UAV Formation Control Design with Collision Avoidance Based on an Improved Artificial Potential Field［J］. IEEE Access， 2018， 6： 78342-78351.

［62］ Kim S， Kim Y. Three Dimensional Optimum Controller for Multiple UAV Formation Flight Using Behavior-Based Decentralized Approach［C］∥ International Conference on Control， Automation and Systems，? 2007： 1387-1392.

［63］ Wang X H， Yadav V， Balakrishnan S N. Cooperative UAV Formation Flying with Obstacle/Collision Avoidance［J］. IEEE Transactions on Control Systems Technology， 2007， 15（4）： 672-679.

［64］ Zhao W H， Go T. 3-D Formulation of Formation Flight Based on Model Predictive Control with Collision Avoidance Scheme［C］∥48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition， 2010.

［65］ Ille M， Namerikawa T. Collision Avoidance between Multi-UAV-Systems Considering Formation Control Using MPC［C］∥IEEE International Conference on Advanced Intelligent Mechatronics， 2017： 651-656.

［66］ Cai Z H， Wang L H， Zhao J， et al. Virtual Target Guidance-Based Distributed Model Predictive Control for Formation Control of Multiple UAVs［J］. Chinese Journal of Aeronautics， 2020， 33（3）： 1037-1056.

［67］ Galzi D， Shtessel Y. UAV Formations Control Using High Order Sliding Modes［C］∥ American Control Conference， 2006.

［68］ Ullah N， Mehmood Y， Aslam J， et al. UAVs-UGV Leader Follower Formation Using Adaptive Non-Singular Terminal Super Twisting Sliding Mode Control［J］. IEEE Access， 2021， 9： 74385-74405.

［69］ Han K， Lee J， Kim Y. Unmanned Aerial Vehicle Swarm Control Using Potential Functions and Sliding Mode Control［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2008， 222（6）： 721-730.

［70］ Wang J N， Xin M. Integrated Optimal Formation Control of Multiple Unmanned Aerial Vehicles［J］. IEEE Transactions on Control Systems Technology， 2013， 21（5）： 1731-1744.

［71］ 周映江， 蔣國平， 周帆， 等. 基于滑模方法的分布式多無人機編隊控制［J］. 信息與控制， 2018， 47（3）： 306-313.

Zhou Yingjiang， Jiang Guoping， Zhou Fan， et al. Distributed Multi-UAV Formation Control Based on Sliding Mode Method［J］. Information and Control， 2018， 47（3）： 306-313.（in Chinese）

［72］ Kuo C W， Tsai C C， Lee C T. Intelligent Leader-Following Consensus Formation Control Using Recurrent Neural Networks for Small-Size Unmanned Helicopters［J］. IEEE Transactions on Systems， Man， and Cybernetics： Systems， 2021， 51（2）： 1288-1301.

［73］ Cui N G， Wei C Z， Guo J F， et al. Research on Missile Formation Control System［C］∥ International Conference on Mechatro-nics and Automation，? 2009： 4197-4202.

［74］ Wei C Z， Guo J F， Lu B G， et al. Adaptive Control for Missile Formation Keeping under Leader Information Unavailability［C］∥ 10th IEEE International Conference on Control and Automation， 2013： 902-907.

［75］ Mu X M， Du Y， Liu X， et al. Behavior-Based Formation Control of Multi-Missiles［C］∥ 21st Chinese Control and Decision Conference，? 2009： 5019-5023.

［76］ Zeng J， Dou L H， Xin B. A Joint Mid-Course and Terminal Course Cooperative Guidance Law for Multi-Missile Salvo Attack［J］. Chinese Journal of Aeronautics， 2018， 31（6）： 1311-1326.

［77］ Zhao J B， Yang S X. Integrated Cooperative Guidance Framework and Cooperative Guidance Law for Multi-Missile［J］. Chinese Journal of Aeronautics， 2018， 31（3）： 546-555.

［78］ Wang X F， Zheng Y Y， Lin H. Missile Formation Controller Design Based on Disturbance Observer and Finite-Time Control［J］. Journal of Beijing Institute of Technology， 2014， 23（4）： 427-434.

［79］ Yu J L， Dong X W， Li Q D， et al. Cooperative Integrated Practical Time-Varying Formation Tracking and Control for Multiple Missiles System［J］. Aerospace Science and Technology， 2019， 93： 105300.

［80］ Liu D Y， Liu H， Valavanis K P. Fully Distributed Time-Varying Formation Control for Multiple Uncertain Missiles［J］. IEEE Transactions on Aerospace and Electronic Systems， 2021， 57（3）： 1646-1656.

［81］ Zhu J W， Su D L， Sun H F， et al. Autonomous Cooperative Gui-dance Based on Distributed Consensus and Self-Management［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2021， 235（14）： 1968-1980.

［82］ Zhang S， Guo Y， Liu Z G， et al. Finite-Time Cooperative Gui-dance Strategy for Impact Angle and Time Control［J］. IEEE Transactions on Aerospace and Electronic Systems， 2021， 57（2）： 806-819.

［83］ Cui N G， Wei C Z， Guo J F， et al. Study on Missile Formation Reconfiguration Optimized Trajectory Generation and Control［J］. Journal of Applied Mechanics， 2010， 77（5）： 144-153.

［84］ Wei C Z， Shen Y， Ma X X， et al. Optimal Formation Keeping Control in Missile Cooperative Engagement［J］. Aircraft Engineering and Aerospace Technology， 2012， 84（6）： 376-389.

［85］ Wei C Z， Guo J F， Park S Y， et al. IFF Optimal Control for Missile Formation Reconfiguration in Cooperative Engagement［J］. Journal of Aerospace Engineering， 2015， 28（3）： 04014087.

［86］ Wu Y J， Zhu F T， Song C. Optimal Discretization of Feedback Control in Missile Formation［J］. Aerospace Science and Techno-logy， 2017， 67： 456-472.

［87］ Wang X F， Liu D Z， Tian Z. A Composite Formation Strategy for Multiple Missiles［C］∥ 3rd International Conference on Control， Automation and Robotics （ICCAR），? 2017： 684-691.

［88］ Zhao Q L， Dong X W， Song X， et al. Time-Varying Formation Pursuit Based Cooperative Guidance for Multiple Missiles to Intercept a Maneuvering Target［C］∥ 37th Chinese Control Conference （CCC）， 2018： 4779-4784.

［89］ Zhang Z L， Zhang K， Han Z G. A Novel Cooperative Control System of Multi-Missile Formation under Uncontrollable Speed［J］. IEEE Access， 2021， 9： 9753-9770.

［90］ Chen Q， Wan J， Ai J L. L1 Adaptive Controller Design for Hypersonic Formation Flight［J］. Science China： Technological Sciences， 2016， 59（10）： 1597-1608.

［91］ Zhang Y， Wang X， Tang S J. A Globally Fixed-Time Solution of Distributed Formation Control for Multiple Hypersonic Gliding Vehicles［J］. Aerospace Science and Technology， 2020， 98： 105643.

［92］ 水曉冰， 王曉芳， 林平， 等. 高超聲速飛行器編隊控制方法［J］. 戰術導彈技術， 2020（5）： 139-148.

Shui Xiaobing， Wang Xiaofang， Lin Ping， et al. A Formation Control Method of Multiple Hypersonic Missiles［J］. Tactical Missile Technology， 2020（5）： 139-148.（in Chinese）

［93］ Jia S W， Wang X， Li F G， et al. Distributed Analytical Formation Control and Cooperative Guidance for Gliding Vehicles［J］. International Journal of Aerospace Engineering， 2020： 8826968.

［94］ Yu W B， Yao Y Z， Chen W C. Analytical Cooperative Entry Guidance for Rendezvous and Formation Flight［J］. Acta Astronautica， 2020， 171： 118-138.

［95］ 陸浩然， 邱薇， 孫海亮， 等. 高速飛行器編隊隊形快速成形設計方法［J］. 航天控制， 2021， 39（2）： 33-38.

Lu Haoran， Qiu Wei， Sun Hailiang， et al. Design Method of Ra-pid Forming for High-Speed Aircraft Formation［J］. Aerospace Control， 2021， 39（2）： 33-38.（in Chinese）

［96］ 任章， 于江龍. 多臨近空間攔截器編隊攔截自主協同制導控制技術研究［J］. 導航定位與授時， 2018， 5（2）： 1-6.

Ren Zhang， Yu Jianglong. Research on the Autonomous Cooperative Guidance Control for the Formation Interception of Multiple Near Space Interceptors［J］. Navigation Positioning and Timing， 2018， 5（2）： 1-6.（in Chinese）

［97］ Jeon I S， Lee J I， Tahk M J. Impact-Time-Control Guidance Law for Anti-Ship Missiles［J］. IEEE Transactions on Control Systems Technology， 2006， 14（2）： 260-266.

［98］ Zhu C H， Xu G D， Wei C Z， et al. Impact-Time-Control Gui-dance Law for Hypersonic Missiles in Terminal Phase［J］. IEEE Access， 2020， 8： 44611-44621.

［99］ Wang J W， Zhang R. Terminal Guidance for a Hypersonic Vehicle with Impact Time Control［J］. Journal of Guidance， Control， and Dynamics， 2018， 41（8）： 1790-1798.

［100］ Liang Z X， Yu J L， Ren Z， et al. Trajectory Planning for Coopera-tive Flight of Two Hypersonic Entry Vehicles［C］∥21st AIAA International Space Planes and Hypersonics Technologies Conference， 2017.

［101］ Li Z H， He B， Wang M H， et al. Time-Coordination Entry Guidance for Multi-Hypersonic Vehicles［J］. Aerospace Science and Technology， 2019， 89： 123-135.

［102］ Yu J L， Dong X W， Li Q D， et al. Cooperative Guidance Strategy for Multiple Hypersonic Gliding Vehicles System［J］. Chinese Journal of Aeronautics， 2020， 33（3）： 990-1005.

［103］ Yu W B， Chen W C， Jiang Z G， et al. Analytical Entry Gui-dance for Coordinated Flight with Multiple No-Fly-Zone Constraints［J］. Aerospace Science and Technology， 2019， 84： 273-290.

［104］ Padhi R， Kothari M. Model Predictive Static Programming： A Computationally Efficient Technique for Suboptimal Control Design［J］. International Journal of Innovative Computing， Information and Control， 2009， 5 （2）： 399-411.

［105］ Chu H Y， Li J， Dong Y， et al. Improved MPSP Method-Based Cooperative Re-Entry Guidance for Hypersonic Gliding Vehicles［C］∥MATEC Web of Conferences， 2017， 114： 01002.

［106］ Wang Z B， Lu Y. Improved Sequential Convex Programming Algorithms for Entry Trajectory Optimization［J］. Journal of Spacecraft and Rockets， 2020， 57（6）： 1373-1386.

［107］ 劉哲， 陸浩然， 鄭偉， 等. 多滑翔飛行器時間協同軌跡快速規劃［J］. 航空學報， 2021， 42（11）： 524497.

Liu Zhe， Lu Haoran， Zheng Wei， et al. Rapid Time-Coordination Trajectory Planning Method for Multi-Glide Vehicles［J］. Acta Aeronautica et Astronautica Sinica， 2021， 42（11）： 524497.（in Chinese）

［108］ Zhou J， Lei H M. Coverage-Based Cooperative Target Acquisition for Hypersonic Interceptions［J］. Science China Technological Sciences， 2018， 61（10）： 1575-1587.

［109］ 周思全， 化永朝， 董希旺， 等. 面向空地協同作戰的無人機-無人車異構時變編隊跟蹤控制［J］. 航空兵器， 2019， 26（4）： 54-59.

Zhou Siquan， Hua Yongzhao， Dong Xiwang， et al. Air-Ground Time Varying Formation Tracking Control for Heterogeneous UAV-UGV Swarm System［J］. Aero Weaponry， 2019， 26（4）： 54-59.（in Chinese）

Research Progress of Formation-Cooperative Control Methods for

Low-Speed and High-Speed Vehicle Systems

An Kai1，Guo Zhenyun 1，Huang Wei1*，Xu Xiaoping2

（1. College of Aerospace Science and Engineering， National University of Defense Technology， Changsha 410073，China；

2. Beijing Interdisciplinary Center， National University of Defense Technology， Beijing 100101， China）

Abstract： As a typical cooperative control mode of multi-vehicle system， formation control can effectively solve the shortcomings of a single aircraft in information collecting， field detection， comprehensive attack and so on. This paper summarizes the research progress of formation control methods for low-speed and high-speed vehicle systems. Firstly， this paper introduces the basic concepts of four mainstream formation control strategies： leader-follower method， virtual structure method， behavior control method and consensus method， and analyzes their structural characteristics and strategic advantages. Then， based on these four methods， the control characteristics and performance differences of UAVs and low-speed missiles are summarized. The special flight characteristics make the formation control of high-speed vehicles have higher requirements for fault tolerance， rapidity and accuracy of system response， and then this paper mainly combs the theoretical practice and application exploration process of high-speed vehicles formation control， and puts forward the application problems that still need to be overcome. Finally， the development trend of vehicle formation control is prospected. The research can provide a reference for the future research on the theory and application of multi vehicle system formation control.

Key words： swarm intelligence；cooperative control； virtual? structure；behavior control；formation control；consensus control；vehicle

收稿日期：2022-04-08

基金項目：國家自然科學基金項目（11972368）；湖南省杰出青年自然科學基金項目（2021JJ10045）

作者簡介：安凱（1997-），男，甘肅臨澤人，博士研究生。

通信作者：黃偉（1982-），男，湖南長沙人，研究員。