優化估算題組教學的實踐研究

施小鋒

[摘 要]題組教學是根據學生的認知規律和思維能力，選用科學、合理、有效的一組具有漸進性的數學問題來組織課堂教學，實現有效教學的一種教學模式。基于SOLO分類理論，將學生數學學習的思維層次分為五個結構層次（水平）。在估算教學中通過借“題”夯“基”、順“勢”溫“度”、巧“變”顯“型”等教學策略，促進學生深度學習，提升學生的高階思維。

[關鍵詞]SOLO分類理論;估算;題組教學;高階思維

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2022）14-0015-03

高階思維是一種以高層次認知水平為主的綜合性能力，如批判性地評價信息的能力、解決問題的能力、創造性思維能力等。縱觀現行的估算教學，以下三“化”現象比較常見。

習題“零散化”：習題往往分散、孤立地出現，學生缺少綜合比較、系統思考的歷練。

功能“偏差化”： “怎么估”“看成多少”“結果是多少”等低效問答頻頻出現，雖然注重算法的習得，卻弱化了思維的發展。

思維“淺表化”：缺乏能激發學生高效、深度參與的活動和載體，學生只會覺得“要我估算我才估算”，思維淺化、窄化。

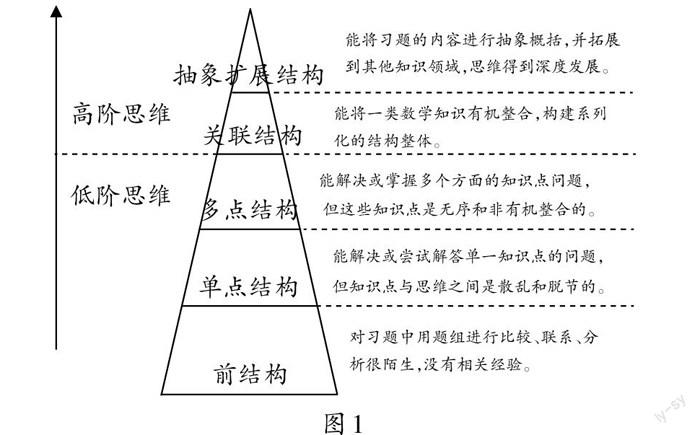
根據可視的學習結果，可以將學生數學學習的思維層次依據SOLO分類理論進行劃分（如圖1）。

估算對于提升學生的運算、推理、思維、表達等數學能力有著非常重要的意義。如何追本溯源，從源頭上消除三“化”現象，破解估算教學的難點？實踐表明，通過題組教學，能治標，更能治本。

本文以乘除法中的估算教學為例，借助題組教學，系統性地借“題”夯“基”、順“勢”溫“度”、巧“變”顯“型”，引導學生感知、理解與建構數學模型，促進高階思維的發生。

一、借“題”夯“基”，思維由“單點結構”走向“多點結構”

“單點結構”層次，是指能找到一個解決問題的方法或思路，然后憑這個方法或思路進行點對點的對接，以解決問題。“多點結構”是指能找到多種解決方法，但是這幾種方法之間是孤立的，而非整體和整合的。

根據題型的特點、題目的價值和功能構成的估算題組，可以讓學生感受到估算方法的多樣性，有效促進學生的思維從單點的一維走向多點的多維。

【例1】估算比大小：①252.4÷6.38和56×0.76;②4÷7和11÷23。

師：利用合適的估算方法比較每組中兩個算式的大小。說說是怎么估算的，為什么這么估算。

生1：題①252.4÷6.38可以估算成240÷6=40。估算56×0.76時，可以把56看成60，把0.76看成 0.8，得到48，比40大。故252.4÷6.38<56×0.76。

生2：把56和0.76都估大了，結果大太多了。可以把0.76看成[3/4]，56×0.76≈56×[3/4]=42，再與第一個算式比大小比較好。

師：很好！兩個數都估大，結果大太多了，這樣說服力不強。

生3：題②的4比7的一半大，而11不到23的一半，故4÷7>11÷23。

教師提煉多種算法。（1）就近取整估算。就近取整估算是教材中最“濃墨重彩”的，也是運用最廣泛、最有效的一種策略。整數是取整十、整百、整千數，小數是取整數或比原小數位數少一位或少幾位的近似小數。（2）分小數互化估算。在小數乘除法計算時，把小數轉化成接近的分數進行計算，會得到意想不到的簡便效果。（3）引入中間量估算。引入中間量往往用于結果的大小比較中。（4）簡潔性口訣估算。在乘法和除法中運用較為常見，就是在充分考慮數據特點情況下，直接利用乘法口訣估算結果。

教師將不同解法的習題“打包”整合成題組時，既要考慮到數據的一般性，也要考慮數據的特殊性，在數據的“取舍”與“進退”中培養學生思維的靈活性。

二、順“勢”溫“度”，思維由“多點結構”邁向“關聯結構”

“關聯結構”的形成，需要學生將同類型的數學知識有機整合，構建系列化、系統化的結構體。順著學生不同的思路，教師通過引導學生對解題方法的對比、聯系和優化，打破方法間的壁壘，讓學的思維從“多點結構”邁向“關聯結構”。

1.對比方法，挖掘算法拓寬度

在不同的習題中，即使是相同的數據也有不同的處理方式。利用題組可對比不同的處理方法，能增強學生思維的主動性和敏銳性，更好地拓寬學生的估算視野。

【例2】估算：（1）232÷5;（2）232÷8;（3）232÷7;（4）232÷11。

師：都是232除以一個自然數，怎么估算？

生1：232÷5≈250÷5;232÷8≈240÷8;232÷7≈210÷7;232÷11≈220÷11。

師：同樣是數據232，為什么估成的數卻不一樣？除數是多少時，才把232看成230？

生2：除數是23或者是10的時候。

估算應“先估后算”。估算的兩個重要因素是“方便計算”和“盡量接近”。通過題組對比，學生明白估算的方法是多元的、開放的，所要估的數不是一成不變的，需要根據參與運算的其他數的變化而變化。只有“高瞻遠矚”，深諳數據變化將引起估算方法改變之道理，增強方法間的融通與變化，才能拓展思維的寬度和廣度，“關聯”更多可能。

2.聯系方法，基于情境增厚度

相同的算式，在不同情境中的處理方法和結果會大相徑庭，而不同的情境又隱藏著相通的策略，此時可借助現實的數據情境進行教學。

【例3】（1）勝利小學有28個班，平均每班32人，共有980個座位的電影院能全部坐得下嗎？（2）加工車間要進貨28箱零件，每箱重32千克。一輛核定載重800千克的小車一次運完這些零件會超載嗎？

生1：題（1）用估大法。28×32≈30×32=960，比980小，因此坐得下。

生2：題（2）可以采用估小法。28×32≈28×30=840，比800大，所以超載了。

師：相同的算式28×32，處理方法為什么不一樣？如果都用估大或估小法可以嗎？

生3：如果被估部分估小了，結果還大，那就一定大;如果被估部分估大了，結果還小，那就一定小。

情境是數學知識和兒童思維之間的橋梁和紐帶。題組中的不同情境，可以讓抽象與具象呼應，不斷增強學生估算的變通性，增加學生思維的厚度，“關聯”則更持久。

3.優化方法，突現本質顯深度

解決一個問題，可以有多種策略，但一般都有一個相對簡潔、簡便的方法，在探尋與優化這個方法的過程中，需要學生具有批判性思維和創造性思維。

【例4】體育組要買一批跳繩，每根2.65元，五年級有172人，每人一根。（1）購物前思考“準備600元錢夠不夠”。（2）購物滿400元可送護腕，這次購物能否獲得贈送的護腕？（3）付款時思考“大約需要多少元錢”。（4）付款給收銀員時，一共需要付多少元錢？

師：這幾個小問題有什么區別和聯系？分別用什么方法解決？

生：前面三個問題不需要用精算，選用估算即可，分別選用“估大法”“估小法”“四舍五入法”取近似數。最后一個問題則必須用精算。

只有對解題策略和方法了然于胸，將精算與估算方法前后貫通，才能根據數據的特點并結合問題要求，適時選擇精算或估算，或合理、正確選擇估算的方法。在方法優與劣的對比中，在合適與不合適的甄別中，學生的思維向縱深處發展，“關聯”更自然、更堅固。

三、巧“變”顯“型”，思維由“關聯結構”躍至“抽象擴展結構”

“抽象擴展結構”是指學生能夠對問題進行抽象地概括，從理論的高度來分析問題，使問題本身的意義得到拓展和延伸。教師要在“關聯”的基礎上，引導學生繼續深入感受方法，并借助一定的符號，用簡單的方式進行表達，使學生在理解、運用和創造過程中更高效地理解估算的意義。

1.變封閉練習為開放建構

模型是一種高度抽象和概括的表達形式。開放題題組，可讓學生在對多個數據的假設和還原中感受方法的普適性和策略的統一性。

【例5】（1）2名教師帶著35名二年級學生去動物園參觀。成人票5.8元/張，兒童票2.8元/張，只帶120元錢夠不夠？

（2）將題（1）的數據進行調整：教師2名，票價5.□元，學生35名，票價2.□元，帶120元錢是否夠？

師：改編后，數據不確定，你還會做嗎？

生1：可以設一些數。先設幾個教師票的單價和學生票的單價，再估算，發現都比120元小。因此帶120元錢夠了。

生2：你這個方法比較麻煩！我是直接估算的，把教師票5.□看成6元，學生票2.□看成3元，總價不到120元。

師：這樣估算可以嗎？（有的學生認為可以;有的學生認為5.□可能更接近5元，學生票2.□可能更接近2元，因此不可以）

解決比較復雜的、條件不確定的估算問題時，可以引導學生通過“拎”（模型）、“定”（范圍）、“比”（大小）、“答”（問題）四步解答。

拎：5.□×2+2.□×35（ ? ?）120。

定： 5×2+2×35=80<5.□×2+2.□×35<6×2+3×35=117。

比：117<120。

答：117元是最多且不可能的情況，所以120元夠了。

因為改編后的習題數據不完整，使得精算“斷路”，所以在假設數據、分析數據的過程中，在提煉模型、深挖本質的過程中，學生的思維向高度抽象、深度建模發展。

2.變思維隱射為結果可視

從思維的角度，把抽象的表達轉向直觀的圖形，并借助直觀圖形來理解抽象的內容。在將思維“錨點”可視、外顯的過程中，學生能夠有抓手且直觀地學。

【例6】（改編例3）：勝利小學有28個班，平均每班32人，“恒達影城” 共有900個座位，能全部坐得下嗎？

生1：32×28≈32×30=960（估大法），比900大，坐不下。

生2：32×28≈30×28=840（估小法），比900小，坐得下。

生3：我是這樣想的，把32和28分別估成30，30×30=900。一個多估2，一個少估2，剛好抵消，能坐下。

生4：我喜歡生3的方法，但結果不應該剛好等于900。積的末位2乘8應該是6。

生5：我是實算（精算）的，32×28=896<900，坐得下。

師：生3說的一個多估2，一個少估2，剛好抵消，而生5精算出來是896，為什么不正好是900呢？

師（出示圖2）：相差的4在哪里？

先反思不同的解題思路得出的結果，再比較誤差。在“情理之中”卻又“意料之外”的辨析中，學生能夠借助直觀圖形進行解釋，思維逐漸深刻。

3.變順向思維為逆向思維

從模型出發，通過字母表達、文字說明、概括提煉等方法引領學生，能夠促進學生逆向思維能力的提升。

【例7】括號中可以填哪些自然數？（1）502×（ ?）≈3000;（2）6391÷（ ?）≈8。

生1：題（1）可把502看成500，利用等式性質求出結果是6。

生2：題（2）可把6391看成6400，商是8，不難推導出除數是800。

師：題（2）只能是800嗎？

生3：四舍五入后等于800的整數都可以，比如793、798、804等。

生4：題（2）可以轉化成“（ ?）×8≈6391”。把6391看成6400，看大了9，所以括號中最接近的整數是799。

生5：a×8≈6391，a就等于（6400-9）÷8=6400÷8-9÷8=800-1.125≈800。

要解答逆向思維的題組，就需要學生在運用模型解題的過程中對結果不斷進行調整和修正，思維的縝密性大大提高。

基于SOLO分類理論下的題組教學，是對估算教學中單一習題教學的超越，是對數學學科整體性、結構性和學生學習規律的順應。練習的負擔輕了、思維的含量多了——學生在題組計算中能夠聯系方法、比較異同、優化策略;機械化的操練減了、綜合化的運用增了——學生處理信息的能力更加“綜合”和“通盤”;碎片化的調取少了、模式化的通透多了——在解題組的過程中，在模式的提煉和運用過程中，學生的思維拾級而上。“題海”無涯苦作舟，題組則是茫茫“題海”中的思維之舟。

（責編 金 鈴）