在知識聯系中把握本質，在遷移運用中感悟通法

鄧昌濱

摘要：只注意按教材編排展開各種尺規作圖的新授教學是不夠的，會導致學生對尺規作圖內容的學習是碎片化的，而且可能無法深入。可以在學生學習了5個基本作圖后，安排一節跨教材章節的專題復習課，幫助學生建立基本作圖之間的聯系，認識作圖本質，并遷移解決更多作圖問題，學會自主探索作圖方法。

關鍵詞：尺規作圖;專題復習;知識體系;探索能力

尺規作圖（有限次地用無刻度直尺和圓規作圖），是一種限制工具的作圖，是初中數學的重要內容，其重要性在最近兩次義務教育數學課程標準修訂（2001年的實驗稿修訂為2011年版、2011年版修訂為2022年版）中都得到了加強。尺規作圖教學的基本要求和價值是，執果索因探索作圖方法，從而明確作圖原理，培養探索性思維和直觀想象、邏輯推理能力。

蘇科版初中數學教材中，尺規作圖內容跨躍三個年級，分散地和有關的知識點編排在一起，如下頁表1所示。因此，只注意按教材編排展開各種尺規作圖的新授教學是不夠的，會導致學生對尺規作圖內容的學習是碎片化的，而且可能無法深入——比如，學習“作一個角等于已知角”時，學生只能了解（記住）作圖方法，無法探索（發現）作圖方法，也無法證明（理解）作圖方法，因為還沒有學習三角形全等的知識。這樣的教學，往往不能很好地實現尺規作圖的教學價值：培養學生相應的思維能力，讓學生能夠遷移運用（尤其是針對現在流行的千變萬化的限制工具作圖問題）。

因此，可以在學生學習了5個“基本作圖”后，安排一節跨教材章節的專題復習課，幫助學生建立基本作圖之間的聯系，認識作圖本質，并遷移解決更多作圖問題，學會自主探索作圖方法。下面呈現具體的教學設計，并對教學立意做進一步的闡釋。值得一提的是，這節課曾在中國教育學會中學數學教學專業委員會組織的第十二屆初中青年數學教師優秀課展示活動中展示。

一、教學設計

（一）文化引入

師（出示圖1）在古代的女媧伏羲圖中，女媧手執規，伏羲手執矩（曲尺）。這代表規矩和制度的產生，告誡我們，萬物皆有定律，凡事都要遵守規范。歷史上，最先明確提出限制作圖工具的是古希臘的伊諾皮迪斯，之后，限用尺規工具作圖逐漸成為一種公約。多年來，很多數學家都曾致力于研究尺規作圖三大問題，即倍立方積、三等分任意角和化圓為方，但都以失敗而告終。直至1882年，才證實了這些都是尺規作圖不可能問題。近幾年，限定工具、限定次數的作圖問題成為中考數學的熱點問題。

課始，介紹尺規作圖的歷史，以及數學家致力于解決尺規作圖三大不可能問題的艱難歷程，讓學生感受到數學家追求真理的理性精神，激發學生的求知欲望和信心，發揮數學學科的育人價值，順勢引入課題。

（二）問題驅動，構建知識體系

教師拿出一根細繩，然后對折，引導學生從生活的視角尋找中點;接著，把細繩抽象成一條線段，引導學生從數學的視角尋求中點，從而引入用尺規作線段的垂直平分線的必要性，也體現了數學來源于生活的理念。

問題1怎樣用尺規作線段AB的垂直平分線？

追問1直尺與圓規在作圖中分別起什么作用？

追問2你是怎么想到這種作法的？

追問3如何證明所作直線是AB的垂直平分線？

追問4運用尺規，還有其他方法作線段AB的垂直平分線嗎？

問題1引導學生回顧教材中已知線段的垂直平分線的基本作法，從數學的角度解決之前提出的找線段中點的問題。

追問1引導學生思考尺規作圖的本質，認識直尺可以作出不確定（不過定點或過一個定點）或確定（過兩個定點）的直線、射線或線段，圓規可以作出不確定（圓心或半徑不確定）或確定（圓心和半徑確定）的圓或弧，進而可以通過交點（交軌法），確定更多的線段或弧，以及更多的交點……同時，幫助學生復習“作一條線段等于已知線段”這一尺規最簡單運用、交軌法最簡單體現（一條直線、一段弧相交）的基本作圖，認識到這是其他基本乃至非基本作圖的“最基礎”。

追問2引導學生回顧新授課中探索作圖方法的過程，感受執果索因（假設圖形已經作出），根據圖形和目標、條件聯想所學知識（幾何性質），尋找可以作出的圖形及其能夠滿足的性質的思想方法。如果新授課沒有做好這方面的教學，本節課需要特別加強，因為這樣的思想方法是解決作圖問題的通法（基本思路）。

追問3引導學生在探索作圖方法的基礎上明晰作圖原理，具體來說，即弄清作線段垂直平分線的依據是線段垂直平分線定理的逆定理。

追問4鼓勵學生從不同的視角尋求不同的作法，避免思維固化，進一步感受通法以及原理的豐富內涵和引領作用，培養發散思維。具體來說，可以引導學生改變長度（半徑）或位置（在線段的同側或異側），得到另一個交點（如圖2、圖3所示）。

問題2O是直線l外一點，怎樣用尺規作過點O的直線l的垂線？

追問將點O移至直線l上，又如何作？

問題2及追問引導學生回顧教材中過一點的已知直線的垂線的基本作法（如圖4、圖5所示）。在作圖過程中，學生能感受到，第一步實際上是構造一條線段，第二步實際上是作出所構造線段的垂直平分線，只不過這時只需讓兩弧交于一點，因為有一個已知點了。由此，學生能認識到，從作法上看，過一點作已知直線的垂線可以看作作已知線段的垂直平分線的變式。

問題3若變為一般的角，仍這樣作圖，是否也能作出角的平分線？

問題3引導學生回顧教材中已知角的平分線的基本作法，如圖6。但這里改變了問法，直接提示了它的思路來源，即與前一種作圖的關系。由此，學生很容易發現，作已知角的平分線是過直線上一點作已知直線的垂線的一般情況（直線及其上一點可以看作一個平角）。

問題4上述基本作圖有何共同特征？

這是本節課的關鍵問題之一。通過前三個問題，學生已經初步感受到三種基本作圖之間的聯系。這里進一步引導學生挖掘它們的關系，提煉它們的共同特征。首先，要讓學生認識到作圖對象之間從特殊到一般的關系，即垂線是中垂線的一般化，角平分線是垂線的一般化（如圖7所示）;并感受到作圖方法之間逆向的從一般到特殊的轉化。其次，要讓學生認識到三種作圖的共同特征，即利用“邊邊邊”的基本事實構造有一組公共邊且關于這組公共邊軸對稱的兩個全等三角形（在圖7的各個圖形中即深淺不同的灰底標記的兩個三角形）。在此基礎上，還要引導學生思考為什么作法的內核（本質）都是這樣的，從而認識到：線段是比角更基本的圖形（度量），尺規的基本功能是作線段，從線段到角除了簡單的等腰三角形的性質之外，可運用的最基本的性質就是由“邊邊邊”確定的三角形全等，即三角形穩定性的具體表現（實際上“等邊對等角”也是通過由“邊邊邊”確定的三角形全等證明的）。

問題5現在你能探索并證明作一個角等于已知角的方法了嗎？

新授課中，學生因為沒有學習有關的知識，所以不能探索和證明作一個角等于已知角的方法。現在，學生不僅具備了有關的知識，而且在建立另外三種基本作圖聯系的過程中，認識到尺規作圖的本質，因而很容易得到：要作一個角等于已知角，可以通過三條邊對應相等，作一個三角形全等于已知三角形;教材中的基本作法正是這樣得到（基于這一原理）的，只不過它在已知角的基礎上構造了一個等腰三角形，再作其全等三角形，而我們也可以構造一個任意三角形。

至此，5種基本作圖及其相互關系、內在本質都已經得到了“再認識”。

（三）習題引領，提升探索能力

例1如圖8，已知△ABC，請用尺規作△ABD（點D不與點C重合），使得它與△ABC全等。

變式1如圖9（1），已知△ABD≌△ABC，僅用無刻度的直尺，過點C作AB的垂線。

變式2如圖9（2），已知△ABD≌△BAC，僅用無刻度的直尺，作AB的垂直平分線。

變式3如圖9（3），已知△ABD≌△BAC，僅用無刻度的直尺，找到AB的中點。

前面，學生已經認識到通過“邊邊邊”作三角形全等對于基本作圖的重要性。進一步的作圖探索，便從限制一條邊為公共邊作已知三角形的全等三角形開始。對此，學生很容易發現，關鍵是作出AD、BD，使得AD=AC、BD=BC或AD=BC、BD=AC，運用交軌法得到點D的位置。顯然，有三種可能的結果（如圖9所示，可以引導學生借助三角形紙片擺一擺，做到不重不漏），能培養學生思維的縝密性。當然，本題還具有一定的開放性，也可以設法作點C關于直線AB的對稱點、關于線段AB中垂線的對稱點或關于線段AB中點的對稱點，即為點D。由此，可以進一步培養學生思維的發散性。

三個變式在例1探究結果的基礎上，很自然地由尺規作圖過渡到更為一般的限制工具作圖（這里是只用無刻度的直尺作圖）。引導學生執果索因，聯想有關的知識，學生不難探索（證明）出作圖方法：對變式1，直接連接CD即可;對變式2，設AD與BC的交點為E，分別延長CA與DB，交于點F，然后連接EF即可;對變式3，直接連接CD，找到其與AB的交點即可。由此，學生能夠充分感悟到，限制工具作圖的關鍵是利用好圖形的幾何性質，充分的推理思考能夠代替（簡化）復雜的作圖步驟。

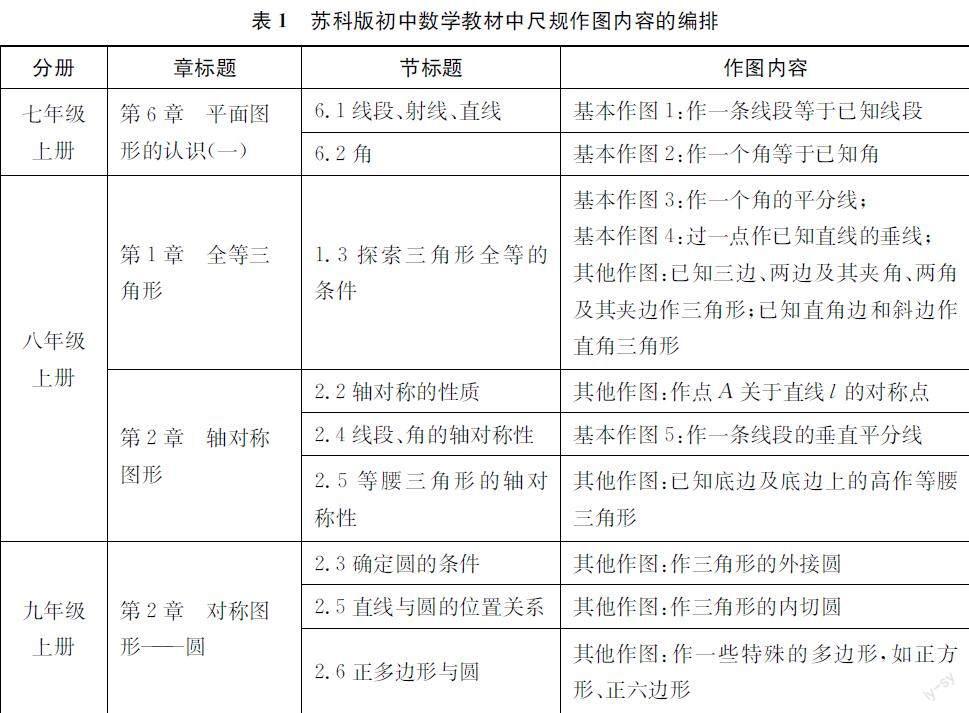
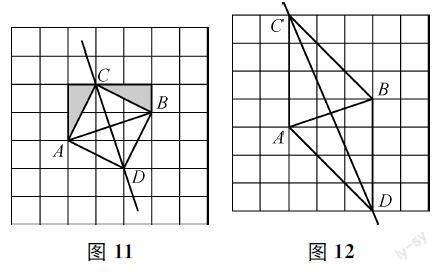
例2如圖10，在正方形網格中，A、B兩點均在格點上，你能僅用無刻度的直尺作AB的垂直平分線嗎？（保留作圖痕跡）

網格背景下的限制工具作圖是當下中考考查的熱點。網格實際上給出了平面相互垂直的兩個維度上的整數度量，本質是平面直角坐標系的離散化形式。其中，可以精確利用的只有格點，任意格點的連線總是某個直角三角形的直角邊或斜邊。因此，可以借助勾股定理或直角三角形全等，得到線段的度量或關系。這在一定程度上可以代替圓規的度量（本質是比較）作用。引導學生認識到網格背景的本質，學生便不難找到與點A、B距離相等的兩個格點（即下頁圖11中的點C、D），從而作出AB的垂直平分線。此外，教學中，還可以引導學生剖析如下頁圖12所示的典型錯例，認識到格點連線的度量或關系只能通過計算或推理得到，不能憑感覺，也不能通過測量（這不能保證精確）——這其實正是初中的論證幾何與小學的實驗幾何的主要區別。

例3在空白正方形中，用尺規設計一個圖案，使其具有對稱性或其他方面的美感（意味），并說明你希望表達的含義。

設計一個極具開放性的問題，引發學生的應用意識與創新思維，發展學生的審美感知與數學直覺，深化學生對尺規作圖本質與價值的認識。學生通過連線、作圓（弧）、找中點等基本作圖活動，能夠設計出如圖13所示的各種或簡單或復雜的具有對稱性的圖案。如果學生的聯想能力較強，還可能設計出七巧板圖案（如圖14所示）。

（四）課堂小結

最后，讓學生談談經過本節課的學習對尺規作圖有哪些新的認識，引導學生理清基本作圖之間的關系，把握作圖本質，體會基本作圖與非基本作圖、尺規作圖與限制工具作圖之間的聯系，感悟如何探索作圖方法、明確作圖原理。

二、教學立意的進一步闡釋

本節課是跨教材章節內容的專題復習課，主要體現了以下幾點立意：

第一，在知識聯系中把握本質。學生學過的尺規作圖，尤其是基本作圖知識，是零散的、碎片化的。本節課通過環環相扣的問題鏈，重構學習順序，引導學生一步步發現它們之間的聯系，在此基礎上認識它們的本質，包括尺規的連線、作圓（弧）、度量（比較）等基本功能以及作圖的交軌定點、以點定線（弧）、以線（長度）定角（角度）等基本思路，從而建立知識體系，實現深度理解。

第二，在遷移運用中感悟通法。尺規作圖知識更重要的教學價值在于讓學生學會執果索因（由“效果圖”找“施工圖”）探索解決幾何問題（在“知何由以知其所以然”的過程中自然地“知其所以然”“知其然”），感悟其中普適的、可遷移的思想方法（活動經驗），提升問題探究能力。本節課自然地從基本作圖問題過渡到非基本作圖問題，再過渡到更一般的限制工具作圖問題，最后過渡到自由創作的設計圖案問題（因為課堂時間限制，沒有安排更多類型或特點的作圖問題），引導學生在遷移運用中，深度分析作法來源及作圖原理，感悟解決作圖問題的通法及其廣泛的應用價值。

此外，本節課滲透的數學文化、提供的設計圖案任務，能很好地發揮數學的文化價值和審美價值，潤澤學生的數學學習情感;設計的錯例剖析活動，能強化數學的理性特質，涵養學生的理性精神。這些都豐盈了本節課的育人內涵。