以問題驅動探究 促學生自主建構

楊書剛

[摘 ?要] “問題”“自主”“高效”等詞語，是新課改實施后的流行詞，以問題驅動探究，促進學生自主建構的教學模式，是如今數學教學改革的主要取向. 文章以“導數在函數研究中的應用（單調性）”教學為例，具體從“情境創設，提出問題”“問題驅動，合作探究”“驗證猜想，建構新知”“拓展延伸，深化理解”“實際應用，鞏固提升”“及時反思，總結提煉”等方面，談談教學實施過程與思考.

[關鍵詞] 問題驅動;自主建構;課堂探究

數學教學的核心任務是引導學生在體驗中，感知知識的發生和發展過程，讓學生自主建構完整的認知體系，以促進各項數學能力的發展[1]. 實踐證明，“問題引領，自主建構”的教學模式，能有效驅動學生的探究意識，讓學生在深度思維中突破自主建構的瓶頸階段，成為數學信息的加工主體和知識的建構者.

然而調查發現，當前的教學實踐中，教師設計的問題有的過于簡單、膚淺，缺乏探究價值，課堂表面上欣欣向榮，而學生的思維卻得不到有效訓練;有的過于深奧，超越了大部分學生的認知水平，學生無從下手，只能以“注入”的方式實施知識教學，導致主動建構過程缺失. 這兩種情況都無法讓學生建構完整、穩固的認知體系.

究竟該如何設計具有實際教學意義的問題，引發學生的自主探究，實現知識的自主建構呢？本文以“導數在函數研究中的應用（單調性）”教學為例，談幾點思考.

[?]教學設計

1. 情境創設，提出問題

新課標高度重視教學中問題情境的創設，但教材中所呈現的情境常具有較大的跳躍性，對學生而言稍顯粗糙. 為了驅動學生對新知的探究興趣，教師應在教材編者的思路與知識邏輯的基礎上，結合學生的實際認知需求，進行問題情境的整理與重構，以激發學生的認知沖突，啟發思維，為探究奠定基礎.

問題1 某地區的氣溫變化數據顯示凌晨2時到5時的溫度f（x）和時間x接近函數f（x）=，請分析一下這段時間的氣溫f（x）隨著時間x的變化，出現了怎樣的趨勢.

生1：或許可以將該問題轉化為研究f（x）=（x∈[2，5]）單調性的問題？

師：大家還記得如何判斷一個函數的單調性嗎？

生2：可以用定義法或描點法來判斷.

師：這個問題是否能用這兩種方法解決呢？

生3：貌似不行，用描點法畫圖時，存在的誤差比較大，而用定義法運算，對f（x）-f（x）的符號又難以確定.

問題2 也就是說我們現在遇到了一個無法用單調性定義的“老方法”解決的新問題，此時該怎么辦呢？

生4：或許可以尋找一種新的突破方法.

設計意圖 與學生生活相關的問題情境，讓學生感知“數學源自生活，數學知識又為生活服務”的理念. 隨著問題的探索，學生發現用原有的認知無法解決新的問題. 隨著認知沖突的產生，順利地激發了學生深入探究的興趣.

2. 問題驅動，合作探究

知識意義的建構與問題的形成與探究是同步推進、相伴相隨的關系. 隨著核心問題的提出，接下來就是對問題的探究. 俗話說：“單絲不成線，孤木不成林.”一個人的智慧是有限的，而團體的智慧卻是無窮的. 因此，面對一個學生認知之外的問題，最好的方式就是合作探究，發揮團體的力量，展開對知識的探索.

問題3 接下來我們再次回到函數單調性的定義，以小組合作交流的方式，看看是否有新的收獲.

（小組合作交流）

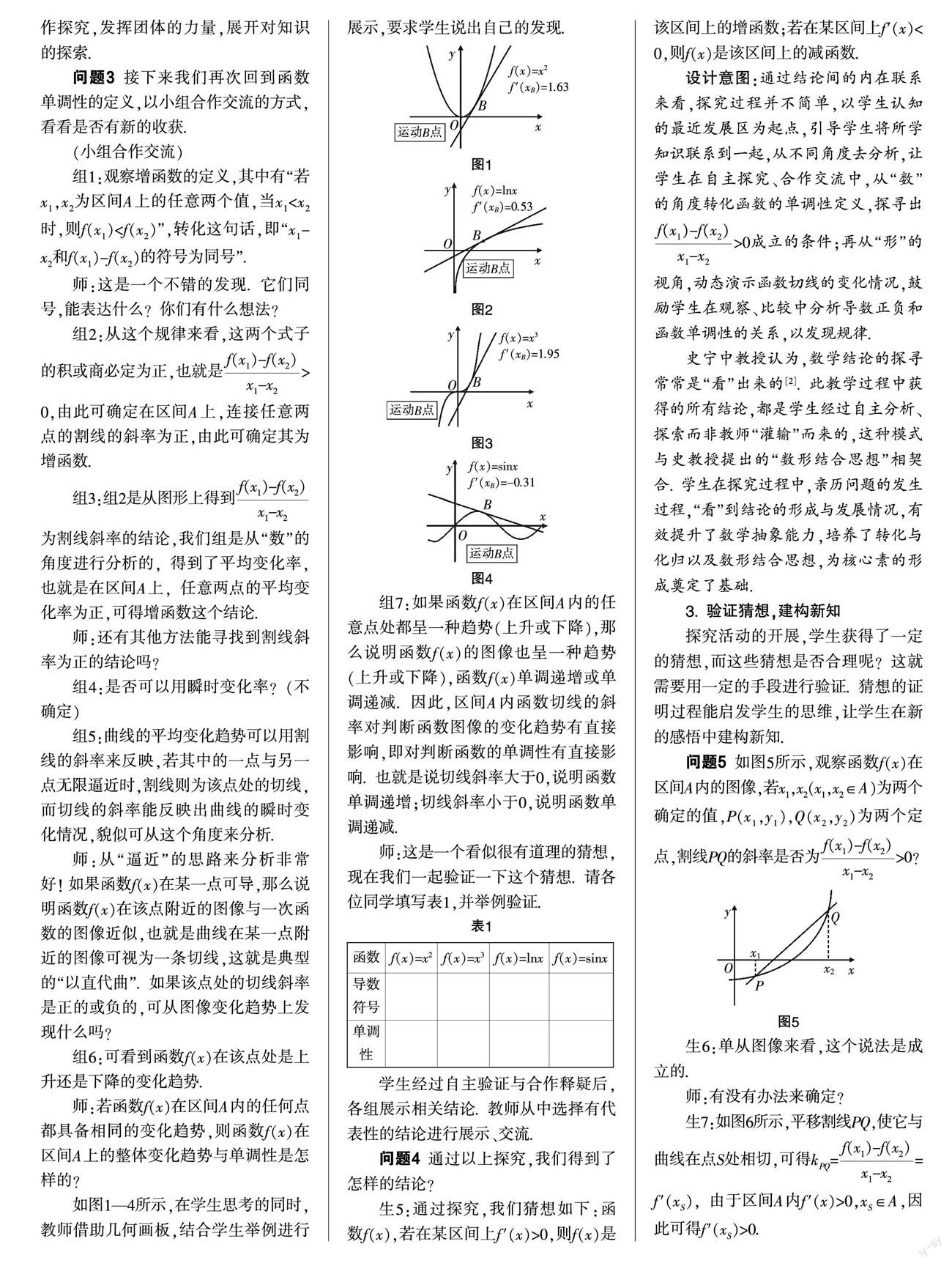
組1：觀察增函數的定義，其中有“若x，x為區間A上的任意兩個值，當x

師：這是一個不錯的發現. 它們同號，能表達什么？你們有什么想法？

組2：從這個規律來看，這兩個式子的積或商必定為正，也就是>0，由此可確定在區間A上，連接任意兩點的割線的斜率為正，由此可確定其為增函數.

組3：組2是從圖形上得到為割線斜率的結論，我們組是從“數”的角度進行分析的，得到了平均變化率，也就是在區間A上，任意兩點的平均變化率為正，可得增函數這個結論.

師：還有其他方法能尋找到割線斜率為正的結論嗎？

組4：是否可以用瞬時變化率？（不確定）

組5：曲線的平均變化趨勢可以用割線的斜率來反映，若其中的一點與另一點無限逼近時，割線則為該點處的切線，而切線的斜率能反映出曲線的瞬時變化情況，貌似可從這個角度來分析.

師：從“逼近”的思路來分析非常好！如果函數f（x）在某一點可導，那么說明函數f（x）在該點附近的圖像與一次函數的圖像近似，也就是曲線在某一點附近的圖像可視為一條切線，這就是典型的“以直代曲”. 如果該點處的切線斜率是正的或負的，可從圖像變化趨勢上發現什么嗎？

組6：可看到函數f（x）在該點處是上升還是下降的變化趨勢.

師：若函數f（x）在區間A內的任何點都具備相同的變化趨勢，則函數f（x）在區間A上的整體變化趨勢與單調性是怎樣的？

如圖1—4所示，在學生思考的同時，教師借助幾何畫板，結合學生舉例進行展示，要求學生說出自己的發現.

組7：如果函數f（x）在區間A內的任意點處都呈一種趨勢（上升或下降），那么說明函數f（x）的圖像也呈一種趨勢（上升或下降），函數f（x）單調遞增或單調遞減. 因此，區間A內函數切線的斜率對判斷函數圖像的變化趨勢有直接影響，即對判斷函數的單調性有直接影響. 也就是說切線斜率大于0，說明函數單調遞增;切線斜率小于0，說明函數單調遞減.

師：這是一個看似很有道理的猜想，現在我們一起驗證一下這個猜想. 請各位同學填寫表1，并舉例驗證.

學生經過自主驗證與合作釋疑后，各組展示相關結論. 教師從中選擇有代表性的結論進行展示、交流.

問題4 通過以上探究，我們得到了怎樣的結論？

生5：通過探究，我們猜想如下：函數f（x），若在某區間上f′（x）>0，則f（x）是該區間上的增函數;若在某區間上f′（x）<0，則f（x）是該區間上的減函數.

設計意圖：通過結論間的內在聯系來看，探究過程并不簡單，以學生認知的最近發展區為起點，引導學生將所學知識聯系到一起，從不同角度去分析，讓學生在自主探究、合作交流中，從“數”的角度轉化函數的單調性定義，探尋出>0成立的條件;再從“形”的視角，動態演示函數切線的變化情況，鼓勵學生在觀察、比較中分析導數正負和函數單調性的關系，以發現規律.

史寧中教授認為，數學結論的探尋常常是“看”出來的[2]. 此教學過程中獲得的所有結論，都是學生經過自主分析、探索而非教師“灌輸”而來的，這種模式與史教授提出的“數形結合思想”相契合. 學生在探究過程中，親歷問題的發生過程，“看”到結論的形成與發展情況，有效提升了數學抽象能力，培養了轉化與化歸以及數形結合思想，為核心素的形成奠定了基礎.

3. 驗證猜想，建構新知

探究活動的開展，學生獲得了一定的猜想，而這些猜想是否合理呢？這就需要用一定的手段進行驗證. 猜想的證明過程能啟發學生的思維，讓學生在新的感悟中建構新知.

問題5 如圖5所示，觀察函數f（x）在區間A內的圖像，若x，x（x，x∈A）為兩個確定的值，P（x，y），Q（x，y）為兩個定點，割線PQ的斜率是否為>0？

生6：單從圖像來看，這個說法是成立的.

師：有沒有辦法來確定？

生7：如圖6所示，平移割線PQ，使它與曲線在點S處相切，可得k==f′（x），由于區間A內f′（x）>0，x∈A，因此可得f′（x）>0.

問題6 若P，Q為區間A內曲線上的任意兩點，還能確保f′（x）>0成立嗎？

生8：若P，Q為區間A內曲線上的任意兩點，因為區間A內f′（x）>0，可確定f′（x）=>0恒成立. 雖然點S會隨著點P，Q的變化而改變，無法確定點S的具體位置，但它一直存在.

師：太精辟了！的確，雖然不知道點S的位置具體在哪里，但它確實存在. 現在請大家根據以上驗證情況，說說你們的結論.

生9：對于函數f（x），在某個區間上若f′（x）大于零，則f（x）是這個區間上的增函數;在某個區間上若f′（x）小于零，則f（x）是這個區間上的減函數;若f′（x）恰巧為零，則f（x）是這個區間上的常數函數.

設計意圖：證明猜想的結論有一定難度，有些教師怕麻煩，就讓學生直接記住結論，而后引導學生實際應用結論. 如此，或許課堂氛圍也和諧，學生的正確率也不錯，但學生對結論的理解會永遠停留在表淺階段，對導數正負和函數單調性的關系一知半解，這為后期解決綜合性問題埋下了隱患.

缺乏驗證的結論，用起來就像無源之水. 而循循善誘、由淺入深地引導學生驗證猜想，不僅能突破教學難點，也能啟發思維，挖掘出該結論真正意義上的教學價值，為后期微積分的學習夯實了基礎.

4. 拓展延伸，深化理解

問題7 同學們總結得很到位，那么該結論的逆命題是否成立呢？即若f（x）在某個區間上是增函數，則在此區間上f′（x）>0是否成立？

生10：不成立，借助幾何畫板能夠發現f（x）=x3在R內是增函數，但是f′（0）=0.

師：也就是說，若f（x）在某個區間上是增函數，則在此區間上f′（x）≥0. 反之，若在某個區間上，已知f′（x）≥0，則f（x）在該區間上是增函數. 這種說法合理嗎？

生11：這種說法不合理，f′（x）≥0存在f′（x）>0和f′（x）=0兩種情況，而f′（x）=0說明f（x）為常數函數，并不具備單調性特征.

問題8 我們應該怎么表述，才能讓命題成立？

生12：在某個區間上，如果f′（x）≥0，同時此區間的任何一個子區間上的f′（x）≠0，那么f（x）在這個區間上是增函數. 其中有一個特殊情況，即若干個不連續的點處的導數是可以為零的.

設計意圖：引領學生在親自觀察、交流與體驗中參與問題的設計，在對逆命題的研究中，促進學生逆向思維的發展，從而使其有效地深入理解問題的本質，提升思辨能力.

5. 實際應用，鞏固提升

練習1：函數f（x）=2x3-5x2+7位于哪些區間上是增函數？

練習2：怎么確定函數f（x）=sinx（x∈（0，3π））的單調遞減區間？

練習3：思考函數f（x）=（x∈[2，5]）具備怎樣的單調性.

設計意圖：課堂練習是深化學生對知識理解與應用的過程，讓學生在練習中通過模仿、辨識建構認知. 練習逐層深入，由淺入深，使學生深切體會在問題驅動下，探究的實際價值.

6. 及時反思，總結提煉

師：通過本節課的學習，大家有什么收獲？

生13：本節課中，我們應用了以直代曲、轉化與化歸以及數形結合等數學思想方法，這幾個數學思想方法能簡化問題，為后繼的解題服務.

[?]教學思考

1. 將教學目標作為問題的出發點

教學活動都是圍繞教學目標而開展的，教學目標是一節課的方向目標，它決定著本節課教師該教些什么，學生要學些什么，對知識的理解應達到怎樣的程度，獲得怎樣的能力，等等. 只有深刻理解教學目標，才能精準設計問題，讓學生明確探究方向.

本節課揭示的導數與函數單調性的概念比較抽象，而且是教學重點之一. 因此，教師首先引導學生回顧原有的知識，然后結合學生的實際情況，引導學生開展深入、有效的探究活動，為知識的建構奠定基礎.

2. 將最近發展區作為問題的著力點

最近發展區是維果斯基的經典理論之一，對教師的教學設計具有指導意義. 以學生認知的最近發展區作為問題的著力點，既讓學生感知問題的挑戰性，又能有效激發學生思考. 學生在自主探究中，抽絲剝繭，獲得探究的成就感，從而形成良性循環.

比如本節課中證明猜想的結論時，教師先降低難度，以推動所有學生參與探究，讓學生以“P，Q為區間A內曲線上的定點”為探究起點，隨著探究的深入，思維拾級而上，新的結論隨著P，Q在曲線上的變化而誕生.

3. 將數學思想方法作為問題的落腳點

數學教學不僅是知識與技能的教學，更是數學思想方法的滲透過程[3]. 數學思想方法是從數學認識中概括、提煉出來的精華，對學習具有重要的幫助. 鑒于此，教師設計問題時，應想方設法挖掘知識背后蘊含的思想方法，并將它們巧妙地融合到學生的探究活動中，引導學生自主體驗、感悟.

總之，以問題驅動探究，促進學生自主建構的教學模式，能有效地彌補傳統教學模式的缺陷，為課堂帶來新的生命力. 但這種教學模式有它自身的特點與應用范圍，并非時時處處可用，不能將這種教學模式代替所有的教學模式. 教學中，教師應根據教學內容與學生的實際情況，選擇搭配教學模式，從真正意義上優化課堂教學，提升學生的數學核心素養.

參考文獻：

[1] ?龐維國.論學生的自主學習[J]. 華東師范大學學報（教育科學版），2001（02）：78-83.

[2] ?史寧中. 數學基本思想18講[M]. 北京：北京師范大學出版社，2016.

[3] ?戴銅. 促進自主學習，體驗成長快樂——基于學生個性化學習的學校文化生態建設[J]. 江蘇教育，2010（32）：51-52.