概率積分預計參數的ENN優化算法

張勁滿 閻躍觀 李杰衛 徐瑞瑞 王芷馨 張 坤 岳彩亞

(1.中國礦業大學(北京)地球科學與測繪工程學院,北京 100083;2.浙江省地質勘查局浙江省地礦建設有限公司,浙江 杭州 310052;3.安徽省煤田地質局,安徽 合肥 230088;4.安徽理工大學空間信息與測繪工程學院,安徽 淮南 232001;5.聊城大學地理與環境學院,山東 聊城 252000)

地下煤炭資源開采后會導致一系列地質災害,如 下沉盆地、塌陷坑及臺階裂縫等,給礦區人民的生產生活和生態環境帶來了一系列危害[1-3]。為了最大限度降低開采沉陷引起的礦區地質災害,以便提前采取合理的防范措施,對煤炭資源采出后引起的地表移動變形進行精準預計顯得尤為重要[4]。概率積分法預計模型作為我國礦山開采沉陷領域應用最為廣泛且較為成熟的方法,近年來不少學者圍繞其預計參數解算精度進行了深入研究[5-9]。賈新果[5]針對開采沉陷參數反演方法存在收斂過早現象采用蟻群算法求解,提高了抗干擾能力和求參精度;張勁滿等[6-7]采用雙參數Knothe時間函數建立了動態下沉模型,模型參數采用最小二乘擬合方法求解,工作面開采沉陷全過程預計精度較可靠;李培現等[8]采用地表空間移動矢量并結合遺傳算法建立了參數反演方法,解決了初值依賴和多工作面難以精確反演的難題。近年來隨著計算機技術快速發展,各種智能優化算法在概率積分參數獲取中得到廣泛應用[10-13]。利用智能優化算法獲取概率積分預計參數具有計算機編程易實現且預測精度高的特點[14-18],其中常用的智能優化方法有BP神經網絡和ENN神經網絡。

BP神經網絡是一種前饋型的網絡,達到全局優化的時間較長且容易陷入局部最優解,ENN網絡比BP神經網絡多了一個記憶層,會使得整個網絡具有更為豐富的動態性和更強的魯棒性,參數預計精度也會得到較大提升。基于此,本研究將蟻群算法(ACO)與ENN神經網絡相結合,提出一種基于ACOENN的概率積分預計參數計算模型,該模型有助于解決ENN神經網絡初始權值與閾值選擇依據不充分的難題,使得模型預測精度更高、可靠性更強。

1 ACO優化ENN神經網絡

1.1 ENN神經網絡

ENN神經網絡是一種前饋式神經網絡,網絡中的延時算子具有記憶功能,使得系統具有較強的適應時變特性的能力,進而具備反映動態過程系統的能力。ENN神經網絡由輸入層、隱含層和輸出層組成,其中隱含層中加入了一個承接層,增強了ENN神經網絡對歷史信息的敏感性,并提高了神經網絡應對突變的能力。ENN神經網絡結構如圖1所示。

圖1 ENN神經網絡結構Fig.1 ENN neural network structure

首先構建ENN神經網格并對其進行訓練,使其具有歷史信息記憶和動態反饋機制,提高ENN神經網絡處理動態信息的能力。ENN神經網絡的數學表達式為

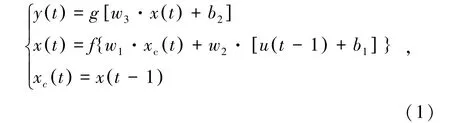
式中,w1為承接層至中間層的連接權值;w2為輸入層至中間層的連接權值;w3為中間層至輸出層的連接權值;u(t-1)為輸入量;b1為輸入層閾值;b2為隱含層閾值;g(·)為輸出神經元的傳遞函數,一般采用purelin函數;f(·)為中間層神經元的傳遞函數,一般采用tansig函數。

ENN神經網絡采用誤差反傳法使得輸出層的實際值與期望值之間的誤差值達到設定的最優值,誤差公式為

式中,yd(t)為第t個節點的實際輸出值;y( t)為第t個節點的期望輸出值。

在ENN神經網絡學習過程中需要不斷地優化權值并獲取最優閾值。一般采用梯度下降算法實現權值尋優,其權值更新公式為

式中,E為誤差函數;η為學習率;ΔW為隱含層權重修正量。

此外,ENN神經網絡閾值尋優一般采用激勵函數實現,其閾值更新公式為

式中,Δb為隱含層閾值修正量;b為閾值。

1.2 ACO算法

ACO是一種模擬生物群體覓食的正反饋、啟發式隨機搜索算法,具有魯棒性好、全局搜索能力強等優點,對非線性問題求解具有較好的適應性。在蟻群算法正反饋作用下,螞蟻選擇路徑的概率表達式為

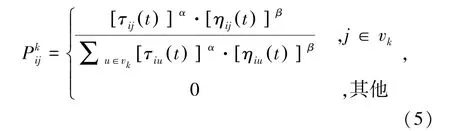
信息素更新在螞蟻尋路過程中起著至關重要的作用,信息素會揮發和疊加,其更新的數學表達式為

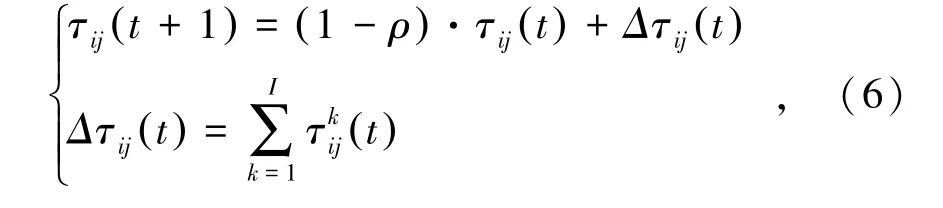
式中,τij(t+1)為t+1時刻位置i至位置j的信息素濃度;Δτij(t)為螞蟻種群I在時間段(t,t+1)位置i至位置j的信息素濃度增加量;ρ為信息素的揮發系數;I為螞蟻種群數;(t)為螞蟻k在t時刻位置i至位置j的信息素濃度。

1.3 ACO-ENN模型構建

本研究采用ACO算法優化ENN神經網絡,構建了ACO-ENN優化模型用于解算概率積分預計參數,流程見圖2。具體步驟為:①確定輸入層、輸出層及隱含層的節點個數,確定ENN神經網絡結構,初始化ENN神經網絡并對網絡參數進行配置;②初始化ACO參數并構造信息素矩陣,利用ACO算法對ENN神經網絡的權值和閾值進行優化,獲取ENN神經網絡的初始權值和閾值。③采用優化后的權值和閾值進行ENN神經網絡學習預測。

圖2 ACO-ENN模型優化流程Fig.2 Optimization flow of ACO-ENN model

2 試驗分析

2.1 試驗數據選取

本研究選取我國典型礦區的30個地表移動觀測站實測資料作為訓練和測試的樣本數據[13],每組樣本數據由地質采礦條件和概率積分預計參數兩部分組成。地質采礦條件包括覆巖堅固系數、采深、采厚、松散層厚度、煤層傾角及采動程度,概率積分預計參數包括下沉系數、水平移動系數、主要影響角正切及拐點偏移距。選取的樣本數據見表1。

表1 實測樣本數據Table 1 Measured sample data

2.2 ACO-ENN模型參數設置

為了精確獲取概率積分預計參數,本研究將地質采礦條件因素作為ACO-ENN模型的輸入節點,即輸入層由6個神經元組成,對應6個影響因素,概率積分預計參數的各個參數分別作為ACO-ENN模型的輸出節點,即輸出層1個神經元,對應概率積分預計參數的各個參數。經過不斷優化訓練可得各個模型的隱含層最優神經元個數分別為:下沉系數網絡模型神經元10個,水平移動系數網絡模型神經元8個,主要影響角正切網絡模型神經元11個,拐點偏移距網絡模型神經元11個。初始種群數為I為30,信息素的揮發系數ρ為0.9,重要程度系數α為0.3,啟發式的重要程度系數β為0.5。

2.3 數據預處理

由于現場觀測環境往往十分復雜,數據采集過程中難免會有一定的誤差,此外,訓練樣本數據和測試樣本數據常存在不同程度的差異性。為降低數據采集誤差和訓練樣本輸入層數據與測試樣本輸入層數據的差異性,在數據訓練之前需要將輸入層的樣本數據進行降噪處理。RW是一種基于加權最小二乘算法對離散數據進行多項式擬合的降噪方法,采用穩健的擬合處理方式以防止偏離點扭曲了平滑的數據點。本研究采用RW方法對實測數據進行降噪處理,降噪后的數據與實測數據對比如圖3所示。

由圖3可知:經過RW降噪處理后數據的上下波動范圍明顯降低,處理后的數據曲線更加平滑。對一些波動范圍較大的數據點進行降噪處理有助于降低數據測量誤差和選擇不合適訓練樣本數據帶來的誤差影響。

圖3 實測樣本數據與RW降噪處理后的結果Fig.3 Measured sample data and results after RW noise reduction processing

2.4 解算結果及分析

將前25組實測樣本數據作為訓練樣本對網絡進行訓練,剩余5組實測樣本數據作為測試樣本。采用ACO-ENN模型對RW降噪處理前后的數據進行訓練并求取概率積分預計參數,實測數據和降噪處理前后ACO-ENN模型預測的概率積分參數如圖4所示。由圖4可知:采用RW方法預先進行了預處理后,再進行ACO-ENN預測,獲取的概率積分參數預計值精度優于ACO-ENN模型預計值,反映出采用RW法對原始樣本數據進行預處理有助于提高數據質量。

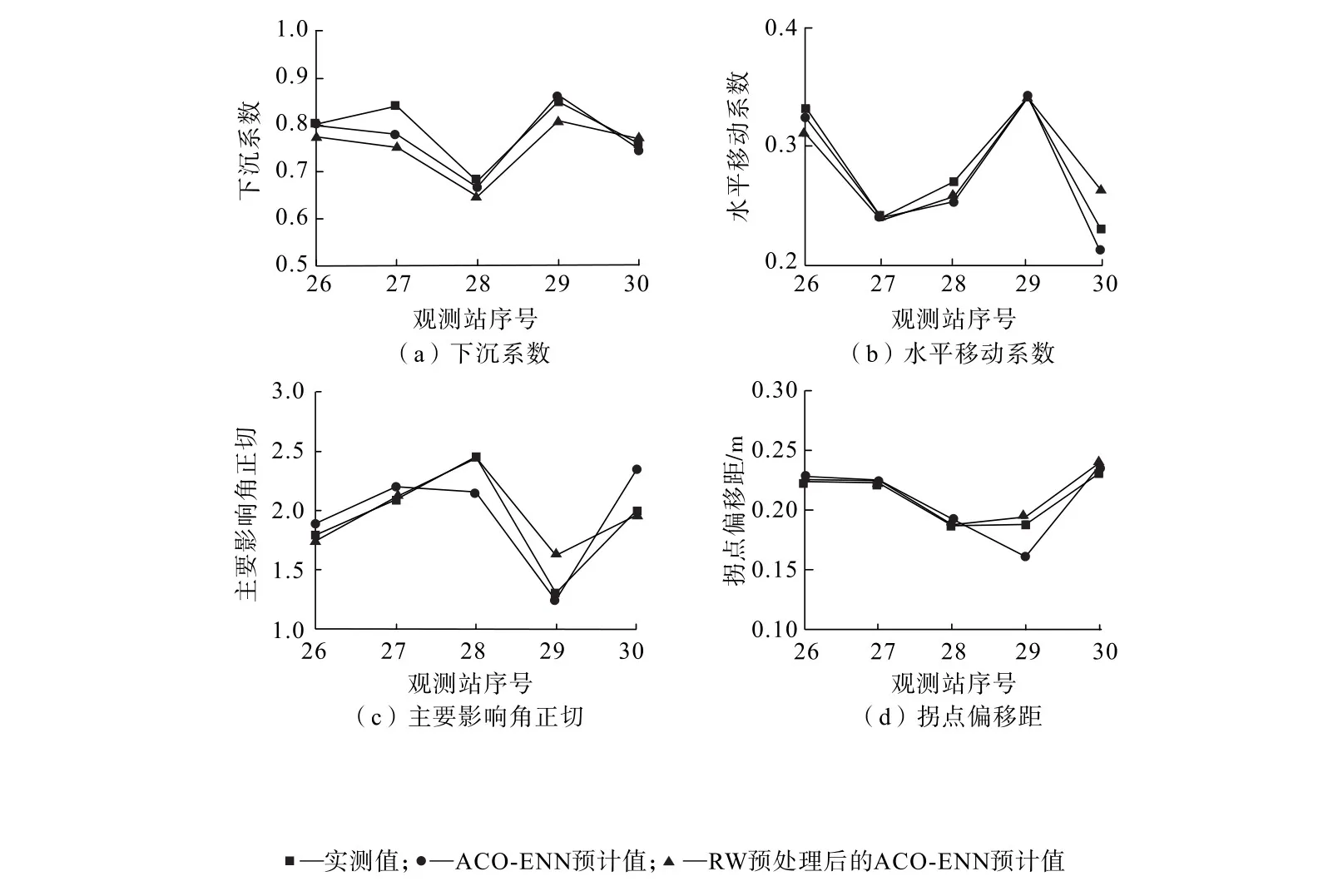
圖4 概率積分參數預測值與實測值對比Fig.4 Comparison of the predicted and measured values of expected parameters

基于RW方法進行降噪預處理后的樣本數據分別采用ACO-ENN模型和傳統的ENN神經網絡對下沉系數、水平移動系數、主要影響角正切和拐點偏移距進行預測,預測結果如圖5所示。由圖5可知:在下沉系數和水平移動系數預測過程中ACO-ENN模型的預測精度優于ENN神經網絡,可靠性更強,在主要影響角正切和拐點偏移距的預測過程中ACO-ENN模型的預測誤差絕對值整體小于ENN神經網絡,預測精度較高。概率積分各預計參數的平均預測相對誤差和均方根誤差見表2。由表2可知:利用ACOENN模型解算下沉系數、水平移動系數、主要影響角正切及拐點偏移距的平均相對誤差分別為2.41%、3.48%、6.11%和1.67%,ACO-ENN模型解算結果的平均相對誤差和均方根誤差均優于傳統ENN神經網絡,表明ACO-ENN模型解算精度更高、可靠性更強。

圖5 概率積分法預計參數絕對值誤差Fig.5 Absolute value error of parameters expected by probability integration method

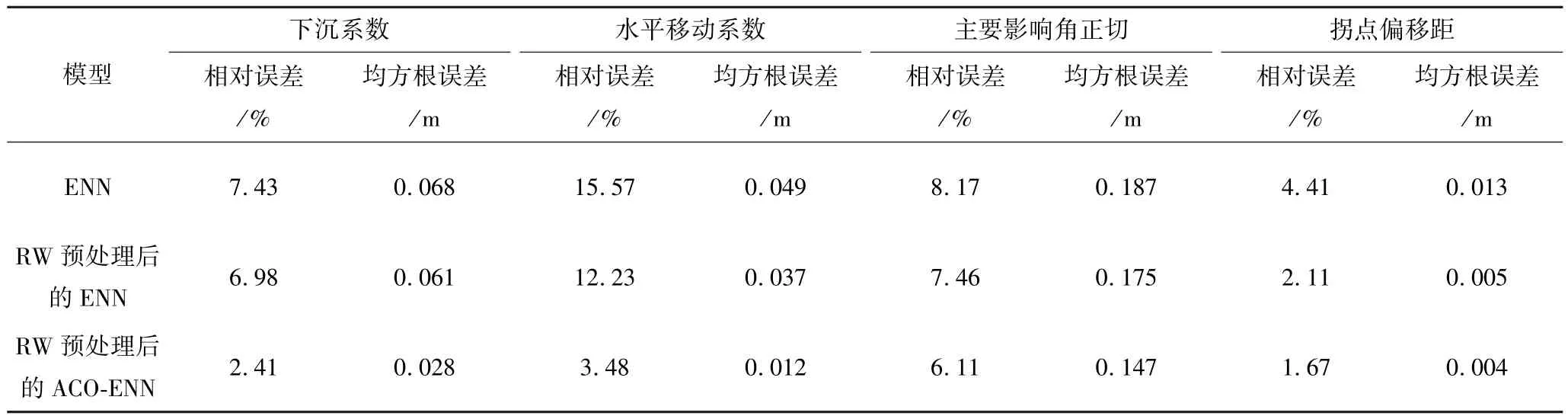
表2 各模型預測結果精度對比Table 2 Comparison of the accuracy of prediction results by models

3 結 論

(1)針對傳統ENN神經網絡初始權重與閾值選擇缺乏依據的不足,采用ACO算法對ENN神經網絡的權值和閾值進行優化,優化后ENN神經網絡輸入層數據采用RW進行預處理,建立了ACO-ENN概率積分預計參數解算模型。

(2)利用ACO-ENN模型分別學習經過RW降噪處理和未經RW降噪處理的實測樣本數據,解算結果表明:RW降噪處理顯著提高了ACO-ENN模型輸入層的數據質量;利用ACO-ENN模型和ENN神經網絡分別解算經過RW處理的樣本數據,表明ACO-ENN模型解算精度明顯優于ENN神經網絡。

(3)ACO-ENN模型求取的下沉系數、水平移動系數及拐點偏移距平均相對誤差偏差較小,但主要影響角正切的平均相對誤差偏差較大,基于ACO-ENN模型構建概率積分預計參數的組合解算模型是下一步研究方向。