不同類型生態護坡在灌區渠道應用的多屬性決策模型

肖合偉 裴文杰 謝高鵬

（江西省潦河工程管理局 宜春 330700）

在灌區開展渠道護坡建設的意義主要包括兩方面：一是保護河道沿岸邊坡，防止流水沖擊、毀壞邊坡；二是防止水滲入，降低水資源利用率。長期以來，灌區渠道普遍采用硬質化護坡技術，雖然有效地提高了邊坡安全性和水資源利用率，但是同時也嚴重破壞了原有河岸生態轉換、生物棲息地和綠色景觀等功能。為了協調邊坡安全、防滲、景觀和生境條件等多方面，近年來生態護坡的概念被提出，并且得到了國內外普遍認可和廣泛推行。本文基于多目標決策理論提出不同類型生態護坡在灌區渠道應用的多屬性決策模型，以期為今后灌區渠道生態護坡建設工作提供借鑒參考。

1 生態護坡選擇問題的數學概化

生態護坡選擇問題可以概化成渠道、生態護坡兩個集合中的個體根據相互間的適宜程度進行優化配置。決策者一方面需要考慮生態護坡與渠道的適宜程度，另一方面考慮在該渠道實施生態護坡后的效益，此外還需考慮實施的成本。

令 I={1,2,…,m}，J={1,2,…,n}，（m ≥ 2，n ≥2）。設有灌區渠道集合，記作A={A1,A2,…,Am}，其中Ai為灌區渠道集合A 中第i 條渠道，i ∈I；設有生態護坡集，記作B={B1,B2,…,Bn}，其中Bj為B中第j 項生態護坡技術，j ∈J。

就對渠道Ai而言，生態護坡技術Bj的效益為rij∈S，S=[smin,smax]，其中smin、smax分別為對渠道而言，生態護坡效益的上、下限。此處效益通過生態護坡評價指標表征。灌區渠道A 關于生態護坡B 的效益矩陣為R=[rij]m×n。同理，就生態護坡集而言，每一項生態護坡技術對應每一條渠道也有一個應用的適宜程度，就生態護坡技術B 對灌區渠道A 的適宜度Bj矩陣為T=[tij]m×n，其中tij表示生態護坡技術對渠道Aj的適宜程度。

需要指出的是：生態護坡選擇問題是灌區渠道與生態護坡技術之間的多對多匹配（m-n），可以將集合中的渠道或生態護坡技術視作多個具有相同屬性的個體，這樣就可以將多對多的匹配問題（m-n）轉化成一對一（1-1）匹配，轉化后的匹配問題的描述與計算將更加簡便。

2 滿意度、適宜度、成本矩陣的構造

本文采用將生態護坡措施實施效益與實施適宜程度進行排序和歸一化處理，轉化為滿意度與適宜度，再進行排序的處理方式，這樣處理的目的是：一是消除量綱不一致的情況；二是相同指標在不同渠道上的敏感程度可能存在較大差別，導致生態護坡匹配模型失效；三是為了描述和計算的簡便，可以將集合中的渠道或生態護坡技術視作多個具有相同屬性的個體，將多對多的動力匹配問題（m-n）轉化成一對一（1-1）匹配，假設渠道2、渠道3（A2、A3）采用生態護坡技術B2 時的效益分別為6 和8，并且是渠道A2、A3 在諸多生態護坡技術中的最高，那么渠道A2、A3 對生態護坡技術B2 應該具有同等的匹配效力，進行動力需求滿足排序計算可以實現。

在生態護坡選擇匹配決策問題中，不失一般性，若渠道Ai將生態護坡技術Bj排在第1 位，那么記排序ai,j=1，渠道Ai對生態護坡技術Bj滿意程度最高；渠道Ai將生態護坡技術Bk排在最末，那么記排序ai,k=n，渠道Ai對生態護坡技術Bk滿意程度最低。此處的滿意程度與適宜程度含義相似，采用如下公式計算渠道對生態護坡技術的滿意度αi,j、生態護坡技術對渠道的適宜度βi,j：

在實際工程應用中，決策者除了需要考慮生態護坡技術實施的效用與適宜程度，還需實施的成本，在綜合考慮生態護坡技術能夠取得的效益與需要投入的成本的基礎上，作出最優決策。設對渠道Ai實施生態護坡技術Bj的成本為ci,j，那么實施生態護坡技術的成本矩陣C 可以表示為：

考慮到下文需將生態護坡選擇多目標優化模型轉化求解，對重構措施成本也進行線性歸一化，計算公式如下：

3 生態護坡選擇多目標優化模型

3.1 目標函數

基于上文提出的渠道與生態護坡技術的滿意度、適宜度、生態護坡技術實施成本等的定義與描述，可將生態護坡選擇問題轉化成如下多目標優化模型：

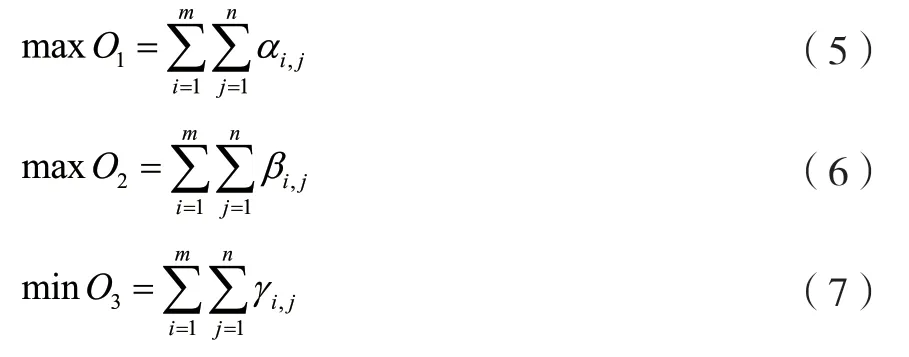
3.2 約束條件

生態護坡選擇多目標優化模型的約束條件包括水量平衡約束、水位約束、流量約束、流速約束、水質約束、水質平衡約束、工程運行約束等。

3.2.1 水量平衡約束

灌區系統中，各單元需要遵循水量平衡約束，表達為下式所示：

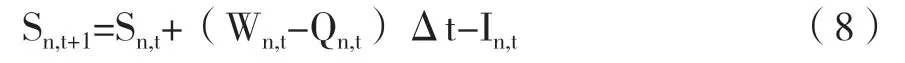
式中：Wn,t為第n 個單元t 時段內的入流量；Qn,t為第n 個單元t 時段內的出流量；Sn,t+1為第n 個單元t 時段末的蓄水量；Sn,t為第n 個單元t 時段初的蓄水量；In,t為第n 個單元t 時段內的損失水量；Δt 為計算時段區間。

3.2.2 水位約束

灌區系統中，渠道等單元的水位在不同時期均需滿足特定最低限和最高限要求，以滿足防洪、供水、生態等需要，表達為下式所示：

式中：Zn,t為第n 個單元t 時段的水位；Zn,t,min為第n 個單元t 時段允許最低水位；Zn,t,max為第n 個單元t 時段允許最低水位。

3.2.3 流量約束

除水位約束外，渠道單元在不同時段也有相應流量、流速要求，一般與調度規則、工程特性等因素相關，表達為：

式中：Qn,t為第n 個單元t 時段的流量；Qn,t,min為第n 個單元t 時段允許的最小流量；Qn,t,max為第n個單元t 時段允許的最大流量。

3.2.4 流速約束

式中：Vn,t為第n 個單元t 時段的流速；Vn,t,min為第n 個單元t 時段允許的最小流速；Vn,t,max為第n個單元t 時段允許的最大流速。

3.2.5 水質約束

式中：qn,t為第n 個單元t 時段水質指標；qn,t,max為第n 個單元t 時段最低水質目標。

3.2.6 工程運行約束

主要包括灌區系統中諸多水利工程的過水能力、調度運行方式約束等。

3.3 模型求解

考慮到αi,j、βi,j、γi,j均為歸一化值，因此可采用線性加權法動力匹配多目標優化模型轉化為如下單目標優化模型求解：

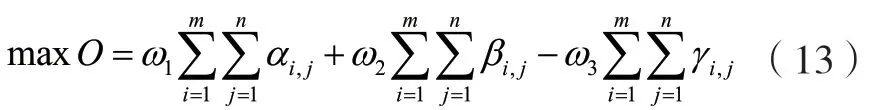
在上述綜合目標函數中，ω1、ω2、ω3為各分目標的權重系數，反映實際情況下各目標的重要程度，可依據實際問題給定，也可采用主觀賦權法（如層次分析法）或客觀賦權法（如熵權法）或者主客觀相結合的方法確定。

轉化后的模型求解可采用粒子群算法等求解方法或使用LINGO 軟件求解。

4 結語

生態護坡技術在基本的保護邊坡、提高水資源利用率功能的要求上，構筑能透水透氣、生長植物的生態型護坡，強調安全性、穩定性、景觀性、生態性、自然性和親水性的協同。本文提出的不同類型生態護坡在灌區渠道應用的多屬性決策模型可為今后灌區渠道生態護坡建設工作提供決策支持■