基于混合聚類算法的大學生心理健康分析

馬曉巖

（中國人民解放軍93897 部隊保障部衛生隊，陜西 西安 710000）

隨著社會的發展及教育資源的不斷優厚，當今時代大學生越來越多元化，學生的需求也發生了很大變化。大學生的心理健康問題不僅越來越復雜，而且數量越來越多、嚴重程度也越來越高[1-2]。

為此，許多學者將機器學習用于心理醫療診斷領域[3-4]。楊昱梅[5]等基于數據挖掘理論對大學生心理健康狀況進行了分析和研究。楊帆[6]等利用兩步聚類和快速聚類兩種聚類分析方法對青少年危險行為進行聚類分析，并據此為青少年制訂干預方案。聶敏等[7]研究了高校學生心理健康情況對其社交網絡結構的影響，挖掘學生的抑郁癥狀發生水平。Kesuma Z M[8]等利用中值聚類算法對孕產婦心理保健服務進行聚類分析。

上述研究大都采用有監督的機器學習方法來學習模型，其中可以使用標記良好的數據樣本。然而，對于心理健康領域存在不足，特別是許多心理健康前期無明顯表征，或者其特征是不確定或短暫的狀態。因此，在該文研究中，假設在那些有極端心理健康問題與正常健康狀態之間存在一些中間階段，并提出了K-means 結合蟻獅優化算法對學生進行聚類劃分，進一步幫助了解大學生心理健康階段，為大學生心理輔導或心理干預提供參考。

1 相關概念

1.1 K-means聚類分析算法

聚類[9-11]是基于某種相似性度量對一組對象進行分組的過程。每一組分區對象都稱為一個集群。分區是通過聚類算法來完成的。因此，聚類是有利的，因為它可以在相同的數據中獲得先前未知的組。數據聚類是發現數據集中結構的有效方法。一些聚類方法將對象劃分為簇之間沒有特定的邊界，而其他一些方法則將對象劃分為互斥的簇。同時，也有一些方法把兩個物體之間的距離作為相似度的標準。

K-means 聚類[12-13]是一種無監督的硬劃分聚類方法。目標是目標函數J，從數據中找到k個聚類，具體定義如下：

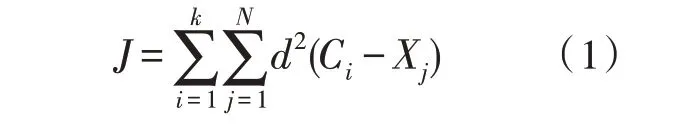
其中，d2(Ci-Xj)是第i個簇質心和第j個數據點之間的歐式距離的平方。N是數據點的總數。根據得到的距離，將點分配給距離質心最小的簇。在對這些點進行聚類后，找到屬于該聚類的所有點的平均值。然后將平均值指定為下一次迭代的新的聚類質心。重復這個過程，直到得到的質心與上一次迭代的質心相同。K-means 算法的目標是最小化目標函數。

1.2 蟻獅優化模型

蟻獅優化模型[14-15]是一種自然啟發的算法，它遵循螞蟻幼蟲的捕食行為。一只蟻獅幼蟲在沙子里沿著一條環形的路徑移動，用它巨大的顎把沙子扔出去，從而形成一個圓錐形的洞。挖完陷阱后，幼蟲躲在圓錐體的底部，等待螞蟻被困在坑里。一旦蟻獅意識到獵物被困住了，它就會把沙子向外扔，并把獵物滑進坑里。當獵物被抓進下巴時，蟻獅會把獵物拉向自己并吃掉。這個過程在數學上被設計用來執行優化。該方法主要有5 個步驟如下：

1）螞蟻的隨機游動；

2）建立陷阱；

3）將螞蟻困在陷阱中；

4）捕捉獵物；

5）重建陷阱。

螞蟻利用隨機游動在受螞蟻陷阱影響的搜索空間中移動。在每次迭代中，螞蟻的位置都會隨著隨機游動而更新。迭代t的隨機游動由如下公式獲取：

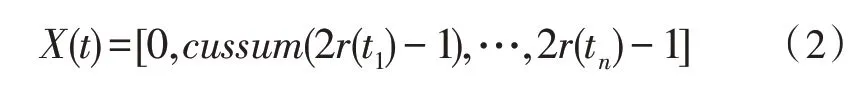
其中，X(t) 為螞蟻隨機游動時步數的集合。cussum為計算過程中的累加和。t為迭代過程中的步長，r(t)為隨機函數，具體定義如下：

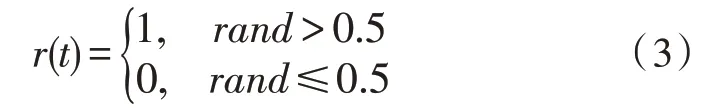
為了確保所有隨機游動都在搜索空間的邊界內，使用如下所示的歸一化公式：

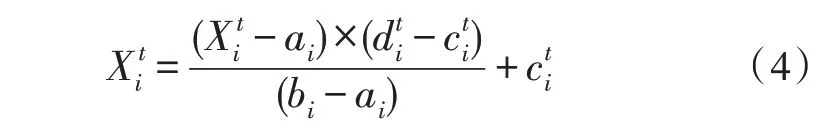
其中，ai、bi分別為第i維變量隨機游動的最大值和最小值。分別為第i維變量在迭代t時的最小值和最大值。

此外，螞蟻制造的陷阱將會對其隨機行走產生影響，為此建立如下模型：

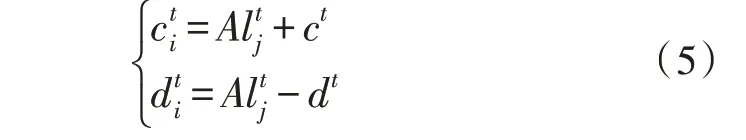
其中，ct、dt分別為所有變量的最小值和最大值，為第j只螞蟻在迭代t時的位置。

進一步采用輪盤賭選擇方法，根據螞蟻的適應度值進行優化。在每次迭代中將最適合的螞蟻保存為精英螞蟻。精英將影響螞蟻的整體運動。此外，螞蟻的位置會根據所選螞蟻和精英的隨機游動來更新。每只螞蟻都會繞著一只選定的螞蟻游走，因此也可能會圍繞精英游走。該過程可描述為：

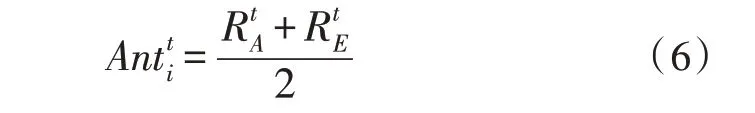
其中，為螞蟻利用輪盤賭在迭代值為t時到蟻獅周圍隨機游動l步時的值。為螞蟻在迭代t時到精英蟻獅周圍隨機游動l步時的值。

此外，計算所有螞蟻的適應值。如果一只螞蟻比剩余螞蟻有更好的適應能力，則其被相應的螞蟻取代。同樣地，如果任何一個蟻獅比精英蟻獅更優，則精英蟻獅也會被該蟻獅取代。

2 改進的混合聚類分析算法

該節將介紹一種改進的混合聚類分析算法，為幫助了解大學生心理健康階段，為大學生心理輔導或心理干預提供參考。該算法是由K-means 和蟻獅優化算法混合而成。

2.1 算法執行過程

首先，確定要形成的簇的數目。然后根據得到的最小歐氏距離對所有數據點進行聚類。然后，為得到的每個簇計算優化的簇質心。在優化過程中，每個簇隨機初始化為螞蟻和螞蟻種群。然后利用K-means 聚類方法的目標函數，計算所有螞蟻和螞蟻的適應度值。當簇內距離的平均值之和最小時，將適應度值最小的蟻群作為精英值。之后對每一個簇進行蟻獅優化，得到簇質心的最佳位置。K-means聚類算法將返回的精英作為質心。該方法的流程如圖1 所示。

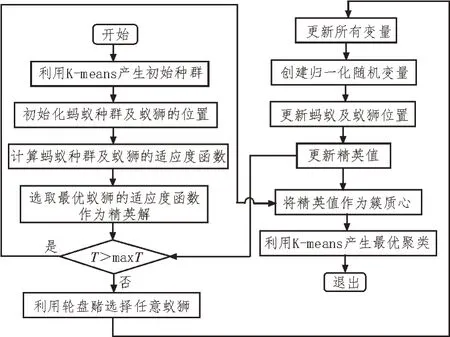
圖1 改進的混合聚類分析算法執行流程

2.2 算法性能指標

為驗證算法性能，基于不同的性能指標對算法的聚類質量進行了評價。文中引入的性能指標是群內距離平均值和F測度。

2.2.1 群內平均距離

聚類的原則是屬于同一簇的數據點應盡可能靠近，即簇內距離應盡可能小，以獲得最優的聚類質量。

常用計算簇內距離[16]的方法有歐式距離d、曼哈頓距離d12和余弦相似度dc等，距離計算公式如下：

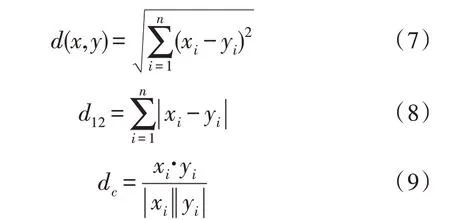
其中，xi、yi為簇內任意兩個點的值，n為簇內點的數目。

2.2.2 F測度

利用信息檢索[17]中準確率和召回率的概念計算F測度。數據集的每個聚類i記為查詢所需的ni項集，每個聚類j記為一個查詢檢索到的一組nj項。故nij表示聚類j中第i類的元素數量。因此，準確度pre、召回率re和F測度的計算公式如下：

3 實驗分析

為分析大學生的壓力和健康相關行為，以一個實際案例驗證所提方法。首先，數據集由問卷調查方式通過統計參與者在近兩個月內的情況生成，每個問題分為有1～5 分5 個等級。表1 所示為調查結果部分統計情況。

表1 部分心理測試試題

3.1 算法性能測試

利用文中所提方法對數據集進行聚類分析。圖2 所示為578 名學生心理健康聚類結果，其中橫軸表示聚類劃分的不同層級，包括正常、輕微、中等、嚴重和特別嚴重5 個級別。可以看出調查結果中49.6%的人有輕度或更高的抑郁癥狀，60.0%的人有焦慮癥狀，42.0%的人有精神壓力。

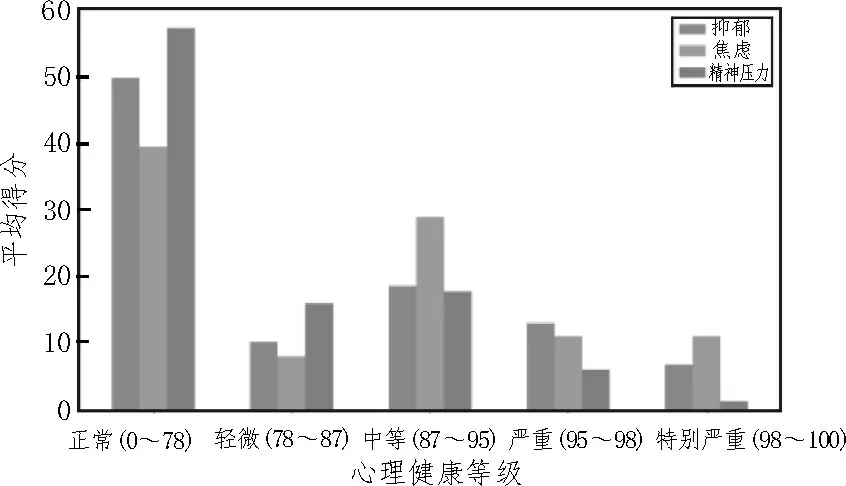
圖2 心理健康聚類結果

將文中算法的聚類結果歸一化后與傳統K-means、K-means PSO、K-means FA、模糊K-means 相比，聚類結果的群內平均距離和F測度如表2 所示。可以看出，K-means PSO 和文中方法提供了最小的簇內距離。隨著迭代次數的增加，模糊K-means 和文中算法比較穩定不會出現波動現象。綜合比較，文中方法比其他方法結果更好。

表2 不同算法性能對比結果

3.2 算法差異性測試

為了確定聚類算法之間是否存在顯著的性能差異，將測試者分為4 組進行統計分析。為了確定差異，文中采用了Friedman 檢驗[18]。Friedman 檢驗是一種非參數檢驗，用于找出順序因變量組間的差異。零假設用H0描述所有聚類算法的性能相同。

試驗的置信水平α取0.1。對于每組數據，所有算法都進行了相應的排序計算，故j個算法的平均排序Rj計算如下：

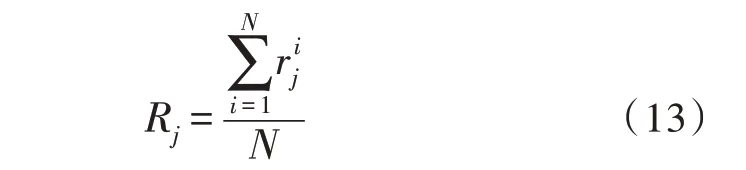
其中，N為測試次數，為第j個算法在第i（i∈[1,N]）次測試中的排序。表3 所示為不同算法在測試中的排序統計結果。可以看出文中方法表現最好，K-means 方法表現最差。

表3 不同算法排序統計結果

Friedman 檢驗計算公式如下：

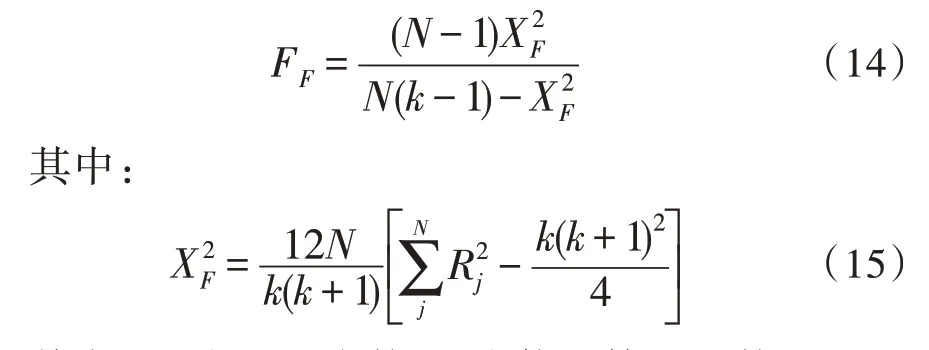
其中，N為測試次數；k為使用算法的數量。

Friedman 統計量FF由自由度為k-1 和(k-1)(N-1)的F分布構成。對于5 個算法和8 個數據集，自由度在4～28 之間。Friedman 檢驗中z值計算公式如下：

然后，利用z值得到概率p與α/(k-1)。表4 為不同算法的Friedman 檢驗統計結果。

表4 Friedman檢驗統計結果

由表4 可知，無效假設被拒絕。因此各算法性能不同。綜合以上分析結果，可以確定文中所提方法在統計上比K-means、K-means PSO、K-means FA、模糊K-means 算法表現更好。

4 結論

文中對大學生心理健康的聚類分析問題進行了研究，提出了應用于大學生心理健康程度的聚類分析模型，并實現了一種混合聚類優化算法。

文中在模型驗證時選取的數據類型較為基礎，仍存在進一步提升空間。同時對數據整合時僅為統計學分析，沒有進行數據挖掘與內部關系探討。未來研究的方向包括數據校驗，挖掘各指標之間內涵關系等。