振動慢剪破碎機內錐動力學分析

蔡改貧，郝書灝，黃金若，胡 振

(江西理工大學 a. 機電工程學院；b. 江西省礦冶機電工程技術研究中心，江西 贛州 341000)

近年來，隨著科學技術的不斷發展，能源的消耗持續增加，國內外研究人員對充分利用能源和節能降耗的課題進行了深入的研究[1-3]。在礦業生產活動中，礦產資源主要是通過破碎以及研磨之后才能得到充分的利用，所以研究礦產資源的破碎是實現能源充分利用和節能降耗的根本任務之一[4-8]。振動慢剪破碎機作為一種礦石破碎設備具有非常重要的研究意義以及研究價值，如何在提高破碎機工作效率的同時降低能耗是當前重要的研究課題[9-10]。

由于振動慢剪破碎機的破碎力主要是外錐在做繞整機中心軸線的旋轉運動以及內錐在做振動時產生的沖擊運動所提供的，外錐的圓周運動較為簡單，內錐的振動運行形式較為復雜，所以本文中主要針對振動慢剪破碎機內錐的動力學進行研究，主要是對內錐的動力學模型進行建模分析，對內錐的動力學響應進行分析，利用機械系統動力學自動分析軟件(automatic dynamic analysis of mechanical systems, ADAMS)進行空載下的動力學響應仿真分析和利用工程離散元分析(EDEM)與ADAMS耦合進行負載下的動力學響應仿真分析。

1 振動慢剪破碎機工作原理

振動慢剪破碎機是本課題組研發的一種新型細碎的礦石破碎設備，其結構簡圖如圖1所示。振動慢剪破碎機外錐在外錐齒輪的帶動下做繞整機中心軸線的旋轉運動，內錐在立式激振器的帶動下做振動運動，利用外錐以及內錐運動所提供的破碎力，對礦石進行剪切、擠壓、沖擊、劈裂，從而實現礦石的細碎。該振動慢剪破碎機具有細碎效果好、破碎產品粒度均勻、處理量大等優點，可以高效完成細碎礦石作業[11]。

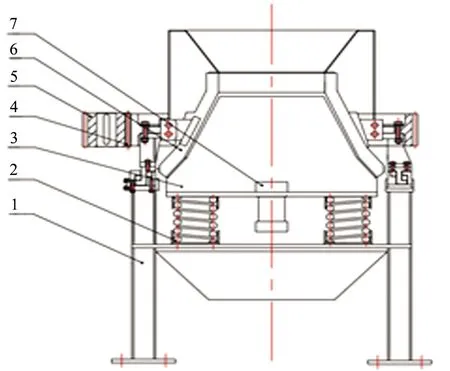
1—機架；2—主振彈簧；3—破碎機內錐；4—破碎機外錐齒輪；5—傳動齒輪；6—破碎機外錐；7—立式激振器。

2 振動慢剪破碎機內錐動力學模型

振動慢剪破碎機內錐的振動運動是一種非線性多自由度的振動系統，其運動形式十分復雜。內錐做空間自由運動，即在X、Y、Z方向的平動以及繞X、Y、Z方向的轉動，共有6個自由度r。通過分析，振動慢剪破碎機內錐簡化力學模型如圖2所示，其中，m0是偏心塊質量，m1是內錐質量，k是主振彈簧剛度，x、y、z為3個方向上的位移，α、β、γ為X、Y、Z方向上的轉動角度。

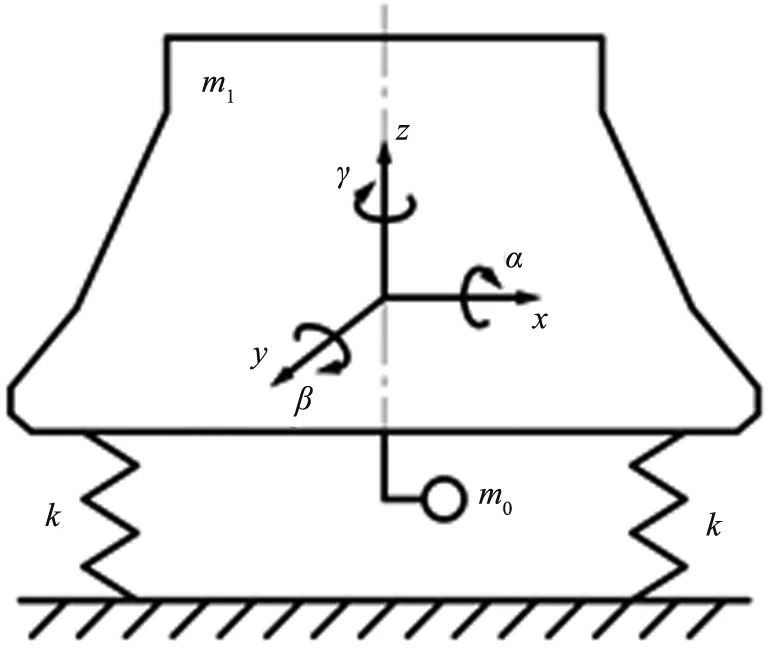
圖2 振動慢剪破碎機內錐簡化力學模型

利用拉格朗日方程建立振動慢剪破碎機內錐動力學方程[12-13]，該系統的振動方程可由動能、勢能等來表示，即

(1)

式中：Qr為對第r個廣義坐標的廣義力，N；t為時間，s；E為系統的動能，J；qr為第r個自由度的廣義坐標；U為系統的勢能，J。

2.1 系統的動能

系統的動能由偏心塊的動能以及內錐動能組成，其表達式為

(2)

其中

ωx=α′cosβcosγ+β′ sinγ,

(3)

ωy=-α′ cosβsinγ+β′ cosγ,

(4)

ωz=α′ sinβ+γ′,

(5)

式中：Em0為偏心塊的動能，J；Em1為內錐的動能，J；i為0,1;x0、y0、z0為偏心塊在X、Y、Z方向的位移，m；x1、y1、z1為內錐在X、Y、Z方向的位移，m；j為0，1；Ix0、Iy0、Iz0為偏心塊在X、Y、Z方向的轉動慣量, kg·m2；Ix1，Iy1，Iy1為內錐在X、Y、Z方向的轉動慣量，kg·m2;j為0，1；ωx、ωy、ωz為內錐和偏心塊在X、Y、Z方向的角速度，rad/s；α、β、γ為X、Y、Z方向上的轉動角度, rad/s。

由于偏心塊的動能計算十分復雜，因此本文中采用坐標變換求解其位置，然后進行求導得到其速度，再計算偏心塊動能。偏心塊安裝在內錐上，其運動后的絕對坐標為

(6)

式中：e為偏心塊的偏心距, m；ω為偏心塊的角速度, rad/s。

2.2 系統的勢能

系統的勢能由彈簧的變形勢能組成，其計算表達式為

(7)

其中

(8)

(9)

(10)

式中：Uk為彈簧的勢能，J；kx、ky、kz為彈簧在X、Y、Z方向的剛度，N/m；xk1、yk1、zk1為在X、Y、Z方向的變形后的坐標, m；xk、yk、zk為在X、Y、Z方向的變形前的坐標, m。

系統的總勢能表達式為

(11)

2.3 振動微分方程

系統的廣義干擾力為系統中的非理想約束的反力，即阻尼。將前文求得的系統動能、勢能以及廣義干擾力代入拉格朗日方程式(1)中，可以建立振動慢剪破碎機內錐6個自由度振動微分非線性方程組，通過進行相應的簡化以及線性化處理[14-15]，得到內錐六自由度振動微分方程組：

(12)

2.4 振動慢剪破碎機內錐動力學響應

結合自制的實驗樣機，可以得到振動慢剪破碎機系統參數，如表1。根據所建立的破碎機空載狀態下內錐的六自由度振動微分方程組，利用MATLAB(矩陣實驗室)數學分析軟件求解可以得到系統在平面上的動力學響應，內錐質心的平面運動計算軌跡如圖3。結合圖分析可知，內錐在X、Y方向上的位移范圍為-0.6～0.6 mm，整體振幅為1.2 mm，振動慢剪內錐的運動主要為水平面上的振動圓運動，其運動軌跡整體呈現一定的規律性，是一種非線性概周期運動。

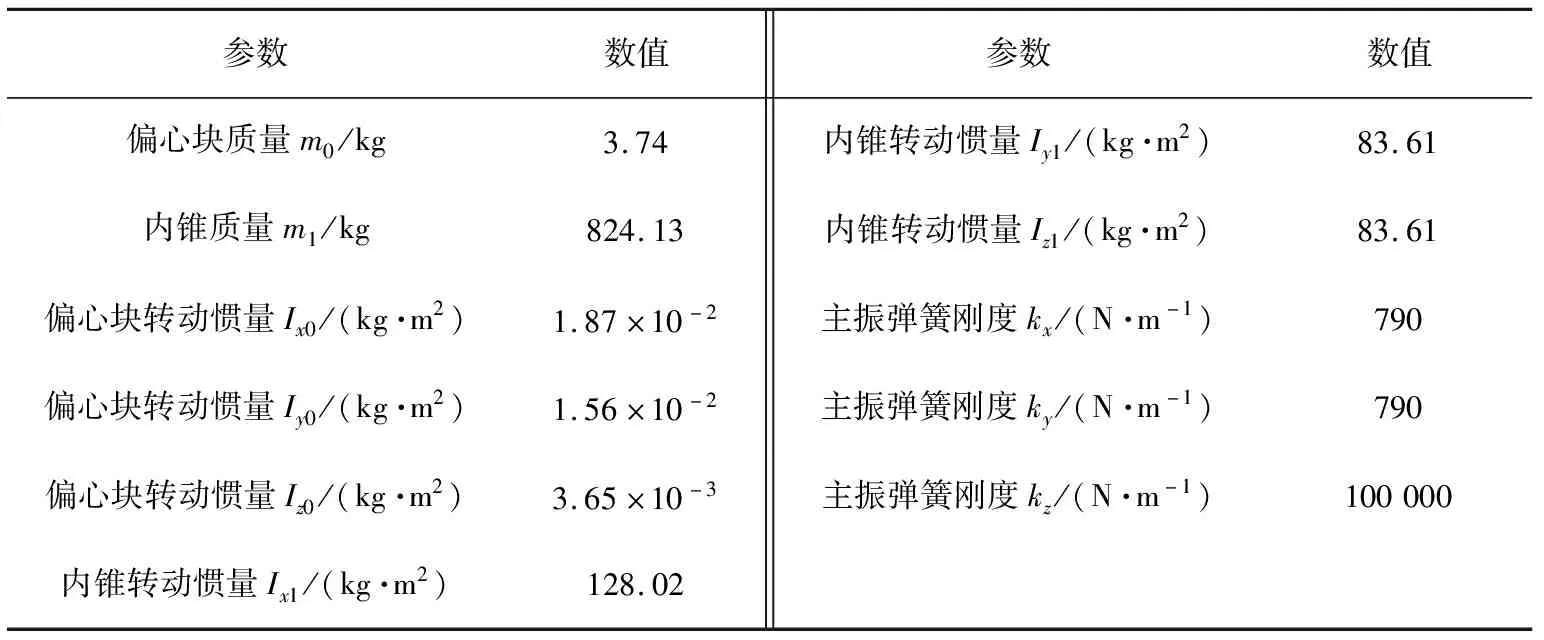
表1 振動慢剪破碎機系統參數

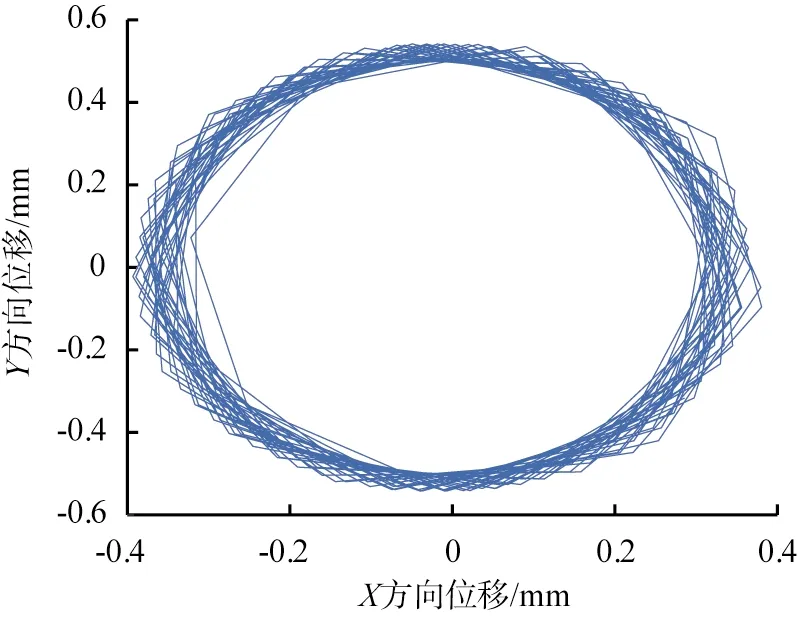
圖3 內錐質心的平面運動計算軌跡

3 內錐運動仿真分析

3.1 內錐虛擬樣機模型的建立

在UG中建立振動慢剪破碎機內錐、內錐底盤、振動電機主體、偏心塊等三維幾何模型，同時按照實際位置進行裝配，內錐虛擬樣機三維幾何模型如圖4所示。在UG中將裝配體以Parasolid格式將模型導入到運動學分析軟件ADAMS中，按照樣機實際情況添加各部件的材料屬性；根據振動慢剪破碎機實際約束情況，添加連接關系，其中內錐與內錐底盤之間為固定連接，內錐底盤與振動電機主體之間為固定連接，振動電機主體與偏心塊之間為旋轉連接；在振動電機主體與偏心塊之間施加電動機驅動，其驅動函數為STEP(time, 0, 0, 6, 1 450×2×PI)+STEP(time, 16, 0, 18,-1 450×2×PI)，代表在0～6 s時偏心塊轉速由0增加為1 450 r/min，在6～16 s時偏心塊穩定運行轉速為1 450 r/min，在16～18 s時偏心塊轉速由1 450 r/min降低為0；添加內錐底盤與機架(大地)之間的彈簧模型，傳統彈簧模型僅有軸向運動，不能滿足實際需要，所以為滿足內錐底盤與機架之間的彈簧實際要求，本文中采用ADAMS中的Bushing，其可以提供6個方向上的剛度與阻尼。建立的振動慢剪破碎機內錐虛擬樣機裝配模型，如圖5所示。

圖4 內錐虛擬樣機三維幾何模型Fig.4 3Dgeometricmodelofinnerconevirtualprototype圖5 內錐虛擬樣機裝配模型Fig.5 Assemblymodelofinnerconevirtualprototype

3.2 內錐運動狀態仿真及結果分析

在虛擬樣機模型中，在內錐質心位置上標記一個MARKER點，以該點的運動軌跡來描述內錐運動狀態。仿真完成后，在后處理中可以查看仿真結果，將仿真數據導出，經過MATLAB軟件分析可以得到該MARKER點的平面的位移圖像，內錐質心的平面運動軌跡如圖6所示。

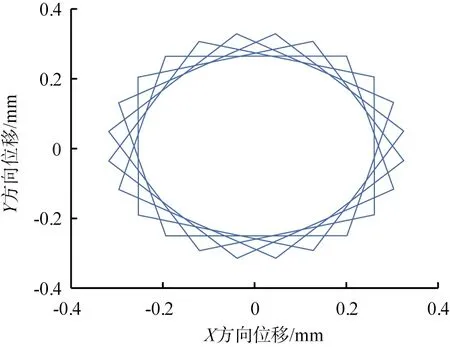
圖6 空載時內錐質心的平面運動軌跡

分析圖6可知，其仿真結果與建立的振動慢剪破碎機動力學模型所求的動力學響應結果一致，其內錐的主要運動為水平面上的振動圓運動，內錐在X、Y方向上的位移范圍為-0.4～0.4 mm，整體振幅為0.8 mm。

4 破碎仿真試驗

4.1 基于EDEM與ADAMS的破碎仿真模型

為探究振動慢剪破碎機在負載情況下的內錐運動情況，將EDEM與ADAMS進行耦合仿真[16]。將UG中建立的振動慢剪破碎機三維模型分別導入到EDEM與ADAMS，利用ADAMS Co-simulation實現2款軟件的耦合仿真，其中EDEM提供顆粒信息，ADAMS提供運動信息。

ADAMS中主要的設置過程已在3.1節進行介紹，EDEM中按照實際情況選擇入料粒徑為35～45 mm，破碎模型選擇Tavares破碎模型[17-18]，表2為鎢礦石顆粒與內、外錐的材料參數。

表2 材料參數

4.2 破碎仿真結果的分析

在EDEM后處理中的破碎仿真效果如圖7所示，由圖可知，礦石顆粒呈分層破碎，上部顆粒粒徑較大，進入排料口區域的礦石顆粒較小，其中入料粒徑為30～45 mm、排料粒徑為0.36～18 mm，與實際破碎過程相符。

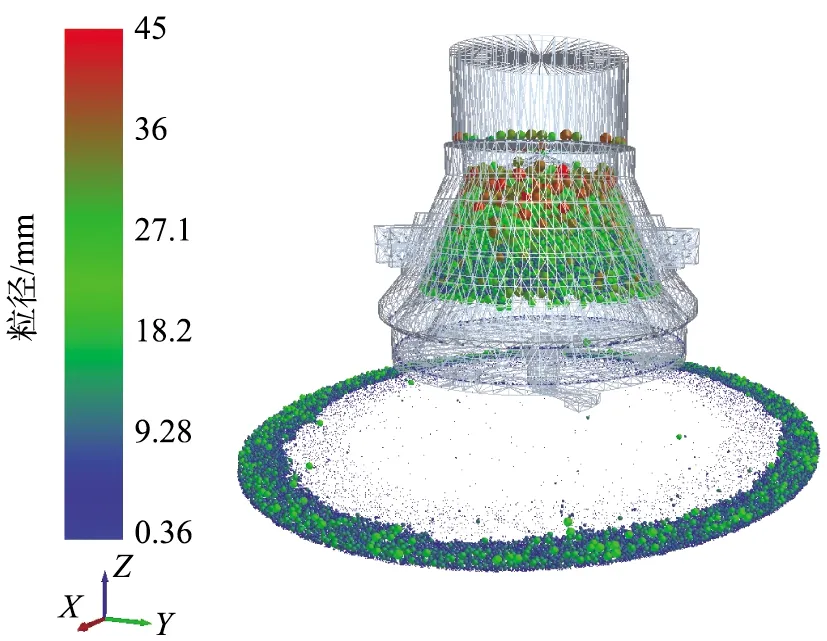
圖7 EDEM中破碎仿真效果

為探究振動慢剪破碎機在負載情況下的內錐運動情況，將破碎模擬結果通過ADAMS導出內錐質心MARKER點的X、Y方向位移數據，通過MATLAB數學處理軟件，繪制內錐負載情況下在平面內的運動軌跡，如圖8所示。分析圖8可知，其內錐的主要運動為水平面上的振動圓運動，同時在負載的作用下，內錐在X、Y方向上的位移范圍為-0.3～0.3 mm，整體振幅為0.6 mm，與空載情況下的X、Y方向上的位移范圍為-0.4～0.4 mm，整體振幅為0.8 mm相比，振幅減小。

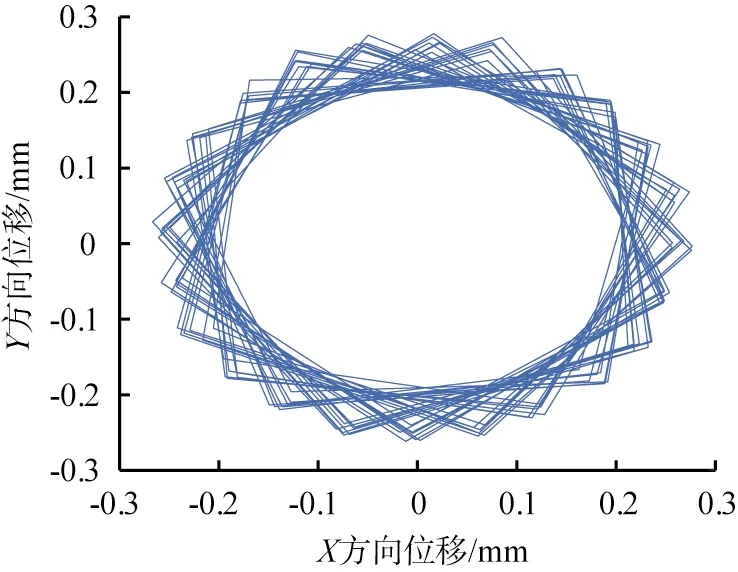
圖8 負載時內錐質心的平面運動軌跡

5 結論

1)通過建立振動慢剪破碎機內錐的動力學模型，使用MATLAB軟件，得到內錐的動力學響應，其主要運動為水平面內的振動圓運動。

2)使用ADAMS建立內錐的虛擬樣機模型，采用內錐標記MARKER點的方式描述內錐的運動軌跡，獲得空載下的內錐運動軌跡。使用ADAMS與EDEM耦合的方式，采用Tavares破碎模型，仿真振動慢剪破碎機鎢礦石顆粒破碎過程，分析內錐在負載下的運動軌跡，與所建立的空載下虛擬樣機模型內錐仿真運行軌跡、計算軌跡基本吻合。

3)通過數值計算、仿真、耦合仿真方法，驗證了振動慢剪破碎機結構設計的合理性，證明了破碎機部件的設計參數具有可行性，可為后續設計提供參照依據。