某城市軌道交通連續梁橋延性抗震設計

張素杰

(中國鐵路設計集團有限公司，天津 300308)

近年來，隨著我國城市軌道交通的不斷發展，結構類型也日趨多樣化，除地鐵外，高架橋梁結構也成為城市軌道交通的主要結構型式之一。由于軌道交通橋梁墩身截面尺寸相對較小，在地震作用下，更容易發生彎曲和剪切破壞，且震后破壞難以修復，因此抗震設計是軌道交通橋梁結構設計的重要控制因素。

在罕遇地震作用下，橋墩塑性鉸區的變形能力對延性抗震性能影響非常大，如何準確地模擬塑性鉸的受力狀態至關重要，Cofer等人在1998和2002年針對鋼筋混凝土橋墩采用有限元軟件分別建立了纖維模型、集中塑性鉸模型和三維實體模型進行模擬分析[1-2]，最終表明纖維模型的計算結果最接近實際情況。

目前對于市政工程、軌道交通、市域鐵路、城際鐵路等工程中橋梁結構的抗震設計，采用《公路橋梁抗震設計細則》《城市橋梁抗震設計規范》以及《鐵路工程抗震設計規范》居多，本文以天津市軌道交通Z4線一聯(30+50+30)m預應力混凝土連續梁為例，建立分布式纖維鉸有限元模型，對全橋進行罕遇地震下彈塑性時程分析，并按《城市軌道交通結構抗震設計規范》(GB50909-2014)(以下簡稱《城軌震規》)對橋墩進行延性抗震驗算，一方面為類似工程的延性抗震設計提供參考，另一方面對《城軌震規》在工程中的應用提供參考和補充。

1 工程概況

橋梁跨越現狀路開口采用(30+50+30)m預應力混凝土連續梁，P1(墩高12.5 m)、P4(墩高14.0 m)號墩分別為大小里程側邊墩，P2(墩高11.0 m)為固定墩，P3(墩高12.0 m)為活動墩。主梁為單箱單室箱梁，混凝土標號為C50。橋墩均采用Y型獨柱墩，墩身截面為矩形，混凝土標號為C50，邊墩采用8根?1.0 m鉆孔樁，主墩采用9根?1.2 m鉆孔樁，基礎混凝土標號為C45。

另外結合普通荷載工況及多遇地震分析計算，確定橋墩截面尺寸及配筋如表1所示。

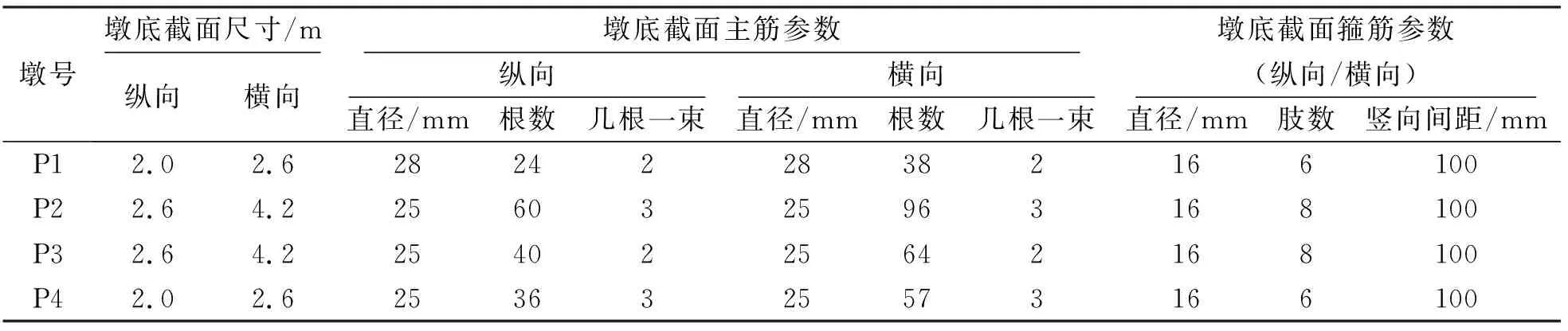
表1 各墩身截面及配筋參數表

2 建立有限元模型

采用Midas/Civil建立三維空間有限元模型，采用空間梁單元模擬主梁、橋墩以及承臺；大小里程側簡支梁跨利用集中質量節點模擬，施加于兩側邊墩，結合簡支梁實際支座布置，順橋向節點質量為一孔簡支梁及橋面質量，橫橋向節點質量為一孔簡支梁及橋面質量的一半。采用彈性連接模擬固定及縱向活動支座，在承臺底采用節點彈性支承模擬樁土相互作用，計算模型如圖1所示。

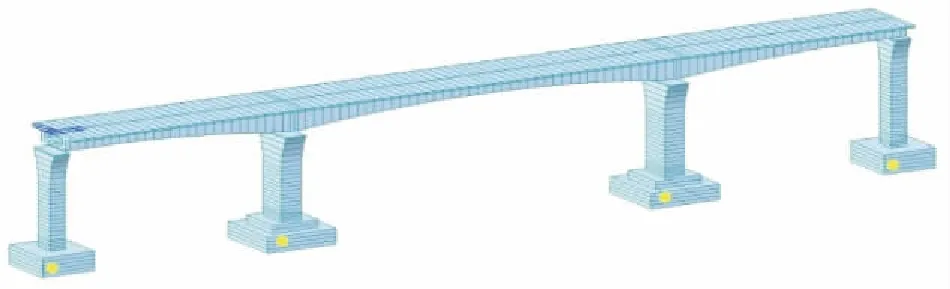
圖1 有限元計算模型

2.1 等效塑性鉸長度計算

在進行罕遇地震下橋梁延性計算時，需要在墩底設置塑性鉸，而如何確定等效塑性鉸長度Lp至關重要，它對橋墩的塑性變形發展以及墩頂極限位移影響非常大[3]。目前對于其計算公式，國際上并沒有統一的標準，我國《公路橋梁抗震設計細則》(JTG/TB02-01-2008)在Paulay與Priestly(1992) 提出的經驗塑性鉸區高度公式[4]基礎上做了輕微修正，取下面兩式較小值：

Lp=0.08H+ 0.022fyds≥0.044fyds

(1)

Lp=2b/3

(2)

式中：H為懸臂墩高度或塑性鉸截面到反彎點距離(mm)；b為矩形截面短邊尺寸或圓形截面直徑(mm)；fy為縱向鋼筋抗拉強度標準值(MPa)；ds為縱向鋼筋直徑(mm)。

本設計據此計算P1～P4號墩塑性鉸長度分別為1.31 m、1.16 m、1.24 m、1.33 m，在模型中各墩底相應高度范圍賦予其非彈性鉸特性。

2.2 材料的本構關系

采用分布式纖維模型模擬塑性鉸，各墩底截面被分為若干纖維[5-7]，其中鋼筋的應力-應變本構關系采用雙折線模型，其應力應變關系曲線如圖2所示；保護層混凝土、約束混凝土采用由Mander等[8]人提出的混凝土應力-應變關系模型，其應力-應變關系曲線如圖3所示。

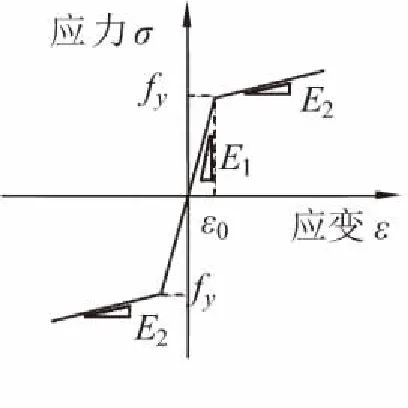
圖2 鋼筋應力-應變關系

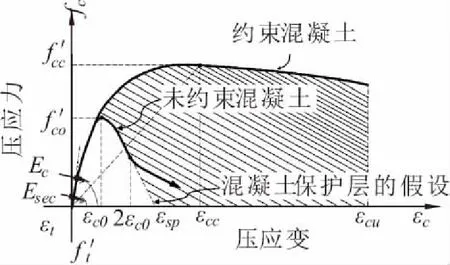
圖3 混凝土應力-應變關系

約束混凝土應力-應變關系可由下列公式確定：

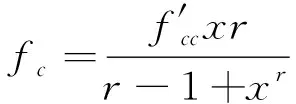
(3)

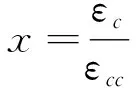
(4)

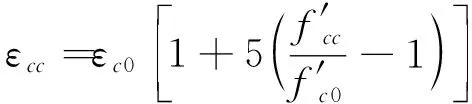
(5)

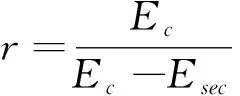
(6)

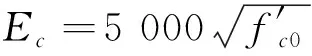
(7)

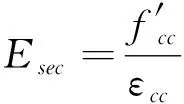
(8)

式中：fc為混凝土壓應力；εc為混凝土壓應變；f′cc為約束混凝土抗壓強度；εcc為約束混凝土抗壓強度對應的應變；f′co為混凝土抗壓強度標準值；εc0為抗壓強度標準值對應的應變。

3 動力彈塑性分析

3.1 地震時程

采用該項目地震安評報告中3條50 a超越概率2%地震波輸入模型進行計算，3條地震波時程曲線如圖4所示。

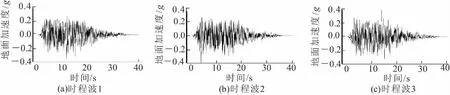
圖4 地震動加速度時程波

3.2 彈塑性分析結果

模型按照3條罕遇地震波分縱橫向輸入，根據墩底塑性鉸單元彎矩時程結果與對應截面“彎矩-曲率”曲線中屈服彎矩比較判斷其是否屈服，具體判斷結果如表2所示。

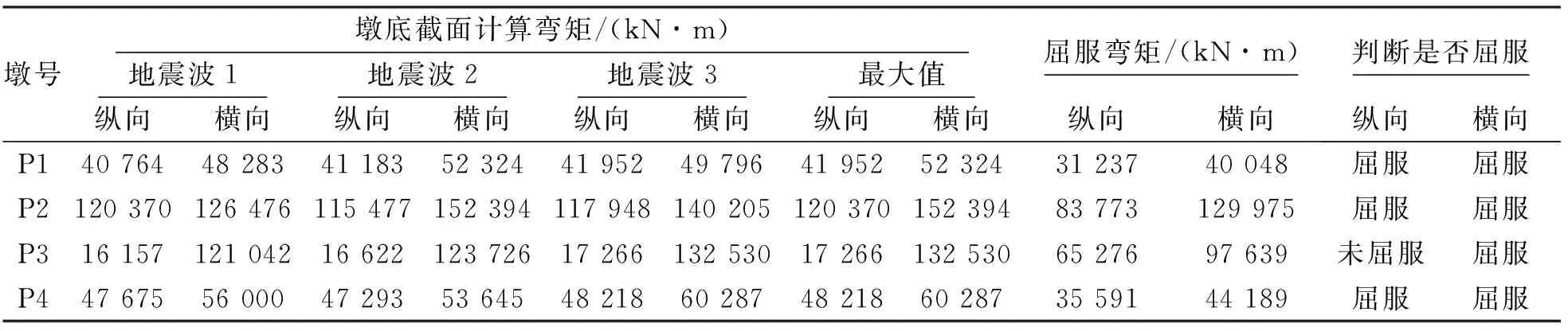
表2 各墩底塑性鉸截面屈服判斷

由表2結果可知，在3條地震波作用下，除P3號活動墩在地震波縱向作用下以及P2號固定墩在地震波1橫向作用下未達到屈服之外，其余橋墩墩底塑性鉸均達到屈服，需要根據規范進行延性指標驗算；同時對P2、P3號墩在相應地震波作用下進行彈性分析，結果滿足要求，此處不再贅述。

3.3 延性指標驗算

根據《城軌震規》3.1.2以及相應條文說明判定該連續梁屬于重點設防類橋梁結構，橋墩延性驗算指標分為強度驗算和變形驗算，在強度驗算過程中需判斷構件破壞形式，在變形驗算過程中確定構件性能等級，并判斷其變形是否符合規范中該類構件(重點設防類)的性能等級要求。

3.3.1 強度驗算及破壞形式判斷

根據《城軌震規》7.2.1條規定，鋼筋和鋼骨混凝土柱式構件的破壞形態以及抗剪驗算按下列公式進行判定。

彎曲破壞形式Vmu≤Vyd

(9)

剪切破壞形式Vmu>Vyd

(10)

抗剪驗算 0.85Vyd≥Vo

(11)

Vyd=Vcd+Vwd+Vsd

(12)

式中：Vmu為構件達到截面等效屈服彎矩時的剪力(kN)；Vyd為設計剪切抗力(kN)；Vo為剪力需求(kN)；Vcd為混凝土的設計剪切抗力(kN)；Vwd為鋼筋的設計剪切抗力(kN)；Vsd為鋼骨的設計剪切抗力(kN)。

根據模型計算墩底塑性鉸單元剪力時程結果(剪力需求)與根據截面尺寸及主筋和箍筋配置，按照《城軌震規》附錄F.1中鋼筋混凝土構件抗剪能力計算方法計算，所得各項參數結果詳見表3所示。

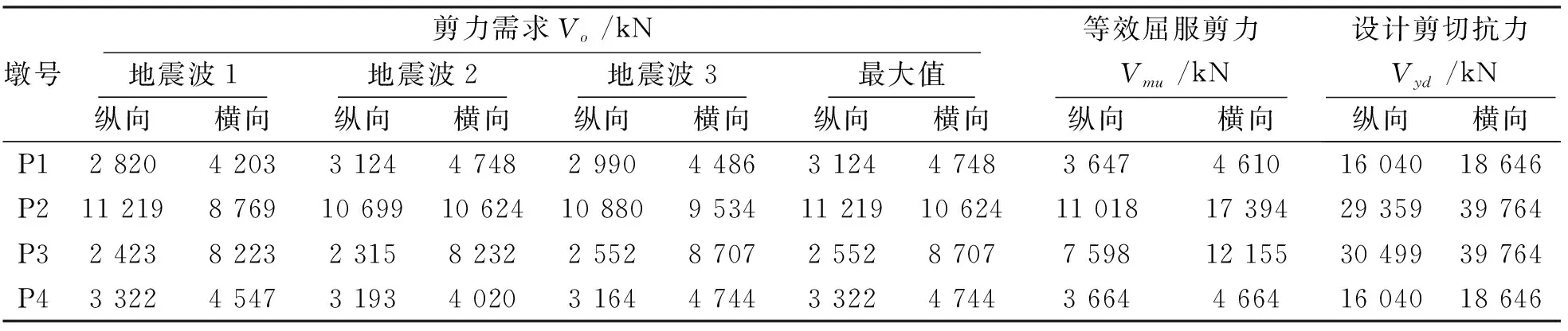
表3 強度驗算及破壞形式判斷過程

由表3結果可知，在3條地震波作用下，各墩底截面縱橫向等效屈服剪力均小于設計剪切抗力，判斷截面破壞形式均為彎曲破壞；同時各墩底截面縱橫向剪力需求均小于0.85倍設計剪切抗力，滿足規范中強度驗算要求。

3.3.2 變形驗算及構件性能等級判斷

根據模型在各地震波作用下墩底截面內力計算結果，計算得各墩軸壓比最大值為0.05，縱橫向剪跨比最小值為2.8。根據《城軌震規》7.2.2條規定，對于軸壓比小于0.5且剪跨比為1.5以上鋼筋混凝土構件，其彎曲變形性能按照等效理想彈塑性彎矩-轉角關系確定(如圖5所示)。

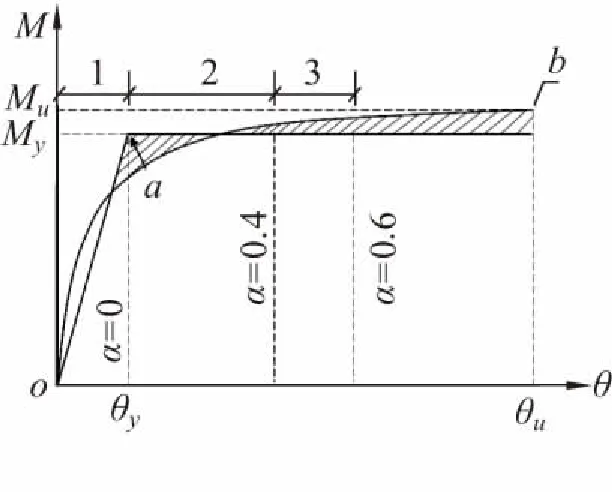
圖5 構件的彎矩和轉角的關系

對于判別為彎曲破壞的小軸壓比構件，其性能等級可按構件轉角或塑性鉸區轉角劃分，按照《城軌震規》，其界限值可按下列公式確定。

(13)

θpu=(?u-?y)Lp

(14)

式中：θd為性能等級的界限值(rad)；θy為截面等效屈服點對應塑性鉸區轉角；K為構件極限塑性轉角的安全系數；α為構件性能等級系數；θpu為構件塑性鉸區的極限塑性轉角(rad)；?u為塑性鉸區極限曲率；?y為塑性鉸區屈服曲率；Lp為塑性鉸區長度(m)。

根據模型計算墩底塑性鉸單元轉角時程結果(構件需求轉角)與截面尺寸及主筋和箍筋配置，按照《城軌震規》附錄G.1中鋼筋混凝土構件變形能力計算方法計算，所得截面等效屈服點和極限變形點對應對應塑性鉸區轉角以及構件塑性鉸區極限塑性轉角詳見表4。

由表4可以判斷各橋墩結構性能等級并確定相應其性能等級的轉角界限值，如表5所示。

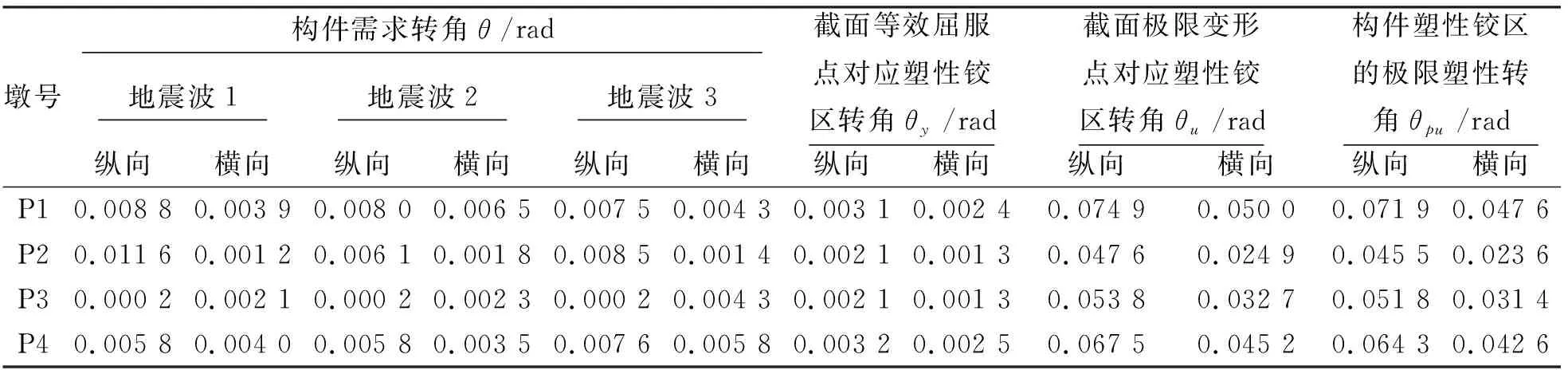
表4 變形驗算及構件性能等級判斷過程

表5 變形驗算及構件性能等級判斷結果

結合表4～表5結果可以判斷各橋墩在3條地震波作用下的需求轉角均小于構件性能等級界限值，滿足《城規震規》變形驗算要求。該連續梁屬于重點設防類結構，根據《城規震規》要求，需要滿足罕遇地震下性能要求Ⅲ：構件、基礎的性能等級要求不應低于3，結合表5結果可以判斷該連續梁結構滿足規范抗震性能要求。

4 結論

(1)除P3號活動墩在地震波縱向作用以及P2號固定墩在地震波1橫向作用下未達到屈服之外，其余橋墩墩底塑性鉸截面均達到屈服，進入塑性狀態。

(2)各墩底截面縱橫向等效屈服剪力均小于設計剪切抗力，判斷截面破壞形式均為彎曲破壞，同時各墩底截面縱橫向剪力需求均小于0.85倍設計剪切抗力，滿足規范中強度驗算要求。

(3)各橋墩需求轉角均小于構件性能等級界限值，滿足規范中變形驗算要求，該連續梁結構滿足重點設防類結構抗震性能要求。