多裂紋對裂紋搭接規律影響數值模擬及機理研究

趙 楠，李萬渠，馮金鈺，王奕儒, 李 麗

1四川水利職業技術學院 2中國石油長慶油田蘇里格南作業分公司作業一區 3中國石油青海油田分公司勘探開發研究院

0 引言

裂隙廣泛存在于巖體結構中[1-2]，在復雜應力條件下裂縫的擴展貫通是導致工程結構失穩的關鍵因素[3-4]。裂隙的存在降低了材料的剛度與強度，裂紋尖端的應力集中使得工程結構更加容易失效，因此對含裂隙材料及結構的裂隙擴展規律及機理的研究則顯得尤為重要。

對于含裂隙材料的失效過程研究較多，在室內試驗研究方面：董振興[5]對水壓及雙軸作用下的含穿透型裂隙的裂紋擴展進行了室內試驗研究，得到了試樣的起裂應力、峰值強度及裂紋的發展過程；梅比[6]基于動態焦散線實驗系統，對含缺陷的PMMA板進行了三點彎沖擊試驗；王蒙[7]采用則分離式霍普金森壓桿(SHPB)，對SCSCC試樣I—II復合型裂紋進行動態斷裂試驗。

在理論判據方面：李勇明等[8]建立了綜合考慮儲層所處地應力、多裂紋相互作用的裂紋擴展模型；劉雨等[9]對儲層的水力裂縫與天然裂縫的交匯判別準則進行了推導驗證。

在數值模擬方面：王杰[10]基于單元破裂法對巖石的裂紋擴展過程進行了描述；蔣明鏡[11]基于離散單元法，對含雙裂隙標準立方體模型進行了單軸壓縮數值模擬試驗；王洪建[12]利用擴展有限元法對巖石的斷裂過程進行了分析。但是，以往的研究多針對一條或兩條類型進行研究，裂隙往往成陣列形式存在于結構中。將實際問題抽象成單條或兩條裂隙很難描述裂隙之間的相互作用規律。

1 數值計算理論

1.1 本構關系

巖石的應力—應變關系主要由平衡方程、應力—應變方程及應力—應變關系三個方程來進行描述。

(1)平衡微分方程：

σij,j+Fi=0(i,j=1,2,3)

(1)

式中：σij—計算過程中的總應力,Pa；

Fi—體積力,m3。

(2)應力—應變方程：

(2)

式中：εij—應變張量；

μi—位移張量；

μi，j—位移梯度張量。

(3)應力—應變關系:

(3)

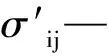
λ、G—Lame常數；

εv—體積應變；

δij—克羅內克函數。

1.2 損傷過程描述

在數值計算過程中，每一個單元的應力分量滿足破壞準則時，單元將發生破壞。因此，根據以往損傷處理經驗，其損傷后的彈性模量可表達為：

E=(1-D)E0

(4)

式中：D—損傷程度表征；E和E0—已經損傷以及還沒有損傷的單元的彈性模量。

同時，當拉應力分量超過材料抗拉強度時，損傷程度表征可以寫成：

(5)

式中：ftr—殘余抗拉強度,MPa；εt0和εtu—分別表示彈性極限拉伸應變和單元極限拉伸應變。

根據以往數值處理經驗，選取Mohr-Columb作為損傷破壞準則，可以同時表征單元的拉伸破壞與剪切破壞，可以表達成為：

(6)

式中：φ—單元的內摩擦角,(°)；fc—單元的抗壓強度,MPa。

因此，單元在壓縮條件下的損傷程度表征可以表示為

(7)

2 計算模型和參數

建立二維有限元模型，其模型尺寸為150 mm×200 mm，單條裂隙的長度為20 mm，裂隙寬度為1 mm。

模型分為兩組，一組為含不同裂隙條數(編號為A)，裂隙角度確定為45°，裂隙條數分別為A1：15條，A2：20條，A3：25條及A4：30條；另一組為含不同傾角裂隙(編號為B)，裂隙條數為15條，裂隙角度分別為B1：25°，B2：45°，B3：75°及B4：90°。模型受到單軸應力作用，采用位移加載模式，加載速率為0.004 mm/計算步。不同工況的數值計算模型如圖1所示，模型參數如表1所示。

圖1 不同工況數值計算模型

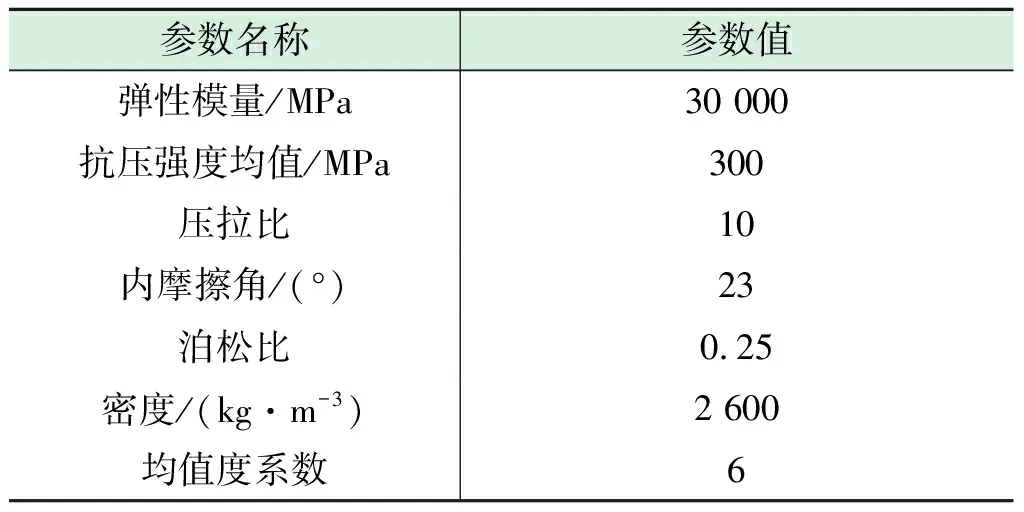
表1 材料基礎參數

3 結果分析

3.1 裂紋漸進破壞過程

不同裂隙密度及傾角下的裂紋漸進破壞過程如圖2所示。

由圖2可見，對于模型A裂隙傾角為45°不同裂隙密度而言，翼型裂紋首先在預制裂紋尖端產生，隨后翼型裂紋發展成為拉伸裂紋，逐漸沿著最大主應力方向發展，值得注意的一點是，靠近模型邊界的預制裂紋，其翼型裂紋發展程度要大于位于模型內部的預制裂紋，這應是由于邊界效應所導致。另外，翼型裂紋擴展后期，反翼型裂紋將從翼型裂紋相反方向產生，翼型裂紋尖端會相互搭接。同時剪切裂紋將從預制裂紋的中部產生，與翼型裂紋、反翼型裂紋相互作用，形成復雜的裂隙網絡。預制裂隙的密度越大，模型的邊界效應將會減小，同時裂隙網絡的發展將會越復雜。

而模型B僅含15條預制裂紋，但就裂隙角度不同的情況而言，模型B預制裂隙的傾角較小時(傾角為25°)，翼型裂紋沿著預制裂紋的內部產生，其擴展方向為最大主應力方向，存在邊界效應，與模型A類似。但是對于裂隙傾角較大的情況(傾角為75°)，預制裂隙尖端產生翼型裂紋擴展，但擴展程度較小，隨后剪切裂紋主導了模型的破壞，對于裂隙傾角為90°的情況，翼型裂紋同樣也并非從裂紋尖端產生，最終模型的破壞模式為以剪切破壞。

3.2 應力—應變曲線

不同裂紋密度及裂紋傾角下的試樣應力—應變曲線如圖3所示。

由圖3可見,單軸壓縮下，試樣的應力—應變規律主要表現為三個典型特征：①線彈性階段,此時應力—應變曲線呈現直線規律；②非線性階段,由于這個階段裂隙萌生并擴展，其應力—應變曲線偏離直線變形，從而導致模型剛度非線性降低；③殘余變形階段,這個階段應力跌落，應變增大，模型破壞。

圖3 不同裂紋密度及裂紋傾角下的試樣應力—應變曲線

對于模型A含不同裂紋密度情況而言，裂紋的密度越大，模型的峰值應力越小。對于模型A1而言，不同裂紋密度模型的峰值強度分別降低百分比為4.3%，4.7%及18.8%，可見裂紋密度對模型峰值強度影響較大，同時當裂紋密度增大到一定程度時模型峰值強度會有一個突然的跌落。對于模型B含不同裂紋角度情況而言，裂隙角度的增大則對模型的峰值強度有一個提高的作用，相對于模型B1而言，不同裂隙角度的增大對模型峰值強度提供的百分比分別為13.2%，45.2%及61.9%，因此就本文

數值模擬結果而言，裂隙角度對模型峰值強度的影響要大于裂紋密度。

4 結果對比

本文的數值模擬結果和以往室內試驗結果[13]的對比結果如圖4所示。

圖4 數值模擬與室內試驗對比

由圖4可見，數值模擬結果與室內試驗呈現高度一致性。在模型B1中，靠近邊界的預制裂隙翼型裂紋擴展程度要大于內側裂隙，即出現明顯的“邊界效應”，同時，翼型裂紋并不都是從預制裂紋的尖端產生；在模型A4中，多裂紋間的翼型裂紋、反翼型裂紋及剪切裂紋相互搭接，其裂紋擴展模式也與室內試驗一致，因此，本文的數值模擬可以準確的反映實際材料的破裂過程及其特征。

5 結論

(1)本文建立了含不同密度及傾角裂隙的有限元計算模型，翼型裂紋、反翼型裂紋在預制裂紋尖端及靠近尖端產生，剪切裂紋產生與裂紋中部，靠近模型邊界的預制裂紋存在“邊界效應”。

(2)不同裂紋密度模型的峰值強度分別降低百分比為4.3%，4.7%及18.8%，不同裂隙角度的增大對模型峰值強度提供的百分比分別為13.2%，45.2%及61.9%，裂隙角度對模型峰值強度的影響要大于裂紋密度。

(3)數值模擬結果與試驗結果對比，驗證了本文數值模擬的正確性。