氣侵初期環空壓力瞬態變化規律研究

劉鳳和，程長坤，譙世均，邢 星，吳玉杰，楊宏偉

1中國石油青海油田分公司 2中國石油青海油田分公司鉆采工藝研究院 3中國石油青海油田分公司工程技術處 4中國石油大學(北京)石油工程學院

0 引言

水錘效應是由于流體動量的突然變化而引起的一系列壓力交替變化的現象，在油氣鉆采過程中很常見。但氣侵初期的水錘現象在早期氣侵的發現中仍然是一個被忽略的問題。

氣侵時環空壓力的變化通常采用氣液兩相流模型來模擬，氣液兩相流模型包括均相流模型、雙流體模型和漂移流模型[1-3]。相對于均相流模型和雙流體模型，漂移流模型考慮了氣液兩相之間的滑脫效應以及空隙率、流速沿過流斷面的分布規律，使兩相流動計算誤差顯著地降低[4-6]，該模型由Zuber和Findlay提出并得到廣泛應用[7]。隨后很多學者對漂移流模型進行了擴展，并應用其模擬氣侵時井筒氣液兩相瞬態流動問題[8-10]，但是漂移流模型無法捕獲氣侵初期地層氣體迅速進入井筒時引起液柱壓力的瞬態變化特征。氣侵初期，地層氣體快速進入井筒使氣液交界面之上的鉆井液速度突然增加，產生水錘效應。為了準確模擬氣侵初期環空壓力的瞬態變化規律，考慮了氣侵初期的水錘效應，建立了一個水錘—漂移流綜合模型來描述氣侵過程中環空壓力的瞬態變化規律，并采用基于一階精度的Lax-Friedrichs格式和二階精度的MacCormack格式的復合差分格式對該模型進行了求解。模型和數值算法的可靠性和準確性通過Wang[11]氣侵實驗的測量壓力數據進行了驗證。

利用此模型可以準確地捕獲氣侵初期井底壓力的瞬態變化規律，以期為早期氣侵檢測提供了理論依據,對發現早期氣侵有積極作用,有利于保障井控安全。

1 物理模型

氣侵過程中，地層和井筒的整個系統內流體流動狀態可以分為三個獨立的區域：①地層氣體向井筒滲流區域，如圖1中的區域1；②氣體在環空中向上運移，形成一個氣液兩相流動區域，如圖1中的區域2；③僅包括鉆井液的單相流動區域，如圖1中的區域3。兩相流區域和單相流區域由氣液交界面分隔。

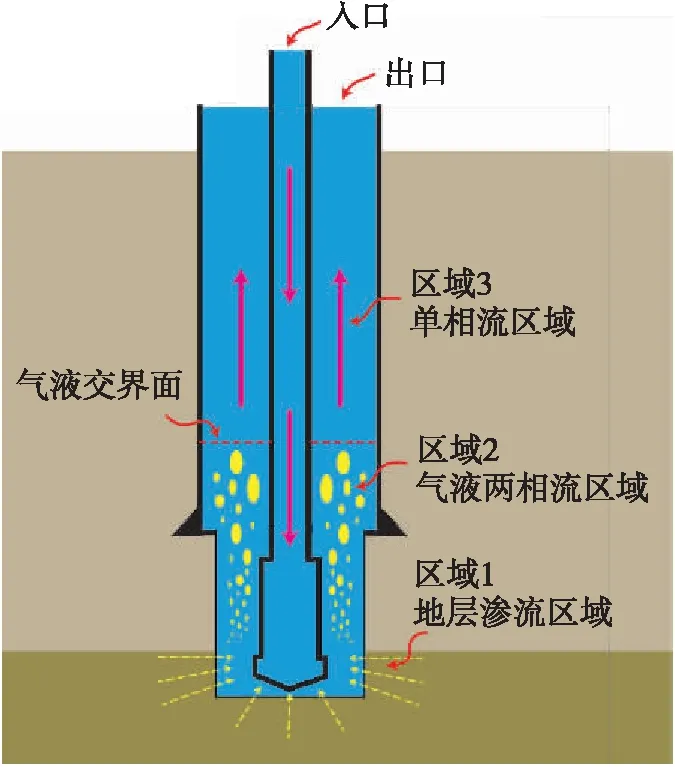
圖1 氣侵時不同區域內流體的瞬態流動圖

為建立數學模型準確描述氣侵過程中各區域內流體的瞬態流動規律，做出如下的假設：①只考慮沿井筒軸向的一維問題，忽略徑向和切向的變化；②直井鉆井過程中，氣侵發生在井筒底部；③不考慮氣體在鉆井液中的溶解；④不考慮系統的能量守恒關系，假設井筒中存在一個已知的溫度梯度。

2 數學模型

2.1 水錘模型

氣侵發生后，氣體迅速由地層進入井筒，導致區域3中的泥漿柱速度突然增加，引起水錘效應。區域3中的流體僅由鉆井液組成，采用單相流水錘模型來描述氣侵初期泥漿柱的水錘效應。

一維經典的水錘模型控制著瞬態管流的場變量隨空間和時間的變化，可以由質量守恒方程和動量守恒方程推到得出，氣侵時水錘模型的控制方程如下[12-13]：

(1)

(2)

式中：vl—液體流速，m/s；ρl—液體密度，kg/m3；p—環空壓力，Pa；f—摩阻系數；d0—井眼直徑，m；dp0—鉆柱外徑，m；θ—井斜角，(°)；g—重力加速度，m2/s；a—壓力波傳播速度，m/s。

2.2 漂移流模型

氣侵發生后，氣體由地層進入井筒，并在環空內向上運移，形成一個氣液兩相流區域。氣液兩相流動過程中主要會發生三種物理現象：相間的質量交換、流體的質量傳遞和壓力波的傳播。氣液兩相流可以采用漂移流模型模擬井筒壓力的瞬態變化，其包含了各相的質量守恒關系和混合動量守恒關系。守恒方程的閉合系統是由各相速度間的滑移關系組成。

氣相質量守恒方程:

(3)

液相質量守恒方程:

(4)

混合動量守恒方程:

=-ρmgcosθ-Ff

(5)

式中：ρm=αgρg+αlρl；αg—氣體的體積分數；αl—液體的體積分數；ρg—氣體密度，kg/m3；vg—氣體速度，m/s；Гg→l—氣相和液相之間的質量交換速率，kg/(m3·s)；qsg—氣體質量流量，kg/(m3·s)；Ff—環空摩阻項，Pa/m。

漂移模型能夠準確地描述氣相和液相之間的相互作用機理[14]，并采用速度分布系數來描述各相流動與整體流動之間的關系。氣侵發生時，氣體在環空中運移的真實速度表示為：

vg=c0vm+v0

(6)

式中：vm=αgvg+αlvl；c0—分布系數，它描述了氣液兩相流中速度和體積分數剖面的分布特性；v0—由浮力作用引起的氣相滑脫速度，m/s。c0和v0由流型決定，這里采用由Perez提出的模型進行計算。

2.3 地層滲流模型

鉆至儲層時，如果井底壓力低于地層壓力，地層中的氣體便會侵入井筒。氣體由地層侵入井筒符合非達西滲流，可以使用二項式定理計算產氣速率[15]。

(7)

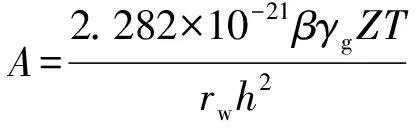
(8)

(9)

式中：pe—地層壓力，MPa；pwf—井底壓力，MPa；qg—氣侵速率，m3/d；β—紊流系數；γg—氣體比重；rw—裸眼半徑，m；re—供給半徑，m；h—儲層厚度，m；μg—氣體黏度，mPa·s；k—地層滲透率，μm2；S—表皮系數。

3 數值解法

3.1 數值格式

水錘模型和漂移流模型的控制方程均表現出一階線性雙曲型方程組的特點[16-17]，描述了密度波沿流體流動的下游方向傳播和壓力波沿流體流動的下游和上游方向傳播的物理現象。因此水錘模型和漂移流模型的控制方程可以寫成如下緊湊形式:

(10)

式中：w=(αgρg,αlρl,αgρgvg+αlρlvl)T—守恒型參數，是獨立物理變量u=(αg,p,vg,vl)T的函數。在水錘模型中，αg=0，vg=0。

利用基于一階精度的Lax-Friedrichs格式和二階精度的MacCormack格式的復合差分格式對方程(10)進行求解，該方法是以MacCormack格式為基礎，每隔5 000個時間步采用具有數值耗散作用的Lax-Friedrichs格式進行一個時間步長的計算。將長為L的井筒沿軸線方向劃分為N個網格，其中zi=z0+iΔz，i=1,2,…,N，Δz=L/N，如圖2所示。根據數值求解穩定性的要求，空間步長與時間步長的選取要滿足CFL(Courant-Friedrichs-Lewy)條件。

一階精度的Lax-Friedrichs格式具有如下的守恒形式:

(11)

其中數值通量表示為:

(12)

MacCormack方法是一個三點預測校正的中心差分格式，它的預測步采用向前差分，校正步采用向后差分。預測步的差分格式可表示為:

(13)

校正步的差分格式可表示為：

(14)

其中數值通量可表示為：

(15)

3.2 邊界條件處理

氣侵發生時，在井底控制體入口處將氣侵速率視為已知條件，在井口控制體出口處，將出口壓力視為已知條件。由于式(11)～式(15)為三點中心差分格式，無法處理邊界條件，因此邊界條件需要進行特殊處理。Pauchon和Dhulesia提出可以利用相容性方程對邊界條件進行處理[18]。

3.3 求解過程

基于上述數學模型、數值算法以及邊界條件，便可以模擬氣侵過程中井筒壓力的瞬態變化規律，主要的計算流程如圖3所示。

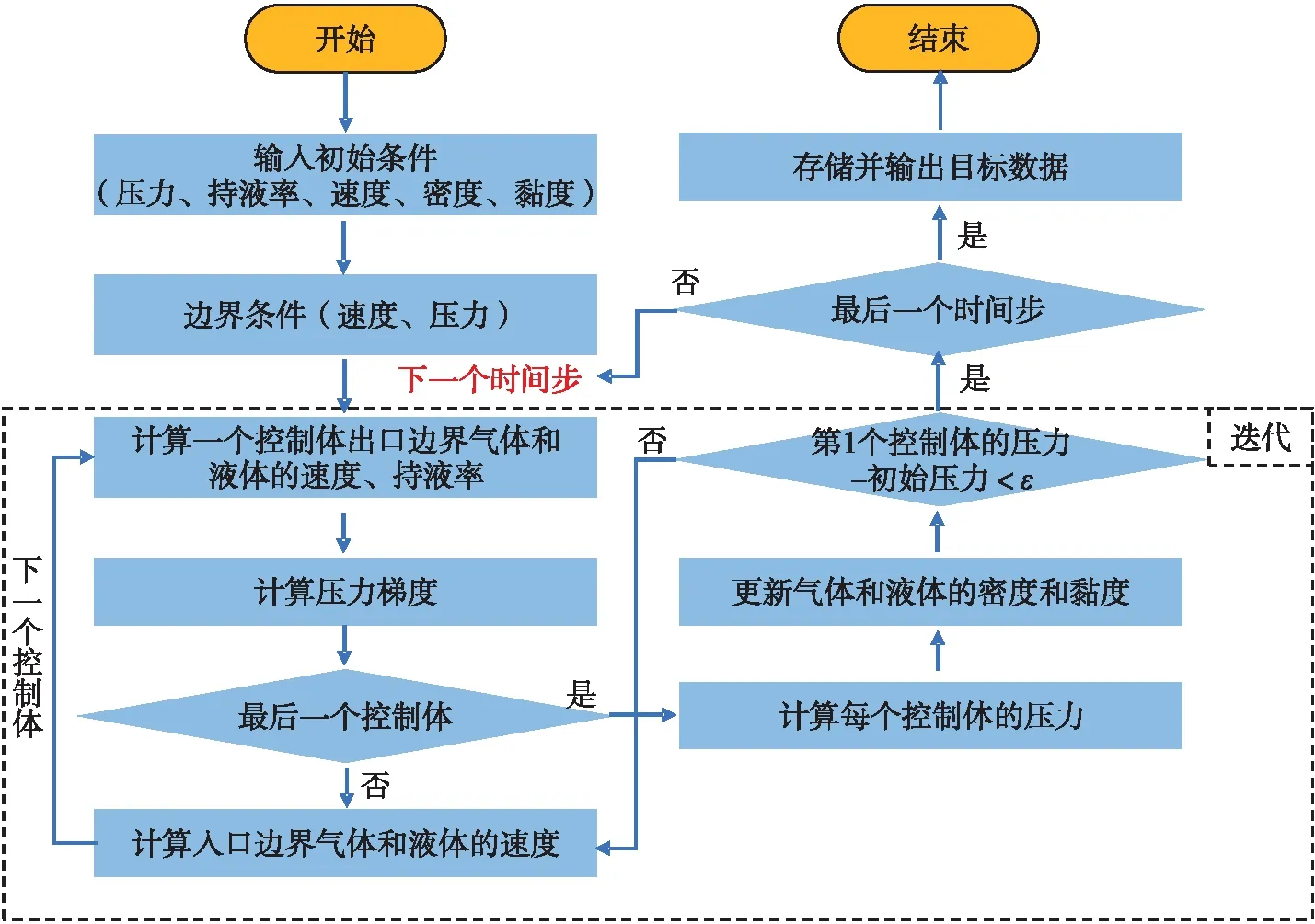
圖3 主要計算流程圖

4 模型驗證

利用Wang[11]在全尺寸氣侵實驗中獲得的瞬態壓力數據對水錘—漂移流綜合模型和數值算法的可靠性和準確性進行驗證。該實驗包括兩口井，其中一口井為實驗井，另一口井為儲氣井。儲氣井通過一根直徑為60.3 mm的管柱向實驗井中注氣，注氣位置為井深600 m處。實驗井井眼尺寸為?244.5 mm，鉆柱外徑為127 mm，鉆頭和PWD工具的井深分別為600 m和580 m,鉆井液排量為24 L/s,實驗中用水和空氣分別代表鉆井液和地層氣體。

圖4為測量壓力和模擬壓力的分布規律。在實驗開始的第75 s開始注氣,第200 s停氣，注氣速度為27 L/s，由圖4可知，模擬壓力與測量壓力的吻合度較好，模擬壓力很好的描述了氣侵實驗中井筒壓力的瞬態變化規律。如圖5所示，模擬壓力相對于實驗測量壓力的誤差均在±10%以內。所以，基于水錘—漂移流綜合模型可以準確地預測井筒壓力的瞬態變化規律。

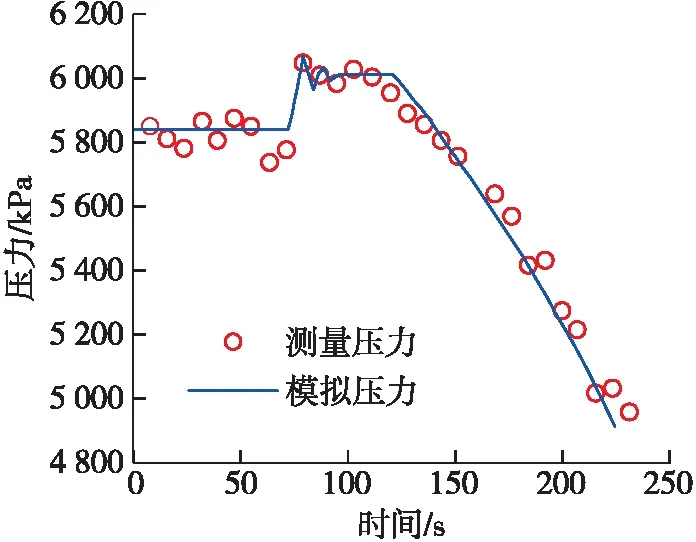
圖4 測量壓力和模擬壓力隨時間的變化規律

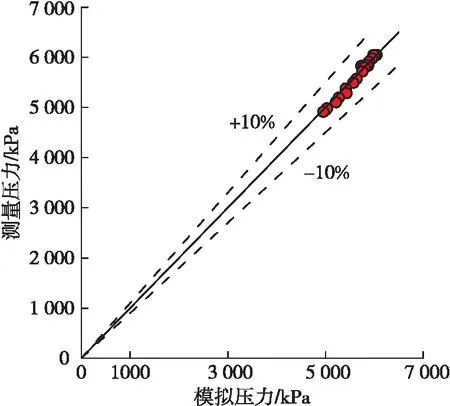
圖5 模擬壓力相對于測量壓力的誤差

5 實例分析

利用水錘—漂移流綜合模型驗證一口柴達木盆地尖北地區實鉆井氣侵初期的環空壓力變化和環空壓力對各個影響因素的敏感性。基礎參數如下：直井井深4 200 m，水基鉆井液的密度為1 200 kg/m3，塑性黏度為15 mPa·s，動切力為9 Pa，水錘模型計算中采用修正冪律模式，氣體比重為0.7，鉆井液排量為30 L/s，地層壓力為54 MPa，滲透率為0.175 μm2，地層供給半徑為150 m。

井身結構為：?339.7 mm表層套管×1 200 m+?244.5 mm技術套管×4 200 m;鉆具組合為:?215.9 mm PDC鉆頭+?157.5 mm螺桿鉆具×9.2 m+?157.5 mm鉆鋌×63 m+?127 mm加重鉆桿×27 m +?127 mm鉆桿。

5.1 氣侵初期環空壓力變化分析

圖6為井底發生氣侵時，氣侵速率隨時間的瞬態變化規律。由圖6可知，氣侵發生后，地層氣體開始會以較大的加速度迅速進入井筒，在ts時刻氣侵速度達到擬穩定狀態，之后氣侵速度隨著井底壓力的降低逐漸升高。將開始發生氣侵到ts時刻的時間間隔定義為瞬態氣侵時間，將ts時刻的氣侵速率定義為瞬態氣侵速率。

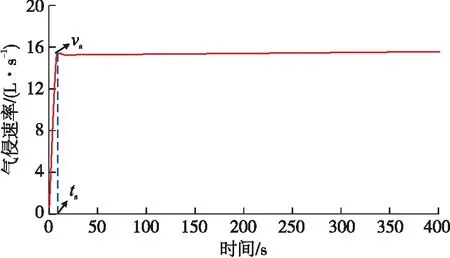
圖6 氣侵速率隨時間的瞬態變化曲線

圖7為氣侵初期井深4 170 m處環空壓力隨時間的瞬態變化規律。由圖7可知，氣侵發生后，地層氣體迅速進入井筒導致泥漿柱速度突然增加，引起水錘現象，水錘壓力迅速增加并隨時間呈周期性波動；水錘壓力的振幅隨時間逐漸減小，且第一個(即最大的)波峰發生在瞬態氣侵時間ts之后；一段時間后，環空壓力開始隨時間近似線性降低，這是因為氣液交界面上升至4 170 m處，該處的部分鉆井液被氣體代替形成氣液兩相流區域，從而導致該處環空壓力降低。

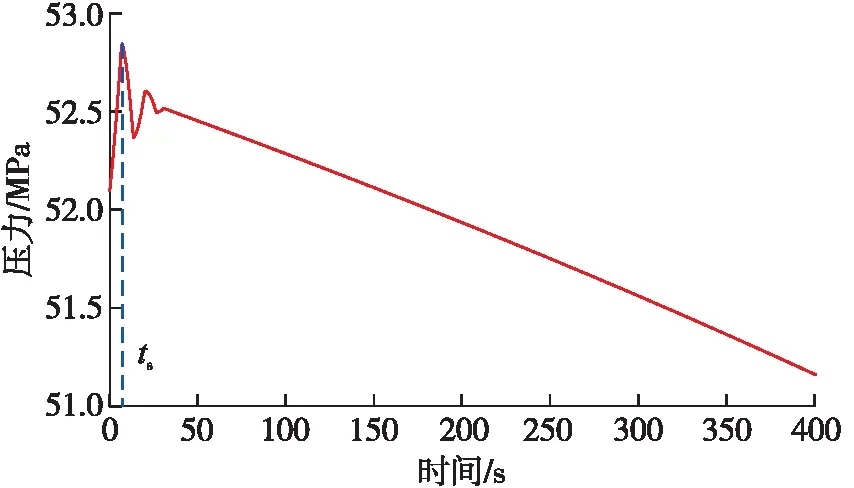
圖7 井深4 170 m處環空壓力隨時間的瞬態變化曲線

圖8為不同井深處氣侵初期的環空壓力與正常鉆進時相應位置處環空壓力的比值，將此比值定義為相對環空壓力比。氣侵初期氣液交界面以上不同井深處相對環空壓力比近似相等；隨著井深的減小，氣液交界面上升至相應位置的時間增加，因此環空壓力開始降低的時間也增加，這可以作為氣液交界面位置追蹤的依據，且不同時間段內不同井深處相對環空壓力比之間的一致性和差異性為多測點早期氣侵識別提供了理論依據。

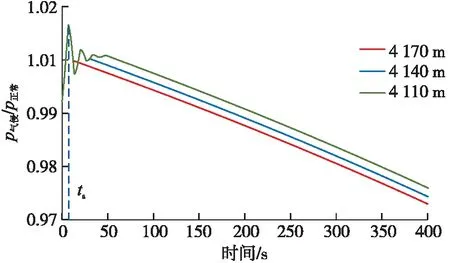
圖8 不同井深處氣侵初期與正常鉆進時相應位置處的環空壓力比

5.2 氣侵初期井底壓力敏感性分析

圖9為當瞬態氣侵時間為7 s時，井深4 170 m處不同瞬態氣侵速率條件下的環空壓力瞬態變化曲線。由圖9可知，氣液交界面上升至4 170 m之前，瞬態氣侵速率越大，水錘效應越明顯，水錘壓力波動振幅越大，水錘壓力增量越大，氣液交界面上升至該位置的時間越短，但瞬態氣侵速率對水錘壓力的波動頻率幾乎沒有影響。當氣液交界面上升超過4 170 m后，該處環空壓力受漂移流模型控制，隨著瞬態氣侵速率的增加，環空壓力的下降速度增大。

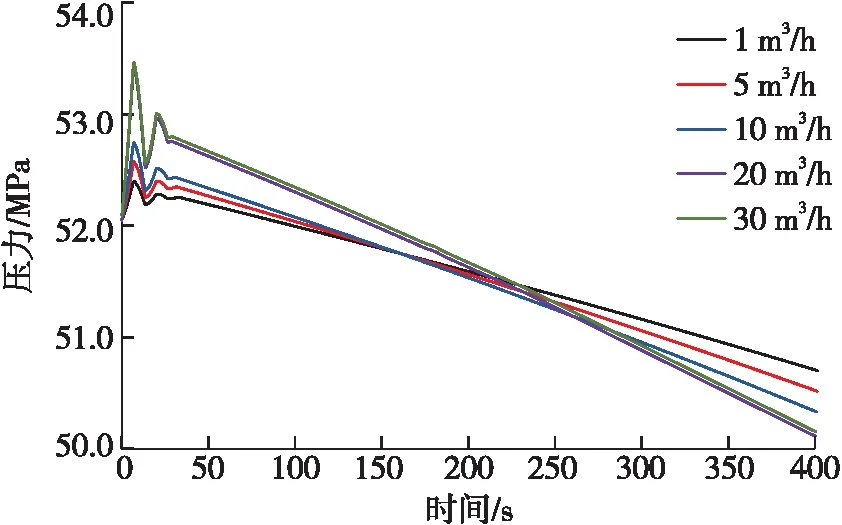
圖9 不同瞬態氣侵速率條件下的環空壓力瞬態變化曲線

圖10為當瞬態氣侵速率為15 L/s時，井深4 170 m處不同瞬態氣侵時間條件下的環空壓力瞬態變化曲線。由圖10可知，氣液交界面上升至4 170 m之前，隨著瞬態氣侵時間的減小，水錘效應更加明顯，水錘壓力波動振幅和波動頻率均增大，但氣液交界面上升至該位置的時間幾乎相同；當氣液交界面上升超過4 170 m后，不同瞬態氣侵時間條件下的環空壓力均相等，且下降速率也相同。所以瞬態氣侵時間僅對氣侵初期的水錘效應有較大的影響，但對于兩相流區域內的環空壓力變化幾乎沒有影響。

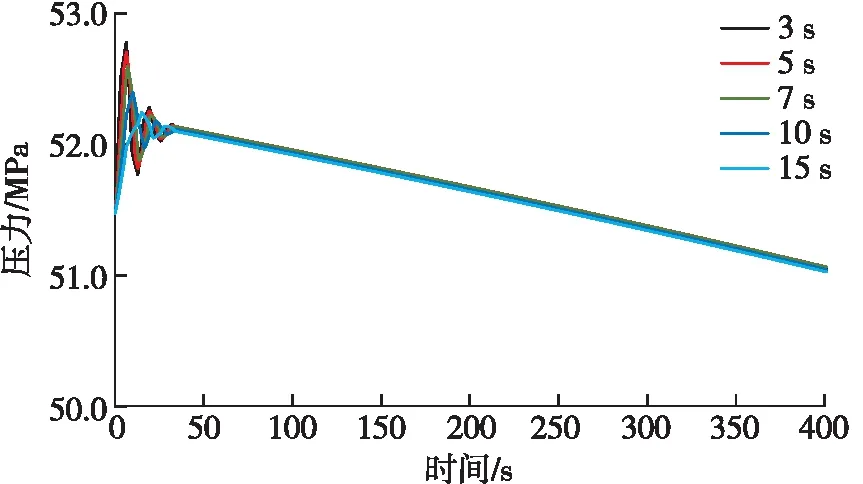
圖10 不同瞬態氣侵時間條件下的環空壓力瞬態變化曲線

圖11～圖13分別為氣侵初期井深4 170 m處不同地層滲透率、井底負壓差(地層壓力減井底壓力)和井眼尺寸條件下的環空壓力瞬態變化曲線。氣侵初期環空壓力受地層滲透率、井底負壓差和井眼尺寸的影響較大，且隨著地層滲透率和井底負壓差的增加，以及井眼尺寸的減小，水錘現象更加顯著，水錘壓力波動振幅增加，水錘壓力增量也增大，氣液交界面上升至該位置的時間減少，但水錘壓力波動頻率基本一致。隨著地層滲透率和井底負壓差的增加，及井眼尺寸的減小，瞬態氣侵速率增加而瞬態氣侵時間變化較小綜合作用所導致的結果，見表1。當氣液交界面向上運移超過4 170 m后，隨著地層滲透率和井底負壓差的增加，以及井眼尺寸的減小，該處的環空壓力下降速度增大。

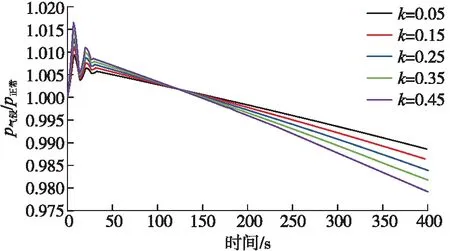
圖11 不同地層滲透率條件下環空壓力隨時間的變化曲線

圖12 不同井底負壓差條件下環空壓力隨時間的變化曲線

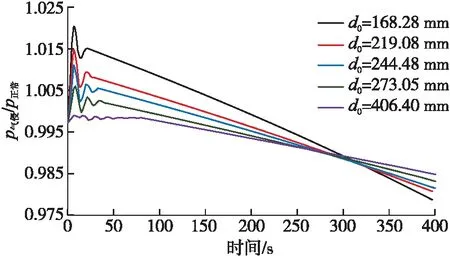
圖13 不同井眼尺寸條件下環空壓力隨時間的變化曲線

表1 不同敏感性參數條件下的瞬態氣侵速率和瞬態氣侵時間

6 結論

(1)考慮了氣侵初期的水錘效應，建立了水錘—漂移流綜合模型來描述氣侵過程中環空壓力的瞬態變化規律，并提出采用基于Lax-Friedrichs格式和MacCormack格式的復合差分格式對該模型進行了求解。

(2)氣侵發生初期，由于地層氣體迅速進入井筒導致鉆井液柱產生水錘效應，氣液交界面以上鉆井液柱的環空壓力增加并隨時間周期性波動，波動振幅隨時間逐漸減小；氣液交界面以下的兩相流區域內的環空壓力隨時間近似線性降低。

(3)水錘壓力波動振幅隨瞬態氣侵速率的增加和瞬態氣侵時間的減少而增大，而波動頻率僅隨瞬態氣侵時間的減少而增大。地層滲透率、井底負壓差越大，井眼尺寸越小，則瞬態氣侵速率越大，氣侵初期的水錘效應越顯著，且兩相流區域內的井底壓力下降速度越快。

(4)從尖北地區一口實鉆井來看，氣侵初期氣液交界面以上不同井深處的相對環空壓力比近似相等，且隨著井深的減小，氣液交界面上升至相應位置的時間增加，因此環空壓力開始降低的時間也增加。這可以作為氣液交界面位置追蹤的依據，且不同時間段內不同井深處的相對環空壓力比之間的一致性和差異性為多測點早期氣侵檢測提供了理論依據。