美妙的特征數

■李大順

特征數指的是眾數、中位數、平均數、百分位數、標準差或方差,為了從整體上更好地把握總體的規律,通過對樣本數據的研究來比較全面地認識和估計總體,進而使我們能從整體上更好地把握總體的規律、對總體作出合理的推斷與決策,初步體會、領悟“用數據說話”的統計思想方法。

一、眾數

例1 某班50名學生的一次安全知識競賽成績分布如表1所示(滿分10分)。

表1

這次安全知識競賽成績的眾數是( )。

A.10 B.9

C.8 D.6

眾數是一組數據中出現次數最多的數。由表中數據可知,成績9分出現的次數最多,所以眾數是9。應選B。

評注:眾數就是樣本數據中出現次數最多的那個數。眾數可以有兩個或兩個以上。

二、中位數

例2 某校舉行“社會主義核心價值觀”演講比賽,學校對30名參賽選手的成績進行了分組統計,結果如表2所示。

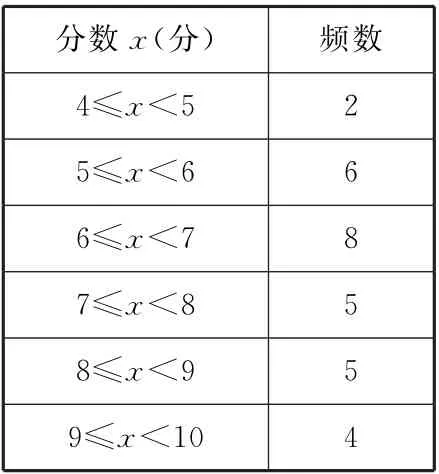
表2

由上可知,參賽選手分數的中位數所在的分數段為( )。

A.5≤x<6 B.6≤x<7

C.7≤x<8 D.8≤x<9

已知數據共有30 個數,中位數是第15,16個數的平均數,而第15,16個數所在分數段均為6≤x<7,所以參賽選手分數的中位數所在的分數段為6≤x<7。應選B。

評注:中位數是一組數據按大小順序排列后,處于中間位置的數。如果這組數據是偶數,則取中間兩個數據的平均數即為中位數。

三、平均數

例3 期中考試后,班長算出全班40名同學的數學成績的平均分為M,如果把M當成一個同學的分數,再與原來的40個分數一起,算出這41 個同學的平均分為N,那么M∶N=( )。

評注:平均數是樣本數據的重要數字特征,平均數越大表明數據的平均水平越高,平均數越小表明數據的平均水平越低。由于平均數與每一個樣本數據有關,所以任何一個樣本數據的改變都會引起平均數的改變,這是中位數、眾數都不具有的性質。

四、百分位數

例4 一個容量為20的樣本,其數據按從小到大的順序排列為1,2,2,3,5,6,6,7,8,8,9,10,13,13,14,15,17,17,18,18,則該組數據的第75 百分位數為____,第86 百分位數為____。

因 為50% ×8=4,所 以50%分位數是(x+17)÷2=16,解得x=15。

因為75%×8=6,所以75%分位數是(y+22)÷2=20,解得y=18。

評注:計算一組n個數據的第p百分位數的三個步驟:第1步,按從小到大排列原始數據;第2步,計算i=n×p%;第3步,若i不是整數,而大于i的比鄰整數為j,則第p百分位數為第j項數據,若i是整數,則第p百分位數為第i項與第(i+1)項數據的平均數。

五、方差或標準差

例6 樣本中共有5個個體,其值分別為a,0,1,2,3。若該樣本的平均數為1,則樣本方差為( )。

評注:方差或標準差是描述一組數據的波動性大小,方差或標準差越小,這組數據越穩定。

六、特征數的綜合運用

評注:理解平均數,中位數,方差或標準差的含義是解題的關鍵。

1.一組觀察值4,3,5,6出現的次數分別是3,2,4,2,則樣本平均數為( )。

A.4.55 B.4.5

C.12.5 D.1.64

2.從某公司生產的產品中,任意抽取12件,得到它們的質量(單位:kg)如下:

7.9,9,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8。

求這組數據的四分位數。

提示:這組數據按照從小到大的順序排列為7.8,7.9,8,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9,9.9。