核心素養視角下培養初中學生幾何推理能力的方法

謝競輝

【摘要】作為初中數學的主要內容，幾何推理能力可有效強化學生的抽象思維，進而為其提高素養，以及日后的學習，做好鋪墊。基于此，本文將主要分析如何在核心素養下，培養學生的幾何推理能力。

【關鍵詞】初中數學;核心素養;幾何推理能力;培養方法

教師在實際教學中，常常不知道該怎樣培養學生的幾何能力，所以學生在學習中，幾乎都是憑借自身的抽象思維，而進行學習，但是初中生的差異很大，并不能夠加強自己的幾何能力，這對于提高教學效果來說，是非常不利的。為有效解決上述這一情況，教師積極培養學生的幾何推理能力，進而確保他們能夠有效了解幾何知識。

一、探究分解圖形，演繹論證推理

核心素養是思維、情感等的表現，學生在組織的教學活動中，通過分析數學概念、具體應用，逐漸形成正確的幾何等素養能力。

以下圖習題為例，需要讓學生求出1+2等于多少度？依據圖例，學生可參考平行線性質，進而輔助線創建內錯角，求得解。

如圖所示，學生作輔助線創建內錯角過E 作 EF ∥ AB，∵ EF ∥ AB，∴ ∠1 = MEF。∵ AB∥CD，∵ EF∥AB，∴ EF∥CD，∴∠2 = ∠NEF。∵ ∠MEF + ∠NEF = ∠MEN = 90°，∴ ∠1 + ∠2 = 90°。結合平行線的性質，求出正解。

在整理幾何推理解題思路的時候，教師需要給予學生足夠的時間，以供他們進行觀察，指引學生結合題目中的文字圖形，思考圖形位置關系，并進行標注，做好輔助線，讓學生通過幾何直觀分析問題，在形成解題思路的同時，提高推理的嚴謹性，從而在最大程度上增強自身的邏輯能力。

二、聯想交流探析，類比歸納推理

處在初中階段時期的學生，正是思維發展的黃金時期，教師應深入挖掘學生的內在潛力，指引其學會從本質出發，鼓勵他們通過類比對象的相似屬性加以分析，推導出正解，以此促使學生在解題過程中，形成全新的概念。因為初中生的認知并不豐富，常常難以自己獨立解決，這時教師可按照他們的水平，為其提供交流空間，進而使學生在推理的過程中，不斷活躍思維，得以在最快時間內發現知識間的內在聯系。

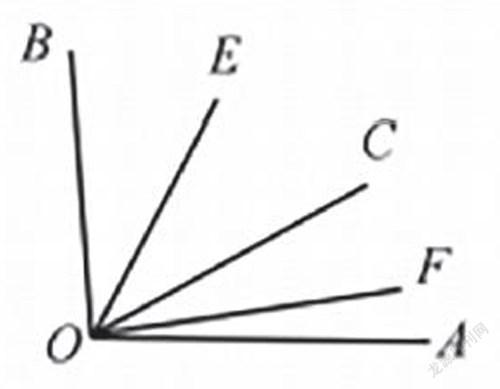
例如，已知∠AOB 內部三條射線為： OE、OC、OF，OE 平分 ∠BOC，OF 平 分 ∠AOC. 若 ∠AOC是 30°，∠BOC 是 60°，那么∠EOF = 45°; 若∠AOC 是α，∠BOC 是β，那么∠EOF = α + β/2 ; 若∠AOB = θ，讓學生按照圖形，想出∠EOF 與 θ 的關系，并要求他們分享出推導的過程。

如圖，學生需要從給出的條件出發，∠EOF = 12 θ. 解題理由： 由于OE 平分∠BOC，OF 平分∠AOC，所以∠EOC = 1/2∠BOC， ∠COF = 1/2 ∠AOC，∠EOF = ∠EOC + ∠COF = 1/2 ∠BOC + 1/2 （∠BOC + ∠AOC）= 1/2 ∠AOB = 1/2θ。角的平分線，可把整體分成兩個相等的部分，學生通過線段中點相似性質類比解決，極大的增強了解題效率。

三、幾何表達轉換，自然描述推理

在核心素養視域下，教師若是想有效培養學生的幾何推理能力，就需要提高他們對性質的理解，指引其借助幾何語言，對問題展開描述性的推理，進而使學生在這一過程中，通過抽象思維，以假設為基礎，充分了解概念的前提下，根據圖形進行解題。因為幾何有著很強的抽象性，初中生在剛接觸時難免會感到手足無措，這時教師應針對性的指引學生進行理解，使其能夠逐漸了解幾何語言，為了在最大程度上增強教學效率，以及促使學生們明確幾何表達方式，教師就可讓他們多去體驗概念，以此進一步加深每一位學生的理解，并在幾何推理過程中，將相關圖形表達出來，同時應用運算推理能力，推理出幾何概念。

例如，在△ABC 中，AB = AC，AD 是 BC 的中線，BE⊥AC 于E。需要求證： ∠CBE = ∠BAD。

學生在進行解題的時候，可聯系——等腰三角形三線合一的性質，來進行推導。∵ 在△ABC 中，AB = AC，∴ △ABC 是等腰三角形，∠ABC = ∠C。又∵△AD是BC的中線，△ABC 是等腰三角形，∴ AD⊥BC，∴ ∠BAD + ∠ABC = 90°。又∵ BE ⊥AC，∴ ∠CBE + ∠C = 90°。又∵ ∠ABC = ∠C，∴ ∠CBE = ∠BAD。

在進行推理過程中，教師要指引學生規范解題格式，使其可了解到相關概念，再用幾何語言展開推導，從而在最大程度上增強學生們的邏輯思維。

四、培養學生空間觀念

在過去的教學模式中，有很多教師常常忽略學生們的幾何推理能力，使學生無法產生出興趣，不僅阻礙了教學進度，還不利于學生發展。我們都知道，興趣是學生最好的老師，尤其是對初中生而言，其可以有效的將興趣轉化為學習的動力。基于此，教師應著重調起學生們的學習熱情，使其在學習的同時，發展自身的幾何推理意識。并且還要按照相關教學內容，提高學生的空間觀念，以及幾何圖形推理能力，進而為之后的學習做好鋪墊。

例如，教師在教學《探索直線平行線的條件》的時候，就可讓學生們通過三角板、直尺等進行學習。在此基礎之上，需要學生對平行線的判定方式，有大致的認知，可用幾何語言進行描述，以此在最大程度上加強每一位學生的能力。為實現上述目標，教師可整合相關例題，在完成教學后，給予學生足夠的思考時間，歸納知識，然后教師再設計習題，促使學生在實際應用的時候，可加深自己的理解，以及提高他們對空間的認知，這樣一來，就會極大的增強學生數學素養。

五、培養學生推論能力

當學生具備空間能力后，教師就可指引他們進行空間推理，使其在知行合一過程中，形成思維能力，以及推論能力。為實現上述目標，教師需創新教學方法，使其緊跟教師思路，仔細完成任務的同時，提高自身的推論能力。

例如，在組織學習《三角形》這一章節的時候，學生需清楚三角形內角和的證明過程。對此，教師可先設置懸疑：為什么三角形的內角和是180°？又該怎么樣去證明呢？通過創設問題，可充分激起每一位學生的探究欲望，提高自身的推論能力。然后教師可采用啟發的形式，讓學生體會推理過程，加深對三角形性質的理解，進而可以做到靈活應用。應用相同的方法，教師可繼續進行三角形外角和的證明教學，促使其在自主探究中，發展幾何推理能力。為使學生的知識更牢靠，教師可適當的舉出一些例子，讓學生在具體應用的時候，檢查成果，從而在最大程度上提高學生們的能力，強化數學素養。

六、指引學生解答幾何題目

完成培養學生的幾何推理能力后，教師可為其設置幾何題目。在這一過程中，教師需重視題目的難易性，以此保障學生可在自身的認知范圍內，展開解答。若是題目過難，學生在嘗試無果后，很容易想要放棄，這樣一來，就會降低他們的積極性;而題目要是太簡單的話，學生不用怎么思考就能求出正解，那也就喪失了意義，又何談培養學生的幾何推理能力呢？并且學生們還會逐漸產生一種盲目的自信，這對于學習而言，有著非常嚴重的影響。對此，教師在訓練的時候，一定要合理把控難度。

例如，在學習《弧長及扇形面積》時，學生需應用推理的方式，推導出計算公式，進而發展自己的幾何推理能力。為實現這一目標，教師應積極指引每一位需熱身，并為其篩選一些得當的題目，以此加深每個人的理解，從而在最大程度上增強每一位學生的數學能力，促使其素養的提高。

總的來說，基于核心素養要求，教師應在初中教學活動中，注重培養學生們的能力，這樣一來，既可以活躍他們的思維，提高效率，還能夠激起他們的應用意識，加深對性質的理解，進而為其之后的學習做好鋪墊。

【參考文獻】

[1]馬麗娜.巧設問題 激活思維[J].初中數學教與學，2020（18）.

[2]劉世云.關于初中數學幾何推理和圖形證明策略的分析[J].學周刊，2016（01）.

[3]葛瑩.初中數學幾何推理與圖形證明對策[J].學周刊，2015（14）.

[4]李拓.初中學生幾何推理能力的培養策略[J].中華少年，2017（33）.

[5]朱月祥，周偉偉.淺談在幾何入門階段培養初中生的推理能力[J].中學數學教學參考，2015（Z3）.

[6]胥秀珍.初中生幾何邏輯推理能力培養的“三步曲”[J].理科考試研究，2014（10）.

（責任編輯：洪冬梅）