π介子譜的電荷依賴性

張 勇，丁慧強，王詩瑤

（1.江蘇理工學院 數理學院，江蘇 常州 213001；2.大連理工大學 物理學院，遼寧 大連 116024）

高能重離子碰撞早期所產生的致密物質的性質一直備受研究者關注。碰撞所產生的系統時空尺度極小（系統壽命約為10-24秒量級，系統空間尺度約為10-15米量級），當前無法直接探測碰撞所產生物質的性質，只能通過分析觀測到的末態粒子信息，還原碰撞產生的系統演化情況及各階段的物理性質。

粒子的橫動量譜是高能重離子碰撞中重要的末態可觀測量，它被用來研究碰撞所產生系統的熱化及膨脹[1-4]。研究表明，化學凍出后的粒子受到介質效應會發生質量偏移，從而對粒子的動量譜產生影響。之前，筆者研究了質量偏移對φ介子譜的影響，得知由于φ介子的反粒子是其自身，因此正反φ介子處于介質中的質量相等[5]。帶電粒子與其相對應的反粒子同介質的相互作用是不同的，因此介質中帶正電粒子的質量與帶負電反粒子的質量不相等[6-12]。介質中正反粒子的質量差異可能會導致其粒子動量譜的不同，因此有必要進一步深入研究。

高能重離子碰撞產生的帶電粒子的凈電荷數是實驗和理論界十分關注的觀測量，目前人們利用凈電荷數對碰撞能量的依賴關系來研究碰撞產生致密物質的相變臨界點。在高能重離子碰撞中，π介子的產額是最大的，因此帶電的正反π介子粒子數的差異對凈電荷數的貢獻就非常大。按所帶電荷性質的不同，π介子可以分為帶正電的π+、帶負電的π-及電中性的π0。真空中π+和π-的質量相等，都是139 MeV；π0的質量比前兩者略小，為135 MeV[13]；其中，π+和π-互為反粒子，π0的反粒子是其自身。π0對凈電荷數是沒有貢獻的，因此本文只研究介質質量差異對π+和π-動量譜的影響。

1 基本公式及研究方法

1.1 基本公式

定義a′?k和a′k分別為處于介質中動量為k的正粒子的產生算符和湮滅算符，定義b′?k和b′k分別為處于介質中動量為k的反粒子的產生算符和湮滅算符。介質中正反粒子由于電荷差異會受到不同的介質效應，因此它們在介質中的能量不相等。假設介質中正反粒子的能量差異為2δ，則自由粒子的產生算符（）與湮滅算符（ak、bk）與介質中準粒子的產生算符（）與湮滅算符（a′k、b′k）可以由波戈留波夫變換聯系起來[14]，見式（3）～（7）：

介質中正反粒子的質量分別表達為式（8）和（9）：

公式（8）、（9）中的m′為當δ=0時正反粒子處于介質中的質量。對于一對正反粒子，m′a表示的是介質中質量較大的粒子，m′b表示的是另一粒子。

歐洲的大型強子對撞機所實現的對撞能量較高，對撞產生的系統會在極短時間內（約0.5 fm/c）達到局域平衡。達到局域平衡后，系統的演化理論上可由相對論流體力學來描述。對于流體力學演化源，正反粒子的動量譜[14]可由式（10）～（14）計算：

由于本文所研究的對象是π介子，因此n′a,k′，n′b,k′的形式為玻色分布，見式（15）和（16）：

公式（10）和（11）中的gi是標號i強子的簡并因子，d4σμ(r)為四維流體凍出曲面元。公式（13）～（16）中的uμ(r)和T(r)分別為動力學凍出點的四速度和溫度；為粒子的四動量，是局域系下的量，對應質心系的量為。π0的反粒子是其自身，因此正反π0處于介質中的質量相同（δ=0），Na(k)=Nb(k)；π+和π-互為反粒子，此時正反粒子處于介質中的質量不同（能量差異δ>0），因此Na(k)≠Nb(k)。

1.2 研究方法

在本研究中，粒子發射源的空間分布采用球對稱高斯型[15]，見式（17）：

式中，C為歸一化因子，R是粒子發射源的半徑參數。粒子發射源的膨脹速度取如下形式[15]，見式（18）：

式中h為速度參量。采用粒子瞬時凍出假設[15]，正反粒子的動量譜可改寫為式（19）與（20）：

當速度參量h、發射源半徑參數R、π介子凍出溫度等相關物理量確定后，可利用公式（19）、（20）計算正反π介子的粒子譜。在計算中，π介子凍出溫度選取130 MeV，粒子發射源的半徑R取5 fm（高能重離子碰撞中金核-金核對心碰撞和鉛核-鉛核對心碰撞所產生系統的半徑約為5 fm）。

2 結果

圖1展示了偏移質量相等時（δ=0）正反π介子的橫動量譜。δ=0時，π+和π-的粒子譜相同，因此圖1中的譜表示的是π+或π-的動量譜。圖中的橫坐標k T為橫向動量（實驗測量π介子譜時，通常以橫向動量為變量作圖），圖1（a）為靜態源的結果（h=0），圖1（b）為源膨脹速度h=0.5時的結果。其中，黑色實線表示的是沒有質量偏移時的結果，彩色虛線表示有質量偏移時的結果，圖中的δm=m′-m。結果表明，質量偏移效應會提升大橫動量區域的π介子產額，這種效應隨著偏移質量δm的增加而增加，但隨著源膨脹速度的增加而減小。

圖2為偏移質量不等時正反π介子的橫動量譜，此時的源膨脹速度h=0.5。圖中，Na表示介質中質量較大π介子的動量譜，Nb表示介質中質量較小π介子的動量譜。結果表明，當偏移質量不等時，正反π介子的橫動量譜出現差異，并且這種差異隨著正反π介子質量差異的增大而增大。

圖1 偏移質量相等時正反π介子的橫動量譜

圖2 偏移質量不等時正反π介子的橫動量譜

為了定量地研究正反π介子橫動量譜之間的差異，定義如下參量，見式（21）：

從公式（21）可以看出，F可以定量地反映出正反π介子橫動量譜之間的差異。

圖3展示了F隨δm和δ變化的三維圖。其中，圖3（a）、3（b）表示橫動量為0.8 GeV/c的結果；圖3（c）、3（d）表示橫動量為1.6 GeV/c的結果；圖3（e）、3（f）表示橫動量為2.4 GeV/c的結果；圖3（a）、3（c）、3（e）為源膨脹速度h=0.3時的結果；圖3（b）、3（d）、3（f）為源膨脹速度h=0.5時的結果。從圖中可以看出，正反π介子橫動量譜之間的差異隨著δ增加而變大。在小橫動量區域，δm對正反π介子橫動量譜之間的差異沒有明顯影響，見圖3（a）、3（b）。在大橫動量區域，正反π介子橫動量譜之間的差異隨著δm的增大而減小，表現出一定的依賴關系；這種依賴關系隨著橫動量的增大而變大，但隨著源膨脹速度的增加而減小，通過比較圖3（c）、3（d）、3（e）、3（f）可以看出。

圖3 參量F隨δm和δ變化的三維圖

圖4展示了參量F隨著橫動量和δ變化的三維圖。圖4（a）、4（b）表示δm=5 MeV時的結果；圖4（c）、4（d）表示δm=10 MeV時的結果；圖4（a）、4（c）表示h=0.3時的結果；圖4（b）、4（d）表示h=0.5時的結果。從圖中可以看出：在小橫動量區域（小于1.5 GeV/c），正反π介子橫動量譜之間的差異與源膨脹速度、δm以及橫動量無關；在大橫動量區域，正反π介子橫動量譜之間的差異隨著動量的增加而減小，這種依賴關系隨著源膨脹速度的增加而減小。

圖4 參量F隨橫動量和δ變化的三維圖

圖5為參量F隨著橫動量變化的二維圖。其中，圖5（a）為δm=5 MeV時的結果，圖5（b）為δm=10 MeV時的結果。從圖中可以看出，在大橫動量區域（大于1.5 GeV/c）正反π介子橫動量譜之間的差異與橫動量存在依賴關系，并且這種依賴關系隨著源膨脹速度的增加而減小。

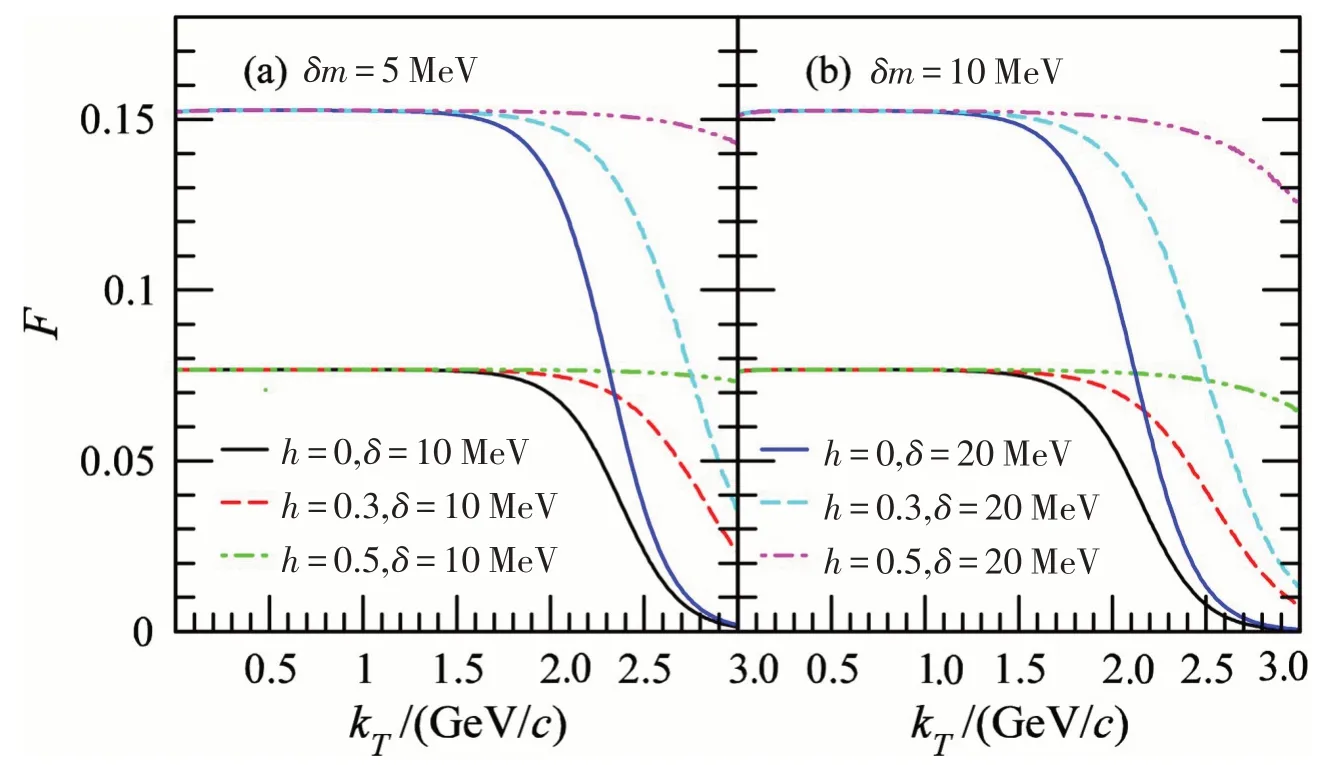
圖5參量F隨橫動量變化的二維圖

近年來，高能重離子碰撞所產生粒子的凈電荷數（核-核碰撞所產生的帶正電的粒子數目減去帶負電的粒子數目即為凈電荷數）是實驗和理論界都在關注的重要觀測量。π介子是每次核-核碰撞所產生的帶電粒子中數量最多的，因此正反π介子粒子數的差異對凈電荷數的影響是可觀的。圖2~圖5的結果表明，由介質效應造成的正反π介子的介質質量差異會導致正反π介子動量譜產生差異，從而導致正反π介子粒子數出現差異，并進一步影響帶電粒子的凈電荷數。

3 總結

粒子的橫動量譜是高能重離子碰撞中重要的末態可觀測量。化學凍出后的粒子受到介質效應會發生質量偏移，從而對粒子的動量譜產生影響。正反帶電π介子的電荷存在差異，其與高能重離子碰撞所產生環境的相互作用是不一致的，因此介質中正反帶電π介子的質量不相等。本文研究了介質中正反π介子質量差異對其動量譜的影響，結果表明：正反π介子介質質量差異會導致正反π介子動量譜存在差異，出現電荷依賴；正反π介子譜的差異隨著介質質量差異的增大而增大；在小橫動量區域，正反π介子譜的差異對源膨脹速度和橫向動量沒有依賴性；在大橫動量區域，正反π介子譜的差異隨著橫動量的增加而減小，但隨著源膨脹速度的增加而增大。

高能重離子碰撞所產生帶電粒子的凈電荷數是目前實驗和理論界十分關注的觀測量，人們利用凈電荷數隨碰撞能量的依賴關系來研究碰撞所產生致密物質的相變臨界點。π介子是每次核-核碰撞所產生帶電粒子中數量最多的，因此正反π介子粒子數的差異對凈電荷數的影響是可觀的。本文研究表明，正反π介子的介質質量差異會導致正反π介子動量譜產生差異，并進一步影響帶電粒子的凈電荷數。因此，在計算π介子動量譜時需要考慮正反π介子介質質量差異的影響。