Measuring gravitational effect of superintense laser by spin-squeezed Bose–Einstein condensates interferometer

Eng Boon Ng and C.H.Raymond Ooi

Department of Physics,University of Malaya,Kuala Lumpur 50603,Malaysia

Keywords: intense laser field,atom interferometer,Bose–Einstein condensates,spin-squeezing

1. Introduction

This high sensitivity has made the atom interferometer a potential tool to reveal the gravitational effect from an intense laser. Observable gravitational effect is always generated by bodies of large masses. However, the source of the gravitational field can also come from the electromagnetic field.[5]Laser,composed of varying electromagnetic fields,is another excellent tool to study gravity on a small scale. It has been predicted laser intensity up to 1021W/cm2is able to curve the spacetime and produce artificial gravity.[6]

With the technological prowess and efforts put in by scientists, particularly the ELI group, a high-power laser with peak power of more than 1015W has been invented.[7]By packing energy to a very short lifetime,the power of the laser can be boosted up extremely. Petawatt laser is becoming common because of the technique called chirped-pulse amplification(CPA),[8]which breaks the light pulse into components and amplifies them individually before rejoining them back together. Currently,high-power laser system(HPLS)designed by ELI can create extremely intense pulse[9]with intensity reaching 1023W/cm2. Powerful pulse amplification technique such as optical parametric chirped pulse amplification(OPCPA), an extended version of CPA, has been designed to compress the laser pulse to sub-fs duration.[9]In this method,a pump beam is used to amplify the signal beam in the OPCPA.

For creating a laser with intensity exceeding 1023W/cm2,plasma compression of laser pulse using backward Raman scattering[10]is suggested. The interactions of three waves,including pump pulse withωa,seed pulse withωband plasma wave withωp=ωa-ωb,cause an energy transfer from pump pulse to seed pulse.[11]The seed pulse produced after CPA and OPCPA can be amplified to femtosecond pulse by using backward Raman scattering. By using this three-step pulse amplification method, better known as cascaded conversion compression,[12]an ambitious but realistic plan to create the exawatt laser[13,14]is now possible. Thus, a laser with an intensity of 1025W/cm2is likely to be achieved within the next few years.

Inspired by the idea of high-intensity laser, we aim to study the gravitational effect of high-intensity laser[6,15–17]with the help of an atom interferometer in our paper.The gravitational properties of laser have been explored by.[18–20]The weak gravitational field produced by the laser can be modelled in the framework of linearized gravity. To detect it,we design an atomic interferometer scheme loaded with Bose–Einstein condensate (BEC). To further enhance the sensitivity, tripod scheme is applied to the BEC to produce spin squeezing effect.

2. Gravitational potential

We first compute the gravitational potential from the intense laser. With considering a high-intensity laser beam with radius,rl,traveling along thez-axis,its electric and magnetic fields oscillating along thexandydirections,respectively,can be written as

The laser parameters we considered produce high power in the petawatt range. The pulse of the laser with pulse energy of 2 kJ is compressed to 1 ps to produce the high-power laser pulse.[9,25,26]The beam size isrl=10 μm so the intensity of the laser is about 1021W/cm2. Besides, we also consider the exawatt laser with power in the range of 1018W by increasing the pulse energy to 2 MJ. The intensity we considered is 1024W/cm2.The exawatt laser and zettawatt laser are possible to realize according to Ref. [13] and the exawatt laser is currently under construction. From the laser parameters, the average force per atom can be estimated to giveFg ≈10-42N or acceleration,δg=10-19gfor petawatt laser,andFg ≈10-39N orδg= 10-16gfor exawatt laser. For petawatt laser, the strength of acceleration produced by the linearly polarized Gaussian pulse is consistent with the circularly-polarized laser pulse in Ref.[19].

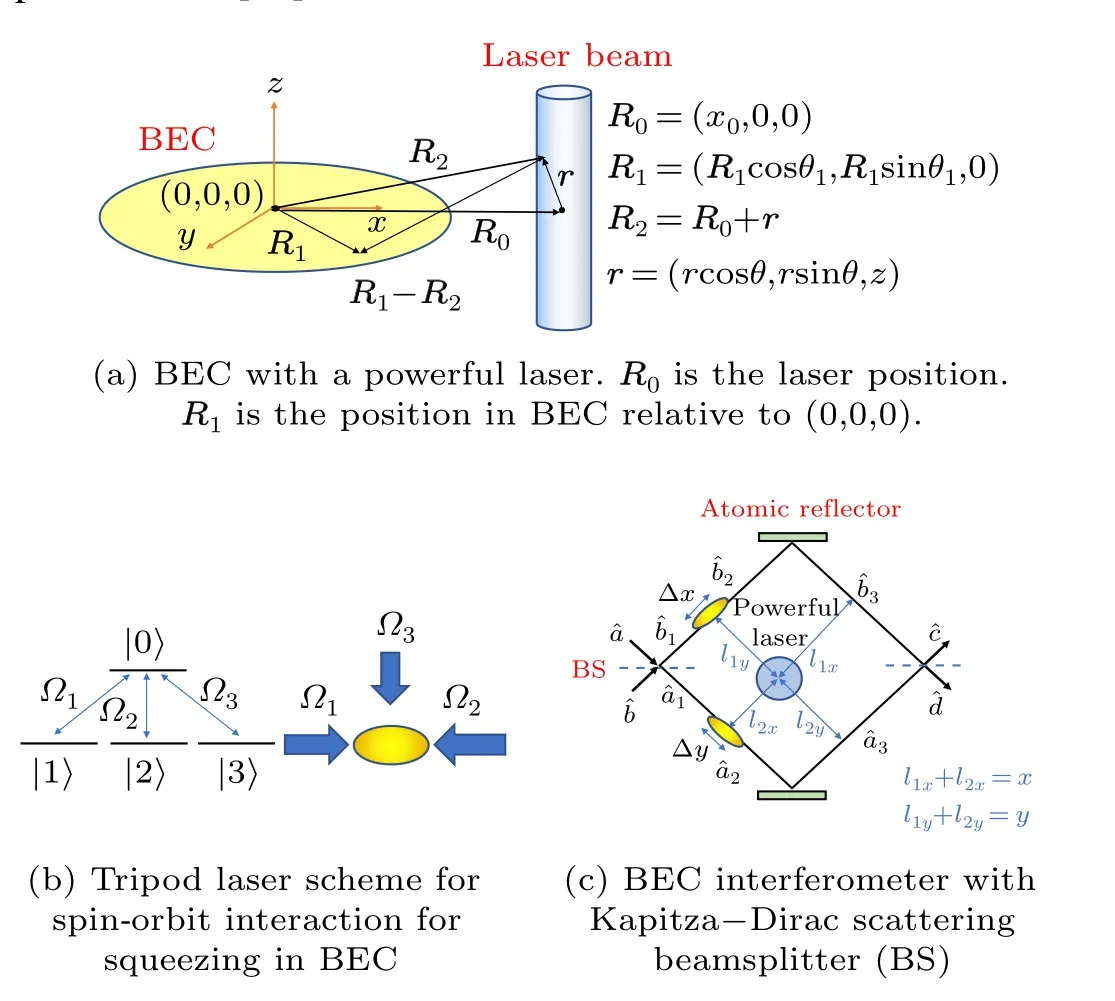
Fig.1.(a)Vector coordinates in BEC and a powerful laser.(b)Tripod scheme acting on the BEC creating spin-squeezing effect is created at the beginning of the path, Δx and Δy. Ωi is the Rabi frequency of the laser to couple the internal state of the BEC. (c) Schematic of a spin-squeezed BEC interferometer. The laser beam is placed near the lower path of the interferometer,x0 =0.5 mm. Optical standing wave acts as beam splitter(blue dotted line)and mirror(red line)for the BEC.Circle at center represents the gravitational source at(x0,y0),is allowed to vary along the arm length of the interferometer, l1x+l2x. The gravitational force is perpendicular to the arm, inducing a phase shift in the BEC and affecting the interference fringes at the output.The effect of deflection by the gravitational force is less important than the phases induced on the arms. In practice any deflection can be corrected to avoid a loss of contrast.

3. Atomic interferometer

We are concerned about the strength of the laser parameters to produce gravitational effect,and the possibility to measure the small perturbation. From previous studies,[19]the deflection of test particles by gravity is, in general, too small to be measured. Instead, the phase shift of atoms has been proposed to study the gravity generated from the high-power laser.The interferometric detection method is usually employed to detect the slight phase shift. To produce a measurable phase shift,a long optical traveling path is necessary.[16,27]Besides,by using the collective oscillation, BEC has been suggested to be used as a sensor to detect gravitational wave[28]and oscillating gravitational field.[29]The main advantages of using BEC as a medium in the interferometer are also obvious over the typical ultracold atom. Large coherence length of BEC and narrow velocity distribution give high fringe contrast, better beam-splitting efficiency and large momentum beam-splitting.[4,30,31]BEC in the squeezed state offers a great improvement in signal to noise ratio.[4]

In our case, we demonstrate a BEC interferometer scheme, as illustrated in Fig. 1, to detect the acceleration caused by the intense laser. The optical standing wave,acting as beam splitter or mirror in the interferometer,can manipulate the de-Broglie waves of BEC with different momentum.[32,33]Initially, BEC is split into two groups, approximately 25%of condensate, by letting the BEC passes through the optical standing wave. Diffraction of the atomic wave by the standing wave into momentum states with±ˉhkeffoccurs, which is known as Kapitza–Dirac scattering.[32,33]These two groups of atoms travel to two different paths in the interferometer and undergo free evolution while experiencing the force from the intense laser as well as the geometric phase. Note that the intense laser is entirely enclosed by the interferometer’s arms and is not placed exactly at the center of the interferometer.At timeT,optical standing wave is applied to reflect the BEC.Now, the optical standing wave is considered as two waves traveling opposite to each other.NBphotons are transferred between the two traveling waves, giving rise to a total exchange of momentum, 2NBˉhkefffrom photons to the bosons.This is known as Bragg scattering.[32,33]Finally, after traveling for 2T, these two groups of BEC are recombined coherently. Spatial fringes are formed, revealing the phase difference caused by the acceleration.

In contrast to the conventional Mach–Zehnder interferometer,tripod scheme,[34–37]which has been used in creating spin–orbit coupling effect in ultracold atoms,is applied at the beginning of each path (Δxand Δyin Fig. 1) to generate a non-Abelian gauge field that affects the spin behavior. Three lasers in a particular arrangement couple the degenerate internal states of87Rb, including|1〉,|2〉, and|3〉together, to produce the pseudospin by Rabi frequencies,Ω1=|Ω1|e-iS1,Ω2=|Ω2|e-iS2 andΩ3=|Ω3|e-iS3. After solving the Hamiltonian of the tripod scheme, the dressed states[34,35,37]are given as

Δxand Δyare the length scales where lasers have the strongest intensity[34]to couple the internal states. As mentioned in Ref.[34], the velocity of BEC is generally faster than the recoil velocity,λR=0.5 cm/s. Hence, the non-Abelian gauge field only affects the internal state of the BEC without having any effect on the center of mass dynamics.

Now, we determine the effect of the gauge field on the output of the interferometer. Leta?andb?be the annihilation operators for boson at the two inputs, and the output boson number operators[40](see Appendix B)are

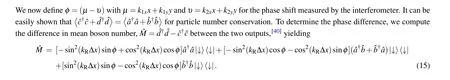
The tripod scheme does contribute to the output number difference. For one input interferometer,〈?a??a〉=Nand〈?b??b〉=0, the phase shift generated by the tripod scheme results in〈M〉=Ncos2(kRΔx) whenφ=0. SincekRand Δxare the values set in experiment,cos2(kRΔx)is merely a constant that can be computed and should not cause any difficulty in measuring the unknownφ. To see how the tripod scheme affects the phase sensitivity, we compute the phase sensitivity equation by

For our interferometer scheme,to enhance the phase sensitivity,the spin properties under the influence of non-Abelian gauge field has to be considered in the phase sensitivity calculation. Previous studies show that the spin–orbit coupling effect[44–46]can lead to spin squeezing, providing an important boost in the phase sensitivity to approach the Heisenberg limit. By reducing the quantum fluctuation of a spin operator in one direction at the expense of the fluctuations in the other two spin operators,precision in the measurement of phase[47]can be significantly enhanced by

after spin rotation. Spin squeezing that can reduce the quantum phase fluctuation by half occurs if 2kRΔx=(π/3)+2nπ.Hence,ξican help improve the sensitivity of phase measurement by one order.

After getting the phase sensitivity of the interferometer,we can proceed to discuss the feasibility of measuring the gravitational effect from the intense laser. To determine the gravitational effect,the point,(x0,y0)in Fig.1 is replaced with intense laser. The gravitational potential from the intense laser is modelled by Eq. (9). For simplicity, we assume the force is always perpendicular to the interferometer arms acting towards the intense laser. The gravitational force of the intense laser imparts an acceleration,δgon the BEC with total mass ofmB=Nmand leads to a small change in phase of BEC,φ. The path traveled by BEC under the influence of gravity can be treated as a perturbation on Lagrangian dynamics.[49]The phase change of BEC is ei(L/ˉh)Δt,whereL=L0+λL1is total Lagrangian,L0is unperturbed Lagrangian andλL1is perturbation Lagrangian with orderλ. Without gravity,L=L0=(mB˙x2)/2, BEC travels along straight line with its phase, ei(L/ˉh)Δtreducing to ei(kx-ωt).[49]Under the influence of gravity,the BEC is attracted toward the laser,and hence the path is deflected slightly. For simplicity, we first assume the acceleration is constant atgwith direction pointing towards a reference point at(x0,y0)where potential energy is zero. The Lagrangian equations with gravity as the perturbation for each arm are given as

Assuming the BEC ofN=105travelling at 0.3 m/s with the interferometer arm’s length equals to 3 mm,Tis about 10ms.By using Eqs. (17) and (23), the smallest change in acceleration that can be detected is estimated atδg=10-15g. The gravitational effect from the petawatt laser is too small to be measured by the interferometer. If exawatt laser can be built,the acceleration is just one order less than the sensitivity of the BEC interferometer. Note thatTcannot be set too high as it will affect the high contrast due to BEC losing its coherence. However, decoherence caused by interaction can be eliminated[50]by tuning the scattering length to almost zero using Feshbach resonance. Therefore,coherence time of BEC reaching 10 s is possible in experiment.[51]

Equation (23) is based on the assumption that the gravitational acceleration due to the laser pulse is present for the whole duration as the BEC travels through the arms of the interferometer. This is necessary for the phase difference along the two paths in the BEC interferometer to accumulate enough so that the gravitational effect can be emerged. However, the effective interaction time for the gravitational potential of the laser pulse to act on the BEC interferometer is extremely short,teff=τ frepT, wherefrepis the repetition rate. So, the actual average acceleration,δˉg=δg×(teff/T)can be computed and shown to be in the order of 10-23gfor exawatt laser withfrep=106Hz. The average acceleration is just too small even when the exawatt laser is measured by the most precise phase measurement device. The power of laser has been improved a lot recently;however,the low repetition rate is one of the main limitations to measure the gravitational effect.

To achieve a high repetition rate,[26]a source with high average power is required. One of the possible methods is the diode laser pumping technology. ELI lasers,which are diodepumped,can produce a laser pulse of 0.1 J energy at repetition rate of kHz.For pulse energy of 1 kJ,the highest rate achieved by HPLS is 1 pulse per minute. Instead of searching for a higher average power source,an alternative is to generate multiple gravitational effects by just a single pulse. Waveguide[52]or ring cavity[53]can be applied to engineer a looping trajectory so that a pulse can repeatedly generate gravitational effect on the atom interferometer. The time for the laser pulse to complete a loop or an oscillation corresponds to the pulse period or the repetition rate of a laser.Recently,an idea of letting short laser pulse oscillating with a high frequency in a cavity is proposed[54]to amplify the power of laser pulse. The power amplification factor up to 103is possible. However,the powerful laser,for example ELI laser,still cannot be used as pump laser in their system because the high power laser pulse can damage the cavity and has a low repetition rate. Nevertheless,the effort of realising the oscillation of high power laser pulse in the cavity brings the hope of creating larger gravitational effect by a single laser pulse.

4. Conclusion

We have derived the gravitational potential of the highintensity laser and designed a spin-squeezed BEC interferometer with improved sensitivity to measure the gravitational effect. The weak attractive force from the gravitational potential can cause a small spatial displacement of the BEC in the interferometer. We determine the laser parameters, which may produce measurable results. The laser parameters we considered are realistic and aligned with the current intense laser development. Even though the gravitational force created by the intense laser is extremely small, it induces variations in the phase of the BEC interferometer. We derive the sensitivity equation of the BEC interferometer to determine the feasibility of detecting the small phase shift. Conventional interferometer is limited by SQL. While other parameters, for example, the number of particles, are subjected to physical limitations,and spin squeezing is the most promising method to improve phase sensitivity below SQL. We create the spin squeezing effect in the BEC interferometer by introducing the non-Abelian gauge field using tripod scheme. Even though the BEC interferometer’s sensitivity and the power of intense laser have been greatly enhanced,the gravitational effect from intense laser remains too small to be measured. The repetition rate and pulse duration determine the effective time of gravitational potential acting on the BEC interferometer. Since these two parameters for the intense laser are extremely low, the phase accumulation in the BEC interferometer is not enough to produce measurable results. An improved design that significantly increases the effective interaction time between the high energy laser pulses and the BEC is needed to achieve a detectable phase shift in the interferometer.

Acknowledgment

R.O. thanks the support by Ministry of Higher Education Malaysia under Long-Term Research Grant Scheme,LRGS/1/2020/UM/01/5/1.

Appendix A

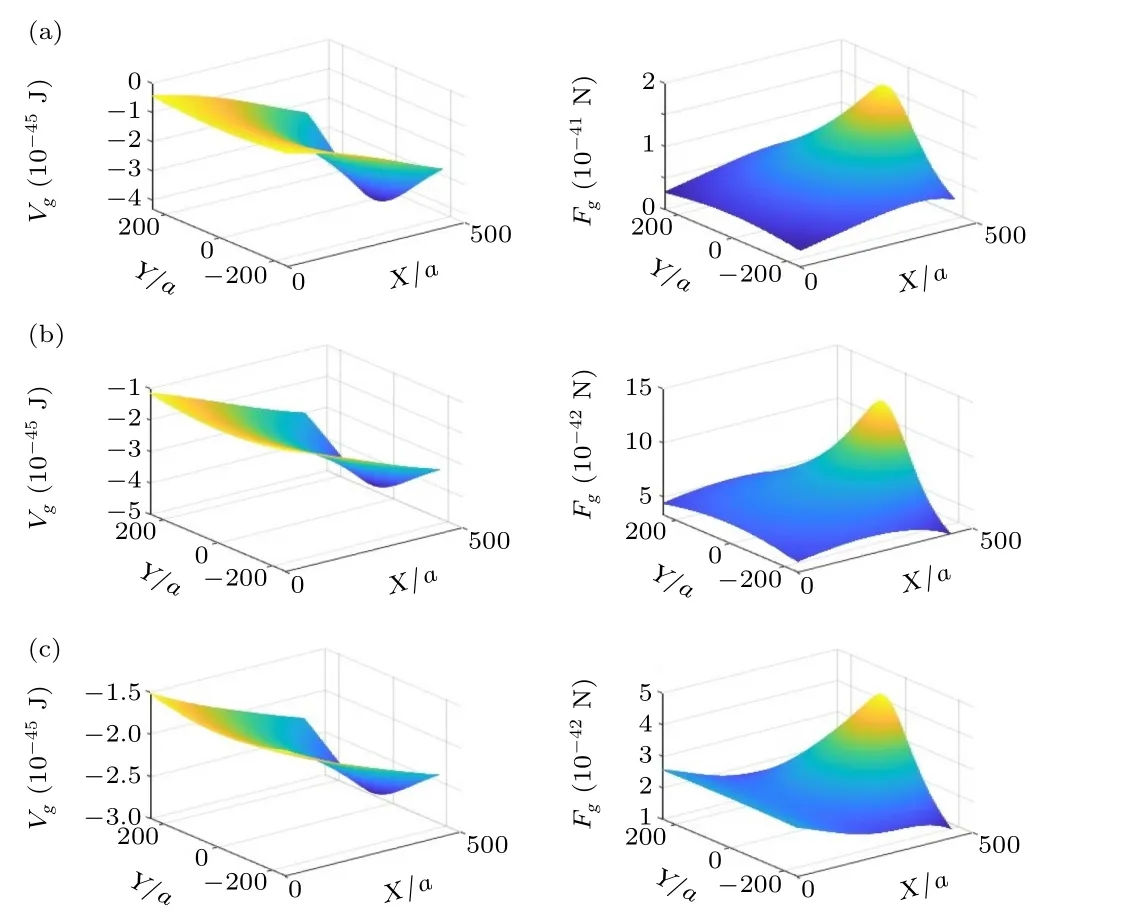
Fig.A1. Gravitational potential(left)from Eq.(9)and force(right)at time,(a)t=0,(b)t=0.5 ps and(c)t=τ=1 ps. We use the parameters: pulse of 2 kJ energy,τ=10-12 s,and beam radius of rl=10 μm. The distance to the beamline is set at x0=0.5 mm and z0=1 mm. Since the radial dependence of Eq. (9) has a Gaussian profile, we cutoff the integration over r at 3rl for Eq.(9). Note that spatial dimensions are reduced by a=9.12×10-7 m.

Fig.A2. (a)Gravitational potential along Y =0 for t=0 to t=τ. The laser parameters used are the same as Fig.A1.

Appendix B

Appendix C