共固化阻尼薄膜夾嵌復合材料梁的振動分析

楊功先，梁 森，王光和，閆云鵬，鄭長升

(青島理工大學 機械與汽車工程學院，山東 青島 266520)

嵌入式共固化復合材料阻尼結構(embedded cocuring composite damping structure，ECCDS)是一種多相固體，由不同性質的3種材料(樹脂、玻璃纖維和黏彈性阻尼材料)通過物理或化學方法復合而成[1-3]。共固化阻尼薄膜夾嵌復合材料梁結構(co-cured damping film sandwiched composite beam structure，CDFSCBS)不僅質量輕、承載強，阻尼性能優良，且更加耐疲勞，減振降噪，在航空、航海與陸地承載等交通運輸領域有廣泛的應用前景。

Zhai等[4-5]基于1階剪切變形理論，探討了在阻尼薄膜復合材料結構中改變黏彈性層參數對結構動力學性能的影響，為其優化結構提供了理論依據。黃志誠等[6]建立了一種新的用于研究黏彈性夾芯梁振動和阻尼特性的有限元模型，該模型同時考慮了黏彈性層的剪切和壓縮阻尼。Filippi等[7]提出了基于Carrera統一公式改進的梁理論的有限元模型，用于夾層梁的振動分析。Nguyen等[8]基于增強型高階分析理論研究了功能梯度夾層板的彎曲、振動及屈曲特性。Jin等[9]基于 Reddy理論分析了單層黏彈性夾層梁的阻尼及振動特性。

Yu等[10]提出了分段剪切變形理論及假設，創建了夾層梁結構的理論模型，并研究了夾層梁在兩端固支邊界條件下的自由振動與熱后屈曲問題。肖龍江等[11]研究了兩端固支邊界條件下具有小初始撓度的屈曲梁在受到基礎簡諧激勵作用時的非線性動力響應。鐘陽等[12]根據辛幾何方法對哈密頓體系下的四邊固支矩形薄板的自由振動進行了求解，并得到精確解。張小廣等[13]對四邊固支功能梯度矩形板在受到橫向簡諧激勵力作用時的非線性主共振問題進行了研究。鮑四元等[14]根據非局部理論，將旋轉約束、橫向位移彈簧引入到梁結構兩端邊界上，并通過設置其剛度的大小來模擬固支邊界條件，得到了梁的固有頻率和陣型曲線。郝芹等[15]根據波傳播法對兩端固支梁在軸向運動時的橫向自由振動進行了分析，得到了梁的模態函數和固有頻率。Ding等[16]構造了一個包含未知系數的應力函數，通過Airy應力函數方法得到了應力與位移的一般表達式，并利用兩端固支邊界條件確定引入應力函數的未知系數，最終得到了兩端固支各向同性材料梁的解析解。

雖然目前國內外很多學者對復合材料層合板、梁結構的振動研究較多，且獲得的成果頗豐。但大多數研究集中在無阻尼、自由阻尼或約束阻尼結構，鮮有文獻對共固化阻尼薄膜夾嵌復合材料固支梁結構動力學性能的研究報道。因此本文基于Hamilton原理、1階剪切變形理論與變分原理，推導出CDFSCBS的應變能、動能以及該結構動力學微分控制方程的表達式，探索出滿足兩端固支邊界條件的位移函數，利用伽遼金加權余值法將CDFSCBS自由振動的偏微分方程轉化為一個齊次線性方程組，從而獲得模型的理論解。運用ANSYS軟件創建阻尼薄膜梁有限元模型，同時制作CDFSCBS試件和所搭建的試驗平臺，進行數值模擬與模態試驗，將模擬結果、試驗結果分別與理論解對比，驗證了理論模型的有效性。在此基礎上進一步探討了阻尼層厚度，上下約束層的比例，以及結構幾何參數對CDFSCBS的動力學性能的影響。

1 基本方程

1.1 基本假設

共固化阻尼薄膜復合材料梁的幾何結構及尺寸，如圖1所示。其面內位移如圖2所示。為了得到結構的振動方程，做出如下假設：

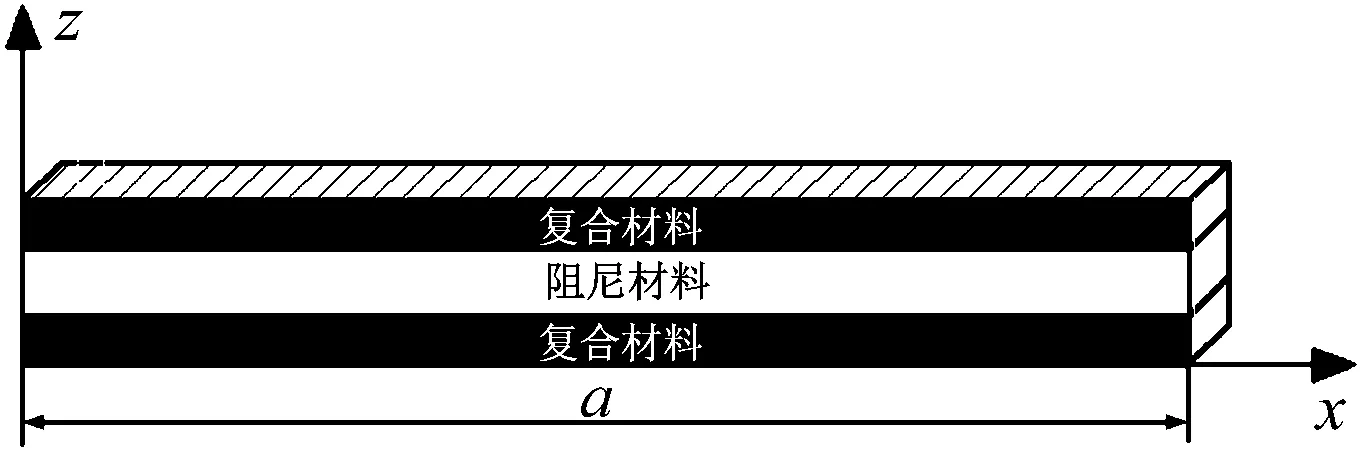
圖1 CDFSCBS的幾何結構

圖2 CDFSCBS的面內位移

(1)嵌入的阻尼層與復合材料層之間的黏結良好，層間變形連續，振動過程中不發生滑移。

(2)結構變形前后，垂直梁面的同一法線上的各點沿厚度方向的位移變化忽略不計。

由于梁結構的跨度遠大于它的寬度和厚度，因此在理論計算中通常將其簡化為一維結構進行理論建模，得到的方程不僅簡單且計算效率較高，接下來對CDFSCBS進行詳細的理論推導。

1.2 阻尼薄膜復合材料梁的本構關系

本文采用考慮剪切變形的鐵木辛柯梁理論，結合所做假設，各層梁的位移模型如下

(1)

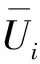
z(i)的意義如圖3所示。在每一層建立獨立的坐標系，并將坐標系的原點設置在每一層的中心線上，因此z方向坐標z(i)的取值范圍為(-hi/2,hi/2)。

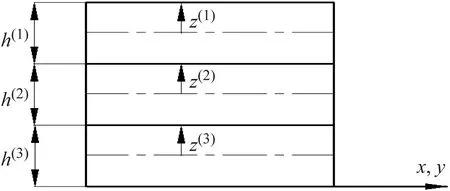
圖3 z(i)的幾何意義

根據式(1)可得第i層梁結構的位移-應變關系表示如下

(2)

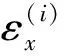
(3)

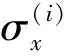
式中，θi為纖維方向與x軸的夾角。

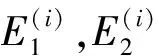
由于黏彈性阻尼層的損耗因子與復合材料層損耗因子相比較大，為計算方便將復合材料層阻尼忽略不計，故實際損耗因子會略高于計算得到的整體損耗因子，因此只對黏彈性阻尼層的剪切模量與彈性模量用常復數模量表示

(4)

式中，n為阻尼層，n=2。

1.3 阻尼薄膜復合材料梁結構的振動方程

對CDFSCBS振動方程的推導過程如下，基于Hamilton變分原理[17]有

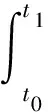
(5)

其中，應變能和動能的表達式如下

(6)

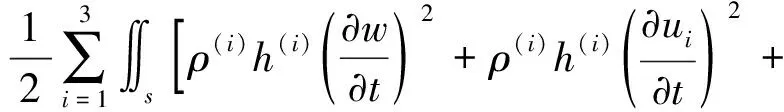
(7)

根據假設(1)，可知中間層的位移為

(8)

這樣可將變量減少到5個，分別是u1,u3,α1,α3和w。

將式(6)和式(7)代入式(5)，結合式(2)、式(3)和式(8)，整理可得阻尼薄膜復合材料梁結構的振動方程，如下

δu1：

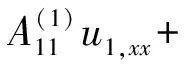
(9)

δu3：

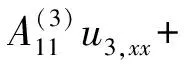
(10)

δw：

(11)

δα1：

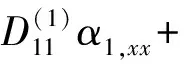
(12)

δα3：

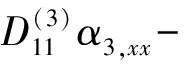
(13)

其中

兩端固支阻尼薄膜復合材料梁的邊界條件為

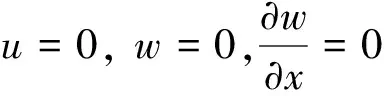
(14)

方程的解可以展開成以下振型函數疊加的形式

(15)

式中，ω*為圓頻率；U1，U3，W，?1和?3為系數。

對于兩端固支邊界條件，振型函數可以采用以下形式

(16)

將式(15)、式(16)代入式(9)～式(13)，并將其展開成以下三角級數疊加的形式

(17)

由伽遼金加權余值的思想可知，三角級數系數應滿足

(18)

根據式(17)與式(18)，可將平衡方程轉化為如下特征值問題

KX=M(ω*)X

(19)

式中：K為整體剛度矩陣；M為整體質量矩陣；X=(U1,U3,W, ?1, ?3)T。

由式(19)、式(20)與式(21)(見文獻[18])計算結構的振動頻率和損耗因子

(20)

η=Im((ω*)2/Re(ω*)2

(21)

2 試驗平臺的搭建與模型驗證

2.1 試驗平臺的搭建

按照碳纖維/環氧預浸料固化工藝曲線制成阻尼薄膜復合材料梁試件，如圖4所示。具體制備工藝參見文獻[19],該試件的幾何參數與材料參數，如表1、表2所示。搭建試驗平臺，如圖5所示。將制作完成的CDFSCBS試件進行模態試驗，試驗平臺包括激勵力錘(型號4524-B004)、加速度傳感器(型號8206-002)、固支夾具、計算機和PULSE(型號3560B)。將3個相同的CDFSCBS試件分別進行試驗，試驗采用單點激勵多點響應的方法對兩端固支CDFSCBS進行模態參數識別，3次激勵數值取平均，3次試驗數據再次取平均，以便獲得較準確的試驗結果。

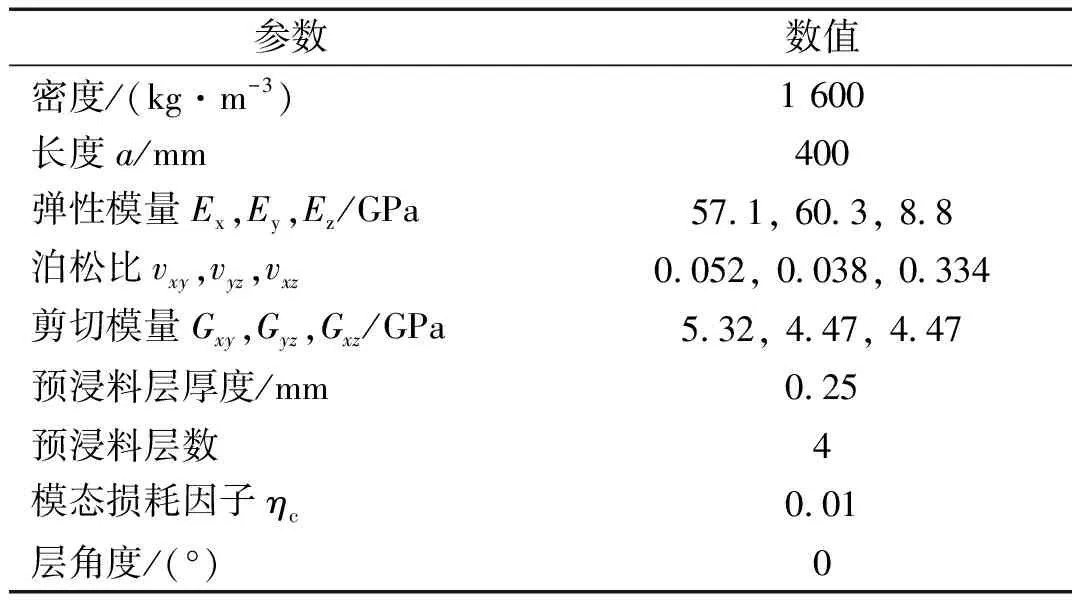
表1 CDFSCBS復合材料層材料參數

表2 CDFSCBS黏彈性層材料參數

圖4 阻尼薄膜復合材料梁試件

(a)

2.2 模型驗證

以無阻尼復合材料層合梁為例，驗證所創建理論模型的有效性。其材料參數為：ρ=1 389.23 kg/m3,E1=144.8 GPa,E2=9.65 GPa，G12=4.14 GPa,G13=4.14 GPa,泊松比v12=0.3；層合梁結構的尺寸為：a=0.381 m，h=a/15；每一層纖維角度為[90°/0°/90°/0°]。表3列出了采用本文方法計算得到的前3階固有頻率與現有文獻數據對比，可以看到良好的一致性。

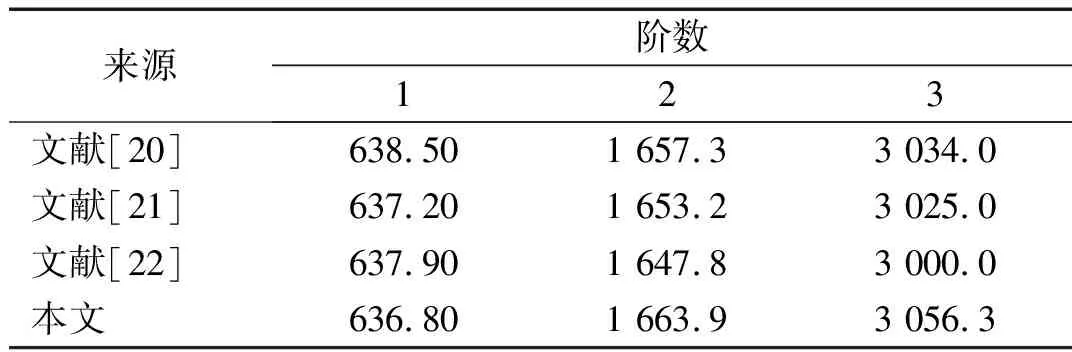
表3 固支邊界條件下復合材料層合梁前3階固有頻率對比

此外，將ANSYS有限元方法、模態試驗方法分別與理論分析方法進行比較。運用ANSYS17.0軟件的Solid Brick 8 node 185單元建立阻尼薄膜復合材料梁模型，各層之間通過共節點連接，設置每一鋪層厚度、鋪設角度、材料參數，具體見表1與表2。

CDFSCBS的損耗因子與前3階固有頻率的理論、試驗、模擬結果對比如表4所示。三者結果基本吻合，誤差均在5%以內，滿足工程應用中需要。其中，誤差1為理論解與ANSYS模擬結果的相對誤差，誤差2為理論解與試驗結果的相對誤差。

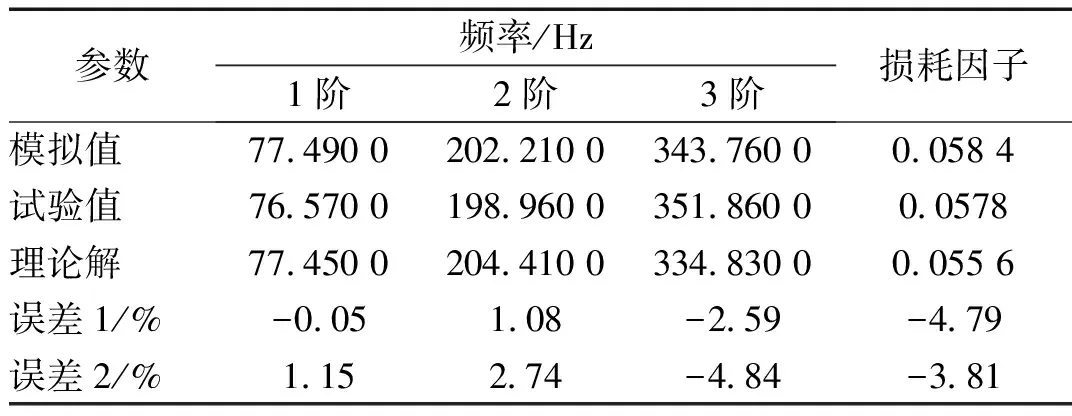
表4 固有頻率和損耗因子計算結果

3 不同參數對CDFSCBS動力學性能影響

在驗證了理論模型正確的基礎上，進一步探討了結構的阻尼層厚度，上下復合材料層比例，阻尼層厚度(Hc)與CDFSCBS的總厚度(H)比，CDFSCBS長度(a)與CDFSCBS的總厚度比對CDFSCBS整體動力學性能的影響。令H=h1+h2+h3，Hc=h2，材料參數見表3。

3.1 結構材料分布對動力學性能的影響

當CDFSCBS上下復合材料層厚度h1+h3=2 mm時，改變黏彈性阻尼層厚度h2的數值，探討h1/h3以及黏彈性阻尼層厚度變化對CDFSCBS的1階頻率與1階模態損耗因子的影響規律，結果如圖6與圖7所示。

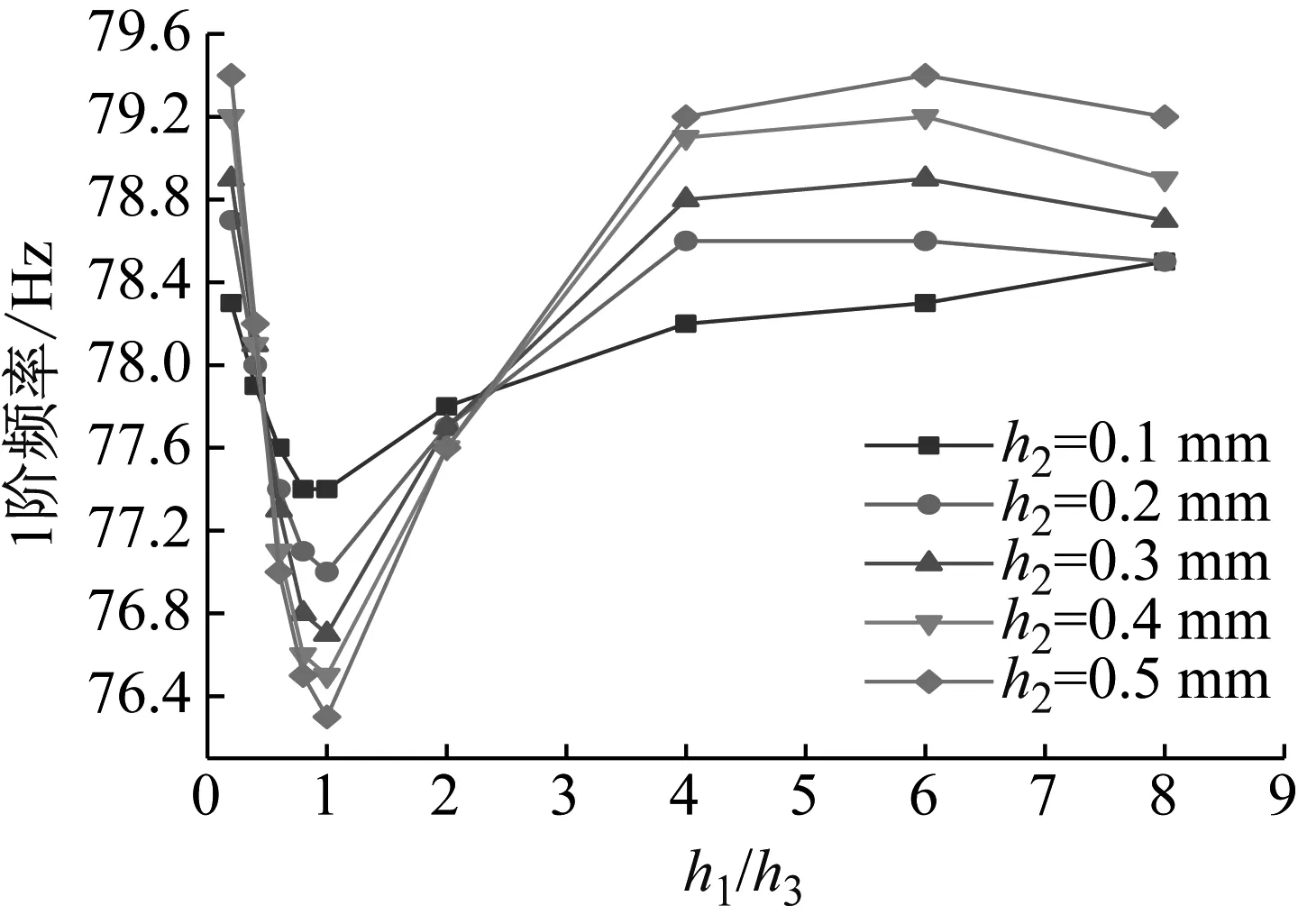
圖6 h2不同時h1/h3值對CDFSCBS 1階頻率的影響

h1+h3為定值時，在h1/h3=1處出現1階頻率的極小值點和1階損耗因子極大值點，改變阻尼層厚度h2的值，極值點位置不變。這是因為當阻尼層處于中性層位置時，CDFSCBS在純彎曲情況下，中性層受到的剪切應力最大，阻尼層可以獲得較大的應變，由模態應變能原理可知，此時CDFSCBS具有最大的1階損耗因子與相對最小的1階頻率。

當CDFSCBS的上下復合材料層相等時(h1/h3=1)，保持其他材料參數不變，增加阻尼層厚度，CDFSCBS的1階頻率降低，1階模態損耗因子則有較大增加(見圖6與圖7)；當CDFSCBS上下復合材料層不相等時(h1/h3≠1)，增加阻尼層厚度，CDFSCBS的1階頻率與1階模態損耗因子都呈增加趨勢，但變化幅度不大。這是因為隨著阻尼層厚度增加，CDFSCBS的整體阻尼性能得到了提升。又因阻尼層在CDFSCBS中的位置不同，增加其厚度對阻尼性能的提升效果也存在差異，因此阻尼層位于中性層位置更有助于提升CDFSCBS整體的動力學性能。

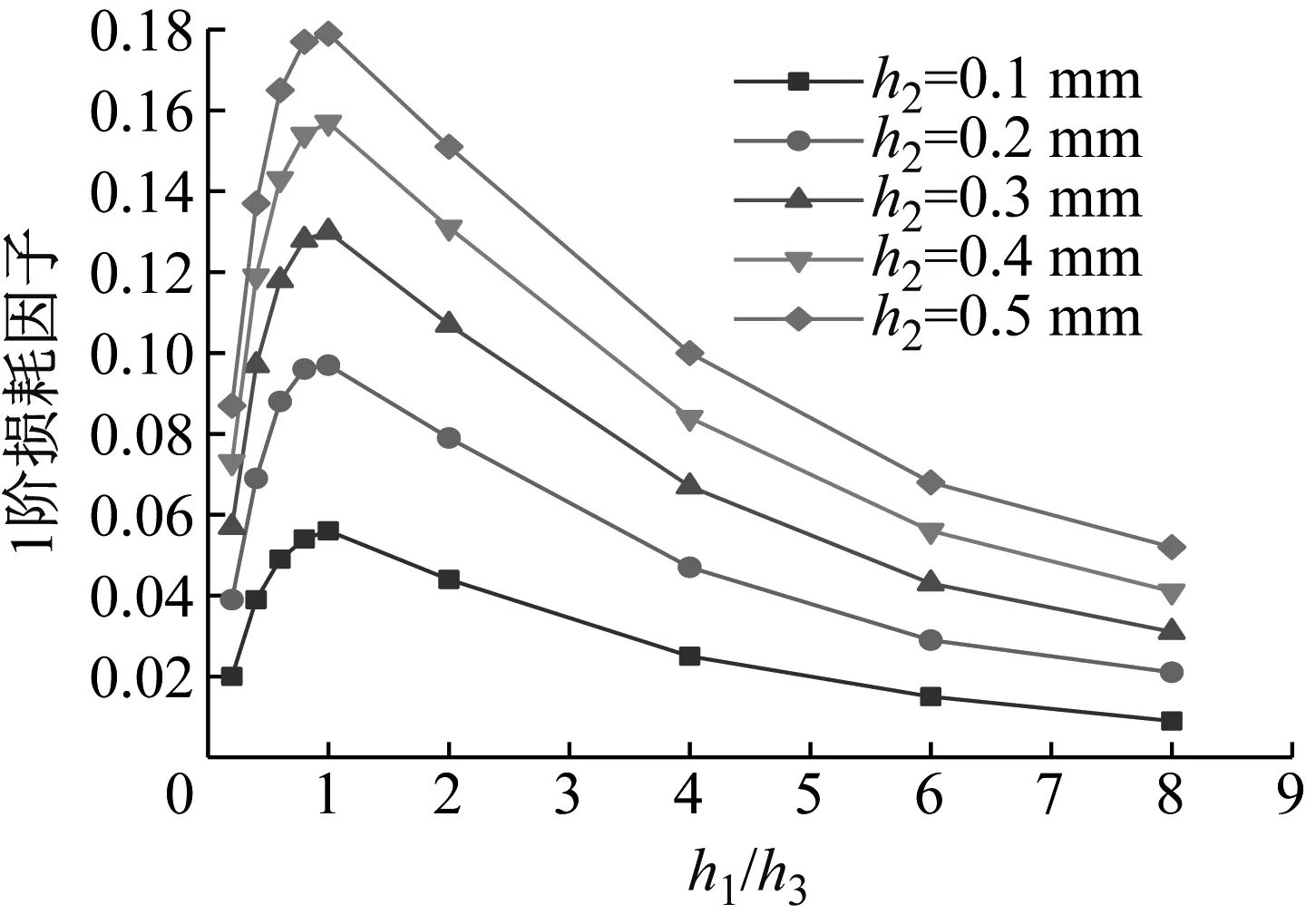
圖7 h2不同時h1/h3值對CDFSCBS 1階損耗因子的影響

3.2 結構幾何參數對動力學性能的影響

增加CDFSCBS的阻尼層厚度可提升其阻尼性能，因此基于阻尼薄膜梁在總厚度不變的情況下，探討黏彈性阻尼層厚度與總厚度的比(Hc/H)和梁長度與總厚度的比(a/H)對CDFSCBS動力學性能的綜合影響規律，結果如圖8～圖23所示。

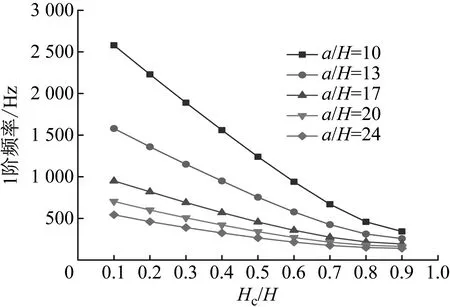
圖8 Hc/H與a/H對CDFSCBS 1階頻率的影響

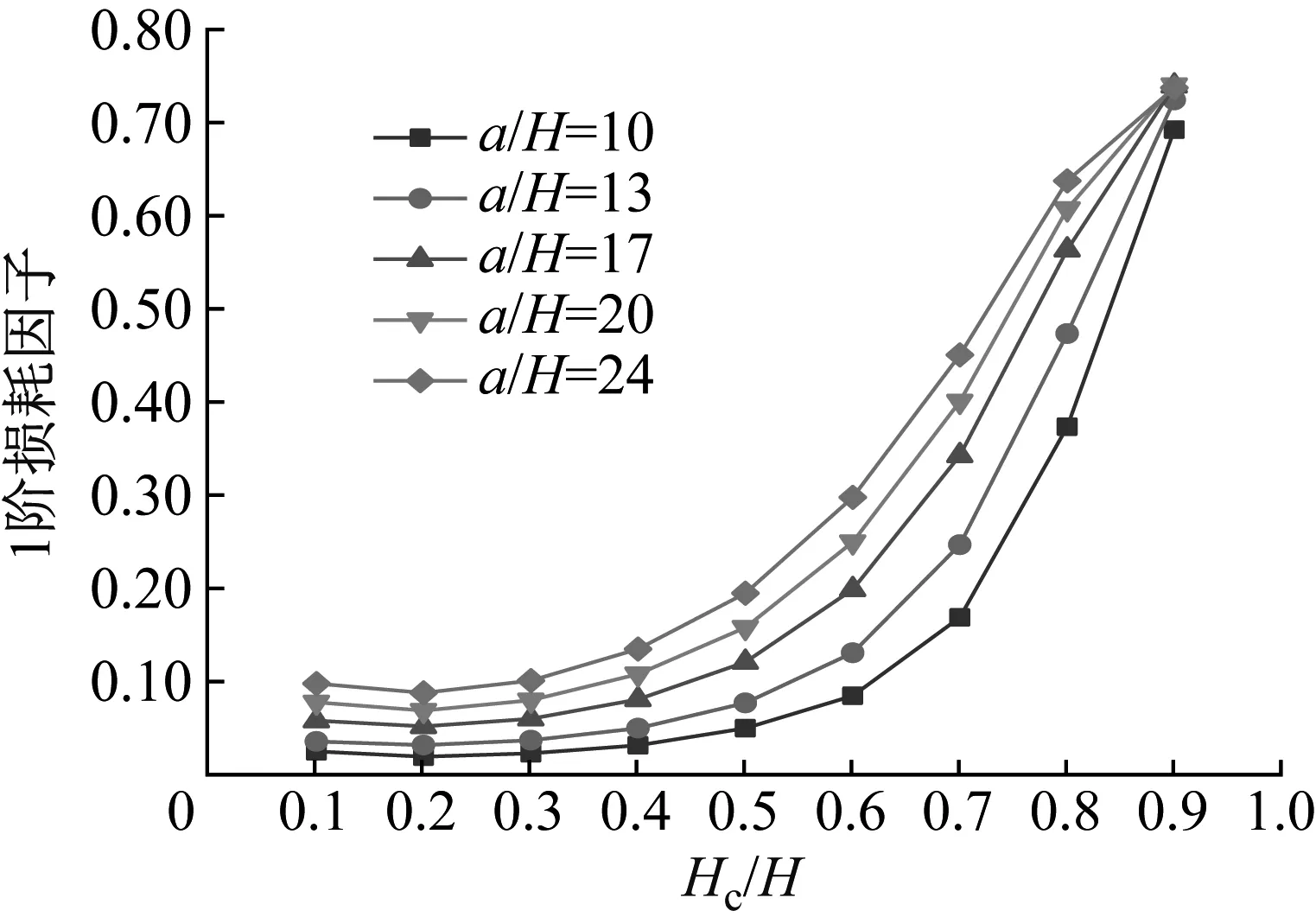
圖9 Hc/H與a/H對CDFSCBS 1階損耗因子的影響

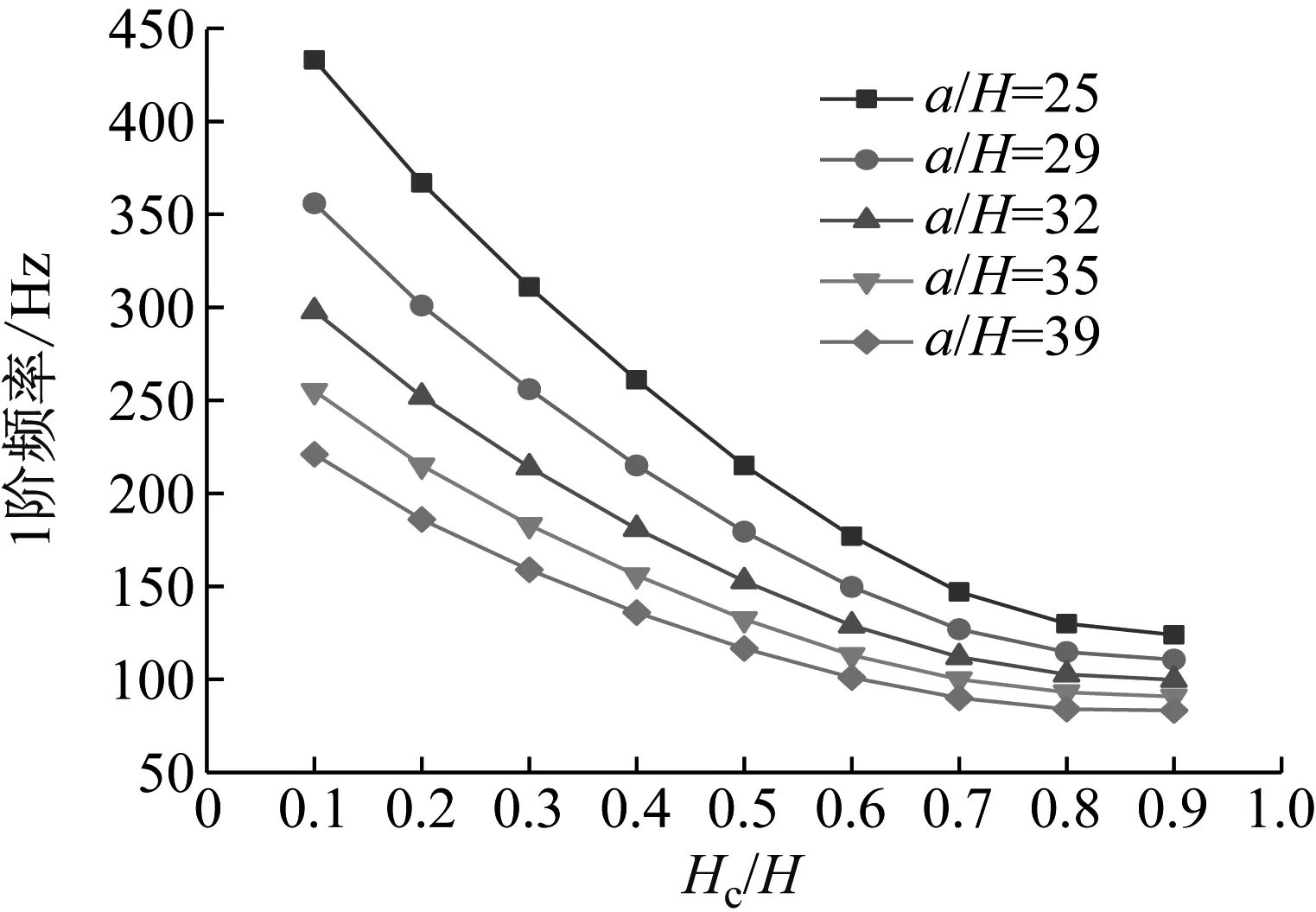
圖10 Hc/H與a/H對CDFSCBS 1階頻率的影響

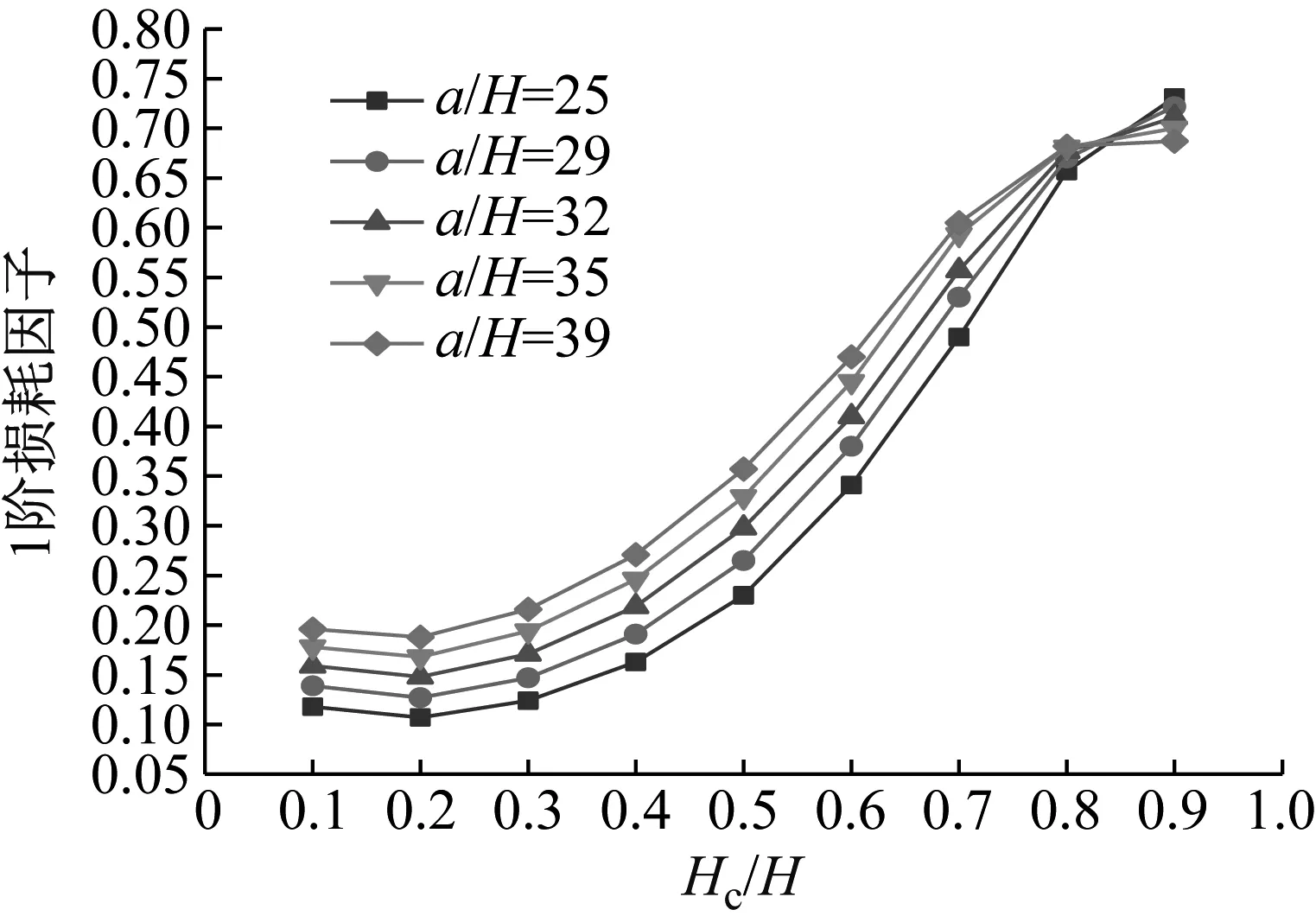
圖11 Hc/H與a/H對CDFSCBS 1階損耗因子的影響

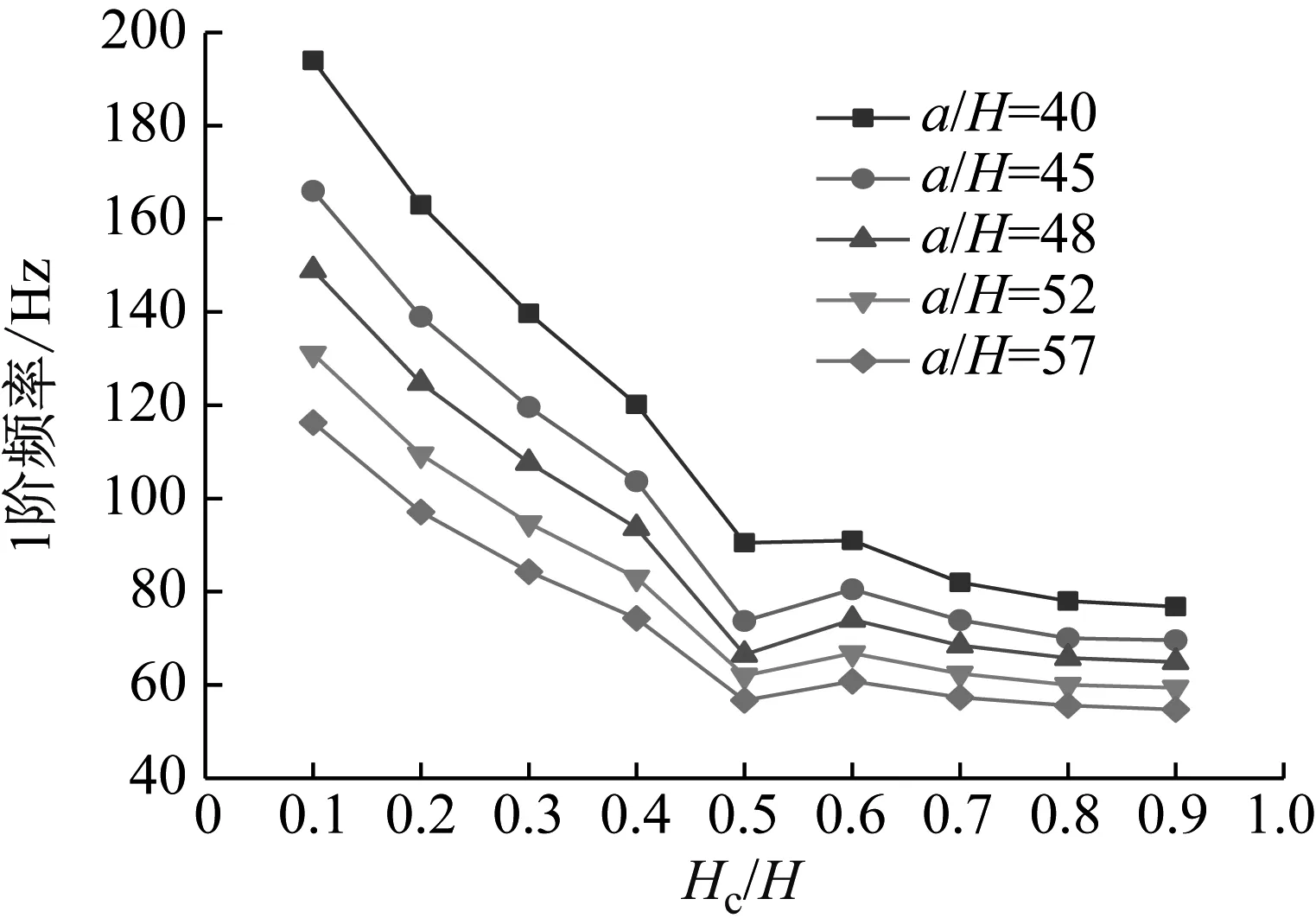
圖12 Hc/H與a/H對CDFSCBS 1階頻率的影響

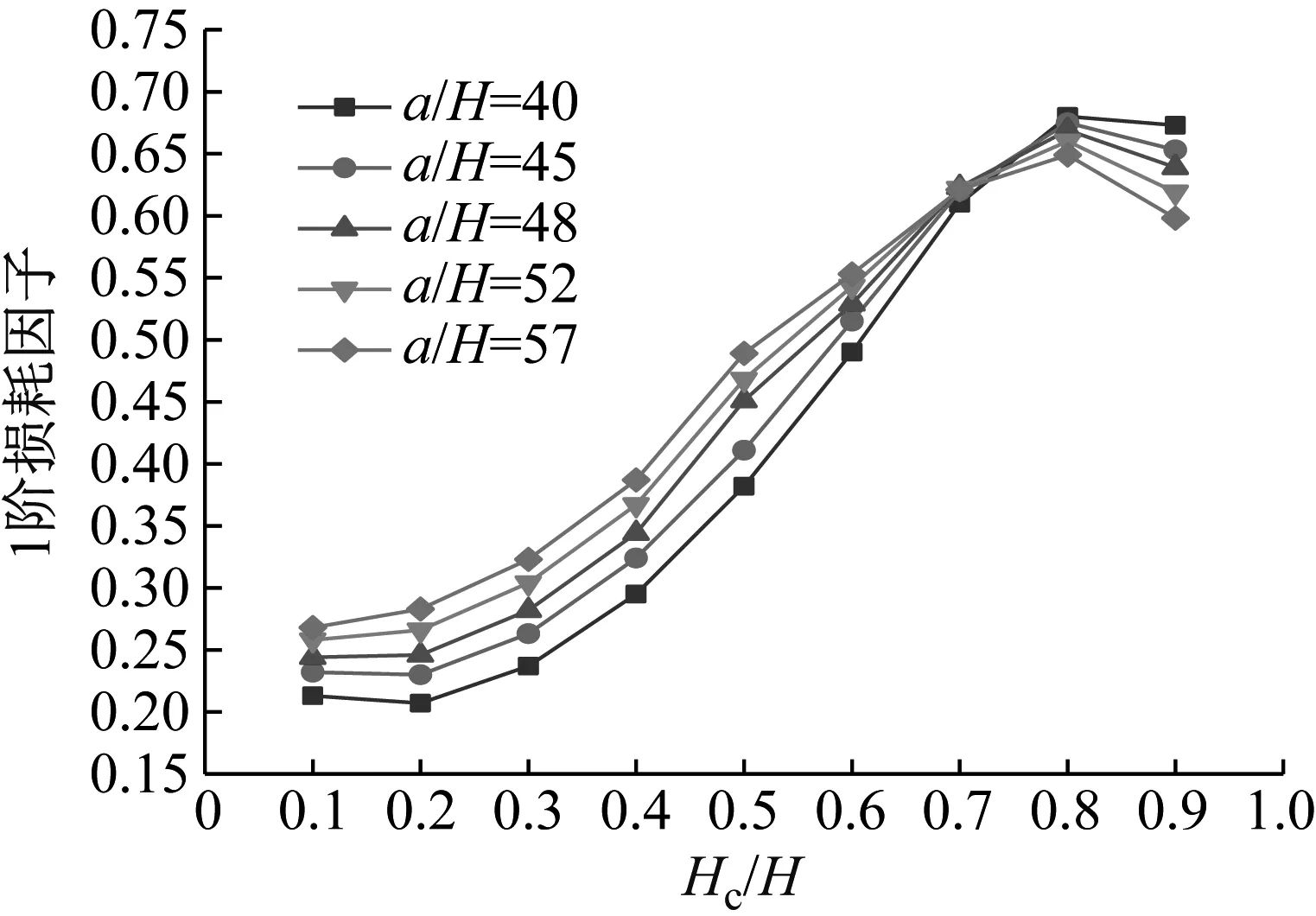
圖13 Hc/H與a/H對CDFSCBS 1階損耗因子的影響

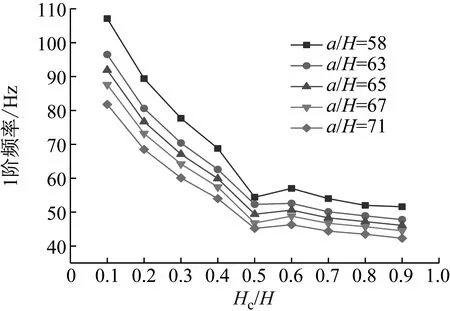
圖14 Hc/H與a/H對CDFSCBS 1階頻率的影響

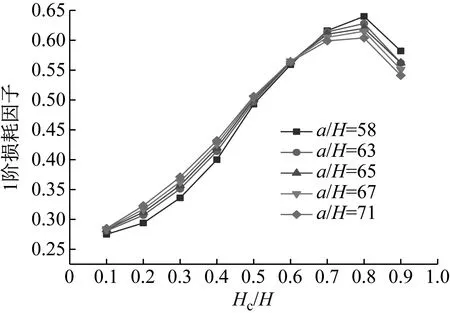
圖15 Hc/H與a/H對CDFSCBS 1階損耗因子的影響

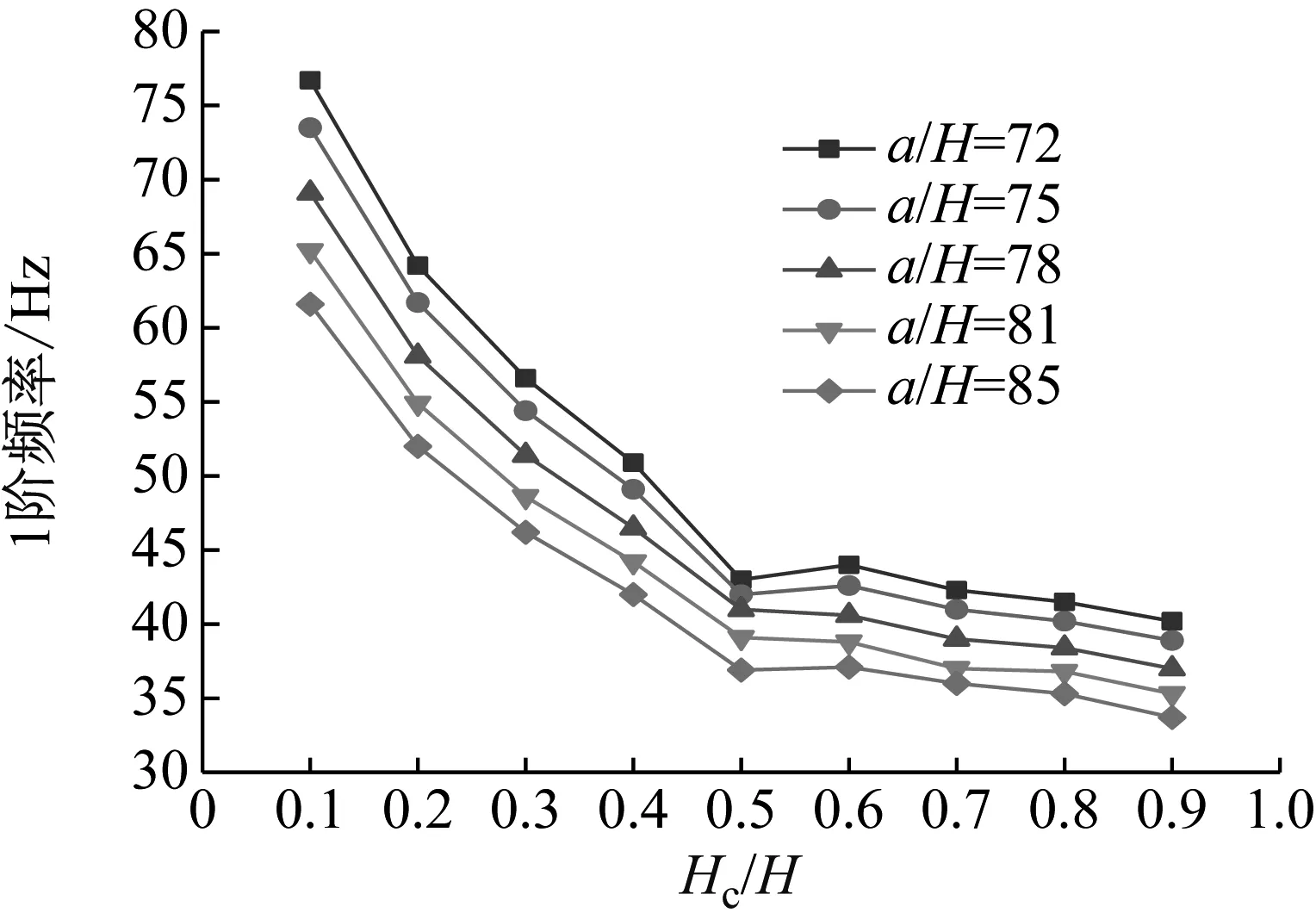
圖16 Hc/H與a/H對CDFSCBS 1階頻率的影響

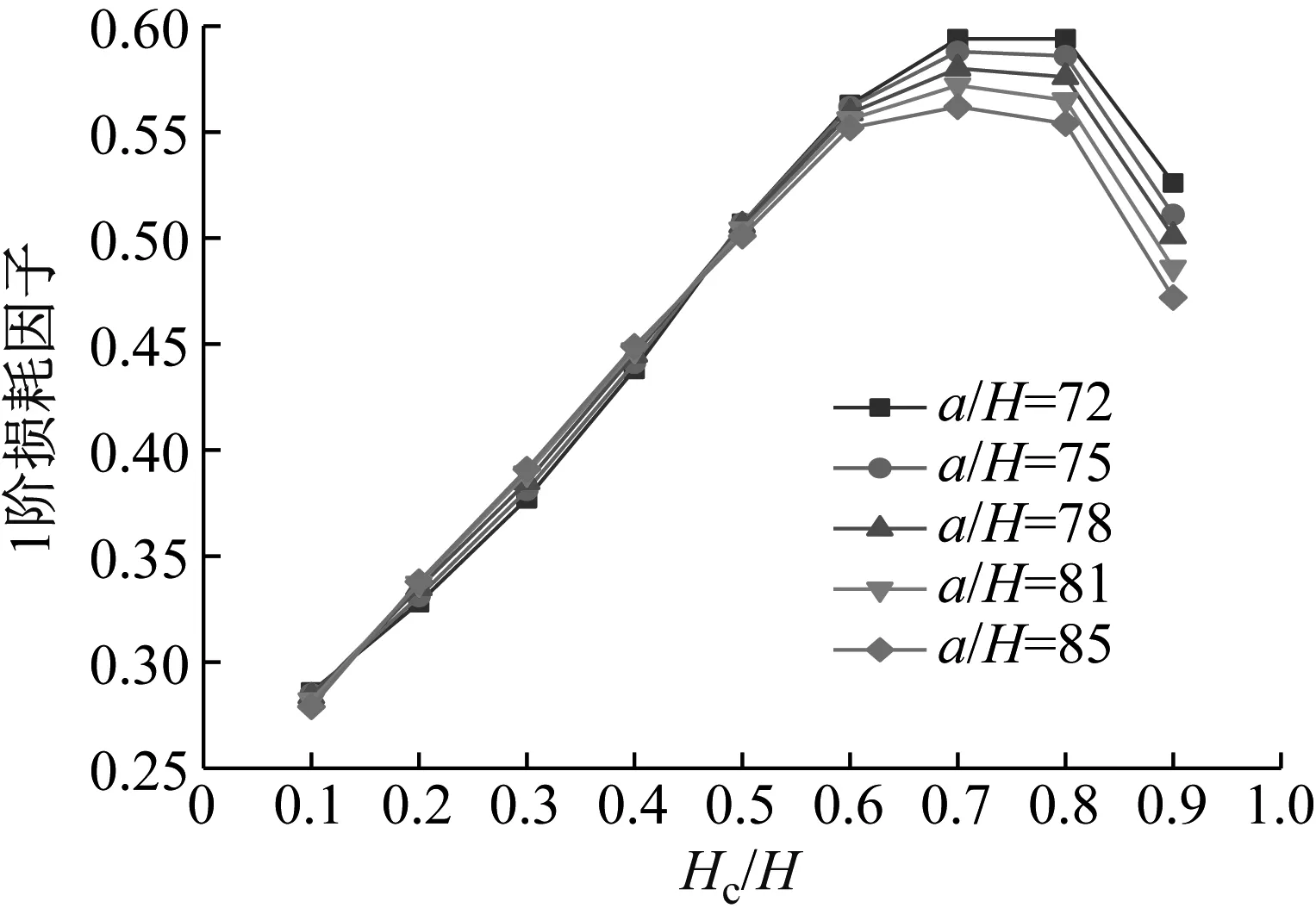
圖17 Hc/H與a/H對CDFSCBS 1階損耗因子的影響

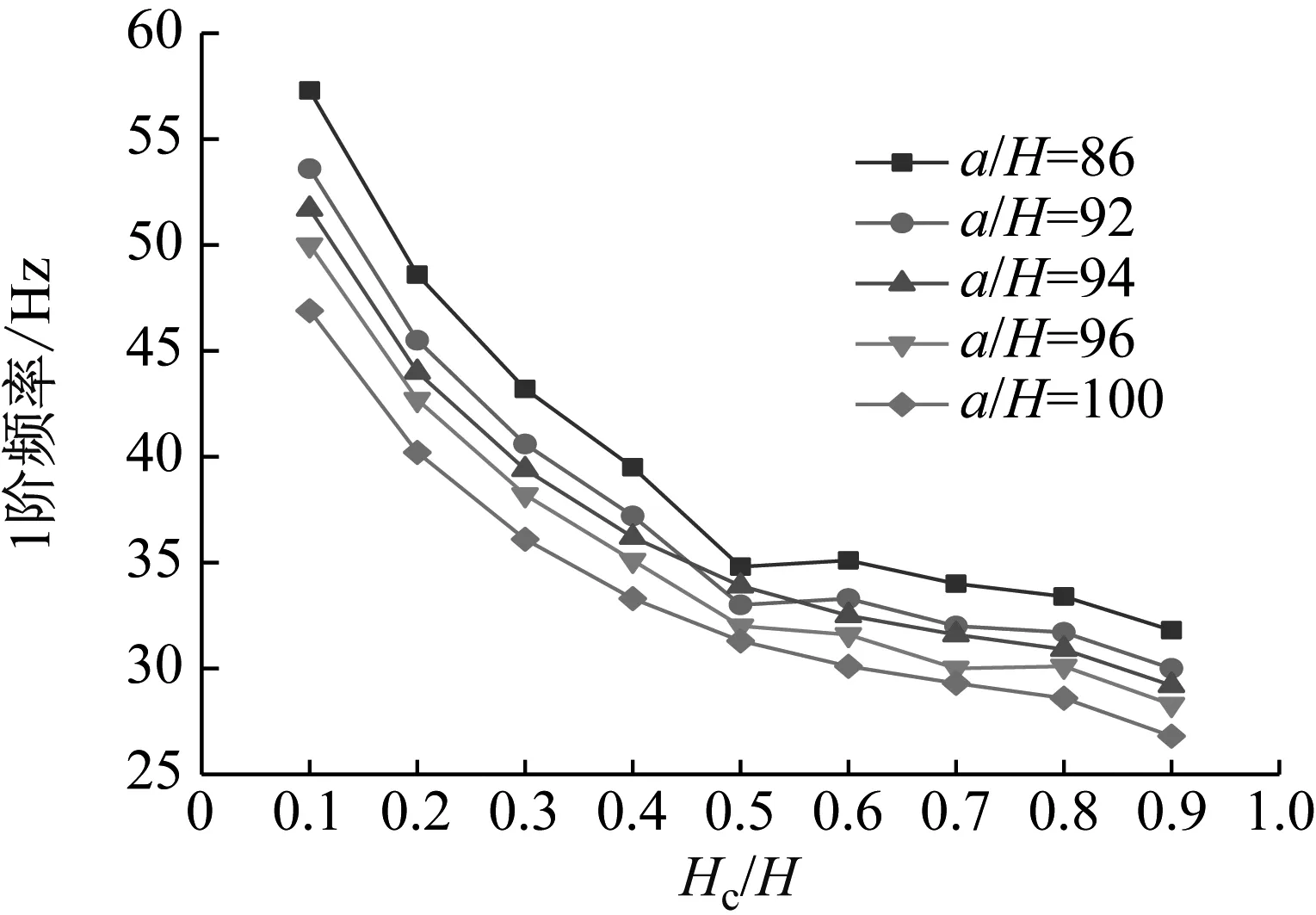
圖18 Hc/H與a/H對CDFSCBS 1階頻率的影響

圖19 Hc/H與a/H對CDFSCBS 1階損耗因子的影響

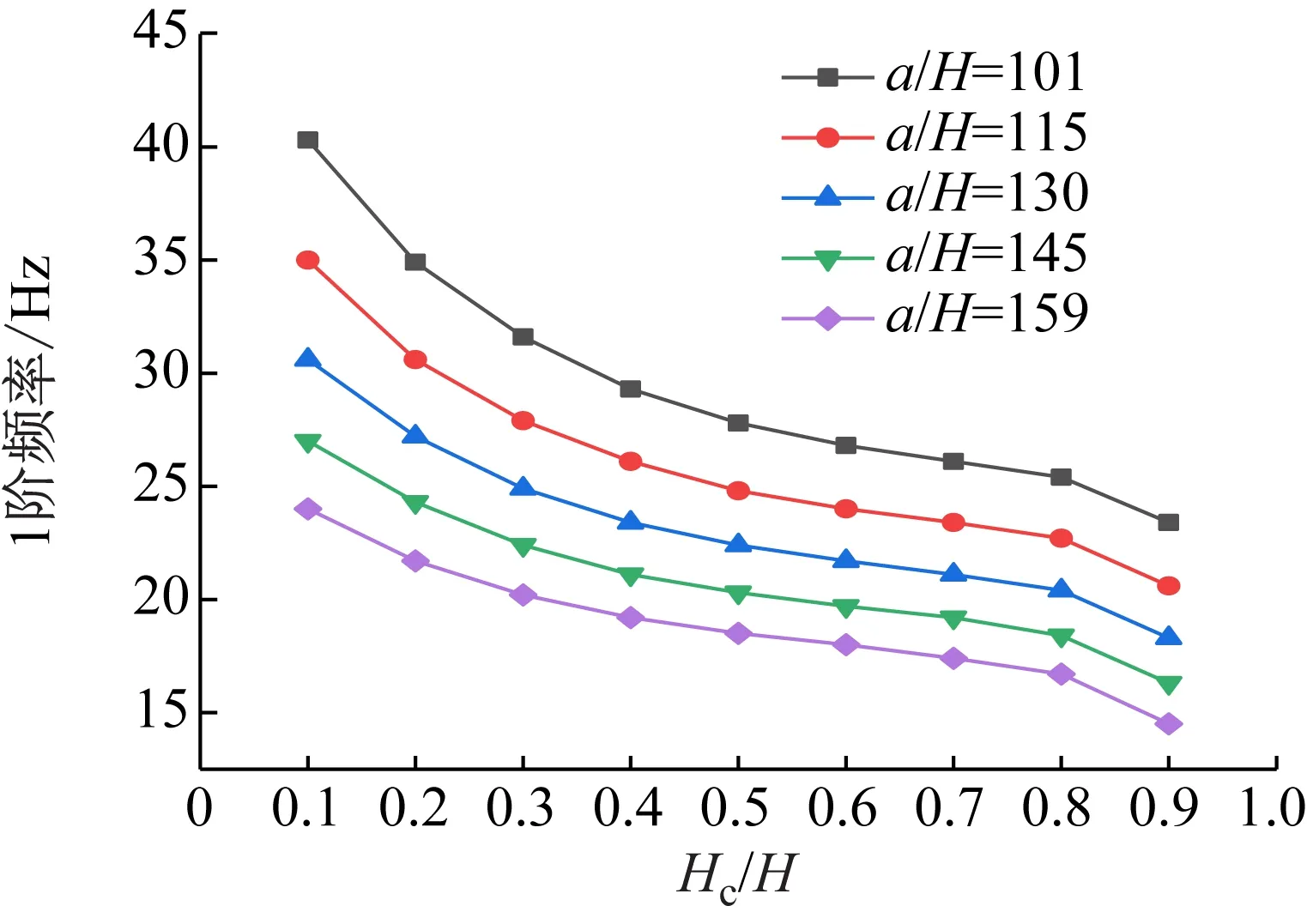
圖20 Hc/H與a/H對CDFSCBS 1階頻率的影響

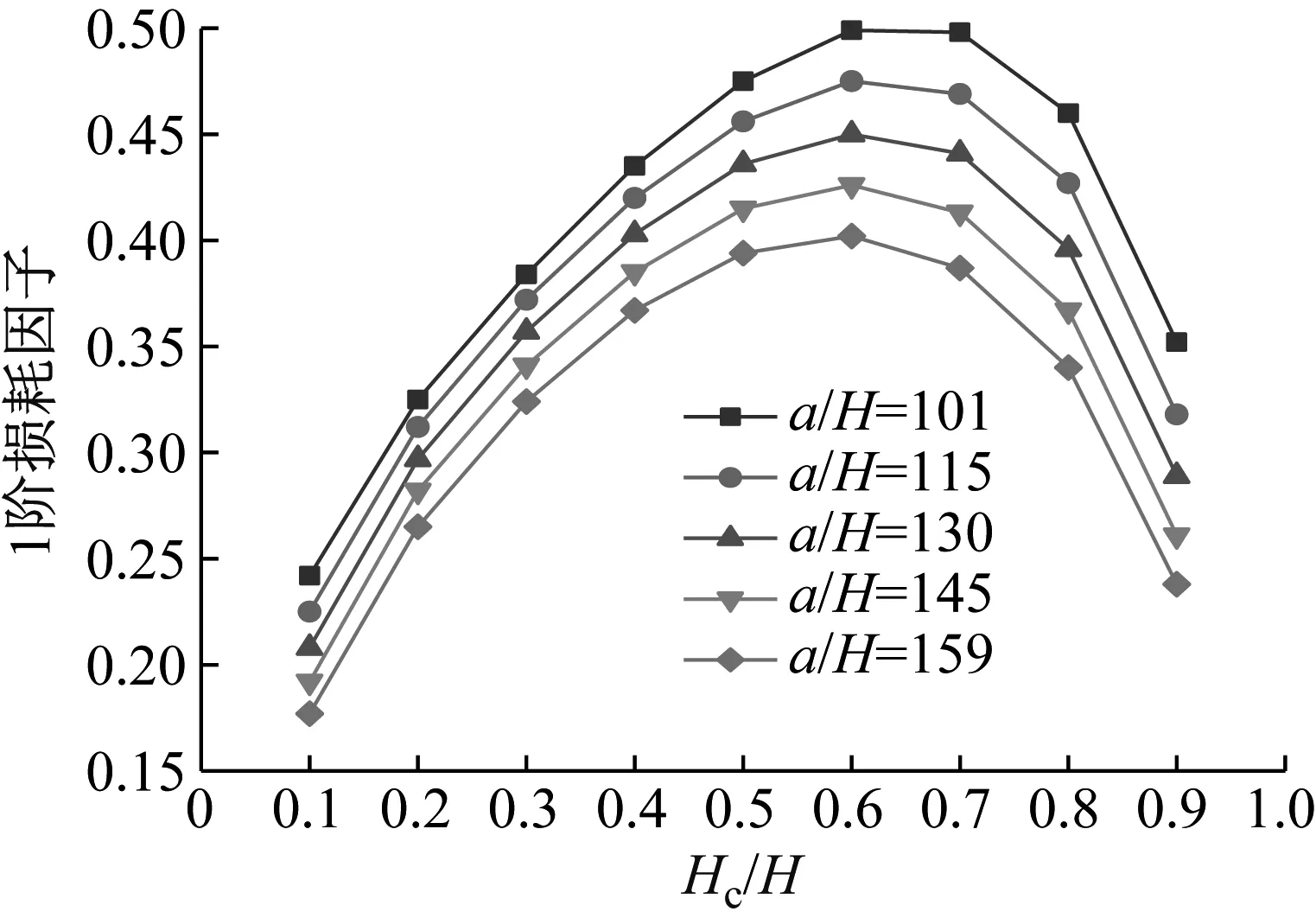
圖21 Hc/H與a/H對CDFSCBS 1階損耗因子的影響

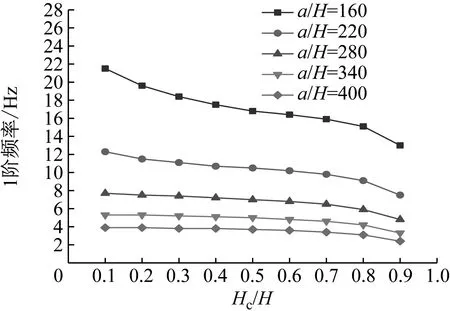
圖22 Hc/H與a/H對CDFSCBS 1階頻率的影響

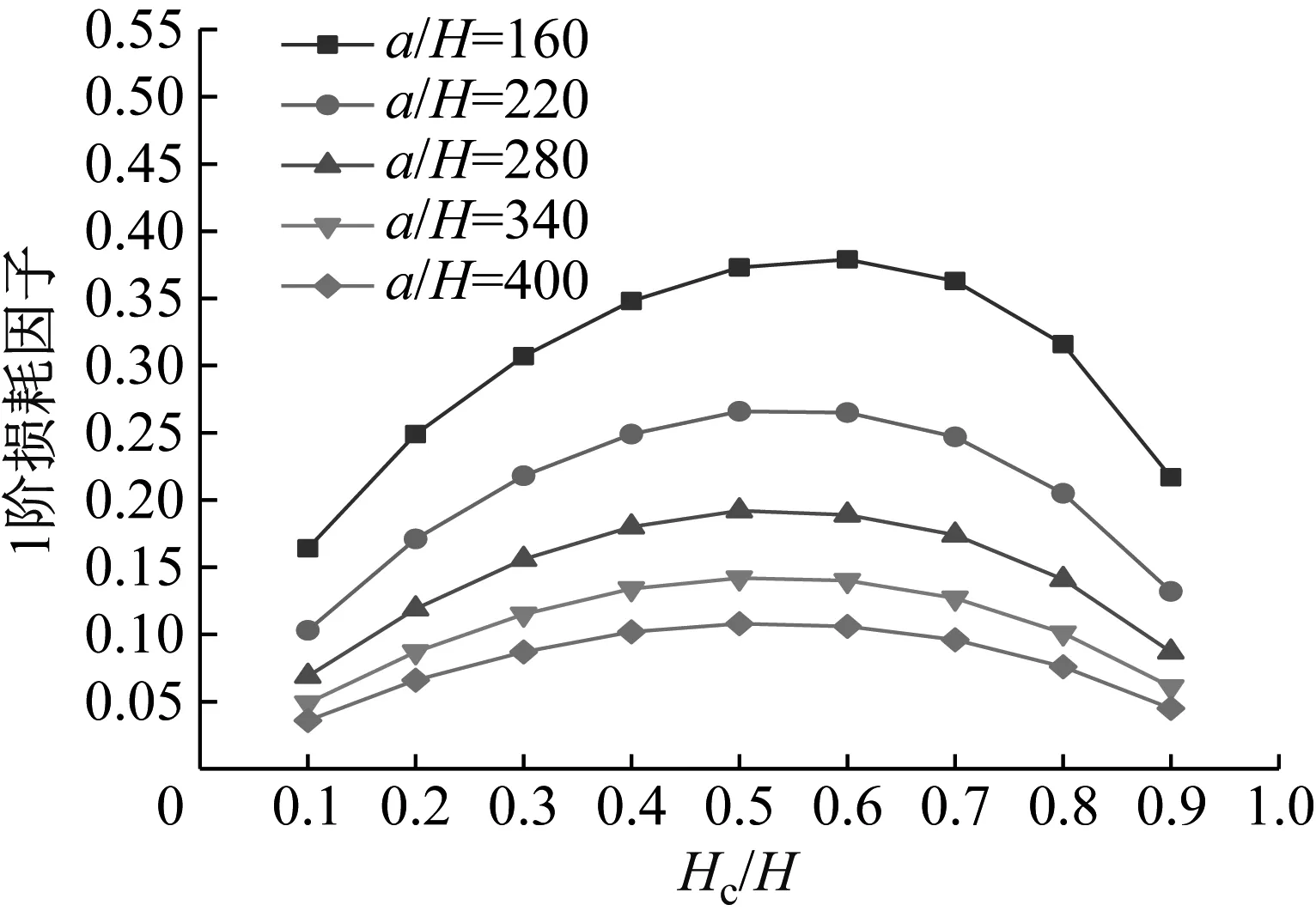
圖23 Hc/H與a/H對CDFSCBS 1階損耗因子的影響

由圖8～圖11可知，隨著a/H與Hc/H值的增加，CDFSCBS的1階頻率呈下降趨勢；1階模態損耗因子整體呈上升趨勢，這是因為a/H在10～39內，隨著Hc/H值的增加，CDFSCBS的阻尼性能一直在提升。因此當a/H在10～39內，CDFSCBS的損耗因子達到最大值時所對應的Hc/H值約為0.9，此時CDFSCBS擁有更好的動力學性能。

由圖12～圖23可知隨著a/H與Hc/H值的增加，CDFSCBS 1階頻率的變化趨勢與圖8～圖11類似呈逐漸下降趨勢，1階模態損耗因子則呈先上升后下降趨勢。在總厚度不變情況下，長厚比不同，損耗因子達到最大值、結構獲得最佳動力學性能所對應的Hc/H值也各有不同。即a/H值約為40～71，對應的Hc/H值約為0.8；a/H值約為72～100，對應的Hc/H值約為0.7；a/H值約為101～159，對應的Hc/H值約為0.6；當a/H值大于160時，對應的Hc/H值約為0.5。

4 結 論

本文基于Hamilton原理與1階剪切變形理論，推導了CDFSCBS的自由振動理論模型，利用伽遼金法求解了模型的理論解。在驗證了理論模型有效性的基礎上，進一步探討了CDFSCBS結構材料分布、幾何參數對CDFSCBS的動力學性能的影響規律。主要結論如下：

(1)當阻尼層位于結構的中性層位置，上下復合材料層關于其對稱分布時，CDFSCBS具有相對最低的1階頻率與最大的模態損耗因子；

(2)通過合理選擇最佳的a/H與Hc/H值，可得到最大的1階模態損耗因子，提升CDFSCBS整體的動力學性能；

(3)分析并得出了Hc/H與a/H之間的最優關系——隨著a/H值的增大，最大損耗因子所對應的Hc/H值約為0.5。