結合拓撲勢與信任度調整的重疊社區發現算法

李曉紅，王閃閃，周學銘，宿 云

（西北師范大學計算機科學與工程學院，蘭州 730070）

0 概述

復雜網絡是指具有自組織、自相似、吸引子、小世界、無標度特征中部分或全部性質的網絡，如現實生活中的交通網、社交網、基因調控網等。社區是指具有相同或相似特性的節點構成的集合，同一社區內部節點之間鏈接的概率比不同社區間節點的鏈接概率高得多，這反映了復雜網絡中個體行為的局部特征及其相互之間的關聯關系。對于社區發現的研究有助于揭示網絡重要結構和功能信息，在過去的幾十年中，研究人員設計了大量的社區發現算法，但隨著研究的深入發現社區結構還表現出重疊特性，例如社交網絡中有一些節點同時歸屬于不同社區，且這種同時屬于多個社區的節點又是信息傳播和網絡演變中的關鍵節點。因此，區分穩定的重疊社區并設計高效的發現算法是亟需解決的問題，受到研究人員的廣泛關注。

目前，重疊社區發現算法主要包括基于派系過濾、基于局部擴張及優化、基于線圖或邊社區3 類。基于派系過濾的重疊社區發現算法［1-2］是一種基于網絡拓撲結構的社區發現算法，從網絡特性出發，認為社區由多個K 派系組成，每個派系都是一個全連通網絡，網絡中的每一個節點可以劃分到不同的K派系中。EVANS［3］提出的Clique Graph 借鑒了派系過濾的思想，通過在網絡中建立派系圖來研究社區結構。盧志剛等［4］提出一種基于貪婪派系擴張（Greedy Factional Expansion，GFE）的重疊社區發現算法。該算法根據企業社會化網絡中極大派系間的鏈接強度將原始網絡圖轉換成最大派系圖，在最大化適應度函數的條件下貪婪擴張最大派系圖中的種子派系進行社區發現。但是，基于派系過濾的重疊社區發現算法受限于網絡中缺失完全子圖，自由參數較多，不同參數設定對結果影響較大，并且經常產生較大的時間復雜度。WEN 等［5］提出一種基于最大團的多目標進化算法（MΟEA）檢測重疊社區。該算法用原始圖的一組最大團作為節點定義，兩個最大團可共享原始圖的相同節點。MΟEA 以類似于非重疊社區檢測的方式處理重疊社區檢測問題。基于局部擴張及優化的重疊社區發現算法通常將種子節點作為初始社區，通過不斷優化質量函數擴展社區，最終得出社區劃分結果［6-7］。代表算法為局部擴展算法（Local Fitness Method，LFM）［8］，LFM 隨機選取一個節點進行擴展，通過迭代局部社區得到重疊社區。CHANG 等［9］提出一種新的重疊社區發現算法ENFI，該算法利用網絡的微觀特征，通過計算朋友親密度提取本地社區并形成網絡的重疊社區。WILDER 等［10］用隨機游走算法為每個節點找出一個子圖，同時計算出該節點的權重以及正比于權重的概率，并以此判定初始節點，該算法的時間復雜度較高。但是以上算法具有不確定性和向外擴展性，形成的網絡模塊容易存在不穩定性和漂移性。基于線圖或邊社區的重疊社區發現算法計算過程復雜，不適用于小規模邊社區。AHN 等［11］根據鏈接網絡非重疊與重疊的轉化思想，對網絡中的鏈接進行層次聚類提出LINK 算法，該算法揭示了這種邊社區在真實網絡中的普遍存在性。除了以上3 類重疊社區發現算法之外，研究人員還提出了一些其他的改進算法［12-14］，均取得了不錯的效果。

本文借鑒物理學勢能中的拓撲勢思想，提出一種基于拓撲勢與信任度調整的重疊社區發現算法。由于網絡中的每個節點周圍存在一個作用場，場中的任何節點都將受到其他節點的聯合作用，因此利用拓撲勢選取核心節點，然后從核心節點出發構建初始社區群，并且充分利用社區間的共享邊越多社區越相容、節點間頻繁的交互和聯系促使社區發生融合這兩個特性，通過調整信任度進行社區合并與調整。

1 相關工作

假設復雜網絡表示為有向圖G=（V，Ε，A），其中：頂點集合V=｛ν1，ν2，…，νi，…，νn｝，n表示節點數；Ai=｛ai1，ai2，…，aim｝表示節點νi的屬性集合，m=|A|表示網絡屬性數。

1.1 改進的節點拓撲勢

在物理學中，場表示物體間的相互作用，這種相互作用并不是接觸才有的，勢表示特定場中的質點從一點移動到另一點時產生的功。勢和場的分布對應物質粒子之間由位置確定的勢能分布［15-16］，并且這種勢能分布與粒子之間的距離成遞減關系，隨著距離的增長勢能下降，直至衰減為0。類比于勢場，網絡中的每個節點周圍存在著一個作用場，位于場中的任何節點都將受到其他節點的聯合作用。通過路徑描述節點之間的聯系，利用路徑長度描述節點間相互作用力的強弱。因此，節點間的相互作用與節點屬性及節點間的距離密切相關，并且每個節點的影響力會隨著節點間路徑長度的增長而衰減。采用高斯勢函數描述這種相互作用，將復雜網絡中節點νi的拓撲勢定義為某個范圍內其他節點在該節點處產生能量的累加和，如式（1）所示：

其中：Γ（νi）表示節點νi影響某個范圍內的節點集合；常數σ∈（0，+∞）用來控制節點的作用范圍；d（νi，νj）表示節點νj到節點νi的最短路徑長度（i≠j）。

首先，為了突出各個節點固有屬性的差異，m（νj）的值由節點屬性值決定［17］。假定節點νi的屬性值為｛wi1，wi2，…，wij，…，wim｝，則節點νi的屬性重要性表示為其次，由于節點在網絡中所處的位置及其鏈接關系存在差異，使得各個節點在網絡中具有不同的重要性。為了突出這種差異，引入位置權重wweight(νj)，表示距離核心節點越遠，位置權重越小。wweight(νj)計算公式如下：

同時，假設式（1）的拓撲勢滿足規范化條件，則?νi∈V的拓撲勢可重寫為：

1.2 信任值調整

從網絡結構的角度來看，兩個節點νi與νj之間擁有的公共鄰居越多，它們越相似。擴展至社區，同樣地，如果兩個社區共享邊較多，就意味著社區間重疊的部分越多，社區就越相容。用于比較有限集合之間的相似性與差異性的Jaccard 系數［18］可描述這種結構上的重疊程度。除此之外，網絡中的節點不是獨立存在的，它們之間具有不同親疏的交互和聯系。社區間的信任解析為彼此所含節點之間的認同，而這種認同實質上是一個互動問題，互動會改變它們之間的關系，使它們發生交叉甚至融合，因此，采用節點間相似度來體現這種互動。綜上，本文基于社區間的共享邊越多社區越相容及節點間頻繁的交互和聯系會促使社區發生融合這兩個特性判斷兩個社區能否合并，稱此過程為調整信任度。調整信任度的計算公式如下：

其中：λ為調節參數（0＜λ＜1），用于控制分析社區間共享邊數和社區間信任度的占比；NNE(Ci,Cj)表示兩社區共享的邊數；T(Ci,Cj)表示社區Ci與Cj的信任度［19］，為兩社區內所有節點間信任度的和。NNE(Ci,Cj)和T(Ci,Cj)的計算公式如下：

其中：N（νi）為節點νi依附的邊構成的集合；N（Ci，Cj）表示社區Ci與Cj合并后所包含的邊。

節點間的信任度采用基于節點屬性的相似度來度量，計算公式如下：

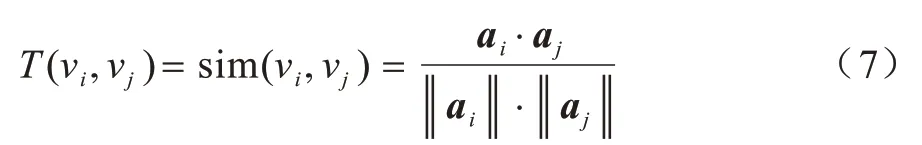
其中：ai、aj分別為節點νi、νj的屬性向量。

2 重疊社區發現算法

本文提出的基于節點拓撲勢和信任值調整的重疊社區發現算法本質上是發現核心節點并以該核心節點為中心進行擴展形成社區的過程。為方便描述，將本文算法簡稱為CTPT 算法。CTPT 算法流程如圖1 所示，其中q表示最終合并社區的個數。

圖1 CTPT 算法流程Fig.1 Procedure of CTPT algorithm

2.1 核心節點選取

首先，計算網絡G中任意一對節點νi和νj的最短路徑長度d（νi，νj），構建最短路徑矩陣MMinDist。然后，利用MMinDist提供的路徑信息，生成每個節點νi的作用節點集合Γ（νi）。接下來，按照式（3）迭代地計算每個節點的拓撲勢φ（νi），并以此為判斷依據選取K個φ（νi）最大的節點作為核心節點，保存在Top 數組中。核心節點選取流程如圖2 所示。

圖2 核心節點選取流程Fig.2 Procedure of core node selection

2.2 社區形成與再調整

在初始化時，將Top［K］中的每一個核心節點視為一個社區。首先，從單節點社區出發，依次取出V中的節點νi并嘗試加入社區IICk，計算模塊度函數Q［20］。如果Q增大，則將該節點加入社區，否則嘗試將節點νi加入下一個社區IICk+1，其中emm表示社區m內部所有節點之間的邊的集合，am表示所有連接到社區m的邊數，emn表示社區m和社區n之間的邊數。然后，通過調整信任度對已形成的初始社區群落進行合并與再調整，上述步驟完成后形成最終社區。未加入任何社區的節點被視為離群點，并將其剔除。社區形成與合并流程如圖3 所示。

圖3 社區發現與合并流程Fig.3 Procedure of community discovery and merging

3 實驗結果與分析

3.1 實驗設置

3.1.1 數據集

為評價CTPT 算法性能，實驗采用兩類數據集：1）LFR 人工網絡數據集，由經典的LFR 基準程序生成，可以模擬具有重疊社區結構的網絡數據集，主要用于測試社區檢測算法的優劣；2）真實網絡數據集，來源于斯坦福大學的大型網絡數據集網站（http：//memetracker.org/data/index.html）。表1 給出了人工網絡數據集Net1、Net2 和Net3 的參數信息，其中，Οn表示重疊節點數，μ表示LFR 網絡中的混合系數，其值越大表明所生成的網絡拓撲結構越復雜。表2 給出了真實網絡數據集ego-Facebook、Musae-twitch 和Web-flickr 的參數信息。ego-Facebook 數據集由facebook 的朋友列表組成，是facebook 上用戶間的社交網絡。Musae-twitch 數據集是使用某種語言進行流式傳輸的游戲玩家的Twitch 用戶-用戶網絡，該網絡中的節點是用戶本身，鏈接是他們之間的好友關系。Web-flickr 是用戶分享圖片和視頻的社交網絡，該網絡中每一個節點都是flickr 中的用戶，每一條邊都是用戶之間的好友關系。另外，每一個節點都有標簽，用于標識用戶的興趣小組。

表1 LFR 人工網絡數據集參數設置Table 1 Parameter setting of LFR artificial network dataset

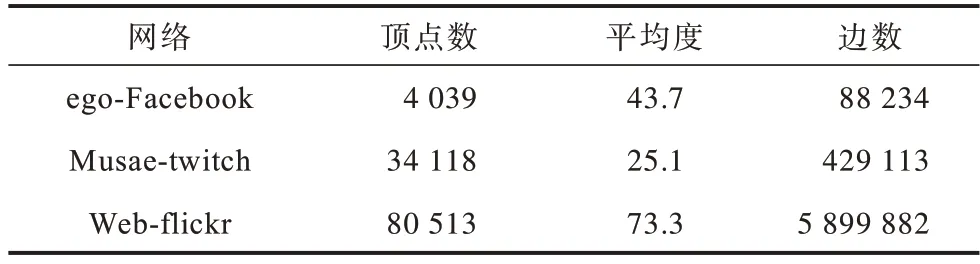
表2 真實網絡數據集參數設置Table 2 Parameter setting of real network dataset

為評價算法性能，通常需要選取度量社區劃分好壞的性能指標。擴展模塊度是最常用的指標之一，計算公式如下：

指標歸一化互信息（Normalized Mutual Information，NMI）［21］用于度量檢測到的社區與真值之間的距離，計算公式如下：

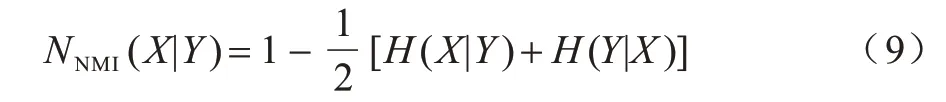
其中：H（X|Y）表示X對Y的規范條件熵；H（Y|X）表示Y對X的規范條件熵，該值越大，意味著算法所發現社區與網絡真實社區相吻合的程度越高。

3.1.2 對比算法

將本文提出的CTPT算法與以下4種算法進行對比：

1）基于隸屬度傳播（Membership-Degree Propagation，MDP）的重疊社區劃分算法［22］：以種子節點的基本特征為依據構建網絡節點之間的隸屬度傳播模型，將種子節點的社團隸屬度傳播至非種子節點進行社區發現。

2）面向屬性網絡的重疊社區劃分算法（overlapping community discovery Algorithm for Attributed Networks，ANA）［23］：利用節點的密集度和間隔度搜索局部密度中心，并將其作為社區中心，通過計算非中心節點的社區隸屬度實現重疊社區的劃分。

3）基于GFE 的重疊社區劃分算法［4］：根據網絡中極大派系間的鏈接強度將原始網絡圖轉換成最大派系圖，在最大化適應度函數的條件下，貪婪擴張最大派系圖中的種子派系進行社區發現。

4）基于種子擴張（Two Expansions of Seeds，TES）的重疊社區劃分算法［24］：首先根據網絡節點的拓撲特征形成初始社區，然后采用重力度再次進行社區的合并和擴展。

3.2 結果分析

3.2.1 LFR 人工生成網絡數據集上的結果分析

圖4 給出了在不同規模的LFR 人工生成網絡數據集上5 種重疊社區發現算法隨重疊社區數量變化對應NMI 的變化規律。CTPT 算法考慮不同結構和屬性的影響，分別設置調整信任度的調節參數λ為0.4、0.5、0.6，實驗結果顯示λ=0.5 時效果最好。

圖4 不同重疊社區數量對算法NMI 值的影響Fig.4 Influence of the number of different overlapping communities on the NMI value of the algorithm

通過觀察圖4 中NMI 變化曲線可以發現：隨著重疊社區數量的增加，5 種算法在3 組數據集上的NMI 值不斷減小；隨著網絡規模的增大，5 種算法的效率均有所下降，但CTPT 算法的社區劃分效果相對較好，并且具有較好的穩定性。其中，ANA 算法在Net3 網絡數據集上表現較差，NMI 值下降較快，比其他算法效率差。同時，對比CTPT 算法在3 個網絡數據集上的效果后發現，CTPT 算法在Net3 網絡數據集上得到的NMI 值低于Net1 和Net2 網絡數據集，意味著網絡越復雜，CTPT 算法的執行效果越差，這是下一步需要改進之處。由此可見，在大規模復雜網絡數據集的重疊社區檢測方面，CTPT 算法具有較好的檢測效果和穩定性。

3.2.2 真實網絡數據集上的結果分析

在真實網絡數據集上采用擴展模塊度進行重疊社區發現算法的性能評估。表3、表4 給出了CTPT算法在3 個真實網絡數據集上實驗結果，分別選取社區數量|C|在不同值的情況下，運行15 次CTPT 算法所得的EQ 均值作為最終結果。

表3 真實網絡數據集上社區發現的EQ 值（|C|=20）Table 3 EQ value of community discovery on real network dataset（|C|=20）

表4 真實網絡數據集上社區發現的EQ 值（|C|=30）Table 4 EQ value of community discovery on real network dataset（|C|=30）

由于CTPT 算法充分考慮了社區形成過程中各種因素的共同作用，一方面引入拓撲勢，考慮了網絡結構（最短路徑長度）不同導致的節點重要性不同，另一方面多次融合節點屬性，兼顧了節點交互對社區的影響，因此在真實網絡數據集上性能表現良好，實驗結果整體優于對比算法。TES 算法與CTPT 算法的第一階段均為使用網絡的節點拓撲特征得到初始社區，在3 個網絡上的EQ 值僅次于CTPT 算法，表現較好，尤其是在Musae-twitch 網絡數據集上，在最好情況下EQ 值僅相差0.025。ANA 算法實現時會產生較小的鏈接社區，阻礙了社區的形成，導致難以獲得較好的性能，因此在3 個數據集上的實驗結果均是最差的。

4 結束語

本文充分考慮社區形成過程中各種因素的共同作用，提出基于網絡拓撲勢與信任度調整的重疊社區發現算法。由于節點在網絡中所處位置及其鏈接關系存在差異，使得節點重要性不同，通過網絡拓撲勢來體現這一特征，并且每個節點又具有獨立的固有屬性，因此將屬性的影響力疊加在拓撲勢的計算過程中。在社區合并階段，將節點間的信任度作為初始社區能否合并的依據，形成最終的社區劃分。在不同數據集上的實驗結果驗證了本文算法相對于同類算法的優越性。在下一階段的研究中將嘗試在核心節點的選取中加入注意力機制來體現節點重要性，利用圖嵌入技術優化生成的屬性向量，提升重疊社區發現算法的實現效率，并最終將其應用于實際網絡分析及網絡推薦系統。