雙向二維快速伺服刀架的前饋控制研究

武志士，李國平，鄧益民，趙琪嘯，徐少巖，楊依領(寧波大學 機械工程與力學學院, 浙江 寧波 315211)

0 引言

快速伺服刀架是指伺服控制的快速進給刀架系統[1]，主要用于精密制造。配合快速伺服刀架，可使刀具產生快速而微小行程的高精度進給運動(位置精度可達納米級)。此外，快速伺服刀架還可實時跟蹤設計表面形狀，能在一次加工中獲得高精度表面輪廓及可用于復雜表面形狀的精密加工[2]。基于這些優點，快速伺服刀架技術已成為一種重要的微結構表面加工方法。快刀伺服系統具有的快速性要求其驅動器能產生高頻運動，壓電陶瓷致動器可以滿足這一要求。因此，許多學者提出并實現了由壓電陶瓷致動器驅動快速伺服刀架系統。通過引入柔性鉸鏈作為位移放大機構，快速刀架能實現大位移輸出[3]。引入放大機構使刀架位移輸出有較大的增長[4]，但同時導致了響應頻率降低[5]。壓電陶瓷致動器的另一個特點是正向運動的性能比反向運動的性能好，反向運動時間較長使整體運動時間長。通過對向放置壓電陶瓷致動器能有效地消除反向運動的負面影響，從而減少快速伺服刀架的響應時間。當一個制動器前進同時另一個制動器后退，反向力夾持下比單個制動器驅動時響應快。因此，雙向驅動的快速伺服刀架比單向驅動的快速伺服刀架頻率響應快[6-7]。由于一些復雜輪廓的加工需較復雜的伺服運動，而單自由度快速伺服刀架無法實現。因此，多自由度快速伺服刀架[8-9]已倍受關注。

壓電陶瓷制動器存在遲滯特性，將降低快速伺服刀架的輸出定位精度。為了消除遲滯的影響，需要通過構建遲滯模型建立前饋控制。已有研究中，建模方法主要有Preisach模型[10]、Prandtle- Ishlinskii模型[11]及Maxwell模型等[12- 14]，但由于數學理論發展的局限性，這些模型的準確率已達極限。近年來引入了其他一些滯后模型(如Bouc-Wen模型[15-16]、LuGre模型[17]等)，并取得了較好的效果。與其他遲滯模型相比，Bouc-Wen模型具有計算簡單，易得到逆模型，待求參數少的優點，但其存在參數冗余問題，導致經典Bouc-Wen模型的參數難以識別，阻礙了其應用。通過歸一化處理能保證Bouc-Wen只依賴于一組特定的參數。

本文搭建了基于雙向壓電驅動的二自由度快速伺服刀架的實驗測試平臺，獲得了具有遲滯特性的位移曲線。然后采用基因遺傳算法求解了Bouc- Wen模型的參數，對其進行求逆運算解得逆模型。最后依據逆模型構建了前饋控制環節，對快速伺服刀架進行了不同電壓信號下的運動補償及二自由度運動性能測試。

1 Bouc-Wen模型及其歸一化

1.1 經典Bouc-Wen模型回顧

Preasch、PI、Bouc-Wen和Duhen模型等都對遲滯特性有準確描述。經典Bouc-Wen模型是由Bouc提出，被Wen進一步修改以模擬振動力學的滯后現象。Bouc-Wen模型具有能描述多種遲滯類別的能力和易計算的優點，這使大多數研究人員致力于探索該新興模型的廣泛使用。該模型輸入和輸出間的關系為

y(V,t)=αkV(t)+(1-α)Dkh(t)

(1)

(2)

式中：y(V,t)為滯后輸出位移；V(t)為輸入到快刀伺服刀架的電壓；αkV是模型中彈性項和由參數α、k、D組成的純滯后項(1-α)Dkh;h(t)為遲滯效應的輔助變量，它是非線性一階微分方程(2)關于參數A、β、γ、n(n≥1)的解。通過正確選取這些參數值，可獲得范圍廣泛的遲滯曲線。

1.2 歸一化處理

迄今為止，許多研究工作都聚焦在Bouc-Wen模型的不對稱性上，而經典Bouc-Wen模型中存在的參數冗余問題同樣制約著模型的應用。因此,有必要對Bouc-Wen模型進行歸一化處理,以避免參數冗余問題。為了準確描述普遍的參數冗余問題，現給出兩組不同參數：n1=n2=n,A1=A2,α1=α2,k1=k2,β2=cnβ1,γ2=cnγ1,D2=cD1,其中c為正常數，初始條件h1(0)=h2(0)=0。因此，式(1)、(2)中Bouc-Wen模型可改寫為以下兩種形式：

(3)

及：

(4)

根據給定參數，方程(4)可轉化為

(5)

令ha(t)=ch2(t)，則方程(5)可表示為

(6)

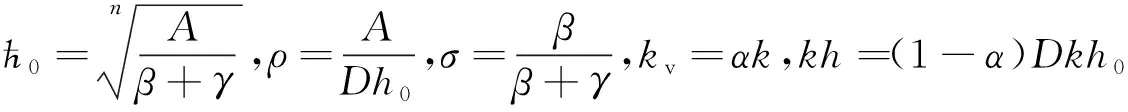
y(V,t)=kvV(t)+kh?(t)

(7)

(8)

圖1為歸一化Bouc-Wen模型在一組特定參數下得到的遲滯曲線。

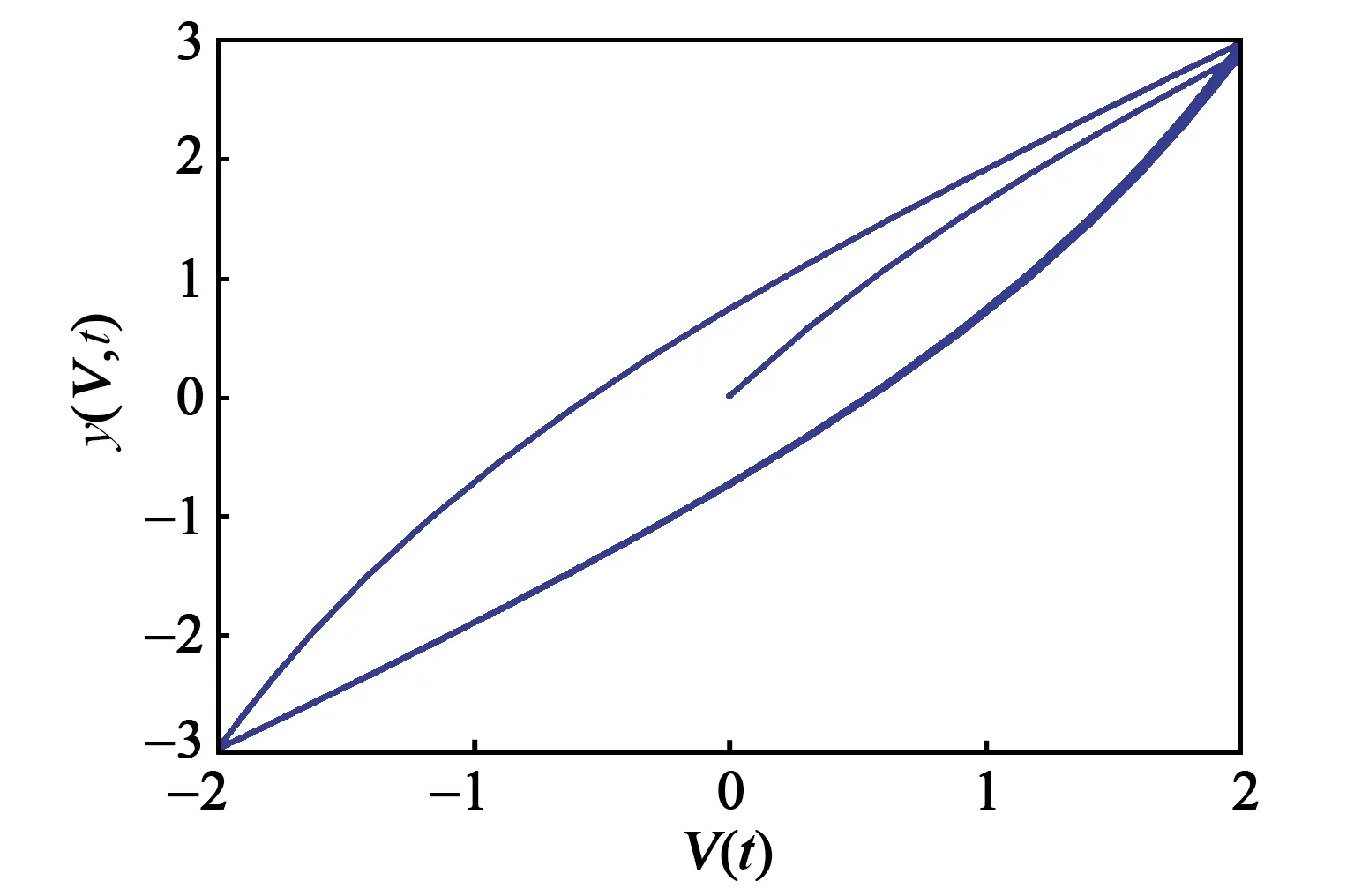
圖1 模型生成遲滯曲線

1.3 模型求逆

除了避免參數冗余問題外，歸一化后Bouc-Wen還具有逆模型易取的特點。根據式(7)、(8)可以求得歸一化后Bouc-Wen模型輸入、輸出間的關系為

(9)

式中：yd(t)為預期位移；Vb為對輸出電壓施加的偏置電壓，從而避免信號電壓中出現負值；h(t)是由非線性微分方程求解得到，代表逆模型中的遲滯環節。kv、kh是模型中待求取的參數，由遺傳算法得到。因此，通過簡單的運算可得補償后的輸入電壓。

2 實驗測試平臺搭建

為了對快速伺服刀架進行任意信號的輸入控制及輸出測量，搭建了實驗平臺。其中4個壓電陶瓷驅動器(直徑?7 mm，長28 mm，自由行程30 μm)用于產生高精度輸入位移。使用兩個光學位移傳感器(Keyence，LK-G80，分辨率為0.15 μm)測量末端執行器的響應。電壓放大器的電壓調節范圍為0～150 V。使用的A/D模塊型號為NI-PCI-6221。整個測試系統基于Labview軟件實現。

3 參數識別

歸一化Bouc-Wen模型中僅含有kv、kh、ρ、σ和n5個未知參數，因而求解工作減少。最小均方根算法、粒子群優化算法和差分進化算法等智能算法常被用以求取Bouc-Wen模型參數。本文使用了在穩定性和收斂速度上均優于傳統遺傳算法的自適應遺傳算法，其流程圖如圖2所示。

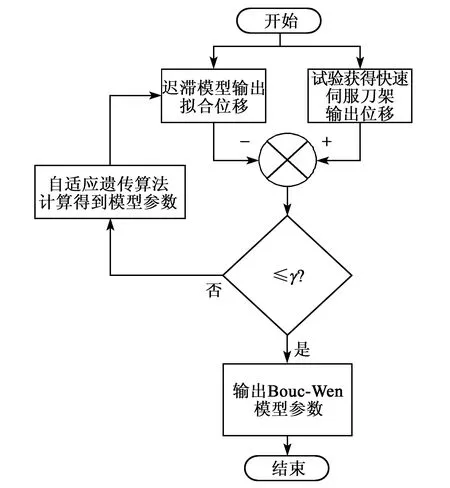
圖2 參數求解流程圖

本文選擇均方根誤差來評判模型與真實值之間的偏差：

(10)

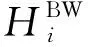
驗證實驗中所使用的輸入為正弦波電壓信號及由實驗所測得快速伺服刀架的位移。雖然在自適應遺傳算法中設置更多的種群數和遺傳代數會提高擬合精度，但增加了時間。因此,本文選擇初始種群為50，遺傳代數為100,求解后結果如表1所示。

表1 Bouc-Wen模型參數表

由表1可看出，正弦波最佳適應度為0.28 μm，這說明歸一化Bouc-Wen模型預測的結果與實驗擬合度較高。

將求得參數代入歸一化后Bouc-Wen模型中，可獲得預測的位移曲線如圖3所示。圖中，實驗曲線是通過施加一個正弦波電壓信號(振幅75 V，頻率1 Hz)到快速伺服刀架測得。

圖3 模型預測曲線(正弦波)圖

由圖3可看出，模型值與實驗值產生的誤差主要位于峰頂處。由圖3中誤差曲線可知，在初始加載過程中實驗與模型出現最大誤差，每個峰值的偏差比其他時間大。這是因為歸一化Bouc-Wen模型存在非線性微分方程，其求解結果為近似值，具有一定偏差，且在每個峰頂處，電壓信號的變化率最大。這些因素一起作用導致了歸一化Bouc-Wen預測曲線在每個峰頂偏差較大。初始部分出現最大偏差的原因是實驗獲取的位移曲線在開始階段表現出較強的非線性，這使模型無法準確預測。

4 補償與驗證

圖4為對快速伺服刀架進行遲滯補償的結構圖。圖中，yd(t) 為期望得到的位移，u(t) 為Bouc-Wen逆模型產生的驅動電壓，y(t) 為得到的驅動電壓u(t)施加到快速伺服刀架后得到的實際位移，FTS為快速伺服刀架。以期望位移作為輸入，輸出為補償電壓，將得到的具有補償效果的電壓信號施加到快速伺服刀架，可得補償后的實驗位移。通過實驗可知，前饋控制下快速伺服刀架能準確地得到期望軌跡。

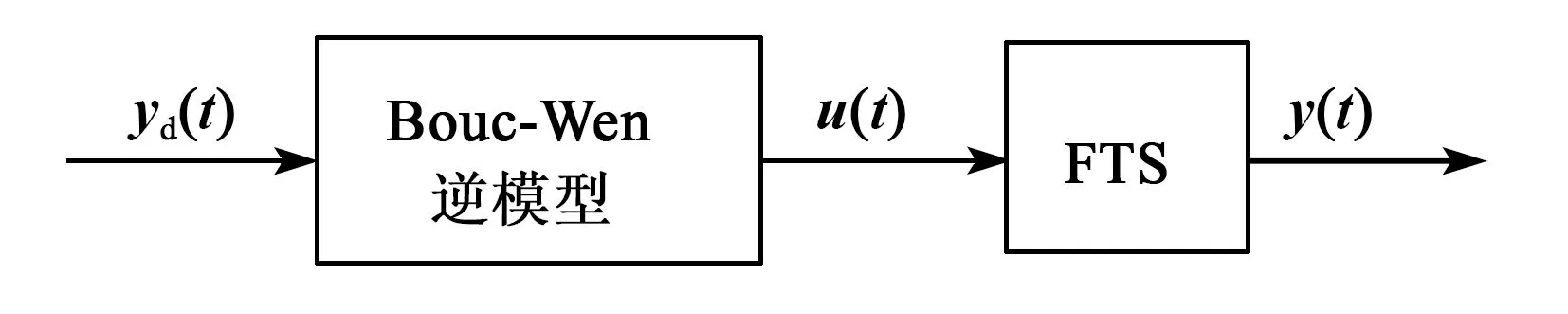
圖4 前饋遲滯補償流程圖

為進一步驗證模型的有效性，采用幅值45 μm、頻率1 Hz的等幅正弦波期望位移信號進行軌跡跟蹤實驗。式(9)得到了補償電壓在每一時刻的數值。因為有偏置電壓Vb的存在，所以理想電壓與補償電壓的起點都不為0，如圖5所示。由圖可看出，在上升階段，補償電壓大于理想電壓；下降階段，補償電壓小于理想電壓。這種反差可補償快刀伺服刀架中存在的遲滯特性。

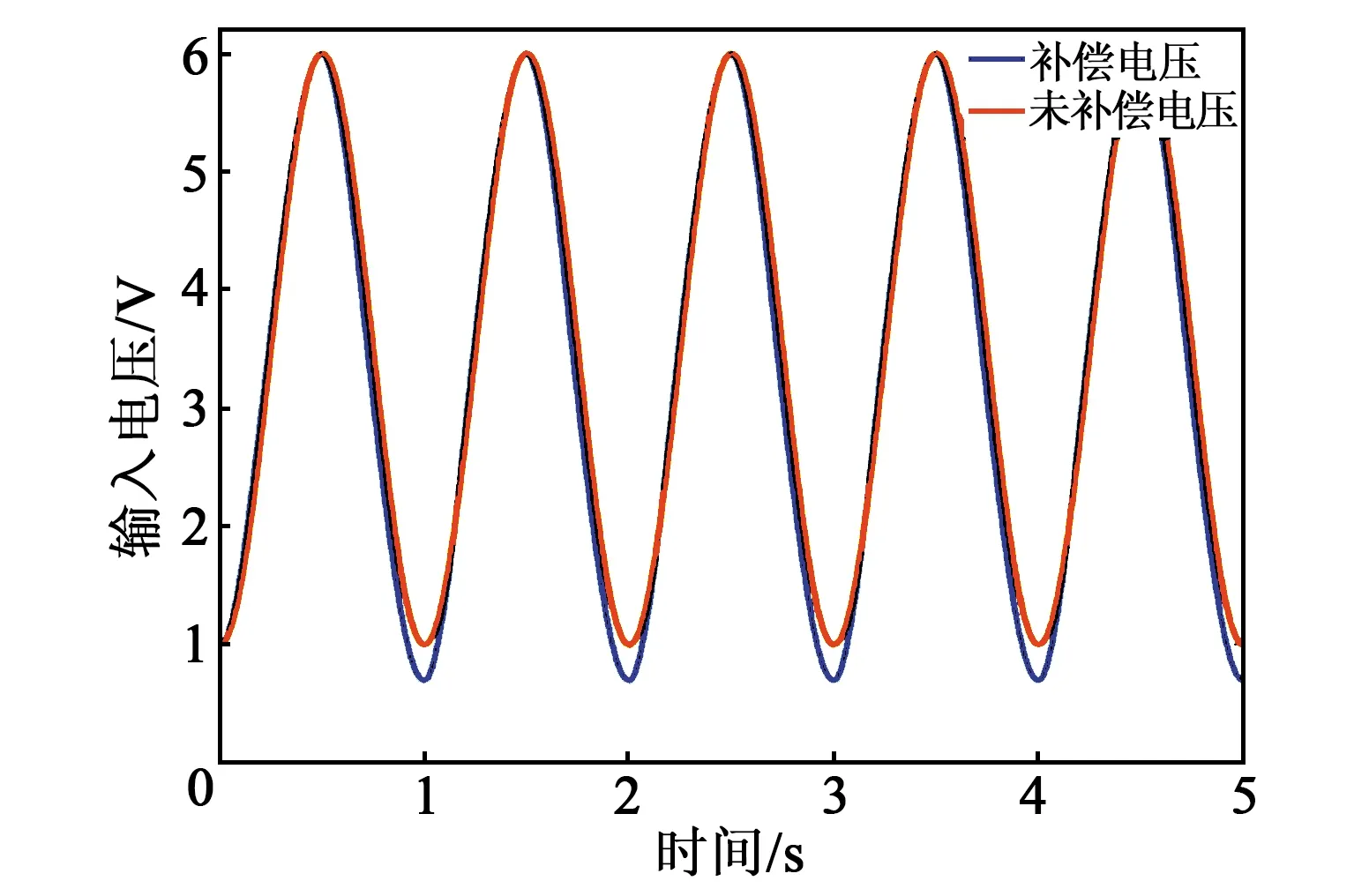
圖5 電壓對比圖

通過激光位移傳感器測得消除遲滯后的位移，其與理想位移的對比如圖6所示。由圖可看出，前饋控制下快速伺服刀架的末端位移輸出與期望位移吻合,最大軌跡跟蹤誤差發生在初始時刻。計算得到期望與實驗的線性度為4.5%。由此可推斷，基于Bouc-Wen模型的前饋控制能有效地消除快速伺服刀架的遲滯效應，從而提高快速伺服刀架的運動定位精度。

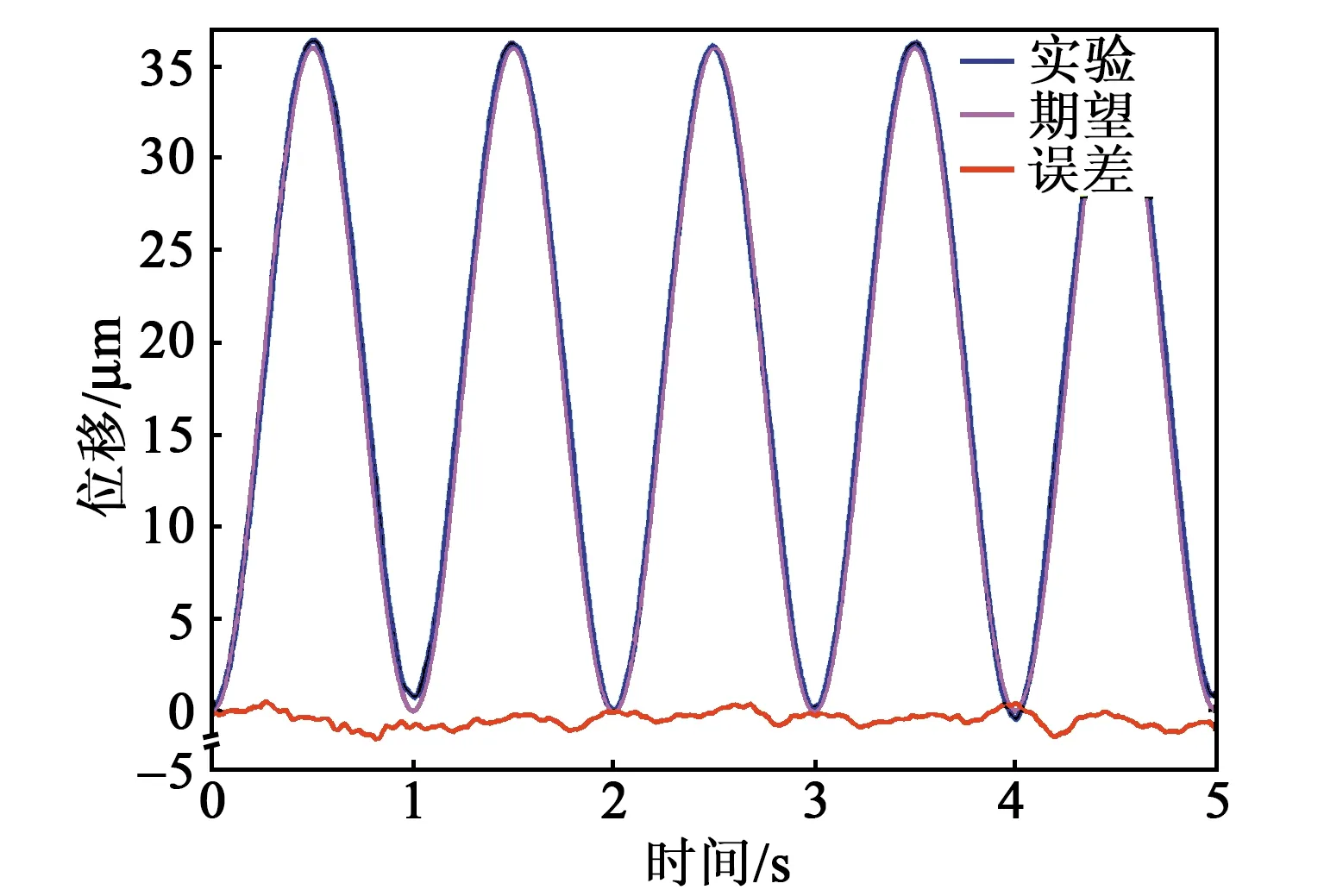
圖6 實驗位移曲線(正弦波)圖

為進一步驗證前饋補償法，執行了快速伺服刀架在變幅正弦波位移軌跡下的運動性能測試實驗。測得實驗曲線與期望位移如圖7所示。由圖可看出，遲滯補償下實驗位移消除了遲滯特性的影響，與理想位移基本吻合。再次證明了基于Bouc-Wen模型遲滯建模的前饋補償對快速伺服刀架中存在的遲滯特性消除的有效性

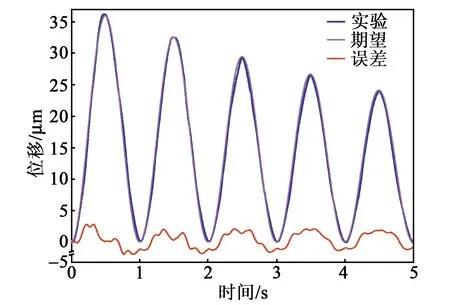
圖7 實驗位移曲線(變幅正弦波)圖

表2為基于歸一化Bouc-Wen模型的前饋補償控制在不同期望跟蹤位移下對快速伺服刀架定位精度的改善效果。由表可知，本文使用的基于歸一化Bouc-Wen遲滯模型的補償法能在很大程度上削弱由壓電陶瓷驅動器所引起的遲滯誤差，有效地提高了快速伺服刀架的驅動定位精度。為進一步提高快速伺服刀架的軌跡跟蹤精度及模型的穩定性，有必要引入反饋控制。

表2 不同驅動信號的誤差比較

5 二維性能測試

一些復雜曲面的加工要求快速伺服刀架能實現多維運動，因此，本文對提出的快速伺服刀架進行了兩自由度運動性能測試。為了實現兩自由度運動，兩個壓電陶瓷制動器分別安裝在x、y方向上。對每個方向上預緊的壓電陶瓷致動器施加特定電壓信號，最終快速伺服刀架的末端位移輸出曲線即是所選定的二維曲線。為了體現提出的快速伺服刀架二自由度運動性能，以圓軌跡為參考，選擇余弦信號驅動x方向的壓電陶瓷致動器A，正弦信號驅動y方向的壓電陶瓷致動器B。兩路激光位移傳感器同時測得兩個方向的快速伺服刀架末端的位移輸出，將測得位移作圖可獲得快速伺服刀架輸出的圓形軌跡。然而，由于壓電陶瓷致動器中存在的遲滯特性，導致了測得的軌跡更偏向于橢圓。因此，為獲取更精確的軌跡跟蹤，有必要在二自由度運動中引入前饋控制。將期望位移分解成兩個方向上的單向期望位移，并將其輸入Bouc-Wen逆模型中，求得兩個方向上的補償電壓。將求得的補償電壓作為輸入，可獲得了遲滯補償后的位移曲線。圖8為補償前、后快速伺服刀架輸出的二維曲線對比圖。

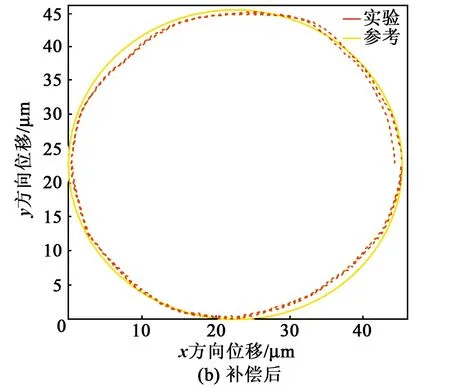
圖8 二自由度運動曲線圖

由圖8可看出，補償后二維軌跡曲線更接近于圓。而補償前曲線由于受遲滯特性的影響，在實驗位移x=0,y=45 μm或x=45 μm,y=0部分與參考軌跡偏差較大。補償前、后曲線在峰頂處偏差較大，一方面因受模型制約，另一方面因兩個方向的預緊力不同。以實驗與參考曲線對應點的歐式距離作為兩者之間適應度d的表征值，能對快速伺服刀架的二自由度運動性能進行定量分析。適應度d為

(11)

式中：xi,yi分別為由激光位移傳感器測得的x、y方向上的實驗位移；xri,yri為對應的參考曲線上點的位移。

將實驗數據代入式(11)可得到補償曲線的最大擬合誤差為4.486%，遠小于未補償曲線的最大擬合誤差(14.683%)。表明提出的二自由度快速伺服刀架在前饋控制的補償下具有較好的運動性能及優良的軌跡跟蹤能力。而引起誤差的原因，除控制模型本身存在的因素，兩個方向上存在的制造誤差也使輸出位移與期望位移不同。

6 結束語

由壓電陶瓷制動器驅動的快速伺服刀架具有頻率高及輸出力大等優點。但壓電材料中存在的遲滯特性嚴重影響了其輸出位移定位精度。簡化后的Bouc-Wen模型具有參數少及易取逆的優點，利用自適應遺傳算法可求得模型中的參數。實驗結果表明，歸一化后Bouc-Wen模型能很好地描述雙向壓電驅動的具有二自由度運動的快速伺服刀架中的遲滯現象。基于簡化后Bouc-Wen模型搭建了前饋控制環節，并對快速伺服刀架進行了運動性能測試。結果表明，在前饋控制的補償作用下，快速伺服刀架定位精度得到提高。同時，也證明了該快速伺服刀架具有優異的二自由度運動性能。