開口圓柱殼結構撓曲電傳感特性分析
張旭方,劉 麗,王鵬飛,傅佳宏(浙大城市學院 工程學院機械電子工程學系,浙江 杭州 310015)
0 引言
為了分析工程中常見的開口圓柱殼結構振動特性,需要各種振動傳感器。基于壓電材料的壓電傳感器是常見的振動傳感器,其利用壓電材料的力-電耦合特性,設計傳感器并進行傳感特性分析[1-6]。但壓電材料需預極化,使用時間過長,存在退極化現象。此外,壓電材料(如PZT陶瓷等)通常含有鉛元素,制備過程中會污染環境。因此,撓曲電材料作為一種新興的力電耦合智能材料而備受關注。
正撓曲電效應反映了應變梯度與電場間的力-電耦合關系。近年來研究者基于撓曲電材料進行了大量的理論與實驗研究,通過不同的理論與實驗方法確定各種撓曲電材料的正、逆撓曲電系數的大小[7-8]。研究撓曲電材料的撓曲電系數是為了更好地掌握材料特性,為進一步設計各種撓曲電器件以應用于不同的工程中提供了良好的基礎。
WANG等[9]論述了固體中的撓曲電效應近年來的發展、挑戰與前景,給出了宏觀與微觀撓曲電效應的理論發展時間軸和里程碑成就。由于撓曲電效應是與梯度有關的效應,撓曲電效應在納米微小尺度有廣泛的應用[10-12]。近年來,基于宏觀材料尺度的撓曲電效應引起了人們的關注。基于正撓曲電效應設計出各種撓曲電傳感器、俘能器等,并對智能結構進行傳感監測與能量采集研究[13-14]。HU等[15]已設計了基于一般雙曲率殼結構的撓曲電傳感器,根據不同結構的拉梅常數與曲率半徑可將該傳感器模型應用于不同的板殼結構。
基于正撓曲電效應,本文將建立基于開口圓柱殼結構的撓曲電傳感器模型。首先分析開口圓柱殼在外部激勵作用下的動態響應特性。根據正撓曲電效應建立撓曲電傳感理論,并推導出外部負載兩端的輸出模態電壓的表達式。當撓曲電片無限小時,基于撓電片的撓曲電傳感理論簡化為點的分布式傳感特性。最后分析了不同參數對撓曲電傳感信號的影響,對比不同方向彎曲應變引起的撓曲電信號的不同作用。
1 開口圓柱殼撓曲電傳感器模型
1.1 撓曲電傳感器模型
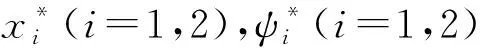
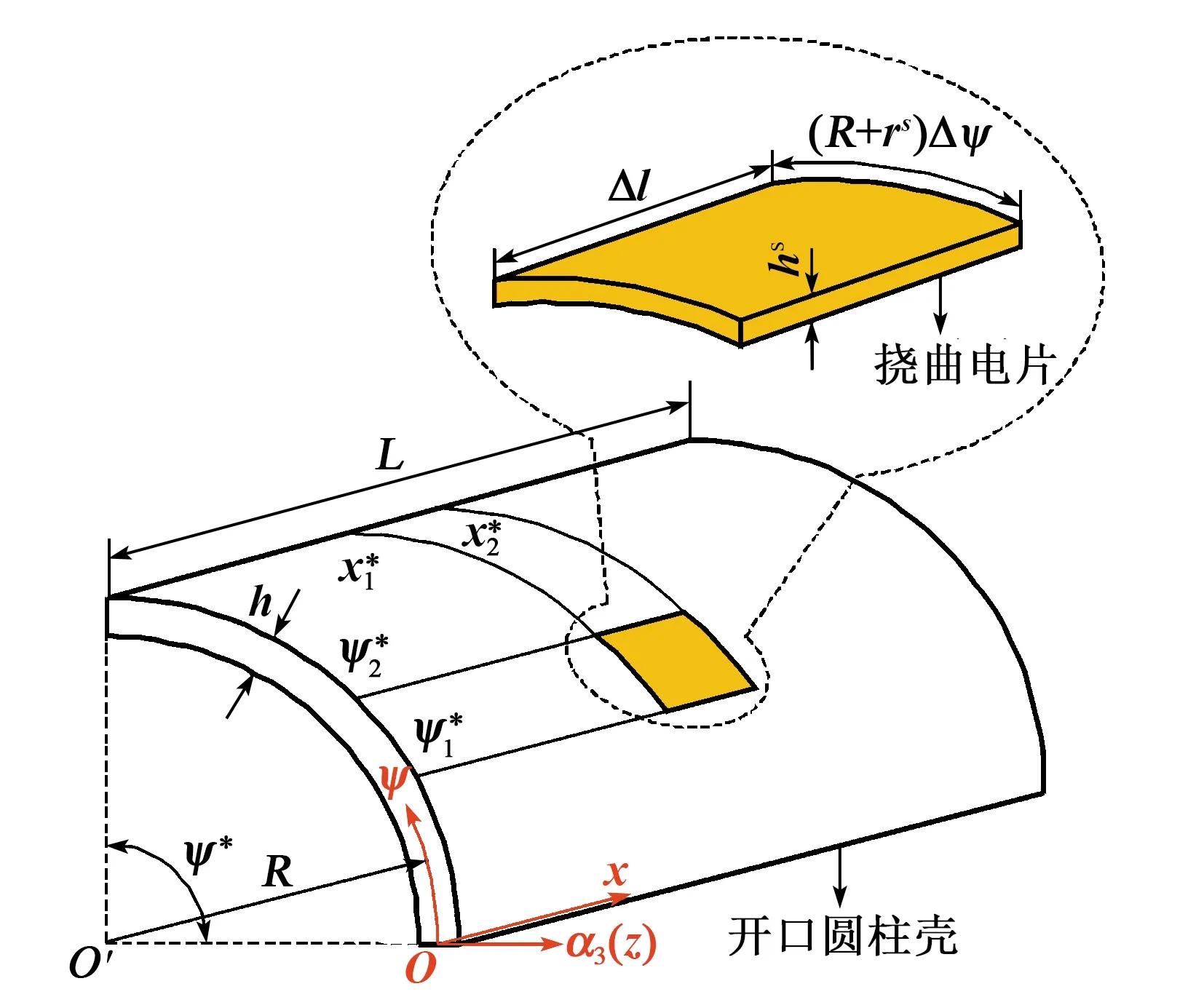
圖1 開口圓柱殼撓曲電傳感器模型
假設撓曲電片理想粘貼于開口圓柱殼的外表面上,根據Kirchhoff-Love薄殼理論,開口圓柱殼的應變[16]為
(1)

(2)

撓曲電效應主要與殼結構的應變梯度,即彎曲應變有關,彎曲應變為
(3)
(4)
1.2 撓曲電傳感器動態響應
根據模態擴展法,動態位移響應uψ、u3可用模態參與因子ηmn(t)和模態函數Uimn(x,ψ)(i=x,ψ)[17]表示為
(5)
(6)
式中:∑∑表示所有參與模態的疊加;m,n分別為長度、周向方向(x、ψ方向)的模態數;Uψmn(x,ψ),U3mn(x,ψ) (下文簡寫為Uψmn,U3mn)分別為周向與橫向振動的(m,n)階模態函數。
結構的模態函數取決于結構的邊界條件與結構尺寸。當開口圓柱殼四邊簡支時,結構的周向與橫向振動模態函數[17-18]可表示為
(7)
(8)
式中B,C分別為模態函數的幅值。
ηmn(t)揭示了每階模態振動響應在總的振動響應中所占比,模態參與因子的大小與每階模態力的大小相關。當結構邊界條件與尺寸確定后,模態陣型決定了傳感信號的分布特性,模態參與因子決定了傳感信號的大小幅值。
2 撓曲電傳感信號分析
基于正撓曲電效應,不同方向的應變梯度在法向的梯度引起了法向的電位移。根據一般雙曲率殼結構的撓曲電傳感公式[15],代入開口圓柱殼的曲率半徑R與拉梅常數可得:
μ12(kxx+kψψ)+ε33E3
(9)
式中:μ12為撓曲電系數;ε33為介電常數;E3為法向電場強度。
通過將電位移在有效的傳感面積Se上積分,求出開路狀態下的信號電壓[15]為

(10)
式中t為時間。
考慮每階模態在共振狀態下的傳感信號,則(m,n)階模態的模態電壓[15]可表示為
(φmn)xx+(φmn)ψψ
(11)
對于撓曲電傳感信號,模態電壓信號φmn可分成(φmn)xx與(φmn)ψψ,分別表示為
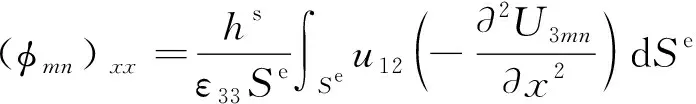
(12)
(13)
(14)
(15)
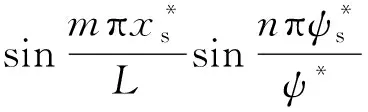
(16)
式中Lψ=Rψ*為開口圓柱殼圓周方向的長度。
根據式(14)~(16)可知,不同點對應的傳感信號表示開口圓柱殼不同位置的傳感信號。
3 變曲率開口圓柱殼分析
當L和Lψ保持不變時,ψ*對撓曲電傳感特性有影響。Rψ*=Lψ保持不變時,此時ψ*與R成反比。y*=150°、120°、90°、60°、 30°時,R為Lψ/ψ*(見圖2)。
當L和邊界條件固定時,不同的ψ*對應的結構頻率不同。每階模態的固有頻率分別為
(17)
(18)
(19)
(20)
(21)
(22)
(23)
a2=[1/(ρh)2](k11k33+k22k33+k11k22-
(24)
2k12k23k13-k11k22k33)
(25)
(26)
(27)
f1mn=ω1mn/2π
(28)
式中:ρ為板質量密度;Y為板楊氏模量;μ為泊松比;K為彎曲剛度;kij(i=1~3,j=1~3)、ai(i=1~3)、α均為求解過程中的系數ω1mn、f1mn為結構橫向振動的固有頻率。
4 數值仿真與優化
本文開口圓柱殼采用聚丙烯材料,撓曲電片使用a-聚偏氟乙烯(PVDF)薄膜材料。開口圓柱殼結構及撓曲電片的尺寸、材料參數如表1所示。
4.1 頻率分析
討論開口圓柱殼的撓曲電傳感特性需首先明確開口圓柱殼結構每階模態的固有頻率。結構的固有頻率越大,在相同模態力作用下,結構的振動響應越小。根據結構尺寸與參數,不同模態及彎曲角度下固有頻率分布如圖3所示。
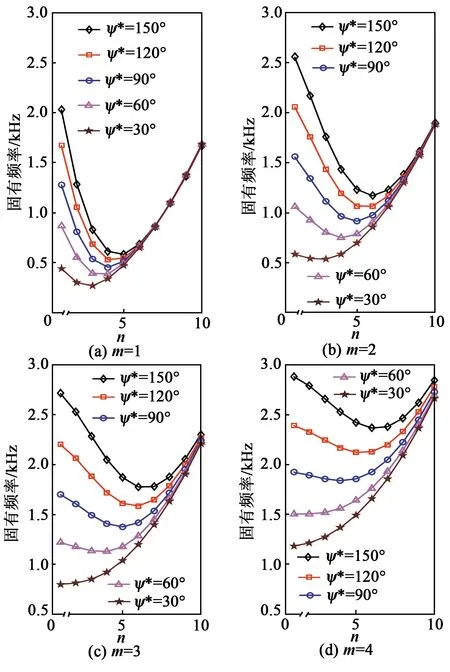
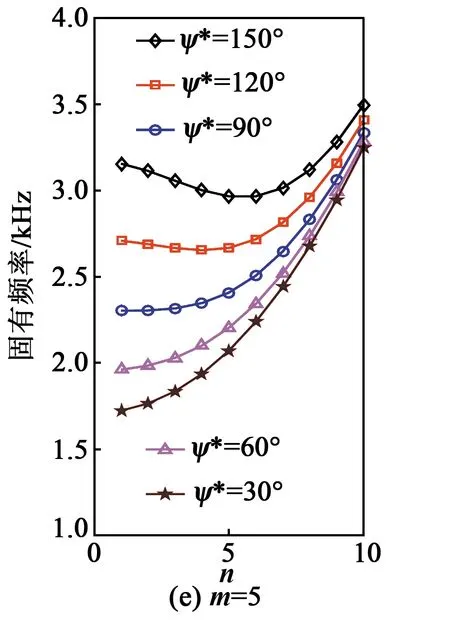
圖3 不同模態下不同曲率的固有頻率分析
由圖3可看出:
1) 當m保持不變時,隨著n增大,固有頻率先減小再增大。ψ*越大,固有頻率越大。即同樣尺寸的開口圓柱殼結構周向越彎,固有頻率越大,相同力作用下越難被激勵,響應越小。
2) 當m增大時,n與ψ*下的固有頻率增大,固有頻率的變化趨勢類似。m越大(如m=5),ψ*越小。當開口圓柱殼周向越平(如ψ*=30°)時,固有頻率隨著n的增大而增大,即模態數越大,頻率越大。
4.2 撓曲電傳感特性分析
當ψ*=150°時,模態函數的幅值B、C分別為-1、1。模態分別為(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)時撓曲電傳感特性如圖4、5所示。

圖4 m=1、n不同時撓曲電傳感特性
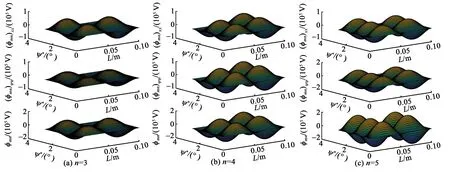
圖5 m=2、n不同時撓曲電傳感特性
不同模態下撓曲電傳感特性與模態的陣型有關。由圖4可知,(φmn)xx較小, (φmn)ψψ占主導。對比圖4、5可知,隨著m的增大, (φmn)xx增強。
4.3 不同曲率對撓曲電傳感特性影響
當L確定時,開口圓柱殼撓曲電傳感器的傳感特性與ψ*有關。不同模態下,分布式傳感特性如圖6所示。
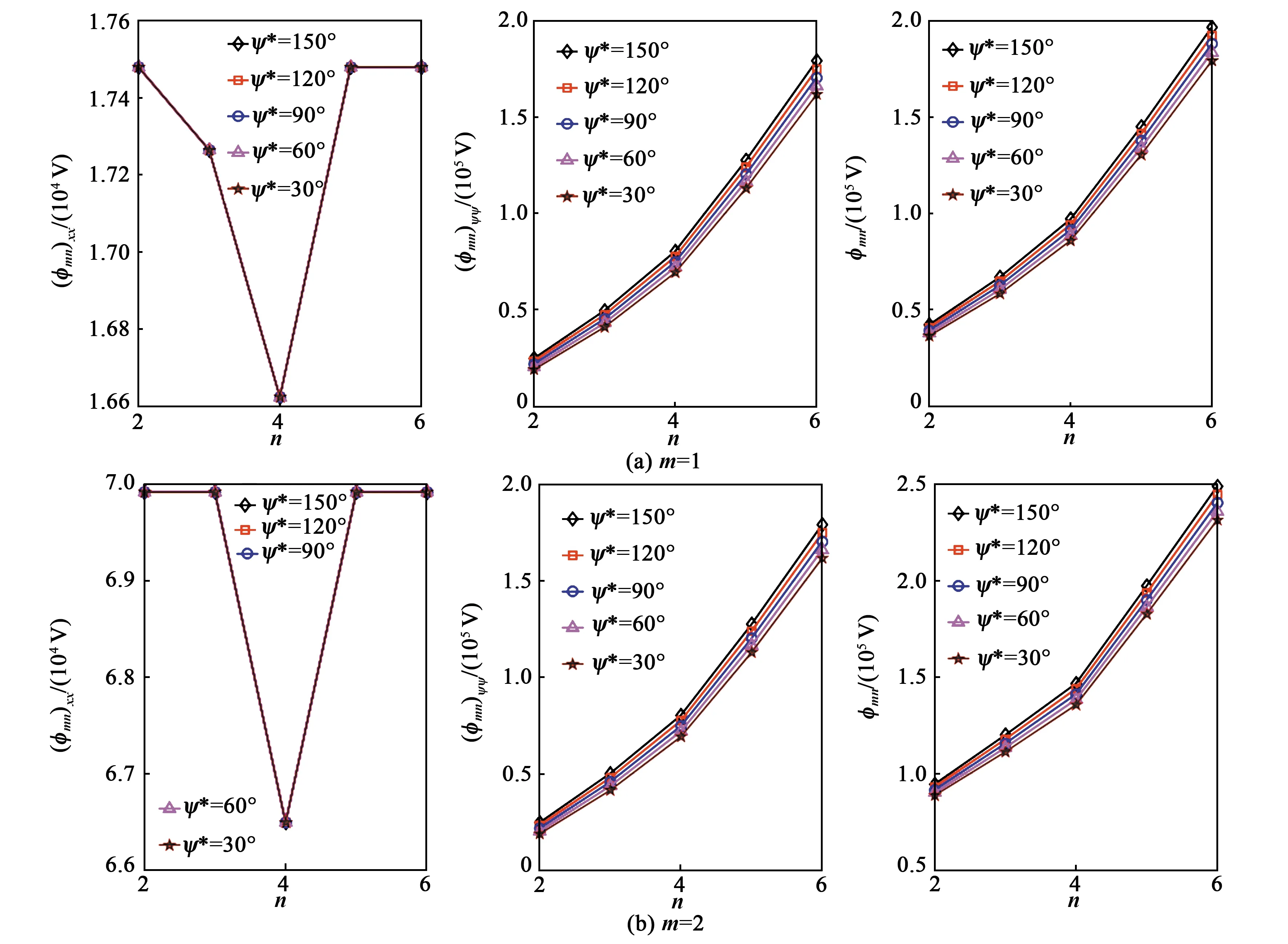
圖6 不同ψ*的模態電壓
當m=1或2且保持不變時, (φmn)xx不隨ψ*的變化而變化。 (φmn)ψψ隨著ψ*增大而增大,且隨著n的增加而增大。彎曲角度與模態數越大,kψψ越大,則 (φmn)ψψ越大。
隨著ψ*的增加,總彎曲應變引起的撓曲電傳感信號增大;隨著n增加,總彎曲應變引起的撓曲電傳感信號增大。總彎曲應變作用中,kψψ占主導作用。
5 結論
本文基于正撓曲電效應建立了開口圓柱殼結構的撓曲電傳感器模型,并分析了開口圓柱殼的撓曲電傳感特性,討論了不同的參數對傳感特性的影響。根據分析結果可得如下結論:
1) 不同模態下固有頻率不同,m不變時,隨著n的增加,固有頻率先減小再增加。
2) 隨著周向方向彎曲角度的增大,固有頻率增大。即周向越彎,固有頻率越大,相同力越不易被激勵。
3) 當m不變時,周向方向彎曲應變引起的撓曲電信號占主導,且撓曲電傳感信號隨著n的增加而變大。
4) 隨著周向彎曲角度的增大,周向方向的彎曲應變引起的撓曲電信號增大,即周向方向越彎,圓周方向的應變梯度越大,引起的撓曲電傳感信號越大。

