基于Floyd算法的裂隙巖質斜坡穩定性分析

蘭志廣，陳潤橋，聶細江，郭 猛，劉明亮

(天津市勘察設計院集團有限公司,天津 300191)

1 概述

裂隙巖質斜坡的穩定性多由賦存于坡體內的裂隙決定[1]。而由于裂隙的各向異性以及空間復雜性，針對裂隙巖質斜坡的穩定性研究仍十分困難。目前，針對裂隙巖質斜坡穩定性研究通常包括最危險滑動面的確定以及安全系數計算[2]。許多學者采用動態規劃法或者智能算法來確定危險滑動面，并取得理想結果。如張文等[3-4]考慮裂隙的隨機性，綜合采用改進的隨機動力學法、裂隙頻率法以及Dijkstra最短路徑算法確定了裂隙巖質斜坡的最危險滑動面；徐佩華等[5-6]考慮裂隙巖質斜坡的應力場特征，采用遺傳算法確定了最危險滑動面；段榮福[7]采用不平衡推力法計算出每個可能剪出口的剩余下滑力，結合最優理論法確定了斜坡最危險滑動面。在確定最危險滑動面之后，就可以根據最危險滑動面上巖土體的抗剪強度參數來計算裂隙巖質斜坡的安全系數。此外，隨計算機技術發展，裂隙巖質斜坡穩定性數值分析也取得迅速發展與廣泛應用。如Grifiths，Nour等[8-9]利用有限元模型確定斜坡的最危險滑動面并計算出安全系數；韓建國[10]基于有限差分法，利用強度折減法對裂隙巖質斜坡穩定性及破壞模式進行了評價；程謙恭等[11]利用離散單元法模擬評價裂隙巖質斜坡穩定性。

盡管針對裂隙巖質斜坡的穩定性研究取得了許多成果，但綜合考慮裂隙發育特征并合理確定裂隙巖質斜坡安全系數的方法仍然較少。本文提出了一種基于裂隙網絡模擬技術及Floyd算法的裂隙巖質斜坡穩定性分析方法。該方法首先根據現場裂隙發育特征模擬生成主滑面二維裂隙網絡，然后采用Floyd算法搜索不同剪入-剪出口之間的危險滑動面，最后利用傳遞系數法計算所搜索的危險滑動面的安全系數，以最小的安全系數作為對裂隙巖質斜坡整體穩定性的評估。

2 裂隙網絡模擬

根據巖體結構控制論，巖體穩定性是由賦存于巖體內部的結構面控制的[12]。因此，在裂隙巖質斜坡穩定性分析前，首先要分析斜坡巖體內裂隙的特征信息。本研究方法是在二維尺度上分析評價裂隙巖質斜坡穩定性，首先要獲得斜坡主滑面二維裂隙網絡。在實踐中，主滑面上的裂隙網絡通常難以調查到，因此需要根據露頭面裂隙信息模擬生成主滑面二維裂隙網絡(見圖1)。具體介紹如下。

2.1 三維裂隙網絡模擬

三維裂隙網絡模擬技術是近半個世紀以來不斷發展和完善用以表征巖體內部裂隙發育特征的最有效方法。該方法是基于現場實測裂隙數據，通過統計其跡長、產狀、密度等參數的概率分布類型，采用Monte Carlo模擬生成與現場裂隙統計相似的數學模型[13]。

裂隙巖質斜坡巖體內部三維裂隙網絡模擬主要步驟為：

1)裂隙位置模擬。

通常，采用泊松分布的方法在三維空間內生成裂隙幾何中心的坐標點。

2)裂隙尺寸模擬。

迄今為止，裂隙形狀尚未有統一定論，因此常假設裂隙形狀為圓盤、多邊形等。為簡化建模程序，在工程實踐中，常將裂隙形狀假設為圓盤。基于裂隙形狀為圓盤的假設，裂隙尺寸用圓盤直徑表征。裂隙直徑一般服從正態分布、對數正態分布以及伽馬分布。

3)裂隙產狀模擬。

裂隙產狀通常服從Fisher分布、Bingham分布、雙變量正態分布以及經驗分布。

4)裂隙密度確定。

采用測線法可以獲得裂隙間距，基于此，可推導出三維空間內裂隙密度。

5)Monte Carlo模擬。

采用Monte Carlo模擬對上述各項參數進行融合，即可生成與現場實測裂隙具有相似統計特征的三維裂隙網絡模型。

2.2 主滑面二維裂隙網絡生成

基于裂隙為圓盤的假設，并忽略裂隙的空隙及其起伏，那么決定裂隙圓盤位置、大小與形態的參數有圓盤中心點的坐標(xc，yc，zc)、圓盤直徑D以及裂隙的傾向α與傾角β，以這些參數即可表達三維裂隙網絡模型內的裂隙圓盤。選擇主滑面與三維裂隙網絡模型相截切，即可得到主滑面上的二維裂隙網絡。具體地，主滑面二維裂隙網絡數學模型表達式為：

(1)

其中,A=sinβcosα;B=sinαcosβ;C=cosβ;θ為斜坡主滑面走向;(x0,y0)為斜坡主滑面任一點在三維裂隙網絡中的坐標。

3 基于Floyd算法搜索危險滑動面

由于裂隙的強度參數相較巖石的強度參數小得多,因此在裂隙巖質斜坡滑動破壞時,滑動面往往沿著預先存在的裂隙擴展。斜坡滑動面經過的裂隙越多,抗滑力越小。當我們限定滑動面的剪入口與剪出口時,滑動路徑的總長度越小,經過的裂隙長度越大,則沿著此路徑滑動時所受的抗剪力越小。當滑動路徑最短時,則最大可能的經過了巖體中的裂隙,沿此路徑滑動時所受的抗剪力最小。由此分析可知,裂隙巖質斜坡危險滑動面的滑動主要沿剪入口與剪出口之間的最短路徑。搜索最短路徑的方法有很多種,由于Floyd算法容易理解,可以算出任意兩個節點之間的最短距離且代碼編寫也很簡單,因此我們采用Floyd算法搜索最短路徑(即危險滑動面)。Floyd算法具體介紹如下:

通過Floyd算法計算各個節點之間的最短路徑時,需要引入兩個矩陣(矩陣D和矩陣P),矩陣D中的元素d[i][j]表示節點i(第i個節點)到節點j(第j個節點)之間的距離;矩陣P中的元素p[i][j]表示節點i到節點j經過了p[i][j]記錄的值所表示的節點。假設有N個節點,則需要對矩陣D和矩陣P進行N次更新。初始時,矩陣D中節點d[i][j]的距離為節點i到節點j的權值;如果i和j不相鄰,則d[i][j]=∞,矩陣P的值為節點p[i][j]的j值。接下來開始對矩陣D進行N次更新。第1次更新時,如果“d[i][j]的距離”> “d[i][0]+d[0][j]” (d[i][0]+d[0][j]表示i與j之間經過第1個節點的距離),則更新d[i][j]為“d[i][0]+d[0][j]”,更新p[i][j]=p[i][0]。同理,第k次更新時,如果“d[i][j]的距離”> “d[i][k-1]+d[k-1][j]”,則更新d[i][j]為“d[i][k-1]+d[k-1][j]”,p[i][j]=p[i][k-1]。更新N次之后,算法完成,結合矩陣D和矩陣P即可獲得任意兩節點的最短路徑。

以圖2所示節點為例,應用Floyd算法計算節點a與節點d之間的最短路徑,通過更新矩陣D和矩陣P,可得到a→d之間的最短路徑為a→c→d,最短距離為3+1=4。

由于Floyd算法針對節點進行搜索,故在實際搜索時,需將主滑面二維裂隙網絡中的裂隙跡線進行離散化。裂隙跡線離散化程度越高,搜索結果越精確,但計算量也越大。此外,在實際搜索時,也需要預先對滑動面剪入口與剪出口進行設定。在實際斜坡滑動時,危險滑動面會優先選擇剪入口與剪出口處發育的裂隙,故在實際搜索過程中,將二維裂隙網絡的邊界假設為裂隙。離散化程度隨主滑面尺寸而定。

4 傳遞系數法計算安全系數

得到斜坡危險滑動面后,我們可以根據GB 50330—2013建筑邊坡工程技術規范計算斜坡的安全系數。由于基于Floyd算法搜索所得的危險滑動面形態為折線形,故采用傳遞系數法進行斜坡安全系數計算。

根據傳遞系數法(見圖3),斜坡安全系數(Fs)可按下列公式計算:

Ri=Wicosαitanφi+cili。

Ti=Wisinαi。

Ψj=cos(αi-αi+1)-sin(αi-αi+1)tanφi+1。

其中，Ri為第i計算條塊單位寬度重力引起的抗滑力;Ti為第i計算條塊單位寬度重力引起的下滑力;Ψj為第i計算條塊對第i+1計算條塊的傳遞系數;ci為第i計算條塊滑面的黏聚力;φi為第i計算條塊滑面的內摩擦角;li為第i計算條塊滑面的長度;αi為第i計算條塊滑面的傾角。

5 舉例分析

應用上述方法對某裂隙巖質斜坡進行穩定性分析。該裂隙巖質斜坡特征以陡峻地形為主,坡腳、坡頂地形相對高差86 m,斜坡坡面平均產狀為30°∠65°。坡面多為基巖出露,巖性主要為閃長巖,表現為塊狀構造,主要成分為白色的斜長石和深色的角閃石。此外,長期受內外動力地質作用的影響,坡面巖體結構破碎,節理裂隙十分發育。

通過分析測量所得420條裂隙的跡長及產狀信息,并采用動態聚類法進行分析,可將其劃分為三個優勢組,產狀分別為150°∠71°，89°∠43°和339°∠42°。據此確定裂隙的概率分布類型,見表1。

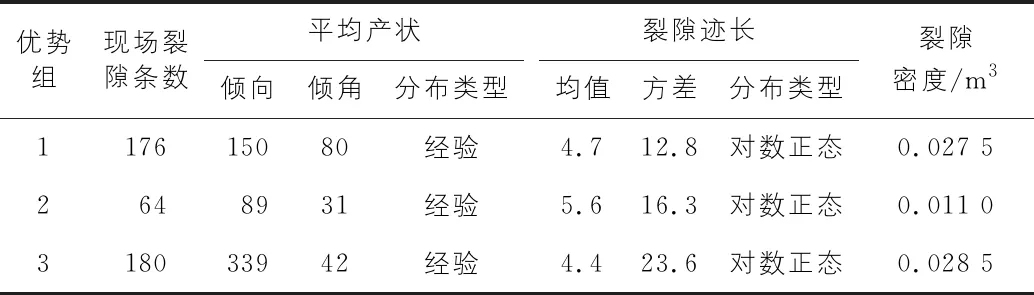
表1 裂隙優勢組主要參數匯總

對現場取樣巖石進行室內實驗,確定巖石黏聚力為24.6 MPa、內摩擦角為53°、巖石密度為2.8 g/cm3;對于裂隙強度參數,由于現場裂隙基本閉合且無填充,故黏聚力為0,裂隙內摩擦角采用基本內摩擦角,參照Brideau[14]研究取值為27°。

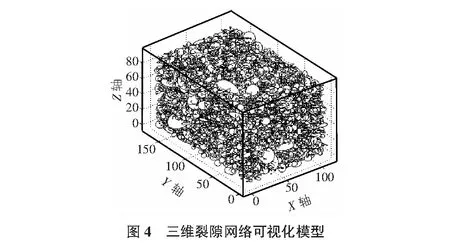
采用三維裂隙網絡模擬技術,對該裂隙巖質斜坡巖體內裂隙進行模擬。最終,模擬一個尺寸為110 m(X軸)×170 m(Y軸)×90 m(Z軸)的三維裂隙網絡,其可視化模型見圖4。現場調查該裂隙巖質斜坡可能沿臨空方向滑出,因此我們選取垂直于斜坡露頭面走向的鉛直平面為斜坡主滑面,并以此面截切三維裂隙網絡得到該裂隙巖質斜坡主滑面的二維裂隙網絡(見圖5)。

采用Floyd算法對該裂隙巖質斜坡進行危險滑動面搜索時,為保證搜索精度同時減少計算量,統一將主滑面二維裂隙網絡中的每一條裂隙跡線離散成5個節點(4等分);將主滑面二維裂隙網絡的邊界每隔10 m設置一個節點。最終,選取剪入口(60 m,86 m),(70 m,86 m),(80 m,86 m),(90 m,86 m),(100 m,86 m),(110 m,86 m)與剪出口(0 m,0 m),(4.66 m,10 m),(9.32 m,20 m),(13.99 m,30 m),(18.65 m,40 m),(23.32 m,50 m)進行分析。組合任一個剪入與剪出口,采用Floyd算法即可獲得36條危險滑動面(見圖6)。

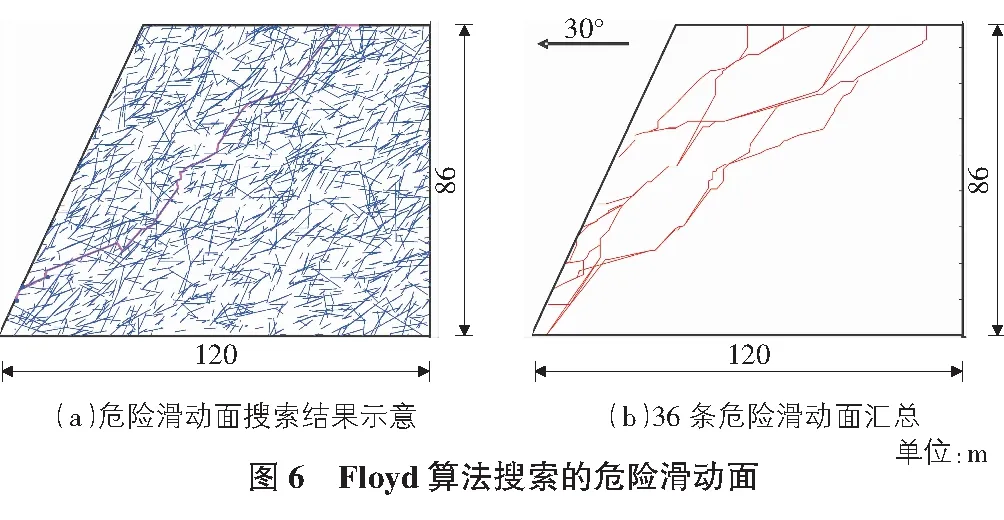
根據GB 50330—2013建筑邊坡工程技術規范,采用傳遞系數法對獲得的36條危險滑動面進行天然狀態下安全系數計算,結果如表2所示。

表2 各危險滑動面安全系數計算結果統計

由表2可知,不同剪入-剪出口組合之間危險滑動面所對應的安全系數不同。該裂隙巖質斜坡各危險滑動面最小安全系數為15.51,最大為68.37,均值為39.33。為保證工程安全性,選擇最小的安全系數作為對整個裂隙巖質斜坡穩定性的評估,則該裂隙巖質斜坡安全系數為15.51,故天然狀態下該裂隙巖質斜坡整體穩定性好。

6 結論

通過本研究提出的方法,針對某裂隙巖質斜坡進行研究,最終可得到以下結論:

1)裂隙巖質斜坡危險滑動面往往沿著預先存在的裂隙擴展,因此裂隙巖質斜坡穩定性分析前必須考慮斜坡主滑面裂隙的發育特征。由于斜坡主滑面裂隙網絡在發生破壞前不可見,因而根據現場露頭面裂隙信息模擬生成與現場裂隙統計相似的數學地質模型的裂隙網絡模擬技術是裂隙巖質斜坡穩定性分析必不可缺的。

2)經分析,裂隙巖質斜坡危險滑動面的滑動主要沿剪入口與剪出口之間的最短路徑。因而可視剪入口與剪出口之間的最短路徑為裂隙巖質斜坡的危險滑動面。Floyd算法可以簡單快速計算出任意兩個節點之間的最短路徑,因而能很好地被應用于裂隙巖質斜坡危險滑動面的搜索。

3)Floyd算法搜索得到的危險滑動面為折線形,因而可以采用傳遞系數法進行安全系數計算。不同危險滑動面對應的安全系數不同,選擇最小的安全系數對整個裂隙巖質斜坡穩定性進行評估。對于研究案例,天然狀態下安全系數為15.51,表明天然狀態下該裂隙巖質斜坡整體穩定性好。

4)本文研究案例僅針對選定剪入-剪出口組合進行危險滑動面搜索,計算所得最小安全系數與實際可能存在一定誤差,這個誤差可通過增密剪入-剪出口組合來消除或緩解。