基于三段式Halbach陣列的同軸磁性聯軸器優化設計

秦清海，汲柏良

(曲阜師范大學 工學院，日照 276800)

0 引 言

傳統的聯軸器存在對中問題，若對中不良，將導致振動與噪聲過大、轉軸彎曲以及軸承磨損等一系列故障，嚴重降低設備的可靠性，增加維修費用。為提高聯軸器的可靠性，有學者提出了一種基于磁力傳動的磁性聯軸器。由于該新型磁性聯軸器具有物理隔離性好、無機械接觸、可過載保護以及可靠性高的優勢，已成功應用于石油化工、半導體、生物醫藥等行業[1-2]。常見的磁性聯軸器有兩種，分別是同軸磁性聯軸器和平面磁性聯軸器。

在磁性聯軸器的理論分析與優化設計方面，許多學者進行了研究。文獻[3]介紹了同軸磁性聯軸器的結構特點并分析了影響其最大靜態轉矩的因素。文獻[4]針對磁力泵聯軸器推導出其由于端部漏磁損失的轉矩值，為樣機的研制過程提供了參考。文獻[5]將一種兩段式 Halbach永磁陣列應用于同軸磁性聯軸器，在同等條件下Halbach陣列磁性聯軸器的最大靜態轉矩提高了23.8%。理論證明該結構的磁性聯軸器無需軛鐵，可有效減小轉動部件的轉動慣量，縮短啟動時間。文獻[6]等推導了一種理想徑向Halbach轉子磁性聯軸器的三維解析轉矩方程，得出了峰值轉矩的產生條件。

有限元方法可有效應用于復雜電磁場問題的求解，但隨著網格剖分精度的提高，會出現計算效率低的問題。有限元方法和其它優化算法結合，用于各種電機拓撲的優化設計，是當下研究的熱點。文獻[7]將響應曲面法與遺傳算法相結合對微型電動車驅動電機的成本進行了優化。文獻[8]提出了基于自適應網格的有限元方法，采用多目標遺傳算法對不同類型的電機拓撲進行了優化。文獻[9]基于多目標粒子群算法對一臺永磁同步電機的效率、功率因數以及起動性能進行了優化。

本文將一種三段式Halbach陣列應用于同軸磁性聯軸器中，利用響應曲面法建立了永磁體轉矩密度與磁性聯軸器總體積的復合性能函數，并基于模擬退火(以下簡稱SA)算法對最優復合性能函數進行求解，得到了最佳的設計參數組合。仿真結果表明，優化后磁性聯軸器永磁體的轉矩密度得到了較大幅度的提升，磁性聯軸器的總體積有所減小，驗證了本文優化方案的有效性。

1 三段式Halbach陣列

傳統的同軸磁性聯軸器主要由內、外轉子磁齒輪以及固定于其表面的永磁體組成，其中永磁體采用徑向充磁方式，即N，S極交替排列的形式。圖1給出了同軸磁性聯軸器的拓撲結構以及重要尺寸標注。本文以一臺功率等級為10 kW的同軸磁性聯軸器為例進行說明，其技術指標如表1所示。其中，外轉子磁齒輪、內轉子磁齒輪分別作為主動軸與從動軸，外轉子永磁體生成的旋轉磁場與內轉子永磁體生成的磁場相互作用，驅動內轉子與外轉子同方向旋轉。為應對過載等不同工況，設定過載倍數為1.5，則該設計的最大靜態轉矩為286.5 N·m。

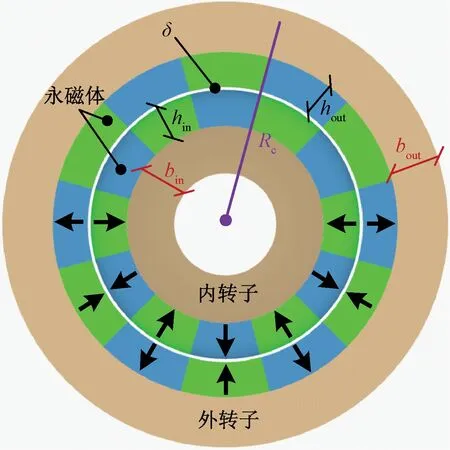
圖1 同軸磁性聯軸器的拓撲結構及相關參數

表1 10 kW同軸磁性聯軸器的技術指標

Halbach陣列是一種新型的永磁體排列方式，它通過將充磁方向不同的永磁體按照一定順序排列，可使氣隙側的磁場強度增強，達到節省永磁體材料、提高轉矩密度的目的。本文采用的三段式Halbach陣列如圖2所示。其中每個磁極都由一塊徑向充磁和兩塊充磁角度與其成45°的永磁體組成。

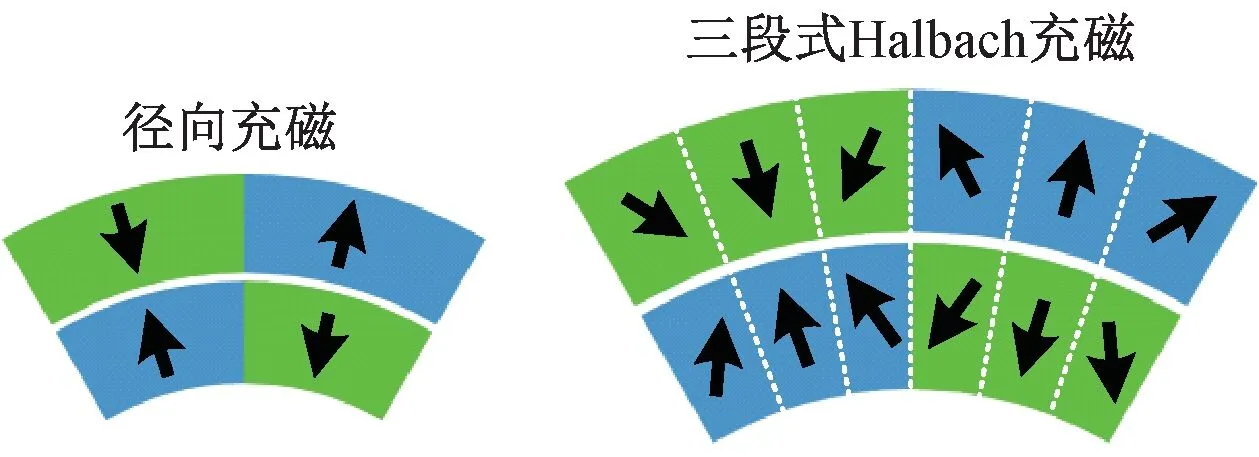
圖2 徑向充磁及三段式Halbach陣列

下面對采用Halbach陣列以及傳統的徑向充磁方式的同軸磁性聯軸器性能進行了比較。根據有限元仿真實驗，首先確定滿足設計要求下使用徑向充磁方式的技術指標各參數的初始值，如表2所示。保持表2中參數不變，將充磁方式改為Halbach陣列，采用兩種不同充磁方式的磁性聯軸器的磁力線分布對比如圖3所示。可以看出，采用三段式Halbach陣列后，內外轉子鐵心部分磁力線大部分集中在氣隙側，氣隙側的磁感應強度得到了加強，永磁體的利用率得到了顯著提高。

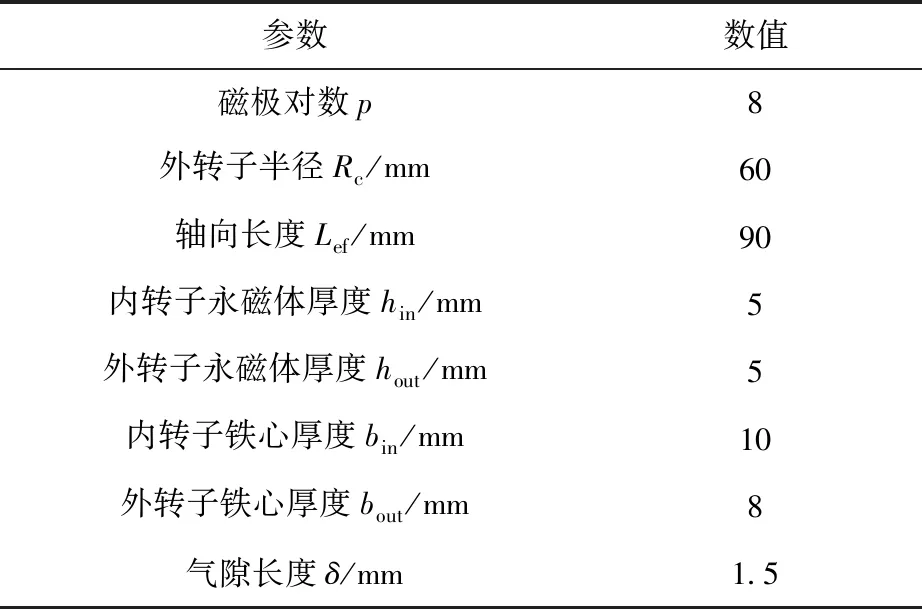
表2 各參數的初始值

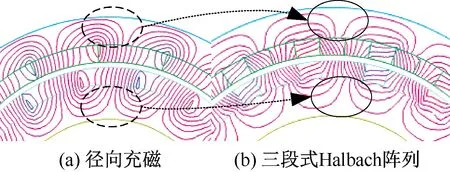
圖3 兩種充磁方式磁力線分布對比

圖4和圖5分別給出了兩種充磁方式下的氣隙磁密與其傅里葉分解的諧波對比圖。

由圖4可以看出，采用三段式Halbach陣列之后氣隙的徑向磁密與切向磁密幅值均有所上升，并且徑向磁密與切向磁密波形都具有8個波峰，這也說明了內外轉子的磁極對數為8。

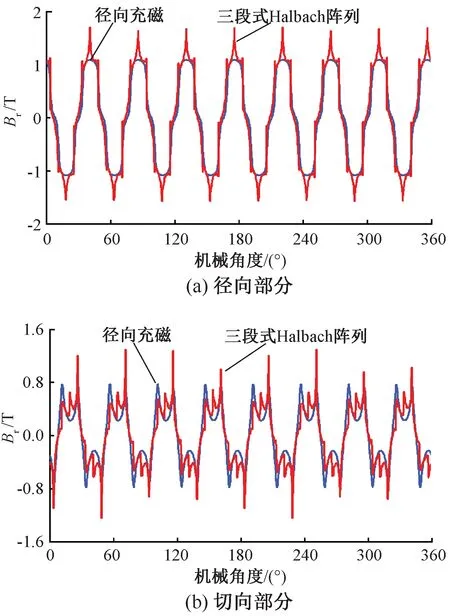
圖4 兩種充磁方式氣隙磁密波形對比

由圖5可以看出，兩種充磁方式下的氣隙磁密的諧波分量主要集中在基波(8對極)及其奇數倍諧波，而偶數次諧波含量很低。采用Halbach陣列后，徑向諧波分量中除基波分量外，3次(24對極)、7次(56對極)、9次(72對極)以及13次(104對極)諧波幅值也有所增加。而切向諧波分量中除基波分量外，7次(56對極)、13次(104對極)諧波幅值增加較為明顯。

圖5 兩種充磁方式氣隙磁場諧波對比

為定量研究三段式Halbach陣列對氣隙磁密的影響，表3給出了兩種充磁方式下幅值最高的前5組諧波徑向與切向分量的幅值。

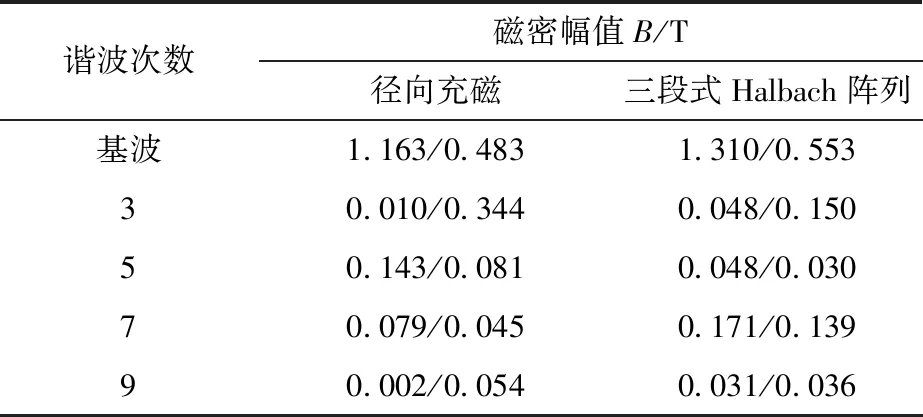
表3 兩種充磁方式下各次諧波分量徑向/切向磁密幅值

正弦波的波形質量通常用諧波畸變率THD衡量，其表達式：

(1)

式中：Bi為氣隙磁密的各次諧波幅值；B1為氣隙磁密的基波幅值。

由圖5可以看出，前9次諧波已經占據了諧波含量的絕大部分。由式(1)可計算兩種充磁方式下前9次諧波的徑向與切向分量的諧波畸變率。經過計算，采用三段式Halbach陣列之后，徑向分量的諧波畸變率由12.35%降低為5.27%，切向分量的諧波畸變率由73.24%降低為27.72%。這說明采用三段式Halbach陣列可有效提升氣隙磁密波形的正弦性。

磁場耦合在內轉子上產生的磁力轉矩可由麥克斯韋張量法求得[10]：

(2)

式中：μ0為真空磁導率；Lef為聯軸器的軸向長度；Rδ為氣隙半徑；Br、Bt分別為氣隙磁密的徑向與切向分量；θ為觀測點所對應的極角。

圖6給出了采用徑向充磁與三段式Halbach陣列的聯軸器內轉子靜態轉矩波形。可以看出，在相同的尺寸參數下，采用徑向充磁方式的內轉子最大靜態轉矩為286.5 N·m，而采用三段式Halbach陣列后最大靜態轉矩達到了369.7 N·m，提升了接近29%，說明采用三段式Halbach陣列可有效提升同軸磁性聯軸器的轉矩密度。

圖6 兩種充磁方式靜態轉矩對比

2 優化參數與優化目標選取

針對同軸磁性聯軸器的性能要求，一方面應在保證轉矩性能達到要求的前提下盡量減少永磁體用量，提高其轉矩密度、降低成本；二是受應用場景的限制，其總體體積不能過大，應設法提高其空間利用率。為此，選取磁性聯軸器永磁體的轉矩密度D以及磁性聯軸器的總體積V作為待優化目標。

永磁體轉矩密度D的計算公式如下：

(3)

式中：Tin為同軸磁性聯軸器內轉子的最大靜態轉矩；VPM_in、VPM_out分別表示內、外轉子永磁體的體積，其計算公式如下：

VPM_in=πLef[(Rc-bout-hout-δ)2-

(Rc-bout-hout-δ-hin)2]

(4)

VPM_out=πLef[(Rc-bout)2-(Rc-bout-hout)2]

(5)

式中：Rc、Lef分別為同軸磁性聯軸器的外轉子半徑與軸向長度；hin、hout分別內外轉子的永磁體厚度；bin、bout分別內外轉子的鐵心厚度；δ為氣隙長度。

同軸磁性聯軸器總體積V的計算公式如下：

(6)

最終選取待優化的設計變量為同軸磁性聯軸器外轉子半徑Rc、軸向長度Lef以及內、外轉子永磁體的厚度hin、hout。

其次，采用三段式Halbach陣列后，為達到相同的轉矩性能，對表2中的數值進行了初步優化，如表4所示。可以看出，在相同的轉矩性能下采用三段式Halbach陣列之后，同軸磁性聯軸器的軸向長度由90 mm減少為80 mm，永磁體厚度由5 mm減少為4.5 mm，通過進一步計算，永磁體的用量由0.313 8 dm3減少為0.243 7 dm3，減少了22.3%。

表4 各參數的初步優化值

3 基于響應曲面法的復合性能函數建模

響應曲面法(以下簡稱RSM)是一種基于數理統計的優化方法，它通過合理的實驗設計以及較少的實驗次數來獲取較多的有效信息，RSM被廣泛應用于機電設備的優化設計中[11-13]。

RSM實驗樣本數由下式確定：

N=2m+2m+1

(7)

式中：m=4為待優化的設計變量個數，N=25為RSM實驗樣本數。

基于表2中各參數的初始值，使用有限元軟件ANSYS進行RSM實驗，建立各優化目標與待優化的設計變量之間的二次回歸(以下簡稱QR)模型：

(8)

式中：f1(x)、f2(x)為目標函數，分別表示永磁體的轉矩密度D、同軸磁性聯軸器總體積V的倒數的預測值；x為由待設計變量組成的設計向量，即：x= [x1,x2,x3,x4]= [Rc,Lef,hin,hout]；α0、αm、αmn、β0、βm、βmn為回歸系數；κ1、κ2為隨機誤差。

圖7給出了設計變量關于轉矩密度D的響應結果。

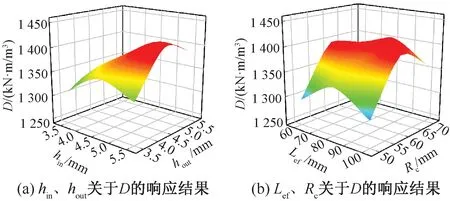
圖7 各設計變量關于轉矩密度D的響應結果

圖8給出了使用RSM與QR方法得出的永磁體轉矩密度D與同軸磁性聯軸器總體積倒數V-1的對比圖。判定系數R2定義為回歸變量的回歸平方和與總離差平方和的比值，其數值越接近1說明回歸精度越高。經過計算，兩者的判定系數分別為0.993 6與0.999 6，均高于0.99，說明回歸精度較高，結果較理想。

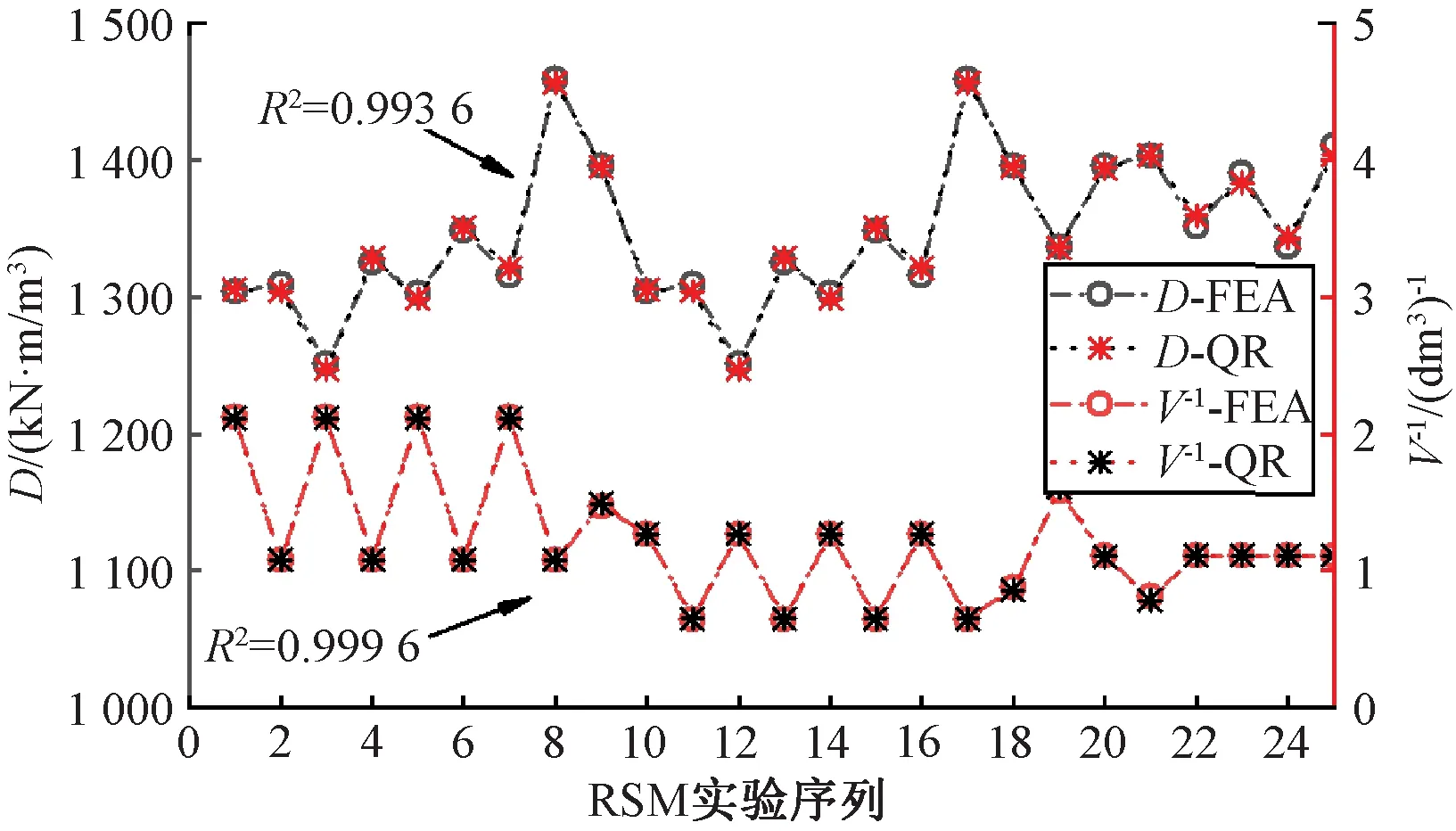
圖8 擬合結果對比

引入復合性能函數F(x)，根據圖7的實驗結果確定各設計參數的取值范圍，將研究問題轉化為下式的單目標非線性規劃問題：

maxF(x)=max[w1γ1f1(x)+w2γ2f2(x)+

λΦ-1(x,Tin0)]

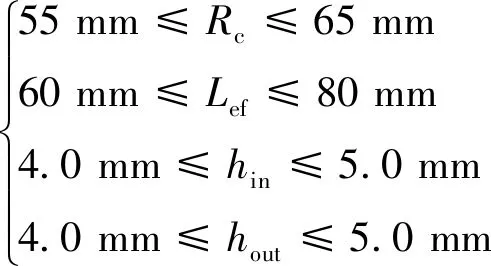
(9)

式中：F(x)為復合性能函數，它綜合考慮了設計變量對各性能指標的影響；w1、w2表示權重系數，且有w1+w2=1；γ1；γ2表示尺度系數，用于平衡不同性能指標之間量綱與量級的差異性；λΦ-1(x,Tin0)為懲罰項，用于將含函數約束(即目標轉矩約束)的優化問題轉化為無函數約束最優化問題；λ為懲罰因子；Φ-1(x,Tin0)為懲罰函數，其表達式如下：

(10)

式中：f3為內轉子最大靜態轉矩的預測值，其形式與式(8)中f1、f2的形式一致；Tin0為內轉子最大靜態轉矩的目標值，此處取值為286.5 N·m。

尺度系數γ1、γ2的計算公式如下式：

(11)

(12)

式中：Dmax、Dmin分別表示RSM實驗中永磁體轉矩密度D的最大值、最小值；Vmax、Vmin分別表示RSM實驗中同軸磁性聯軸器總體積V的最大值、最小值。

由于優化目標永磁體轉矩密度擬合結果的判定系數低于總體體積的倒數，因此給予前者較小的權重系數值，以降低回歸精度較低帶來的誤差，表5給出了權重系數與尺度系數的取值。

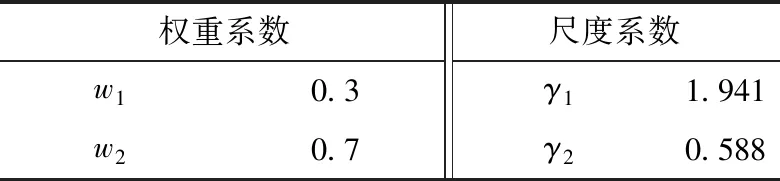
表5 權重系數與尺度系數的取值

4 SA算法尋優

SA算法相對于傳統的優化算法能夠以一定的概率接受比當前解要差的解，因此有較大可能性跳出局部最優解，達到全局最優解。且該法計算過程簡單、魯棒性強，可用于復雜非線性規劃問題的求解[14-15]。由于SA算法擅長無函數約束的目標優化問題，故在式(9)中引入了懲罰函數項，將其轉化為無函數約束的優化問題。設置迭代次數為1 000次，適應度函數取為-F(x)，懲罰因子λ=0.01，使用SA算法對式(9)進行求解。圖9給出了當前適應度函數與最優適應度函數的優化迭代過程。可以看出，在第500代時，適應度函數就已經收斂，最終的適應度函數為-2 832.65。

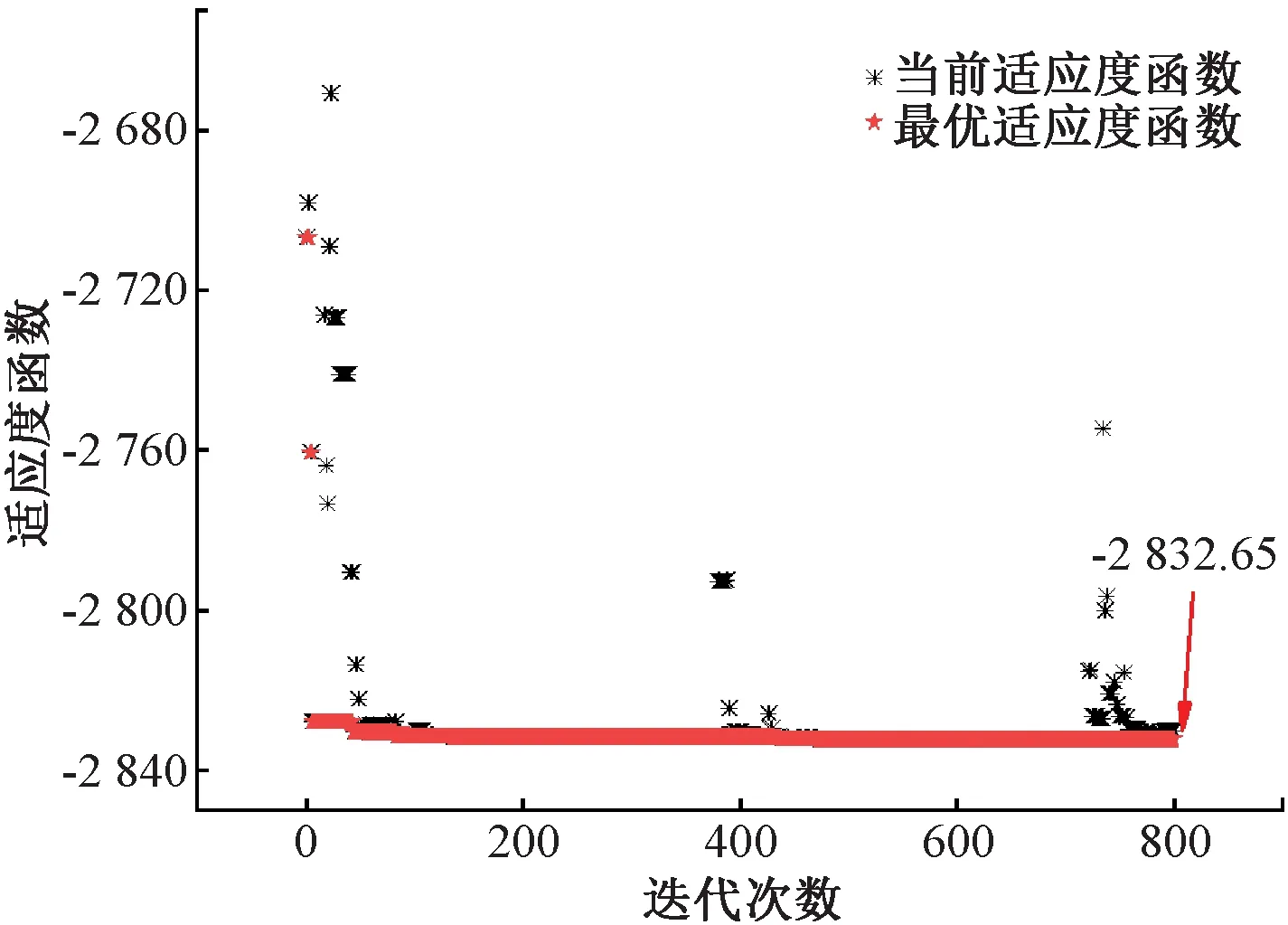
圖9 適應度函數的優化迭代過程

本文的同軸磁性聯軸器的優化設計流程圖如圖10所示。

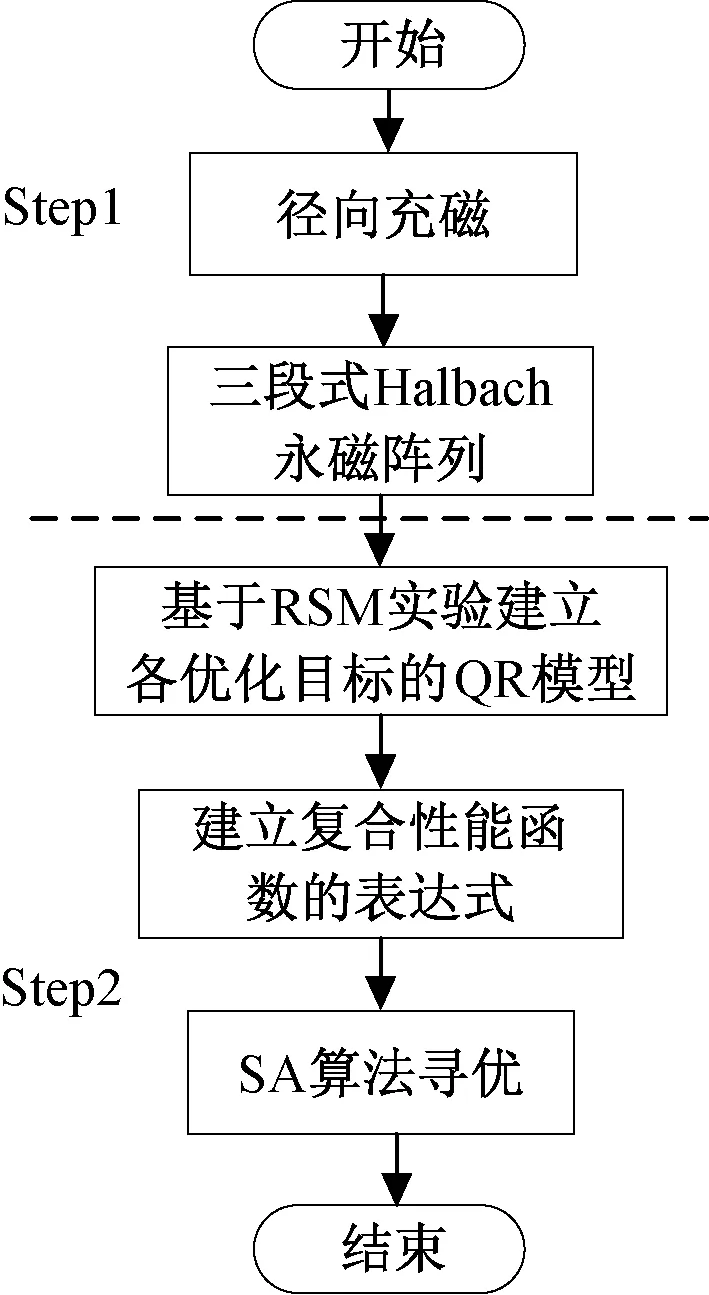
圖10 本文優化設計流程圖

表6給出了使用SA算法優化前后各參數的值，其中值3為優化后各參數的值。可以看出，采用三段式Halbach陣列的聯軸器經優化后，內、外轉子永磁體厚度有所增加，但軸向長度由80 mm減小為74.83 mm。

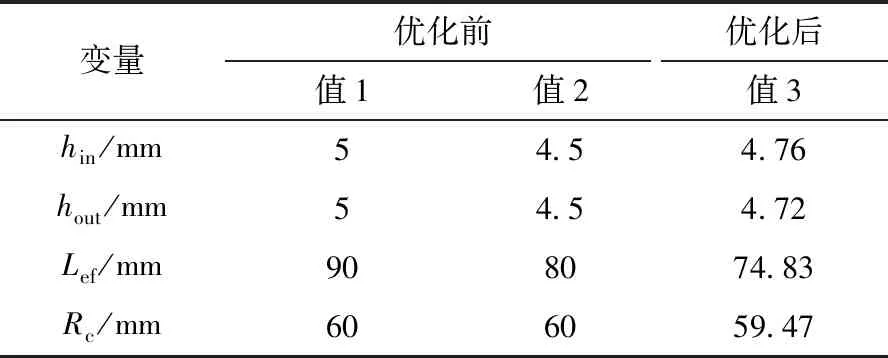
表6 各參數優化前后對比

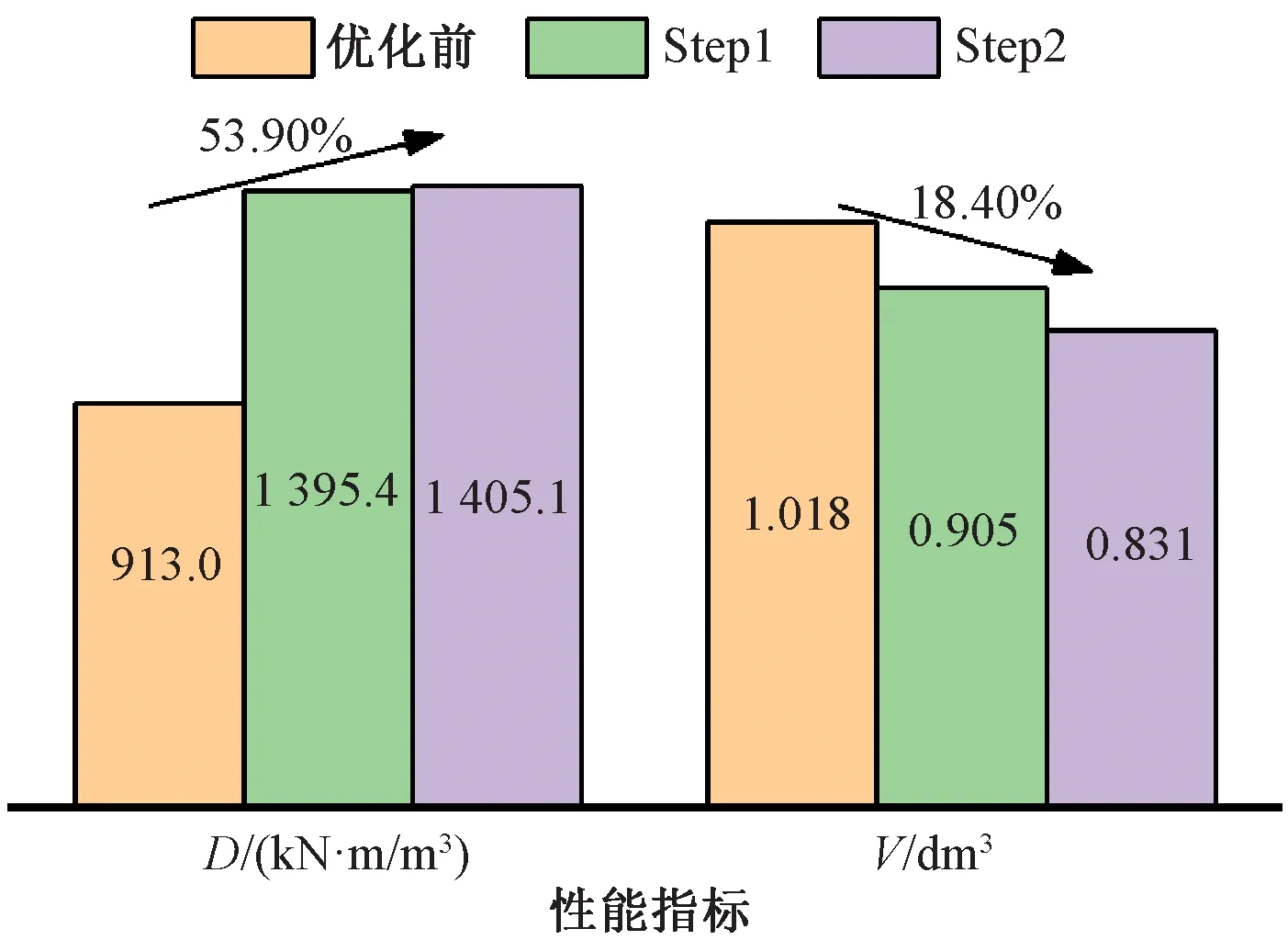
圖11 優化后磁性聯軸器各性能指標對比

圖11對圖10的設計流程各性能指標優化前后進行了比較。可以看出，永磁體轉矩密度由1 395.4 kN·m/m3提升至1 405.1 kN·m/m3，總體積由0.905 dm3減小為0.831 dm3，減小了8.2%。相對于原始的徑向充磁方式，優化后的永磁體轉矩密度提升了53.9%，聯軸器的總體積減小了18.4%。其中，永磁體轉矩密度大幅提升的主要原因是采用了三段式Halbach陣列。

圖12給出了優化前后同軸磁性聯軸器的3D模型圖。可以看出，優化后聯軸器的總體積和永磁體用量均有所減小，降低了成本、提高了空間利用率。

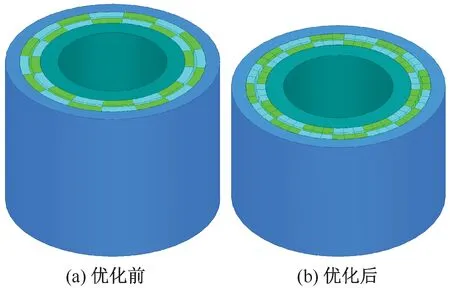
圖12 優化前后磁性聯軸器3D模型對比

圖13與圖14分別給出了優化后聯軸器的磁場強度分布云圖以及磁力線分布圖。可以看出，磁力線分布合理，漏磁較少，鐵心材料得到了充分利用。這充分說明了三段式Halbach陣列以及優化策略的有效性。

圖13 優化后的磁場強度分布云圖

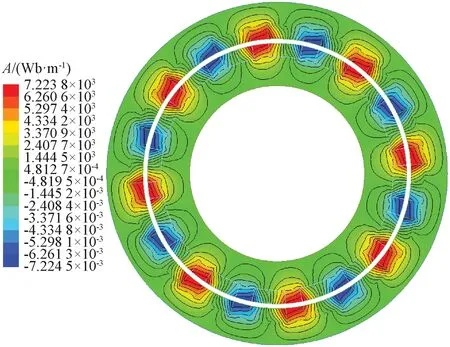
圖14 優化后的磁力線分布圖

圖15給出了優化前后磁性聯軸器內轉子的靜態轉矩波形對比。可以看出，優化前后最大靜態轉矩變化不大，滿足設計轉矩為289.5 N·m的要求。

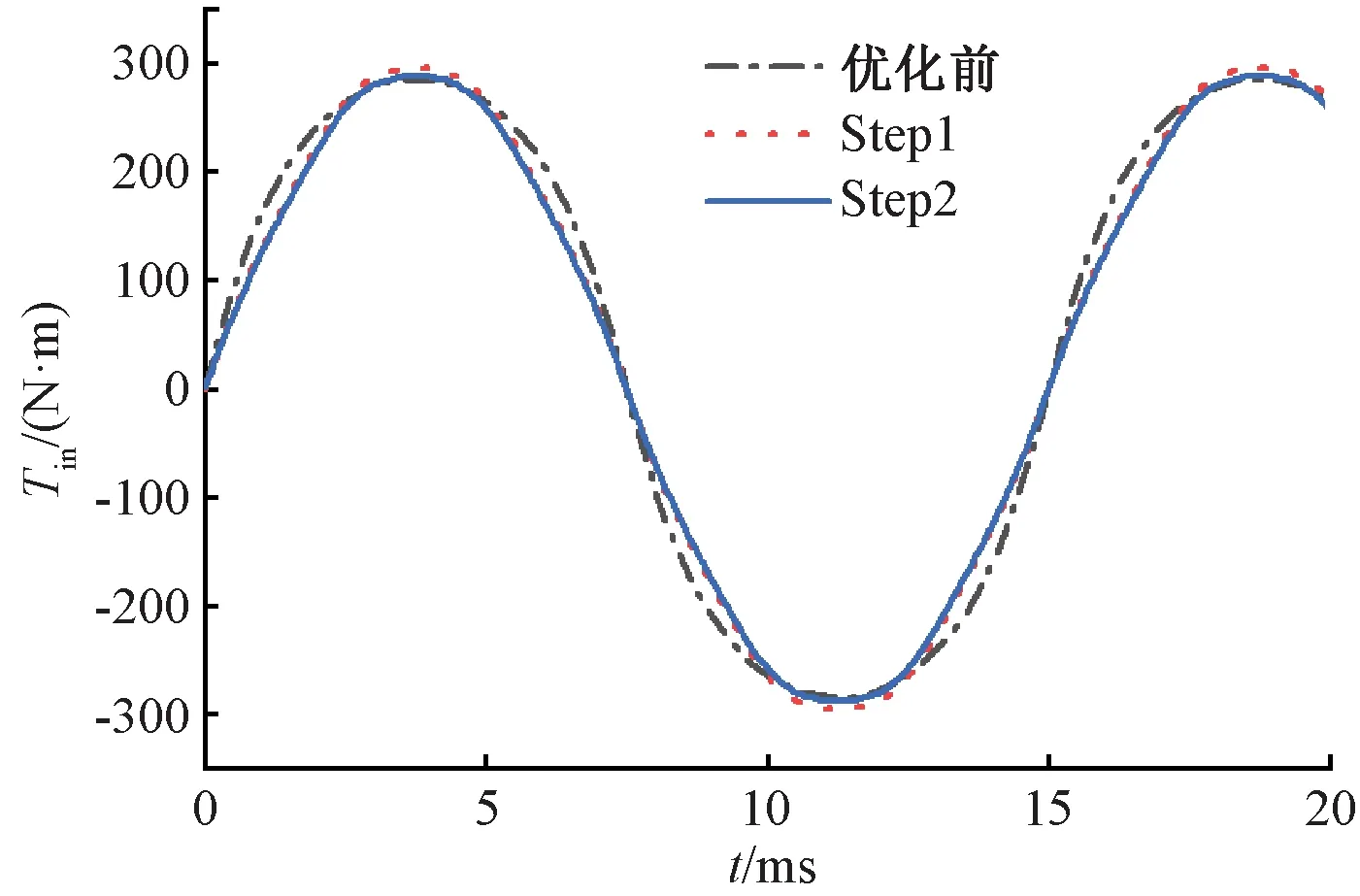
圖15 優化前后內轉子靜態轉矩對比

5 結 語

通過仿真實驗驗證與分析可以得出如下結論：

(1)采用三段式Halbach陣列可顯著提升同軸磁性聯軸器的轉矩密度，有效減少其總體積；

(2)以永磁體的轉矩密度以及同軸磁性聯軸器的體積為優化目標，合理選取優化變量，采用響應曲面法與模擬退火算法相結合的優化策略對復合性能函數進行求解，可起到提高空間利用率、節省永磁材料的目的，同時提高了實驗效率。