基于地震觀測數據的結構損傷水平表征參數研究

楊永強，楊耀鑫，楊 游，左占宣，公茂盛

（1.中國地震局工程力學研究所地震工程與工程振動重點實驗室，黑龍江哈爾濱 150080；2.地震災害防治應急管理部重點實驗室，黑龍江哈爾濱 150080；3.中國市政工程中南設計研究總院有限公司，湖北武漢 430010）

引言

根據地震發生后第一時間獲得的數據判斷結構損傷程度是實施應急救援行動關鍵依據，隨著現代傳感技術、信號采集與處理和信息融合技術的不斷發展，利用傳感器采集到的信息對結構的損傷進行識別的方法有了很大的進展。1995年阪神地震發生后，日本建筑研究所在日本主要城市的80棟典型建筑物上布設了密集強震動觀測儀器；我國從20世紀70年代起，陸續在一些重要結構如大壩和核電廠等布設了地震反應觀測臺陣，并陸續在中國地震局辦公樓、深圳地王大廈和上海中心等結構設立了地震反應觀測臺陣。因此如何利用我國現有并不斷建設的強震與烈度速報臺網、工程結構反應臺陣等收集到的數據，在震后快速評估結構損傷是地震工程領域面臨的重要挑戰之一。而結構在地震作用下動態參數如加速度、變形反應水平以及結構自振頻率變化等能提供結構的整體信息，結合合理的基于強震動觀測數據的工程結構損傷評估技術，震后快速對結構損傷程度進行識別是可行的。

使用結構動力響應參數來識別結構損傷程度已有眾多學者進行過研究，Cawley等［1］最先提出了通過測量結構自振頻率的改變來評估結構損傷狀態，實現了對二維平面結構損傷的檢測；Lam等［2］基于損傷特征匹配技術，利用結構振型的變化識別出二層鋼框架結構的損傷位置；Ren等［3］提出了一種基于結構自振頻率和振型變化的損傷識別技術，將受損后的特征值方程與結構受損模態相乘并求解方程，成功將此方法應用于梁的損傷識別上；Farrar等［4］將基于振動特性變化的損傷識別描述為一種統計模式識別，并提出了系統性的步驟運用在柱的損傷識別上；刁延松等［5］提出了基于AR模型和因子分析的損傷識別方法，利用加速度響應識別出4層鋼框架損傷發生的位置，實現了不利用有限元模型的情況下對結構進行實時監測；常軍等［6］利用橋梁的曲率模態結合隨機子空間方法，成功識別出橋梁的損傷程度。以上研究都證明了基于結構動力響應參數的損傷識別方法的可行性，但以上研究有以下2個不足之處：（1）大多數都只研究了單一參數與結構損傷之間的關系，并未對比不同參數與結構損傷之間相關性的強弱，且未考慮多個參數組合進行損傷預測；（2）大多數應用在簡單的梁柱構件或者桁架結構，只能給出結構構件的損傷相對程度，無法具體量化整體結構損傷程度，因此這些方法是否適用于整體RC框架結構有待進一步驗證。

針對現有研究的不足，文中根據9個數值算例的非線性時程分析所得結果，計算出最大層間位移角、結構自振頻率相對改變量和結構頂層加速度放大系數相關參數，并計算出結構整體的損傷指數以具體量化結構損失程度。采用數值擬合的方法研究了以上參數與結構損傷指數的相關性，并給出了它們擬合公式和擬合曲線。在此基礎上針對位移角數據獲取困難的問題，文中給出了一個組合結構體系參數，使用此組合參數在震后可以僅利用收集的結構加速度數據對整體結構進行快速地損傷評估，并且該組合結構體系參數與結構損傷指數的相關性優于組合前的單參數。

1 基礎數據

1.1 結構損傷指數與加權方法

結構損傷指數通過與結構損傷相關的參數計算得來，如變形、能量、強度或剛度退化等。用D來表示損傷指數，D為一個無量綱參數，D=0即結構未損傷，D≥1表示結構已完全破壞或倒塌，因此可以根據結構損傷指數的大小來判斷結構或構件的損傷程度。

由于使用單一參數對結構整體進行損傷評估會導致結果出現較大地誤差［7］，因此國內外學者根據歷次地震震后資料和實驗模擬提出了許多損傷模型，楊游等［8］對不同損傷模型進行了驗證及對比，表明Park-Ang模型對結構損傷的評估較為合理。因此文中選取Park等［9］提出的基于構件變形和耗能線性組合的損傷模型計算構件損傷指數，利用改進的杜修力加權方法加權得到結構總體損傷指數。

1.2 結構有限元模型

參考《混凝土結構設計規范》［10］設計了9個不同層數和設防烈度的RC框架結構，結構的立面圖如圖1所示，各層層高均為3.3 m，梁、柱的混凝土強度為C30，截面配筋的強度為HRB400，箍筋為HPB300，具體結構信息和配筋如表1所示，其場地類別為二類場地，設計地震分組為第2組。

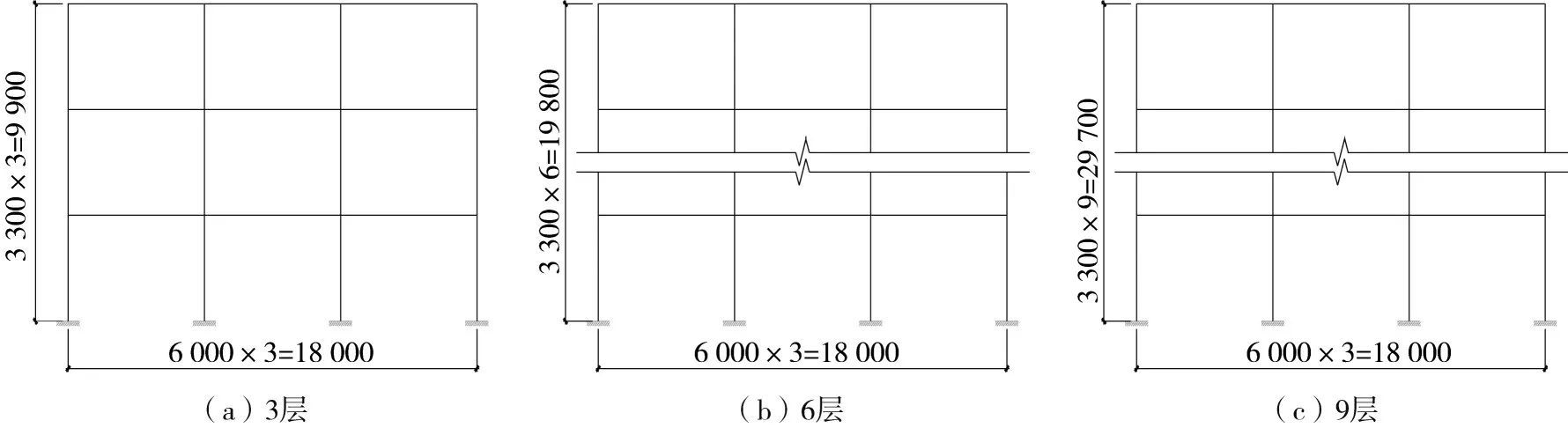
圖1 框架模型立面圖Fig.1 Elevations of frame structures（unit：mm）

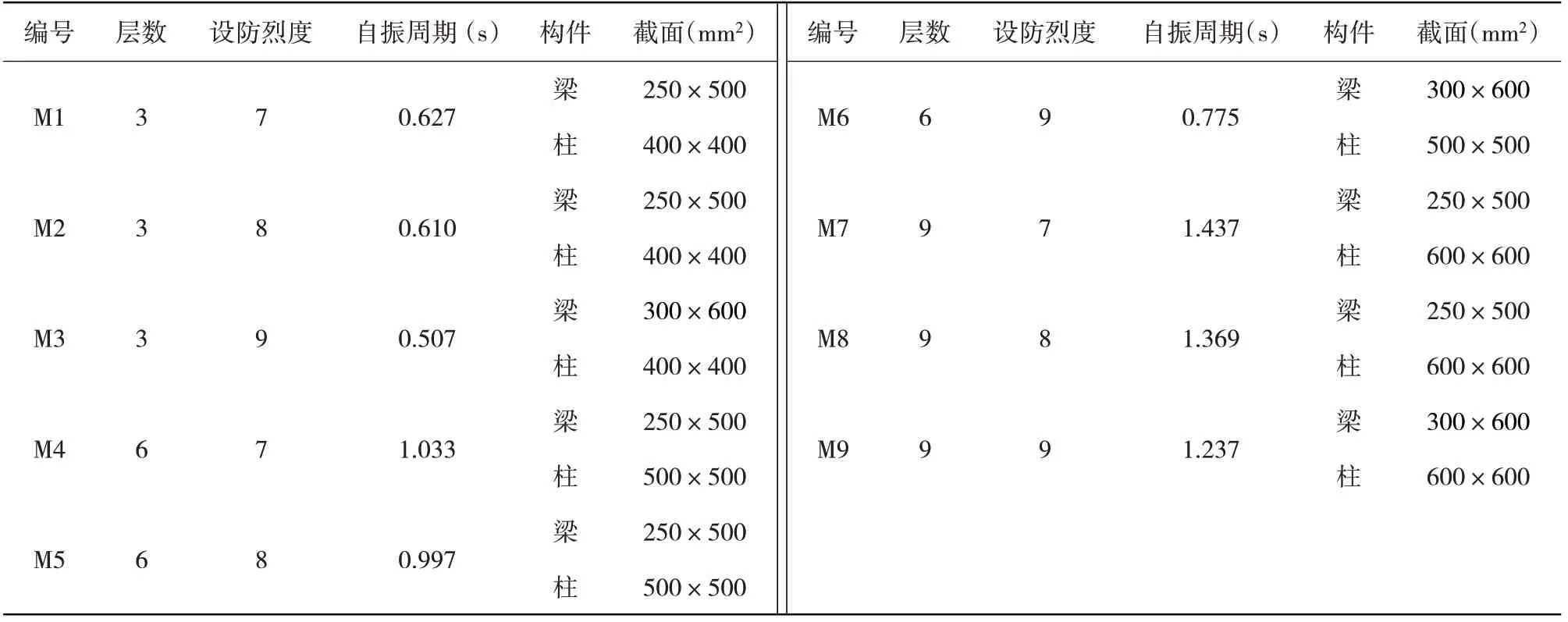
表1 有限元模型設計參數Table 1 Design information of finite element model

使用OpenSees［11］對9個結構的一榀框架建模，其中梁柱單元選用非線性梁柱單元nolinearBeamColumn單元，以在分析中考慮結構的P-Delta效應。柱、梁混凝土強度等級C30，混凝土的本構模型選用Concrete01材料，此材料是以單軸受壓本構模型為骨架曲線，且不考慮混凝土的抗拉強度。混凝土的峰值抗壓強度取20.1 MPa，峰值壓應變為0.001 64。鋼筋的本構模型選用Steel02材料，因其能較好地反映鋼筋的單軸各向同性的特征且考慮了Bauschinger效應。鋼筋的屈服強度取400 MPa，初始彈性模量取206 000 N/mm2，應變強化率取18。梁、柱構件的箍筋約束核心區混凝土的本構模型采用Mander箍筋約束混凝土的應力-應變關系模型［12］，用以計算約束后混凝土的峰值點和極限點處的應力和應變值，定義極限強度為4.02 MPa，極限應變為0.003 8。

1.3 有限元分析及數據的生成

基于郭鋒等［13］提出的方法，從PEER NGA-west2地震動數據庫挑選出對應于我國規范Ⅱ類場地條件地震動，并與《建筑抗震設計規范》［14］中的強震記錄選取方法進行二次篩選，選出100條符合條件的水平地震動。由于天然地震動中，能使結構造成嚴重破壞甚至倒塌的比例較低，大部分數據集中在結構無損傷和輕微損傷工況，不利于后續相關性的研究。因此調整地震動的PGA以使結構的破壞狀況相對均勻分布在無損傷至倒塌工況，此方法已經得到廣泛地認可［15］。利用OpenSees［11］有限元軟件，輸入調幅后的地震動，對上述9個框架結構進行非線性時程分析。并根據有限元計算所得的動力參數，采用1.1節方法計算出不同工況下的結構損傷指數。

2 結構損傷指數與單參數的關系

2.1 結構損傷指數與最大層間位移角的線性回歸

最大層間位移角通常被認為是判斷鋼筋混凝土結構在震后損傷程度的可靠指標，因為結構在地震作用下進入彈塑性狀態后，位移量的改變速度遠大于力的增長速度，使用基于位移的參數來識別結構的損傷程度是合理的［16］，最大層間位移角已經在許多研究中被用于評估結構的非彈性響應［17-19］，是目前用來判斷框架結構損傷程度應用最廣泛的指標。文中根據對9個結構有限元分析的結果發現結構損傷指數與最大層間位移角近似線性相關，因此提出擬合公式分別對9個結構的結構損傷指數和最大層間位移角進行線性擬合：

式中：D為結構損傷指數；θ為最大層間位移角；k1，k2為待定系數。計算得擬合系數見表2，擬合直線見圖2。

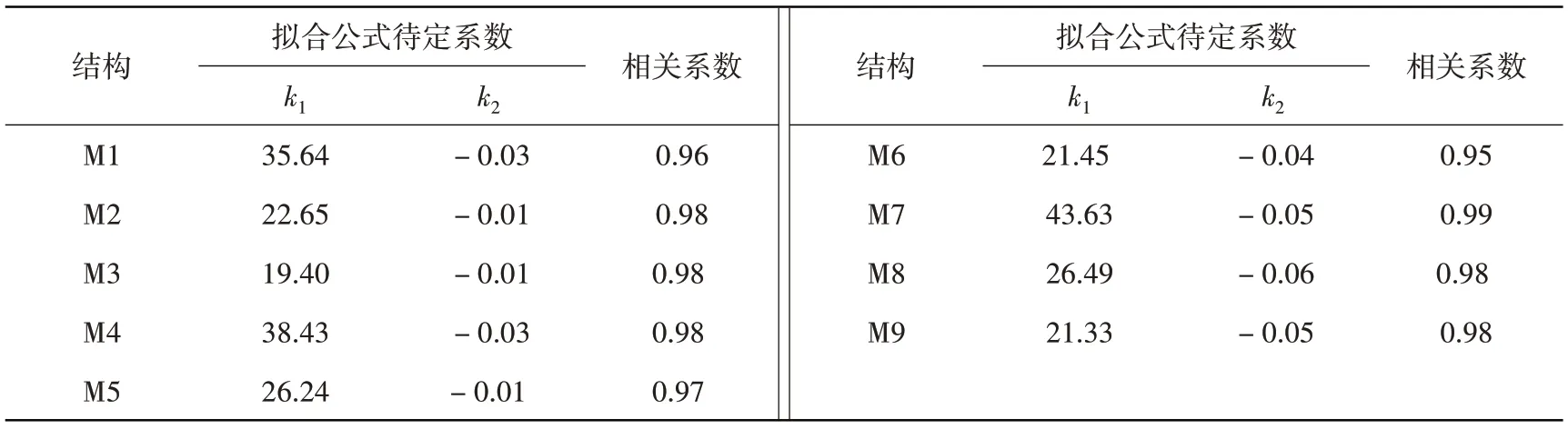
表2 結構損傷指數與結構最大層間位移角的擬合Table 2 The fitting of structural damage index and the maximum inter-story drift

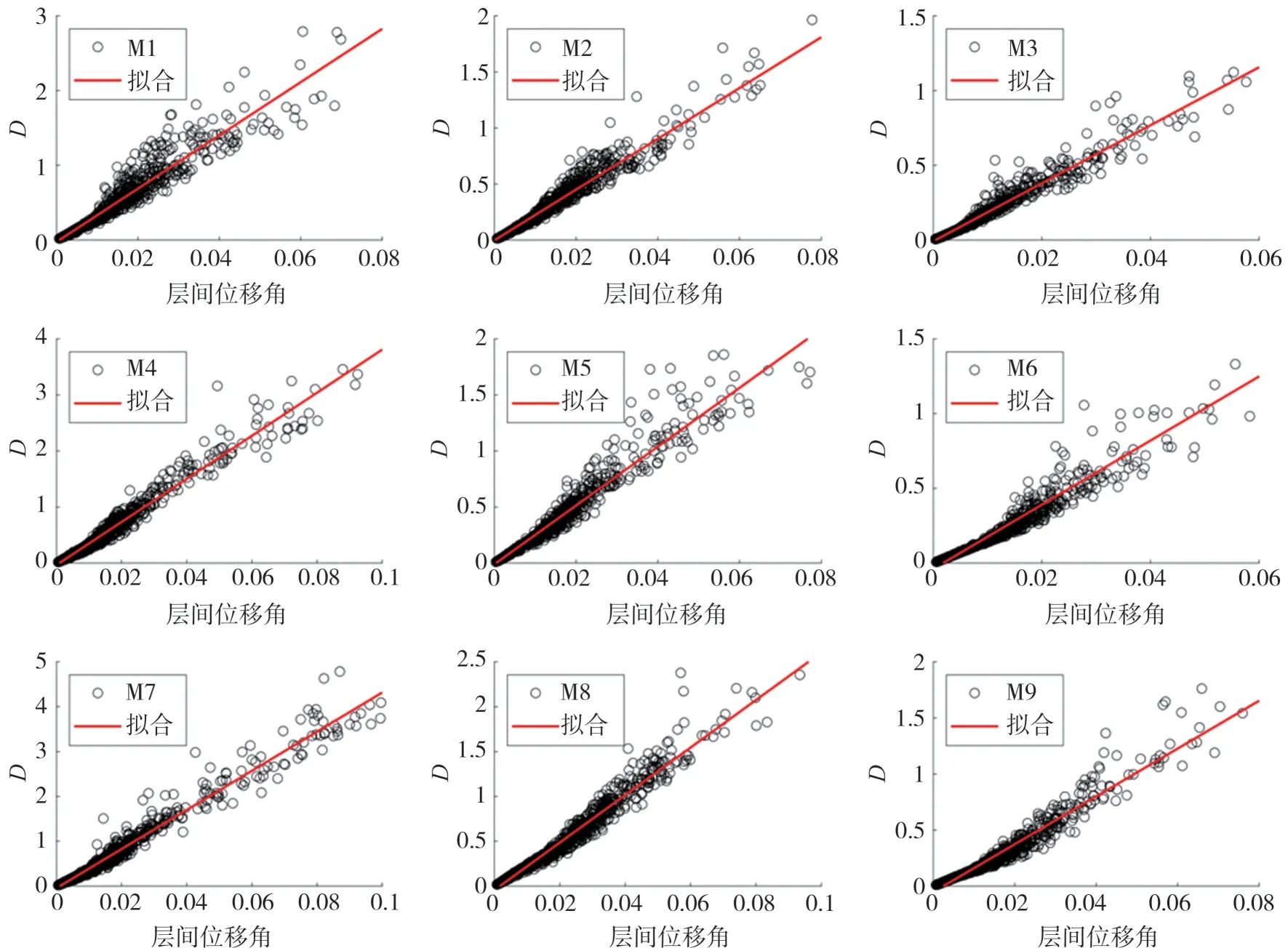
圖2 結構損傷指數與最大層間位移角的擬合圖Fig.2 Fitting diagram of structural damage index and the maximum interlayer displacement angle

文中采用Pearson相關系數r對擬合效果進行評價，Pearson相關系數變化范圍為[ -1,1]，r為正數時表示正相關，r為負數時表示負相關，汪東華［20］將Pearson相關系數劃分為極弱或不相關、低度相關、中度相關和高度相關4類，具體評價標準見表3。

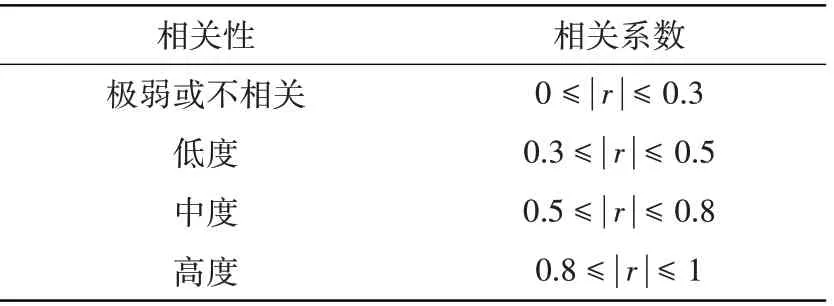
表3 相關系數的分類Table 3 Classification of correlation coefficients

從表2和圖2可以得出以下結論：（1）損傷指數和結構的最大層間位移角之間關系為正相關，并且9個結構得出的相關系數都表明結構損傷指數和最大層間位移角的相關性為高度相關；（2）從圖2可以看出離散點都分布在擬合直線附近，證明了最大層間位移角是識別結構損傷的良好指標。

2.2 結構損傷指數與結構頻率相對改變量的回歸

由2.1節分析可知結構最大層間位移角與結構損傷指數相關性較大，但在實際對結構監測過程中，獲得準確的結構層間位移數據比較困難，強震監測儀器獲取的加速度數據在實際工程中容易獲得且更為可靠［16］。結構損傷后一般情況下質量和剛度都會發生改變，自振頻率作為反映結構自身性質的敏感性指標，被廣泛地用于各種結構的健康監測。根據Salawu等［21］對使用頻率變化進行損傷識別的總結，頻率變化能較好地對反映結構整體損傷情況，因此考慮通過地震前后結構第一振型頻率變化來識別損傷。文中采用公茂盛等［22］提出的從結構頂層加速度數據識別結構自振頻率的方法，計算出結構震前后結構第一振型頻率變化，此方法經過驗證表明識別出結構的自振頻率與實驗獲得的自振頻率相比誤差很小，結果可靠。頻率相對改變量如式（2）所示，為歸一化的頻率參數，本節分析結構損傷指數與頻率相對改變量的關系。

式中：Δf為頻率相對改變量；f u為地震作用前的結構自振頻率；f d為地震作用后的結構自振頻率。

參考公茂盛［22］對結構損傷指數和結構體系參數的研究，提出一個三次多項式來擬合結構損傷指數和頻率相對改變量之間的關系：

式中，k1、k2、k3、k4為待定系數；其余同式（1）、式（2）。

計算出的M1-M9的待定系數和相關系數見表4，擬合曲線見圖3.

從表4和圖3中可以得出以下結論：（1）總體上看結構損傷指數與結構第一振型頻率相對改變量成正相關，相關系數中位值為0.60，基本可以認為二者中度相關。但在結構M3和M7上，離散點較多，相關性僅為低度相關；（2）從圖3可以看出頻率相對改變量在0～0.3之間時，點大多都在擬合曲線附近，但在其從0.3增加到0.5的過程中，離散點較多，擬合效果較差。綜上不建議單獨使用結構自振頻率相對改變量對結構損傷指數進行判斷，否則會導致較大的誤差。

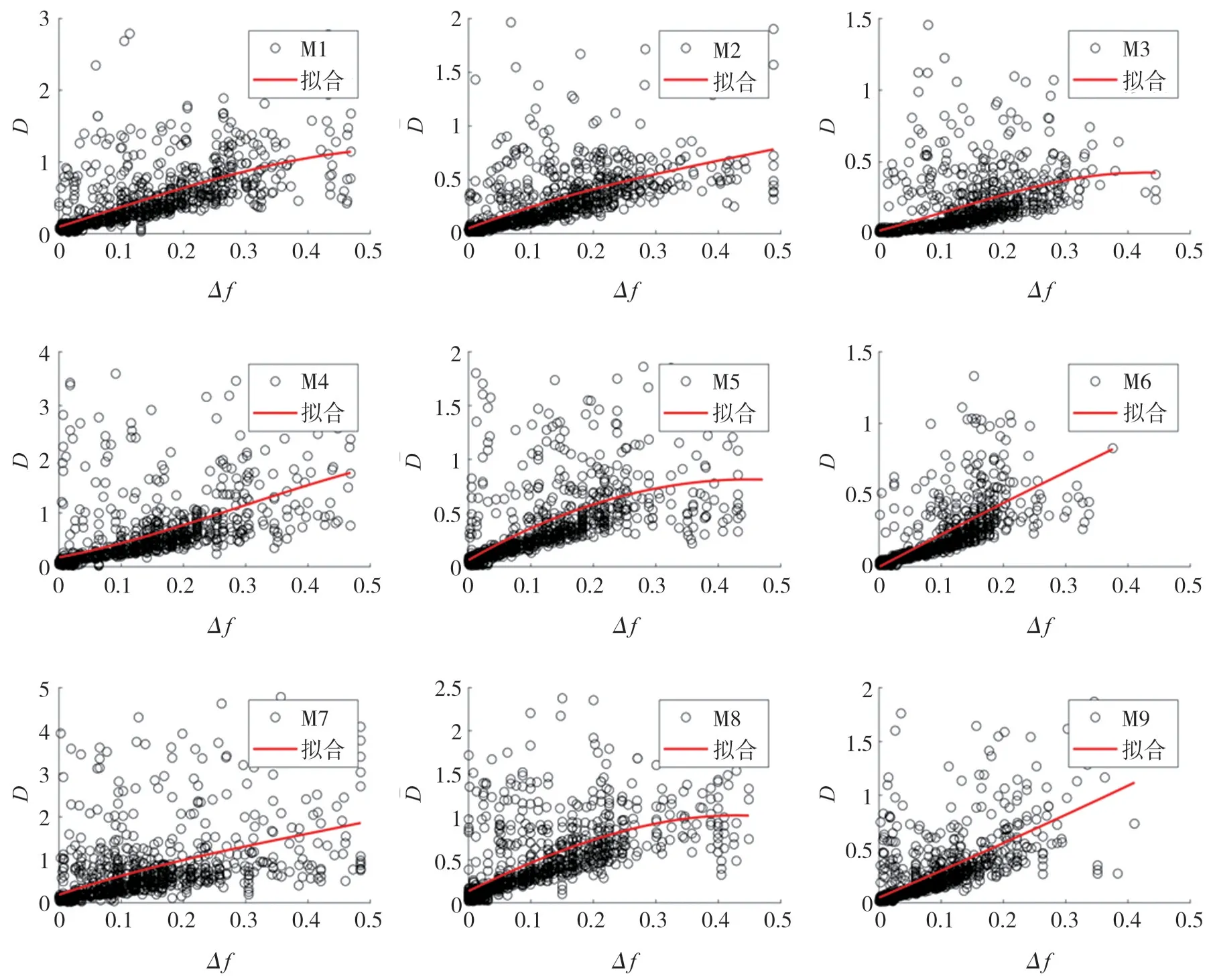
圖3 結構損傷指數與頻率相對改變量的擬合圖Fig.3 Fitting diagram of structural damage index and relative frequency change

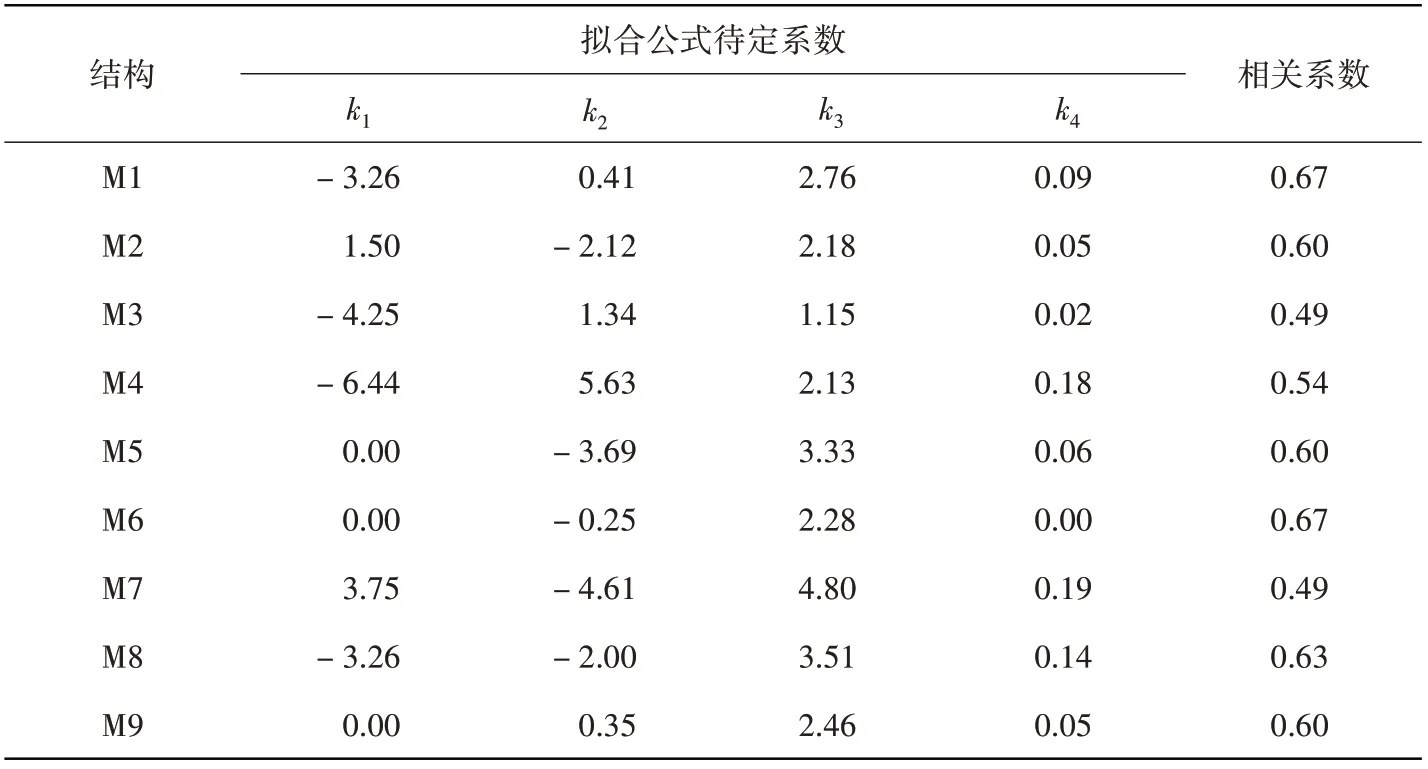
表4 結構損傷指數與頻率相對改變量的擬合Table 4 The fitting of structural damage index and relative frequency change

2.3 結構損傷指數與頂層加速度放大系數的回歸

式中，S為結構頂層加速度放大系數，其余同式（3）。計算得擬合系數見表5，擬合曲線見圖4。

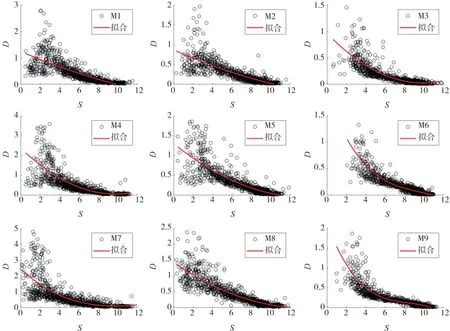
圖4 結構損傷指數與頂層加速度放大系數的擬合圖Fig.4 Fitting diagram of structural damage index and acceleration amplification coefficient of the top floor

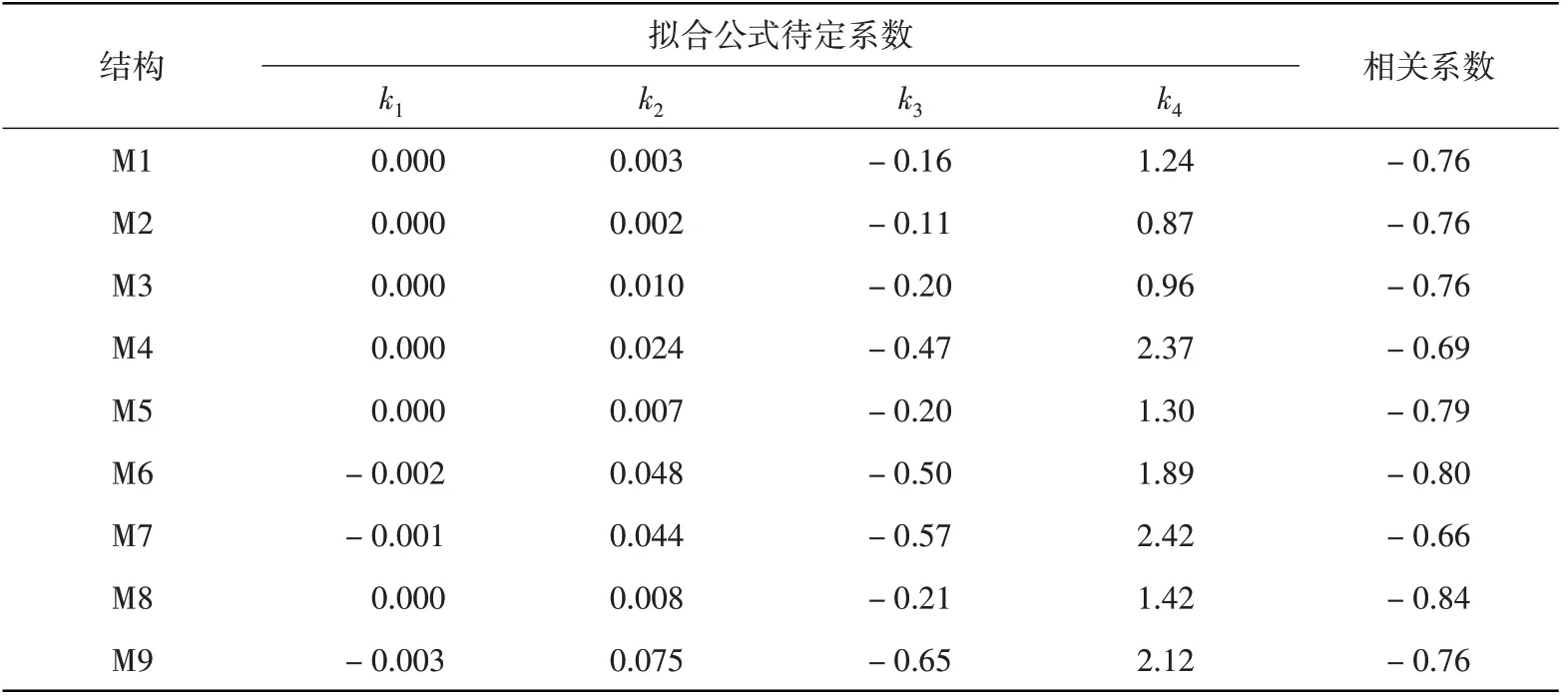
表5 結構損傷指數與頂層加速度放大系數的擬合Table 5 The fitting of structural damage index and acceleration amplification coefficient of the top floor

從表5和圖4中可以得出結論：（1）總體上看結構損傷指數與頂層加速度放大系數為負相關，相關系數的中位值為-0.76，因此相關性為中度相關；（2）頂層加速度放大系數在0到4之間存在較多離散點，但總體上看數據點基本分布在擬合曲線的周圍，且在結構損傷指數小于1時擬合效果良好。

3 組合結構體系參數

由以上分析可知，結構損傷指數和最大層間位移角的相關性為高度相關，而與頻率相對改變量和頂層加速度放大系數都為中度相關，且存在較多與擬合曲線偏離的離散點，因此單獨用頻率相對改變量或者頂層加速度放大系數去識別結構損傷指數效果并不理想。但是在實際監測中，如果使用布置大量位移計的方法來獲得最大層間位移角數據，需要耗費大量的金錢和人力［24］，且不能方便地重復使用［25］；如使用加速度數據積分來推導位移數據，受到傳感器噪聲和邊界條件的限制，結果并不精確［26］。而使用加速度傳感器獲得的加速度數據更易獲得且更準確［27］，此外隨著智能手機的普及，公眾收集到的加速度數據在震后損傷識別中也能發揮更加積極的作用［28］。值得一提的是，文中的頻率相對改變量和頂層加速度放大系數都為使用頂層加速度數據推導而來，因此在實際工程比最大層間位移角更易獲得。

基于此原因文中提出組合結構參數x，x由頻率相對改變量和頂層加速度放大系數組成，嘗試使組合結構體系參數x與結構損傷指數的相關性比單參數更好。通過相關性分析及多次試算，提出如下的組合結構體系參數：

式中：x為組合結構參數；Δf為結構自振頻率相對改變量；S為結構頂層加速度放大系數；k1、k2、k3為待定系數。

同樣采用三次多項式擬合結構損傷指數和組合結構參數x之間的關系，擬合公式如下：

式中：D為結構損傷指數；x為組合結構體系參數；a1、a2、a3、a4為待定系數。組合公式待定系數、擬合公式待定系數及相關性系數見表6，擬合曲線見圖5。

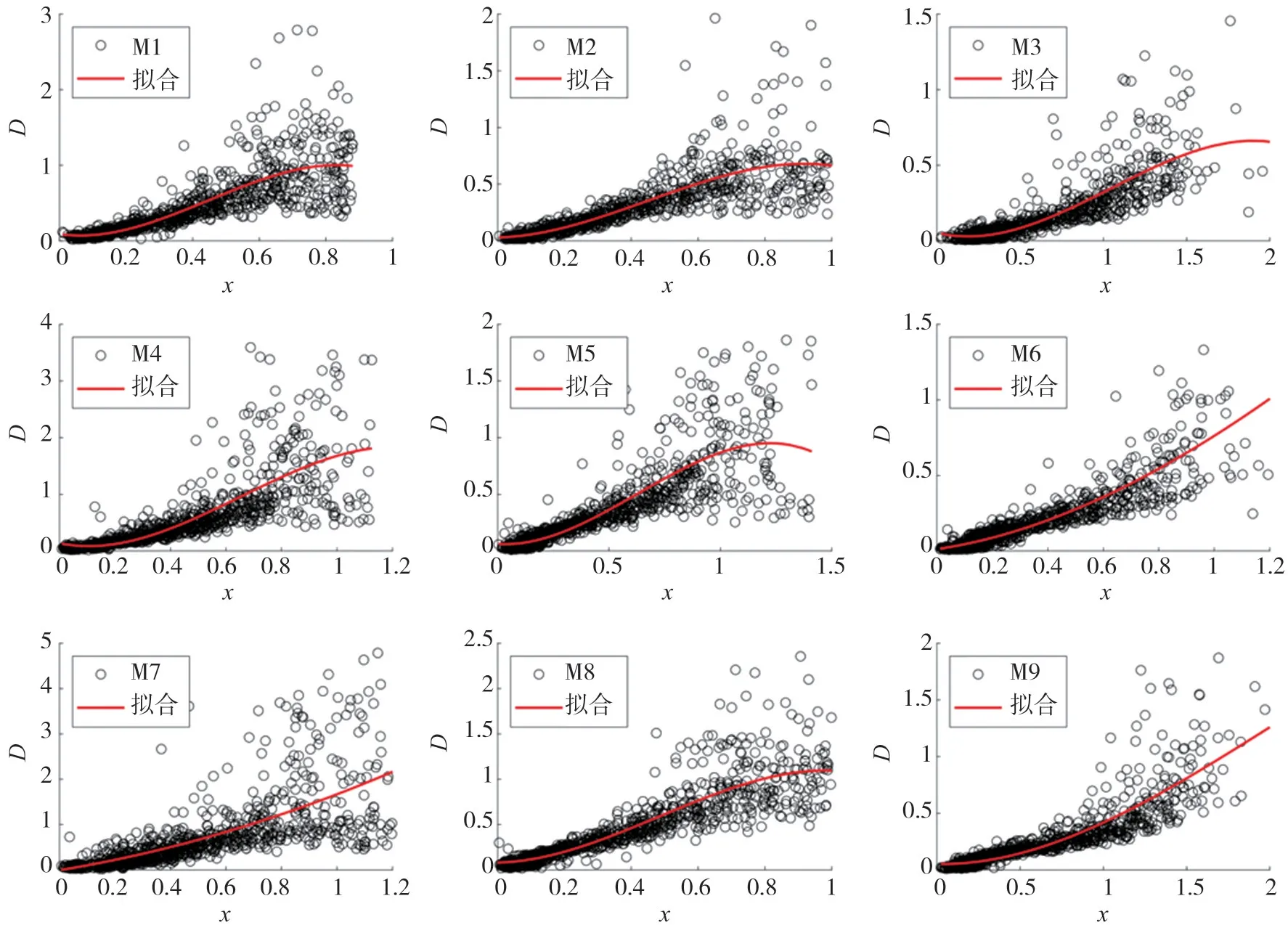
圖5 結構損傷指數與組合參數的擬合曲線Fig.5 Fitting diagram of structural damage index and combination parameters

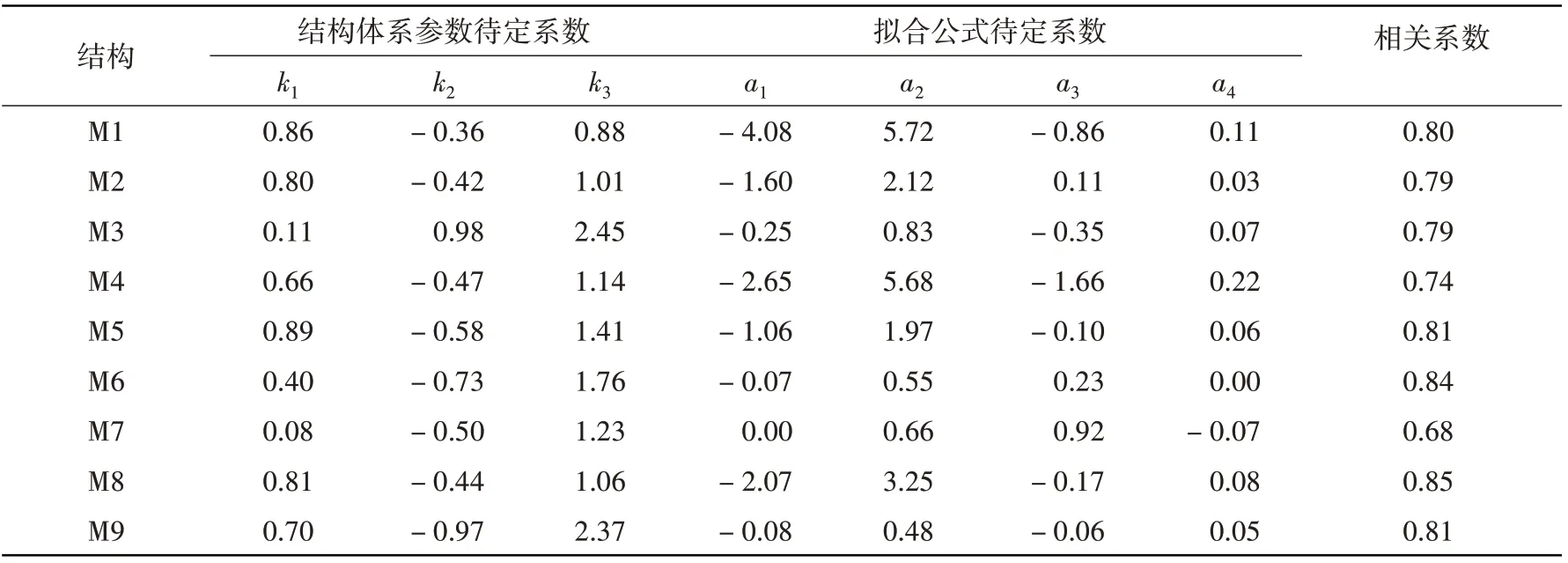
表6 結構損傷指數與組合參數的擬合Table 6 The fitting of structural damage index and combination parameters

同時為了更好地比較組合結構參數和單獨參數的擬合效果，引入均方誤差函數MSE（mean squared error，MSE）：MSE=。式中，N為樣本總量，y i為擬合值，x i為真實值，‖·‖為2-范數，即為預測值與真實值之間的距離。組合結構體系參數的相關系數和單參數的對比見表7，均方誤差的對比見表8。

表7 不同參數的相關系數對比Table 7 Comparison of correlation coefficients of different parameters

表8 不同參數的均方誤差函數對比Table 8 Comparison of mean squared error of different parameters

從表6、表7、表8和圖5可以得出以下結論：

（1）結構損傷指數與組合結構體系參數成正相關，9個結構相關系數的中位數為0.80，可以認為組合結構參數與結構損傷指數高度相關；

（2）從表7和表8可以看出，提出的組合結構參數與結構損傷指數的相關性在9個結構上都要優于單參數，9個結構單獨的均方差和平均均方差也小于單參數。說明相比頻率相對改變量和頂層加速度放大系數，組合結構參數與結構損傷指數的相關性更好，擬合值的方差更小；

（3）從圖5點的分布可以看出在結構損傷指數在［0，1］時相關性較強，在此范圍內除了極少部分離散點外大部分點都靠近在擬合曲線上。在破壞程度更大時，即結構損傷指數大于1時，點的離散程度顯著增加，說明式（6）的擬合精度下降，然而此時結構的破壞程度已處于倒塌狀態，在這種情況下識別的結構損傷指數的精度不重要［18］，能判斷出結構處于倒塌狀態已經能滿足震后損傷快速評估的要求。

4 結論

文中設計了9個鋼筋混凝土框架結構，并分析了結構在地震作用后的損傷指數與結構在地震作用下動力響應參數之間的相關性，對結構損傷指數與結構最大層間位移角、頻率相對改變量和結構頂層加速度放大系數的關系進行了回歸分析。由于目前在地震作用下準確地獲得結構的位移數據需要布置大量的位移傳感器，且維護困難需要耗費大量的人力及物力，使用最大層間位移角來識別結構的損傷程度在某些情況下具有局限性。因此基于結構頻率相對改變量和結構頂層加速度放大系數提出了一個組合結構體系參數，建立了一個組合結構體系參數與結構損傷水平的關聯模型。文中主要得出以下結論：

（1）結構損傷指數與最大層間位移角高度正相關，最大層間位移角是識別結構損傷的良好指標，如果在震后能獲得準確的最大層間位移角數據即可較好地用于預測結構震后損傷程度。

（2）結構自振頻率相對改變量與結構損傷指數正相關，結構頂層加速度放大系數與結構損傷指數負相關，通過相關性分析，可以認為二者都為中度相關，因此不建議單獨使用結構自振頻率相對改變量或者結構頂層加速度放大系數對結構整體損傷程度進行識別。

（3）文中提出了一種基于頻率相對改變量和頂層加速度放大系數的組合結構體系參數，與結構損傷指數高度相關，相關性和誤差均優于組合前的單參數。且計算所需要的加速度數據在實際工程中易于獲得，可用于在震后對平面布局規則的非高層框架結構損傷進行快速評估。

文中以RC框架結構研究對象，探討了結構損傷指數與最大層間位移角、自振頻率相對改變量和頂層加速度放大系數之間的相關性，并以結構自振頻率相對改變量與頂層加速度放大系數來建立組合結構參數，未來可針對多種結構類別及更多的結構動力參數，進行更全面地研究。