基于地磁方向熵的高空地磁匹配航跡選取方法

鄧小波，趙軍瑞，宋 勝

(1.中國人民解放軍61711部隊，新疆 喀什 844000；2.中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

0 引言

地磁場是地球本身固有的基本物理場[1]。在主地磁場基礎上，不同位置的地形和組成物質不同，導致局部的異常場[2-4]，而且異常場與空間地理位置存在一定的對應關系。基于異常場匹配的地磁匹配導航是一種無源、自主的導航方式，具有良好的應用前景[5-8]。

在地磁導航算法的研究中，穆華等人[9]采用了擴展卡爾曼濾波的方法研究了慣性/地磁組合導航技術在船舶導航方面的應用，仿真結果證明慣性/地磁導航魯棒性好，可實現長航時工作；楊功流等[10]研究了基于Sigma點采樣的UKF方法構建慣性/地磁卡爾曼濾波器，相比于使用EKF方法避免了非線性系統的線性化誤差；朱占龍等[11]研究了使用新息正交法的自適應濾波方法，仿真結果證明該方法提高了組合導航系統對野值的適應能力，提高了系統的可靠性；劉睿[12]研究了慣性/地磁/天文的組合導航方法，綜合了多種導航方式的優點，構造了長航時高精度的組合導航系統。上述研究主要針對地面、水下以及低空域進行地磁匹配算法研究，然而高空高速飛行器由于地磁場環境和運動特性有所不同，需要對其導航方法進行針對性研究。

地磁圖的準確性和包含可用信息量的大小是影響地磁匹配導航精度的重要因素。而不同位置地磁異常場特性不同，能用于匹配導航的信息量也不同。因此，進行地磁匹配導航前需要選擇適合匹配的區域[13-16]。同時，穿越地磁區域的航跡方向也會影響到地磁匹配的效果，這也是進行載體航跡規劃的重要依據[17-18]。

本文根據對高空地磁圖特性的分析，利用高空大范圍地磁梯度呈現趨勢性的特點，提出了地磁方向熵的概念，由此給出了一種高空高速飛行器的地磁匹配軌跡選取方法。

1 高空地磁圖匹配的特性分析

目前，高空地磁異常場測量在實現上面臨較大困難，通常通過采集地面或低空地磁異常場數據，然后通過延拓方法得到高空地磁場的方案[19]。這使得高空地磁異常場的特性與地面或低空地磁異常場有所不同[20]。取1 000 m高度地磁圖和30 000 m高度地磁圖繪制三維曲面圖，如圖1所示。

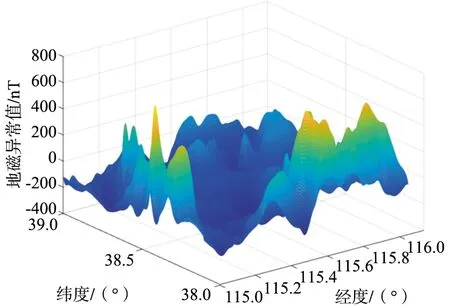
(a) 1 000 m

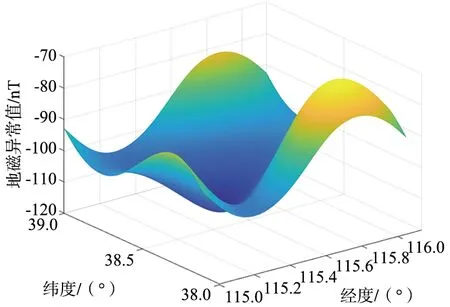
(b) 30 000 m圖1 同一區域不同高度的地磁場三維曲面圖Fig.1 3D surface map of the geomagnetic field at different altitudes in the same area

通過對比圖1不同高度的地磁三維圖可以看出，高空地磁異常場的變化相比低空更加平滑。因此，高空地磁匹配算法需要適應高空地磁圖的特點。地磁異常場的削弱意味著對地磁傳感器測量精度的要求比地面地磁匹配要高。而高空地磁場這種平滑有明顯趨勢性變化的特性也會對地磁匹配方法提出新的要求和需要解決的問題，即飛行器飛入方向和飛行軌跡問題。高空地磁異常圖的波動較小，起伏變化具有明顯的與地理位置有關的趨勢性，這使得飛行軌跡的航向和等值線變化趨勢的角度會影響到匹配的性能。飛行軌跡與地磁等值線處于近平行狀態時，匹配性能較好，而處于近垂直狀態時匹配誤差增大，且匹配概率大大降低。基于以上技術背景，提出地了磁梯度網絡和地磁方向熵結合的地磁匹配航跡選擇方法。

2 數字地磁圖的地磁梯度向量場

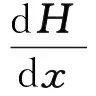
然而，實測的地磁圖一般都是離散的，以二維數組的形式存儲在計算機中。二維數組可以以更加簡單的方式計算地磁梯度，即使用地磁矩陣的數值梯度(Numerical Gradient)來計算數字地磁圖沿著x方向和y方向的地磁場梯度。

矩陣的數值梯度的定義為二維函數在x方向和y方向的偏導，其值為：

(1)

對于矩陣這種離散數據，可以通過計算差分的方式來取代求偏導。例如對于單位間距的矩陣A，其內部的數據可以采用中心差分的方式計算梯度。內部梯度值G(:,j)為：

G(:,j)=0.5×(A(:,j+1)-A(:,j-1))，

(2)

式中，j∈(2～N-1)，對于矩陣邊緣的數據，可以采用單邊差分的方法計算梯度：

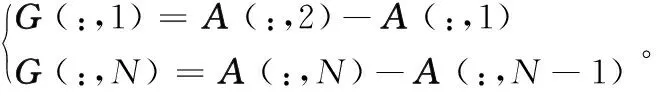
(3)

通過差分計算的方法可以得到離散的數字地磁矩陣關于x方向和y方向的梯度分量。其向量和為當前位置的地磁梯度向量，該向量的方向即為地磁場強度增大的方向。該向量的角度可利用x梯度與y梯度按照四象限反正切的方法計算出來：

(4)

式中，Y和X表示地磁場y方向和x方向地磁場梯度值;θ表示該向量按照北偏東為正方向的角度。將地磁梯度向量以箭頭的形式，在地磁圖內繪制出來，就稱為向量場地磁圖，或向量網格地磁圖。以高空30 000 m地磁圖的一個區域為例，其梯度向量場地磁圖如圖2所示，向量場地磁圖中的網格數為100×100，橫縱坐標分別表示網格的序號。因較為密集，圖中給出了部分區域的放大。

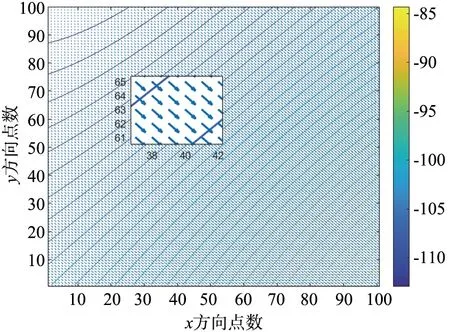
圖2 高空30 000 m區域的梯度向量場地磁圖Fig.2 Gradient vector magnetic field map at 30 000 m altitude

可以看出，向量場中的向量箭頭指向的是地磁場強度增大的反向，即由深藍色等值線變化到黃色等值線，與右側色標相對應。通過將式(1)中的四象限反正切公式改為：

(5)

由此畫出的地磁梯度網格如圖3所示。

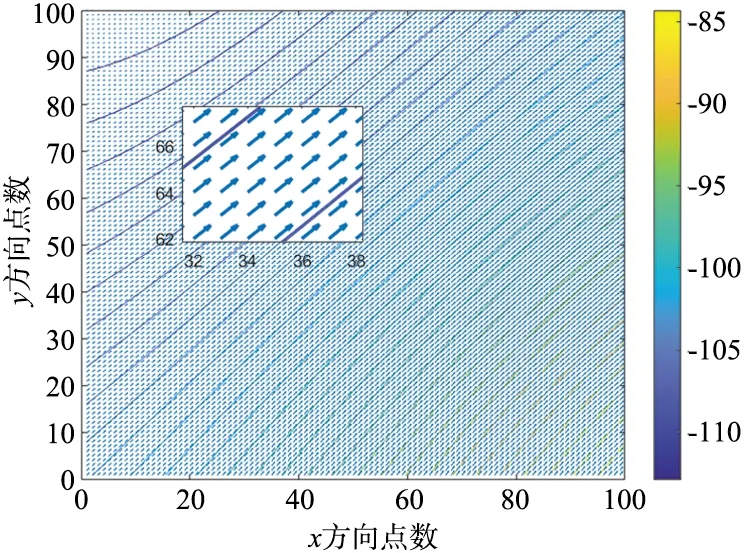
圖3 高空30 000 m區域的平行等值線向量場地磁圖Fig.3 Parallel isoline vector magnetic field map at 30 000 m altitude

相比式(4)，式(5)求解出的θ結果相當于逆時針旋轉90°，變為與地磁場強度梯度垂直、與地磁等值線平行的曲線；同樣，可以從圖3放大部分看出，由式(5)繪制出的向量場地磁圖中的箭頭與等值線方向平行。

隨著高空地磁場隨高度衰減，地磁等值線的變化趨勢也逐漸趨于平緩。換言之，地磁場等值線就是高空地磁圖中逐漸在大范圍內趨于平行的直線。高空30 000 m的最大地磁信息熵區塊中地磁圖區塊的地磁圖等值線就符合這種特性，整個圖內的等值線幾乎都沿著一個方向呈現平行分布的趨勢。因此，在該地磁區域內，地磁匹配方法應當適應這種特性。常用的MSD方法在航跡與等值線呈現過大角度，例如接近垂直于等值線時，平行于等值線方向的軌跡的慣導誤差較大，但這些誤差無法通過MSD方法匹配到真實位置附近，地磁匹配幾乎失效。而當航跡平行于等值線方向時，慣導誤差就能通過MSD方法匹配到，匹配的精度就能大大提高。

3 地磁方向熵

向量場地磁圖表現了地磁數據中每個位置地磁場等值線的方向情況。實際上，為了衡量一個地磁圖區域內整體性的地磁場等值線的復雜程度，可以構建出地磁方向熵的概念，其公式為：

(6)

該式的物理意義為：通過式(4)和式(5)可以計算出向量場中每個地磁梯度或等值線平行矢量的方向(該方向以北為起點，北偏東順時針為正，范圍為-180°～180°)。將這些矢量的角度排序后成為矢量角度數據集，將-180°～180°的范圍劃分為K個等跨度區間。矢量角度數據集落在對應K個等跨度區間內，每個區間的數量為ni。按照式(6)計算得出的Hdir就是對應地磁場區域的地磁方向熵。

從地磁方向熵的物理意義來看，地磁方向熵反映出地磁場內等值線的變化復雜程度。地磁方向熵越小，地磁矢量角的分布越集中，這意味著該區域內的地磁場等值線在大范圍內呈現出平行直線的形狀，其角度方向統一。地磁方向熵越大，說明地磁場等值線在大范圍內呈現出較為豐富的形狀變化，或大范圍內地磁等值線形成閉環。對高空地磁圖來說，其本身伴隨著地磁等值線峰值的削弱，地磁等值線越平直，越適合降低地磁匹配算法的匹配誤差。

4 仿真與分析

仿真實驗在圖2所示的地磁區域內進行。通過地磁方向熵計算方法，將地磁區域內的所有地磁矢量角劃分為36個等跨度區間，計算得到地磁方向熵值為0.126 6。這個值意味著地磁等值線中的地磁矢量角高度集中于跨度區間[40°，50°]，即和等值線近似平行的角度。根據預測，航向角屬于該區間內的軌跡的匹配效果更好。為了證明這個預測結果，設計3條航跡，分別為平行等值線、呈45°和垂直等值線來驗證仿真結果。根據地磁方向上設定3條運動軌跡的飛入點都在(38.39°N,115.45°E)，飛行速度為3 400 m/s。地磁等值線的方向大約為北偏東45°，本文選擇的3條運動軌跡由飛入點進入后的飛行方向與地磁等值線間的初始夾角分別選為：航跡① 0°(近平行狀態)、航跡② 45°(中間狀態)和航跡③ 90°(近垂直狀態)；對應的航向分別為：航跡① 北偏東50°、航跡② 北偏東90°和航跡③ 北偏東130°。3條運動軌跡如圖4所示。

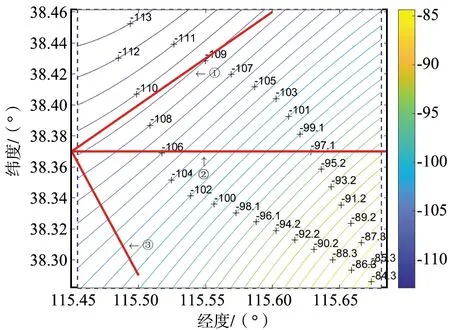
圖4 3條預設仿真軌跡Fig.4 Three preset simulation tracks

與3條運動軌跡相對應，設定的慣導系統初始誤差、慣性器件誤差和地磁誤差如表1所示。

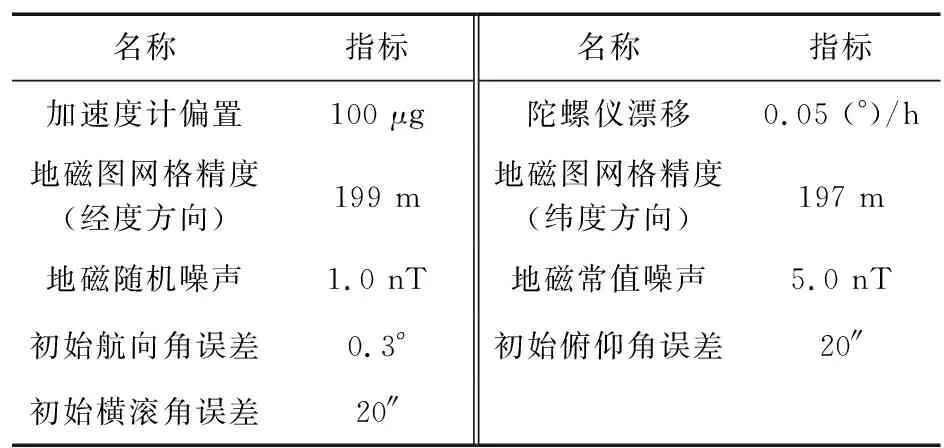
表1 仿真誤差設置Tab.1 Simulation error setting

飛行器的仿真導航算法采用慣性/地磁匹配松組合，將MSD法計算得到的匹配位置輸入松組合卡爾曼濾波器，用以修正慣導軌跡。

飛行器分別按照以上3條運動軌跡運動，運動過程中匹配定位結果分別如圖5、圖6和圖7所示。

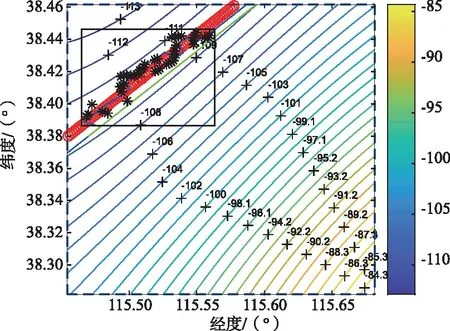
(a) 原始大小

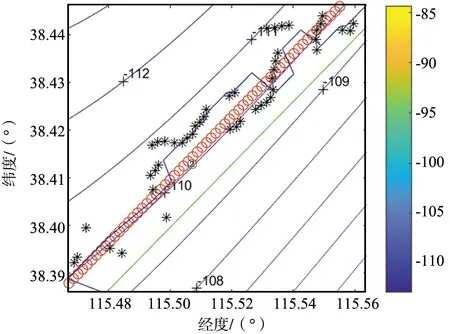
(b) 部分放大圖5 軌跡1的匹配效果圖Fig.5 Matching result of track 1

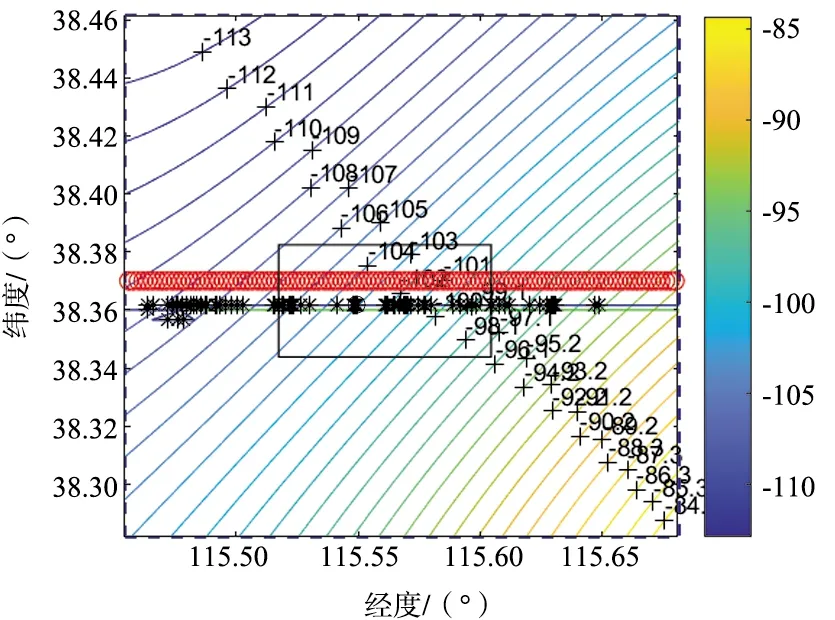
(a) 原始大小

(b) 部分放大

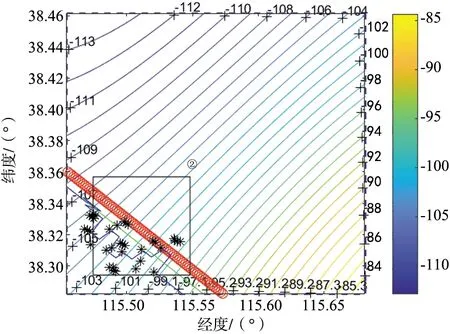
(a) 原始大小

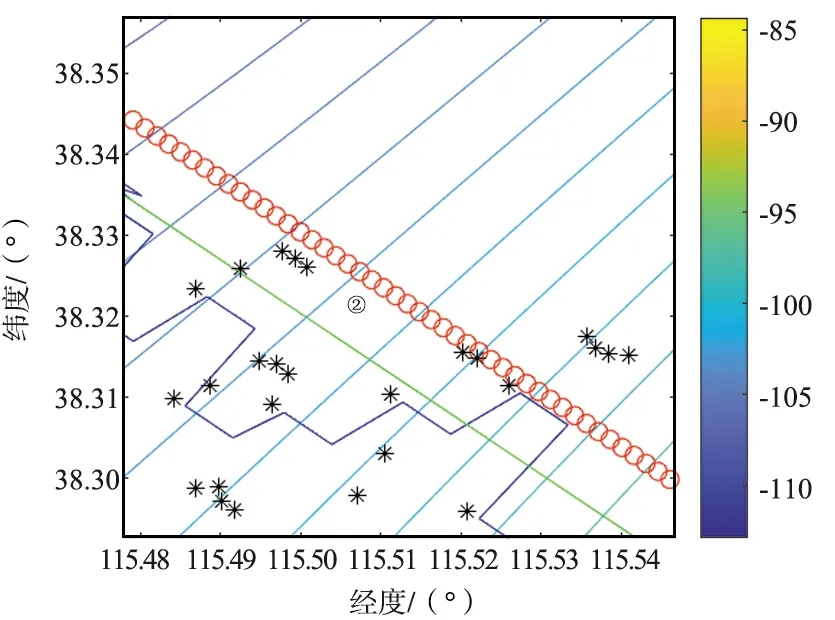
(b) 部分放大

圖5、圖6和圖7的(a)圖為匹配區域內的航跡的匹配定位圖，(b)圖為相應3幅圖中黑色細實線框內小段軌跡的放大示意圖。各幅圖中，紅色圓圈為軌跡真值位置，綠色實線為純慣導輸出位置，黑色星號點為地磁匹配定位結果，藍色細實線為地磁匹配算法校正慣性導航后輸出的軌跡。

圖5中，軌跡①匹配效果良好，定位結果基本和真值重疊，匹配誤差為530.19m(1σ)。軌跡②匹配結果接近真實位置，但其定位誤差較大，匹配誤差為2 051.11m(1σ)。軌跡③地磁匹配定位結果逐漸偏離真值，呈發散趨勢，仿真中匹配定位誤差達到4 162.34m(1σ)。

5 結束語

針對高空地磁圖等值線呈現趨勢性和全局隨機性下降的現象，本文結合地磁信息熵與地磁方向熵2種量化指標，研究了高空地磁匹配區域飛行航跡選取方法。由仿真可見，在軌跡與等值線呈近平行狀態時，其匹配定位誤差較小，隨著運動軌跡與等值線夾角增加，匹配定位誤差加大，且在近垂直狀態時其匹配結果可信度很差。數據處理結果說明了應用地磁方向熵選擇飛行軌跡方向對提高地磁匹配定位精度具有重要作用和效果。