頻散介質(zhì)中的瞬變電磁響應特征和反演特性分析

智慶全， 武軍杰， 王興春， 楊 毅，張 杰，鄧曉紅

(1.中國地質(zhì)科學院 地球物理地球化學勘查研究所，廊坊 065000;3.國家現(xiàn)代地質(zhì)勘查工程技術研究中心，廊坊 065000;4.長安大學 地質(zhì)工程與測繪學院，西安 710054)

0 引言

瞬變電磁法(TEM)因其體積效應小、分辨力高、對良導體敏感的優(yōu)勢，在金屬礦產(chǎn)勘查、地質(zhì)調(diào)查等領域得到了廣泛的應用[1-3]。由于極化介質(zhì)的廣泛存在，大地固有頻散特性，電磁場在地層中傳播會產(chǎn)生頻散效應，引起低頻的激發(fā)極化(IP)效應和高頻的介電極化[4]。在瞬變電磁法常見的工作條件下，介電極化效應較弱而難以體現(xiàn)，因而TEM響應中的頻散效應一般為激發(fā)極化效應，其響應疊加在瞬變電磁響應之中。當?shù)叵麓嬖跇O化地質(zhì)體時，會產(chǎn)生較強的IP效應，導致瞬變電磁響應的畸變，破壞瞬變電磁響應隨大地電性變化的正常衰減規(guī)律，甚至出現(xiàn)響應符號反轉(zhuǎn)現(xiàn)象，給瞬變電磁數(shù)據(jù)處理帶來了困難和干擾，以至于造成錯誤解釋。研究和分析頻散介質(zhì)中的瞬變電磁響應特征及其反演特性，是瞬變電磁數(shù)據(jù)處理問題的關鍵和前提。

頻散介質(zhì)中瞬變電磁響應的畸變現(xiàn)象很早就引起了地球物理學者的注意，并引發(fā)了一系列有價值的討論和分析。Spies[5]最先報道了澳大利亞礦產(chǎn)資源地質(zhì)和地球物理局自1972年以來多次觀測到的重疊回線裝置的TEM響應符號反轉(zhuǎn)現(xiàn)象，分析了造成這種現(xiàn)象的原因可能有磁性效應、電磁波的反射以及復電導率效應(包含位移電流和IP效應)等幾種，并指出其中最為合理的解釋是IP效應；Weidelt[6]從理論上證明，對于無頻散介質(zhì)中的重疊回線TEM響應，由于其積分核函數(shù)的嚴格非負性，任意的電導率和磁導率都不會導致其符號反轉(zhuǎn)，從而確定了造成瞬變電磁響應符號反轉(zhuǎn)的主要原因是頻散介質(zhì)的IP效應；Smith等[7]使用兩個相互作用的阻抗環(huán)模擬了頻散介質(zhì)中瞬變電磁響應符號反轉(zhuǎn)現(xiàn)象出現(xiàn)的過程，從物理上解釋了頻散介質(zhì)中符號反轉(zhuǎn)現(xiàn)象的產(chǎn)生機理。

在頻散介質(zhì)中瞬變電磁響應的定量分析方面，Pelton等[8]首先通過對大量巖礦石標本和露頭的測量，證明了描述電極化的Cole-Cole模型同樣適用于描述激發(fā)極化效應[9]，奠定了極化介質(zhì)中瞬變電磁響應定量計算的理論基礎；Lee[10]采用Cole-Cole模型推導了頻散均勻半空間的瞬變電磁響應，利用級數(shù)展開給出了漸進表達式，證明了在頻散地層中的IP效應會導致瞬變電磁響應的符號反轉(zhuǎn)；Raiche[11-12]利用基于G-S變換的層狀大地正演算法對Lee的結果進行了驗證，取得了相一致的結果；Flis等[13]計算了含頻散效應的一維地層和三維體瞬變電磁響應，系統(tǒng)分析了頻散地層和頻散體參數(shù)對TEM響應的影響，提出大地的頻散效應可以分為充電和放電兩個階段，并嘗試進行了含IP效應TEM數(shù)據(jù)的定量解釋；殷長春等[14]利用積分方程法計算了兩層大地中三維異常體的TEM響應，分析了影響三維極化體響應的因素；孫鴻雁[15]和王隆平等[16]分別通過理論分析和物理模擬研究了頻散大地上極化體和觀測參數(shù)對磁性源瞬變電磁響應的影響特征，討論了通過指數(shù)函數(shù)擬合分離IP效應和增加發(fā)射磁矩、移動發(fā)射框位置等辦法削弱IP效應的方法。Kozhevnikov等[17-22]和Antonov等[23]針對瞬變電磁中的IP效應開展了一系列研究，利用單純形法對頻散均勻半空間等簡單模型的瞬變電磁法響應進行了反演，指出了頻散地層中瞬變電磁響應的反演具有強烈的初始模型依賴，并討論了通過聯(lián)合反演和先驗信息改進反演結果的方法；Yu等[24]利用SVD方法進行了頻散地層中TEM響應的反演，提高了含IP效應的TEM數(shù)據(jù)的解釋精度；顧建寧等[25]利用均勻半空間模型分析了TEM勘探中IP效應的影響規(guī)律，并根據(jù)反號現(xiàn)象直接確定了地下礦體的位置；Chen等[26]利用基函數(shù)擬合和符號約束進行了TEM響應和IP效應的分離，在弱頻散地層上取得了良好的應用效果；陳帥等[27]通過Occam方法緩解了頻散介質(zhì)多參數(shù)引起的欠定性，實現(xiàn)了一維瞬變電磁Occam反演；Zhi等[28]為了解決頻散介質(zhì)中TEM數(shù)據(jù)反演的非單調(diào)問題，引入了粒子群算法進行了TEM數(shù)據(jù)反演目標函數(shù)的全局優(yōu)化，進行了實測數(shù)據(jù)試算，較準確地恢復了頻散地層的電阻率和極化率參數(shù)。

以上研究表明，當前關于頻散效應對瞬變電磁響應的影響機理已經(jīng)較為明確，在數(shù)據(jù)處理方面基本形成了響應曲線分析、頻散響應和感應響應分離、考慮頻散效應的多參數(shù)聯(lián)合反演等三大類方法。其中多參數(shù)聯(lián)合反演方法適用性最廣且解釋精度最高，但由于頻散介質(zhì)中瞬變電磁響應規(guī)律復雜、待求參數(shù)多，多參數(shù)聯(lián)合反演方法具備較強的初始模型依賴。鑒于此，筆者將從頻散介質(zhì)中瞬變電磁響應特征、場隨各參數(shù)變化的單調(diào)性和靈敏度、反演目標函數(shù)特性幾個方面開展分析研究，探究反演方法中強初始模型依賴的原因，為進一步反演策略的合理構建提供理論支持。

1 正演方法

在進行頻散介質(zhì)瞬變電磁正演時，首先進行頻率域電磁場正演，然后通過離散正弦變換得到時域電磁場響應。對于地層頻散特性的模擬，通過Cole-Cole復電阻率模型實現(xiàn)。Cole-Cole模型可同時描述激發(fā)極化和介電極化效應，對于激發(fā)極化效應有：

(1)

如圖1所示建立一維大地模型和笛卡爾坐標系，第i層大地由其電性參數(shù)(σi，mi，ci，τi)和頂面Z坐標Zi唯一確定。采用時諧因子e-iωt，忽略位移電流，則電磁場控制方程可寫為：

圖1 一維大地模型Fig.1 The 1D layered-earth model

(2)

式中：μ為磁導率；ω為角頻率；E和B分別代表電場強度和磁感應強度；J為電流密度矢量。引入庫倫規(guī)范下的磁矢量勢A：

B=▽×A

(3)

(4)

對于電偶極子和圖1的一維模型，磁矢量勢可通過漢克爾變換得到[29]：

(5)

瞬變電磁響應通過傅里葉變換得到，對于常見的TEM階躍發(fā)射波形：

(6)

使用傅里葉變換對：

(7)

其中：F(ω)為頻率域響應；f(t)為時間域響應。由于F(ω)實部和虛部的對稱性，f(t)可以通過實數(shù)域的正弦變換獲取。筆者采用精度較高、計算速度較快的雙精度160點數(shù)字濾波器進行正弦變換，并通過電偶極子疊加技術求取任意形狀發(fā)射回線的瞬變電磁響應[30]。

Lee[10]給出了頻散大地上瞬變電磁響應的漸近表達式，并基于Lornex、Copper cities侵染狀硫化物銅礦和Kidd Creek塊狀硫化物礦床的地電參數(shù)進行了正演計算。為驗證本文算法的正確性，將計算結果與Lee的結果進行了對比。所采用的計算參數(shù)為：重疊回線裝置，發(fā)射線框半徑為25 m，觀測z分量衰減電壓ε，發(fā)射電流為1 A，地電模型參數(shù)見表1。三個地電模型的對比驗證結果如圖2所示，計算結果和Lee的漸近解析解基本吻合，響應曲線的均方相對誤差分別為3.52%、2.76%和5.95%，證明了算法的準確性。衰減曲線在1 ms左右出現(xiàn)的轉(zhuǎn)折代表瞬變電磁響應發(fā)生了符號反轉(zhuǎn)，說明此時頻散效應的放電電流強度超過了感生渦流，且方向與感生渦流相反，符號反轉(zhuǎn)后的觀測電壓主要是頻散效應引起的。

表1 驗證模型地電參數(shù)Tab.1 Geoelectrical parameters of verification models

圖2 正演結果驗證Fig.2 Validation of the modeling results(a)Lornex模型;(b)Copper cities模型;(c)Kidd Creek模型

2 頻散介質(zhì)中瞬變電磁響應特征

基于Lee和Pelton對頻散現(xiàn)象的研究，采用實際工作中常遇到的觀測參數(shù)，設計典型均勻半空間模型，其地電參數(shù)如表2所示。以此為基礎，分別改變電阻率、充電率、時間常數(shù)、頻率相關系數(shù)，研究頻散介質(zhì)中的瞬變電磁響應特征。發(fā)射裝置采用邊長為100 m的中心回線，發(fā)射電流為15 A，觀測衰減電壓z分量。圖3(a)～圖3(d)分別為不同電阻率、充電率、頻率相關系數(shù)、時間常數(shù)均勻半空間的TEM響應曲線。

表2 設計均勻半空間模型的地電參數(shù)Tab.2 Geoelectrical parameters of designed half-space model

從圖3(a)可以看出，地層電阻率越高，TEM曲線符號反轉(zhuǎn)現(xiàn)象出現(xiàn)越早。當電阻率低到一定程度時，觀測時間范圍內(nèi)不出現(xiàn)符號反轉(zhuǎn)現(xiàn)象。這是由于電阻率越高，感應TEM場衰減越快，頻散效應能夠在較早的時間上得以顯現(xiàn)。從圖3(b)可以看出，充電率越高，符號反轉(zhuǎn)現(xiàn)象出現(xiàn)越早。這是因為充電率越高，頻散介質(zhì)儲存能量越大，充放電過程的頻散效應越強。從圖3(c)可以看出，場關于頻率相關系數(shù)的變化特征較為復雜。在頻率相關系數(shù)較小時，隨頻率相關系數(shù)增大，符號反轉(zhuǎn)現(xiàn)象的出現(xiàn)時間逐漸提前；而頻率相關系數(shù)大于一定值之后，符號反轉(zhuǎn)現(xiàn)象出現(xiàn)時間則又逐漸變晚。從圖3(d)可以看出，在時間常數(shù)很小時，觀測時段內(nèi)未出現(xiàn)符號反轉(zhuǎn)現(xiàn)象；隨時間常數(shù)增大，反號現(xiàn)象再次出現(xiàn)且時間逐漸提前，頻散效應增強；當時間常數(shù)大于一定值之后，反號現(xiàn)象出現(xiàn)時刻逐漸變晚，頻散響應減小。當時間常數(shù)很大時，在觀測時間范圍內(nèi)不出現(xiàn)反號現(xiàn)象。不同地電參數(shù)的TEM響應曲線發(fā)生了多次交叉，表明頻散介質(zhì)中的TEM響應隨地電參數(shù)的變化具有較強的非單調(diào)性。

圖3 不同參數(shù)均勻半空間的TEM響應曲線圖Fig.3 TEM response curves of uniform half space with different parameters(a)不同電阻率；(b)不同充電率；(c)不同頻率相關系數(shù)；(d)不同時間常數(shù)

圖4為不同發(fā)射邊長情況下均勻半空間的TEM響應曲線。由圖4可以看出，發(fā)射邊長越大，符號反轉(zhuǎn)現(xiàn)象出現(xiàn)越晚，頻散效應幅值越小。當發(fā)射邊長增大到一定程度時，觀測時間范圍內(nèi)不出現(xiàn)符號反轉(zhuǎn)現(xiàn)象。這是由于隨發(fā)射邊長增加，有效發(fā)射磁矩以二次方增加，感應瞬變電磁場強度顯著增強，導致頻散效應被較強的感應場所掩蓋，僅當感應場衰減到較晚期、幅度大幅減小時才能有所體現(xiàn)。

圖4 均勻半空間不同發(fā)射邊長時的TEM響應曲線圖Fig.4 TEM response curves of uniform half space with different length of transmitting loop

3 瞬變電磁響應函數(shù)的單調(diào)性特征

為研究頻散介質(zhì)中瞬變電磁響應隨地電參數(shù)變化函數(shù)的單調(diào)性特征，仍使用前面設計的均勻半空間模型和觀測參數(shù)，分別將電阻率、充電率、時間常數(shù)、頻率相關系數(shù)作為變量進行正演模擬，結果如圖5～圖8所示。

圖5 隨電阻率變化的TEM響應函數(shù)圖Fig.5 TEM response function of resistivity

圖6 隨充電率變化的TEM響應函數(shù)圖Fig.6 TEM response function of chargeability(a)t=10-5s;(b)t=10-4s;(c)t=10-3s;(d)t=10-2s

圖7 隨頻率相關系數(shù)變化的TEM響應函數(shù)圖Fig.7 TEM response function of frequency dependence(a)t=10-5s;(b)t=10-4s;(c)t=10-3s;(d)t=10-2s

圖8 隨時間常數(shù)變化的TEM響應函數(shù)Fig.8 TEM response function of time constant(a)t=10-5s;(b)t=10-4s;(c)t=10-3s;(d)t=10-2s

圖5為電阻率在10-1Ω·m ～105Ω·m范圍變化時不同時刻的TEM衰減電壓函數(shù)曲線，可以看出當存在頻散效應時，TEM衰減電壓相對于電阻率的函數(shù)為連續(xù)、可導、非單調(diào)函數(shù)。相比于無頻散大地的情況，其非單調(diào)特征更為復雜，其響應函數(shù)包含負值，且至少包含1個極大值點和1個極小值點。

圖6和圖7分別為充電率m和頻率相關系數(shù)c在其定義域[0, 1]范圍內(nèi)變化時，對應不同觀測時刻的TEM響應。由于不同時刻TEM衰減電壓值具有較大的量級差異，為便于觀察分析，將對應觀測時刻t=10-5s、t=10-4s、t=10-3s、t=10-2s的函數(shù)曲線分別繪制為圖6和圖7。從圖6與圖7中可以看出，對于有頻散效應的均勻半空間，其瞬變電磁響應函數(shù)均為非單調(diào)函數(shù)，至少包含1個極值點。

圖8為時間常數(shù)τ在10-8s～105s范圍變化時，對應不同觀測時刻的TEM衰減電壓函數(shù)曲線，此時TEM響應函數(shù)仍為至少包含1個極值點的非單調(diào)函數(shù)。值得注意的是，當時間常數(shù)τ值增大或減小到一定程度后，TEM響應趨于一個定值，對τ值的變化幾乎沒有反映，說明此時瞬變電磁響應對大地介質(zhì)時間常數(shù)的變化“不敏感”。同時隨著觀測時刻增大，瞬變電磁響應隨時間常數(shù)變化較大的“敏感段”逐漸后移，表明瞬變電磁晚期響應對于具有較大時間常數(shù)的頻散效應敏感，而早期響應對于較小時間常數(shù)的快速頻散效應敏感。

4 瞬變電磁場對地電參數(shù)的靈敏度

靈敏度是反問題求解中的重要參數(shù)，用以表征參數(shù)對觀測響應或數(shù)據(jù)的影響程度。為進一步分析頻散介質(zhì)中瞬變電磁響應對不同地電參數(shù)的敏感性，需計算分析各地電參數(shù)的靈敏度。由于不同地電參數(shù)的量綱不同，其靈敏度矩陣也具有不同的量綱。為便于對比，將靈敏度利用響應值進行歸一處理，以衰減電壓為例，歸一靈敏度表示為式(8)。

(8)

其中：p分別代表電阻率ρ、充電率m、頻率相關系數(shù)c、時間常數(shù)τ四個地電參數(shù)。其意義為當?shù)仉妳?shù)p變化1倍時，TEM響應變化的倍數(shù)。

歸一靈敏度作為場對地電參數(shù)的導數(shù)，其變化特征較為復雜，不適合通過函數(shù)圖像呈現(xiàn)。使用上面設計的均勻半空間模型，將對應不同觀測時刻的各參數(shù)靈敏度數(shù)據(jù)列在表3中。

由表3的靈敏度數(shù)據(jù)可以看出，電阻率參數(shù)的靈敏度幅度在觀測時窗范圍內(nèi)差異不大，總體變化范圍約為1個量級，并在5 ms時刻附近達極大值；充電率參數(shù)的靈敏度特征與電阻率參數(shù)類似，但在5 ms時刻附近達到的幅度極大值遠大于其它時刻；頻率相關系數(shù)和時間常數(shù)的靈敏度幅值在不同時刻的變化較大，觀測視窗內(nèi)變化范圍達3個量級以上，在早期靈敏度幅度較小，隨時間推移迅速增加并在5 ms時刻附近達極大值，隨后緩慢降低。各地電參數(shù)的靈敏度變化規(guī)律表明，瞬變電磁響應在全時段上均受地下電阻率和充電率的控制，具有較高的靈敏度值和良好的幅度變化規(guī)律；瞬變電磁響應對于頻率相關系數(shù)和時間常數(shù)具有相對“窄帶”的靈敏度，即僅在與大地時間常數(shù)相當?shù)挠^測時窗范圍內(nèi)具備相對較高的靈敏度，而在偏離該時窗范圍的較早期和晚期，靈敏度較低。

5 頻散介質(zhì)中TEM響應反演特性

前人關于頻散介質(zhì)中瞬變電磁響應的反演研究表明，考慮頻散效應的聯(lián)合反演技術具有很強的多解性，反演結果嚴重依賴于初始模型[18]。為分析此現(xiàn)象產(chǎn)生的原因，筆者采用目前聯(lián)合反演中常用的目標函數(shù)展開計算模擬，分析反演目標函數(shù)的特性。針對聯(lián)合反演中的多解性問題，探討可能的解決方法和途徑。

數(shù)據(jù)的反演實際上是一個將目標函數(shù)最小化的過程，從最佳地擬合觀測數(shù)據(jù)和壓制干擾的角度出發(fā)，一般選取最小二乘目標函數(shù)[22, 27-28]，其一般形式為式(9)。

(9)

其中：d為TEM響應數(shù)據(jù)；Cm為數(shù)據(jù)方差矩陣。

分別取電阻率、充電率、頻率相關系數(shù)、時間常數(shù)的其中兩個參數(shù)作為自變量，計算目標函數(shù)值并繪制函數(shù)圖像。圖9、圖10和圖11分別展示了目標函數(shù)關于地電參數(shù)(ρ，τ)、(ρ，m)、和(ρ，c)變化的三維圖像，可以看出，即使在均勻半空間條件下，目標函數(shù)關于地電參數(shù)的變化也是非單調(diào)的，且響應規(guī)律較為復雜，其函數(shù)圖像呈梯田狀，包含有大量的局部極小；全局極小值唯一，鄰域內(nèi)目標函數(shù)變化梯度較大，全局極小點附近函數(shù)圖形變化尖銳；遠離全局極小的目標函數(shù)梯度迅速減小，函數(shù)圖形趨于平坦。根據(jù)目標函數(shù)特征容易判斷，正是由于大量局部極小點的存在，造成了傳統(tǒng)反演方法具有強多解性和強初始模型依賴的現(xiàn)象，考慮頻散效應的瞬變電磁響應反演難以通過線性最優(yōu)化方法實現(xiàn)。全局最優(yōu)算法可有效地解決局部極小問題，但過度平坦的目標函數(shù)會使得全局優(yōu)化算法難以找到正確的修正方向而難以收斂。因此，還需考慮對目標函數(shù)加以改造，對偏離全局極小的目標函數(shù)值增加懲罰項，或通過參數(shù)約束限制尋優(yōu)范圍，以保證全局尋優(yōu)算法的收斂性。

圖9 目標函數(shù)隨電阻率和時間常數(shù)的變化Fig.9 Objective function varies with resistivity and time constant

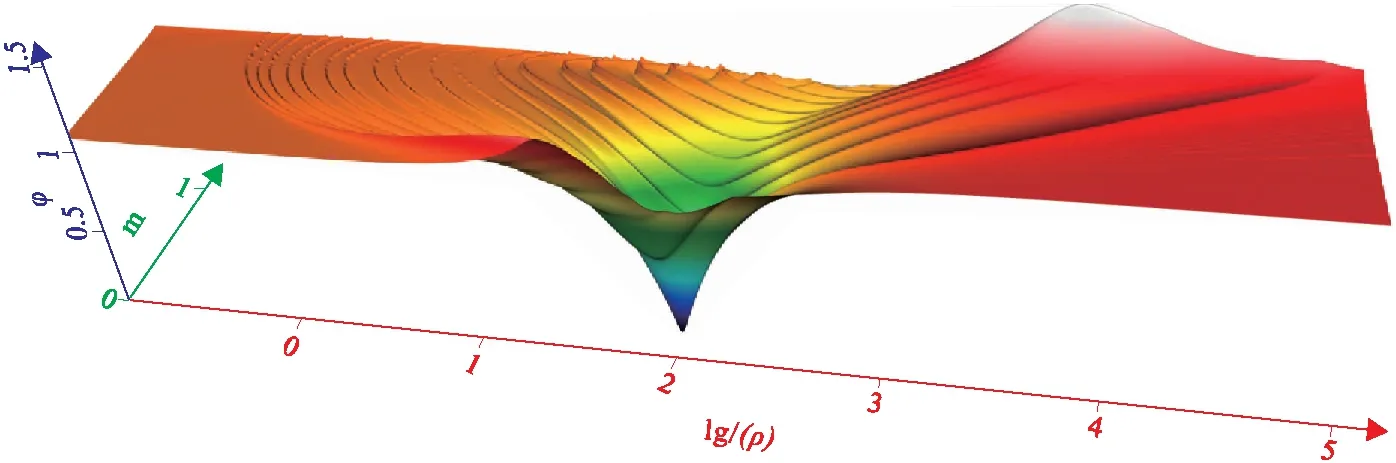
圖10 目標函數(shù)隨電阻率和充電率的變化Fig.10 Objective function varies with resistivity and chargeability

圖11 目標函數(shù)隨電阻率和頻率相關系數(shù)的變化Fig.11 Objective function varies with resistivity and frequency dependence

6 結論

頻散介質(zhì)中的瞬變電磁響應是地層中電磁感應效應和頻散效應相互耦合的綜合效應，響應規(guī)律較為復雜。筆者以一維層狀大地為例，應用Cole-Cole模型和時頻轉(zhuǎn)換技術，實現(xiàn)了頻散介質(zhì)中瞬變電磁響應的正演模擬。結合前人研究和實際工作的常見參數(shù)設計了典型地電模型，研究頻散介質(zhì)中瞬變電磁場的響應規(guī)律及單調(diào)性、靈敏度特征；根據(jù)聯(lián)合反演工作中常用的目標函數(shù)，探討頻散介質(zhì)中瞬變電磁響應的反演特性。主要得出以下認識和結論：

1)基于Cole-Cole模型和數(shù)字濾波技術的頻散介質(zhì)TEM正演方法與Lee所給出的漸近解析解基本吻合，驗證了本文算法的正確性。

2)瞬變電磁響應的符號反轉(zhuǎn)現(xiàn)象代表頻散效應的強度超過了感生渦流場，其產(chǎn)生時刻與大地電阻率、充電率和發(fā)射邊長的關系具有較簡單的相關性，與頻率相關系數(shù)和時間常數(shù)的關系較為復雜。

3)頻散介質(zhì)中瞬變電磁響應隨地電參數(shù)變化的函數(shù)具有連續(xù)、可導、非單調(diào)特征，不存在簡單的線性關系。

4)瞬變電磁場對大地電阻率和充電率的靈敏度較高且幅度特性良好，對于頻率相關系數(shù)和時間常數(shù)具有“窄帶”特征，即僅在與大地時間常數(shù)相當?shù)挠^測時窗范圍內(nèi)，具備相對較高的靈敏度。

5)頻散介質(zhì)中瞬變電磁場反演目標函數(shù)具有大量的局部極小點，是造成傳統(tǒng)聯(lián)合反演存在多解性和強初始模型依賴的主要原因。采用全局最優(yōu)算法可能解決局部極小問題，但需考慮通過引入懲罰項或參數(shù)約束等手段提高全局最優(yōu)算法的收斂性。