大跨“槽型+箱型”連續(xù)混凝土梁受力與設(shè)計研究

顏曉偉

[上海市政工程設(shè)計研究總院（集團）有限公司，上海市200092]

0 引 言

近年來隨著城市交通的發(fā)展，公軌一體化高架得到了廣泛的應(yīng)用和研究[1-2]。目前國內(nèi)公軌一體化高架上層多為城市快速路、下層為軌道交通。簡支槽型梁具有截面空間利用率高、結(jié)構(gòu)整體高度低等特點，在公軌合建下層軌道交通中應(yīng)用廣泛。近年我國在上海、南京、寧波等城市先后進行了大量的工程實踐[3]。

簡支槽型梁跨度小，適用跨徑一般為25～35 m，且結(jié)構(gòu)特殊、受力行為不明確、受力復(fù)雜[4-6]，性能區(qū)別一般混凝土箱梁。為進一步提高槽型梁跨度、明確其受力行為，本文以某地公軌合建工程為背景，采用“槽型+ 箱型”組合截面，設(shè)計35 m+50 m+35 m 大跨“槽型+箱型”組合截面預(yù)應(yīng)力混凝土連續(xù)梁。采用ANSYS 有限元軟件建立三維實體模型，首先研究該組合截面正應(yīng)力分布；其次對組合截面剪力分布、橋面板局部應(yīng)力集中、3 支座支反力分布進行分析；最后對該結(jié)構(gòu)體系橋面板進行配筋設(shè)計。上述研究可為該結(jié)構(gòu)的應(yīng)用和推廣提供一定的參考價值。

1 組合截面設(shè)計及力學(xué)性能

1.1 組合截面設(shè)計簡介

槽型+ 箱型”組合截面包括槽型和箱型兩部分。槽型部分含邊、中腹板，底板（兼做箱型部分頂板）；箱型部分邊、中腹板及底板。邊跨等高段、中跨跨中截面總高度2.775 m（箱型高度1.20 m、槽型高度1.575 m）；中支點處梁總高為4.075 m（箱型高度2.5 m、槽型高度1.575 m），梁高變化段采用二次拋物線；邊跨截面過渡為完全槽型截面（梁高1.975 m），與相鄰標準段簡支槽型梁順接。中腹板厚度統(tǒng)一采用0.8 m；槽型部分邊腹板0.425 m；箱型部分邊腹板跨中為0.4 m，中墩及邊墩支點處厚度為0.5 m；槽型部分底板厚度0.27 m，箱型部分底板厚度由中支點0.6 m 漸變?yōu)榭缰?.27 m，邊支點處增厚為0.49 m。構(gòu)造圖詳見圖1。

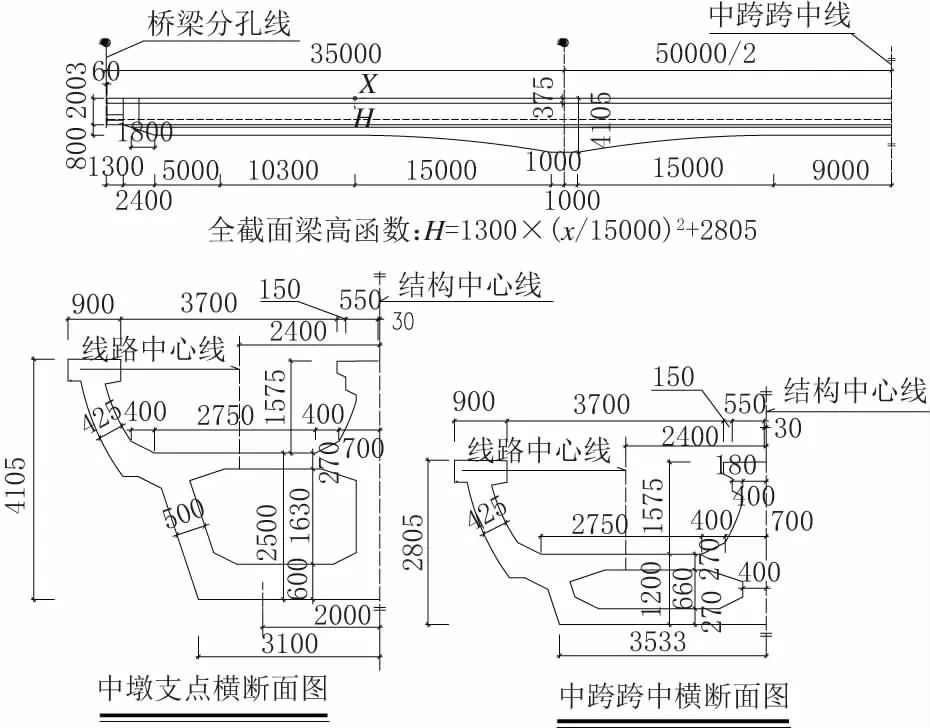
圖1 35 m+50 m+35 m 預(yù)應(yīng)力混凝土連續(xù)梁立面及橫斷面圖（單位：mm）

1.2 有限元模型建立

采用ANSYS 有限元軟件進行建模[7-8]，對全橋結(jié)構(gòu)進行數(shù)值模擬。實體模型共3 115 606 個單元，3 509 844 個節(jié)點；混凝土采用solid45 實體單元模擬，預(yù)應(yīng)力鋼絞線采用link8 單元模擬，ANSYS 模型見圖2、圖3。采用約束方程模擬預(yù)應(yīng)力筋和混凝土間的粘結(jié)；根據(jù)實際支座設(shè)置建立邊界條件；荷載作用位置及大小均按實際情況模擬。

圖2 全橋有限元模型示意圖

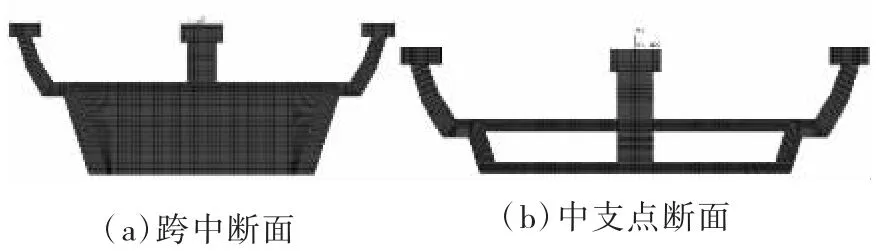
圖3 橫斷面有限元模型示意圖

1.3 縱向正應(yīng)力分布規(guī)律

對于“槽型+ 箱型”組合截面是否滿足平截面假定進行分析。取1/2 中跨分析（長度25 m），考慮在自重作用下（未施加預(yù)應(yīng)力）不同位置處截面縱向正應(yīng)力分布。按照3 m 間距取截面，分析中腹板范圍正應(yīng)力分布，詳見圖4。

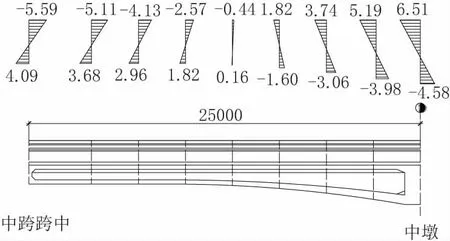
圖4 自重作用下截面正應(yīng)力分布圖（單位：MP a，拉正壓負）

上述分析可知：自重作用下組合截面正應(yīng)力呈線性分布，滿足平截面假定。實際設(shè)計中，如預(yù)應(yīng)力配束等可按照桿系有限元模型進行分析。

2 組合截面受力研究

組合截面結(jié)構(gòu)特殊、受力復(fù)雜，需重點考察截面剪力分布；槽型部分底板與箱型部分橋面板銜接段受力復(fù)雜；該結(jié)構(gòu)橋面板受力不同于箱梁橋面板，應(yīng)予以分析。

2.1 截面剪力分布

組合截面中抗剪主要由槽型、箱型各自邊、中腹板分擔(dān)。基于ANSYS 有限元模型，考慮自重+ 預(yù)應(yīng)力下不同位置、同一位置處截面不同部位剪力值分布，剪應(yīng)力分布如圖5 所示。取1/2 中跨7 個斷面處截面（見圖6），計算結(jié)果見表1。

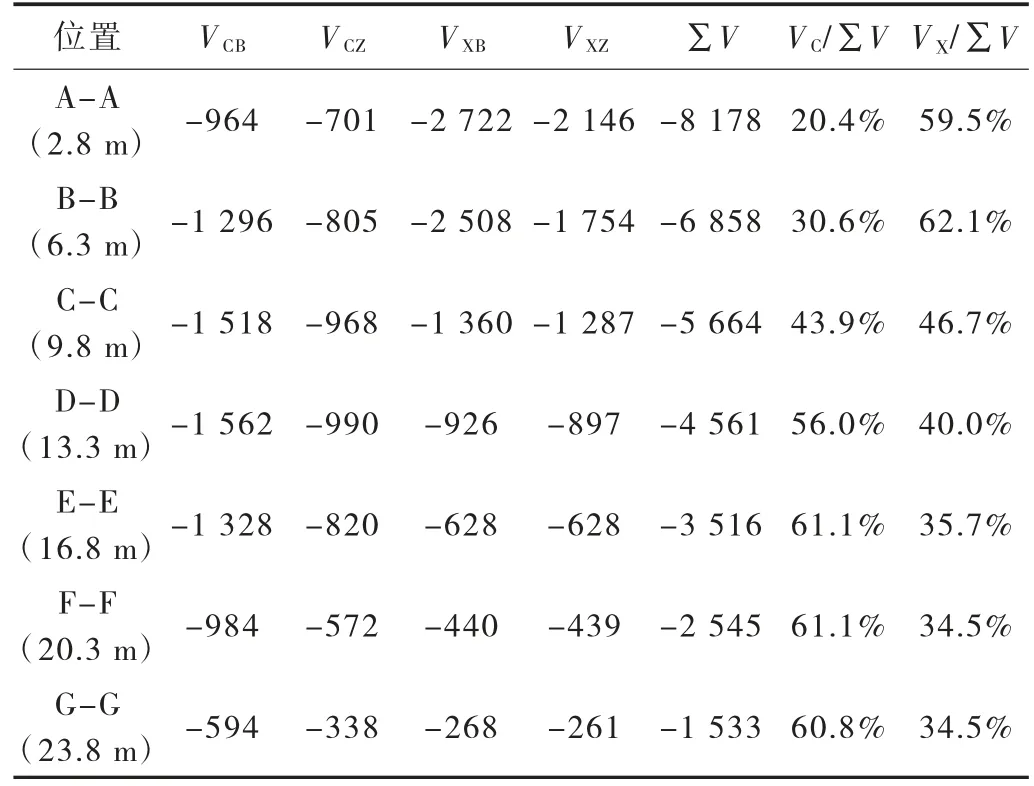
表1 截面剪力值分布表 單位：kN

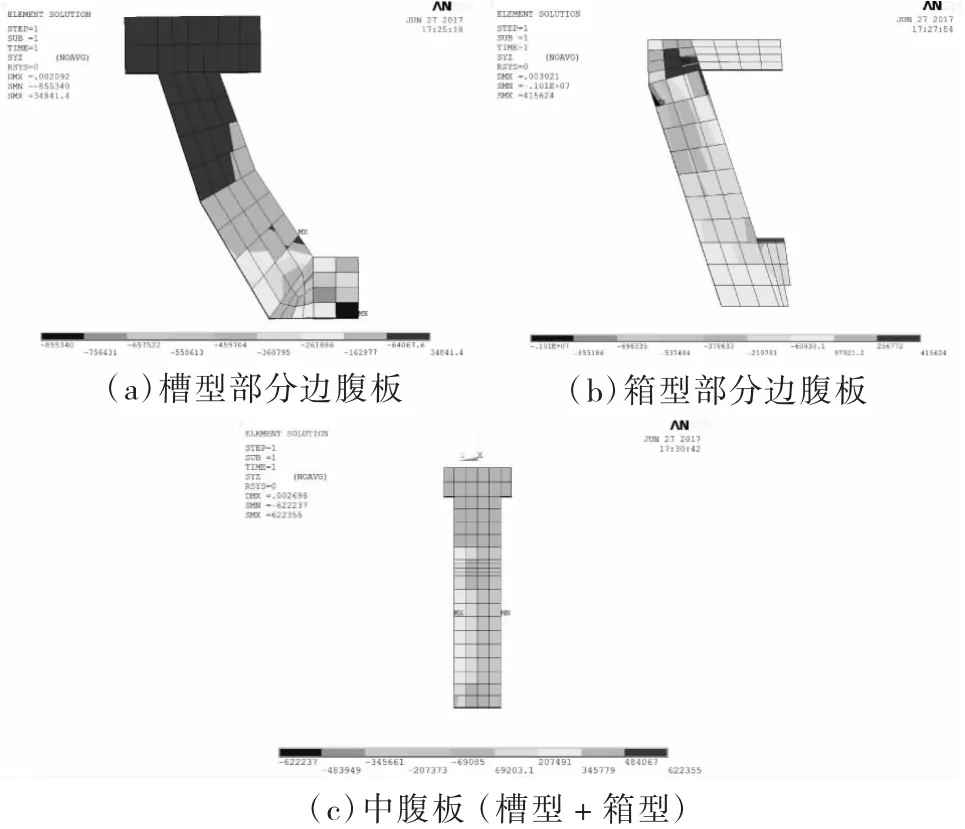
圖5 中支點組合截面不同部位剪應(yīng)力云圖（單位：P a）

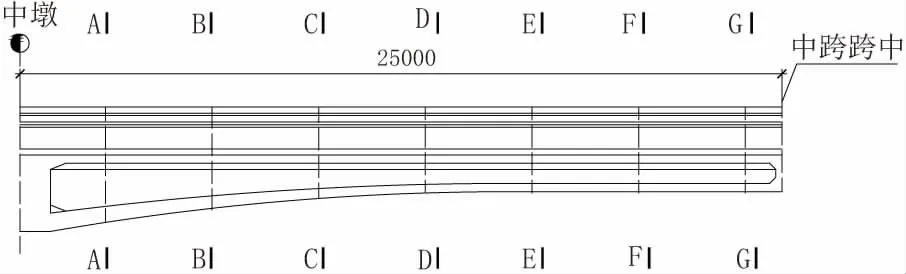
圖6 剪力值計算截取位置

上述計算分析表明：一是中支點附近（A-A、B-B）箱型斷面剪力值為槽型的2～3 倍；D-D 斷面至跨中，槽型部分剪力值大于箱型部分，在跨中附近（F-F～G-G）約為箱型部分的2 倍；二是槽型部分剪力最大值出現(xiàn)在D-D 斷面，約為1/4 跨徑處，箱型部分中支點附近最大；三是槽型、箱型部分邊腹板承擔(dān)的剪力值均大于其中腹板，C-C 斷面向跨中箱型部分邊、中腹板承擔(dān)的剪力值基本相同。根據(jù)上述剪力分布可進一步細化邊、中腹板截面箍筋設(shè)計。

2.2 槽型底板（箱型頂板）受力分析

“槽型+ 箱型”組合截面中槽型底板兼做箱型頂板，槽型部分邊腹板與其底板銜接處受力復(fù)雜，需進行分析。

采用ANSYS 模型分析，計算結(jié)果如圖7 所示。上述計算表明：槽型部分邊腹板與底板銜接處應(yīng)力集中明顯；邊、中墩支點附近處該位置正應(yīng)力達到峰值，計算結(jié)果表明該處承受較大彎矩、剪力值。

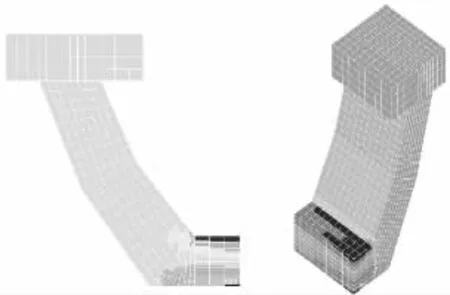
圖7 槽型部分邊腹板與底板銜接處應(yīng)力圖

2.3 邊墩支座反力分布

邊墩為保證與相鄰標準槽型梁順接，過渡為完全槽型截面。為保證支座受力均勻、合理，邊墩支點斷面每道腹板下均設(shè)支座，共設(shè)3 支座，如圖8 所示。根據(jù)有限元模型提取恒載+二期、恒載+二期+列車靜載下支反力，詳見下表2。

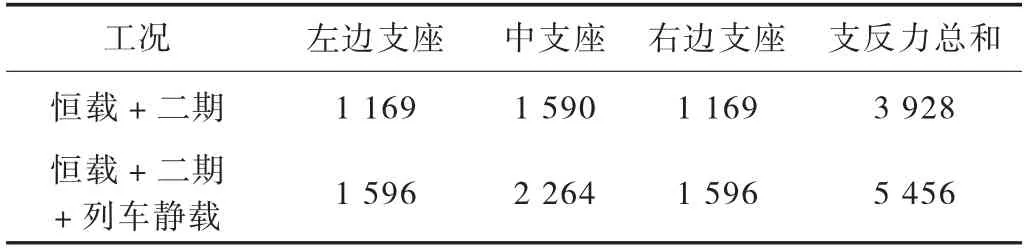
表2 端部支反力分布表 單位：kN

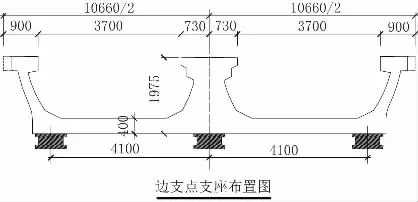
圖8 邊支座布置示意圖（單位：mm）

上述計算結(jié)果表明，左、右支座分擔(dān)支反力約為中支座70%；3 個支座擱置于雙柱柱間橫梁上，該橫梁計算應(yīng)按照上述實際計算支反力值分布加載。

3 橋面板配筋

“槽型+ 箱型”組合截面橋面板同時承受自重、二期、列車活荷載、梯度溫度等。槽型部分邊腹板與底板銜接處應(yīng)力集中明顯，應(yīng)加配筋。橋面板配筋應(yīng)根據(jù)上述銜接處、懸臂端和跨中取包絡(luò)設(shè)計。

根據(jù)ANSYS 模型分別計算三處彎矩值、剪力值，按照鋼筋混凝土構(gòu)件配筋如下，如圖9 所示。

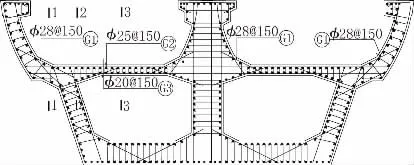
圖9 槽型部分底板（箱型部分）配筋示意圖

（1）槽型邊腹板與底板銜接處1-1 斷面：板厚采用484 mm；該區(qū)域除橋面板鋼筋外，需另設(shè)置#G1鋼筋，直徑28 mm@150 mm 進行加強；同時在中腹板與槽型底板銜接處同樣加強鋼筋。

（2）橋面板懸臂端2-2 及跨中3-3 斷面：板厚分別為470 mm、270 mm；底板頂部#G2 采用直徑25 mm@150 mm，底板底部#G3 直徑20 mm@150 mm。

4 結(jié) 語

以某工程35 m+50 m+35 m 大跨“槽型+ 箱型”組合截面連續(xù)混凝土梁設(shè)計為背景，從組合截面正應(yīng)力分布、截面剪力分布、槽型底板（箱型頂板）不同部位受力、端支點支座反力分布、橋面板配筋進行分析和設(shè)計。主要結(jié)論如下：

（1）“槽型+ 箱型”組合截面在自重作用下截面正應(yīng)力呈線性分布，滿足平截面假定。

（2）組合截面中槽型、箱型腹板剪力分布具有差異性。中支點附近箱型部分梁高較高時，箱型腹板承擔(dān)59.5%～62.2%截面總剪力值，槽型部分腹板承擔(dān)20.4%～30.6%；中跨跨中截面箱型部分梁高較低時，箱型部分腹板承擔(dān)34.5%～35.7%，槽型部分腹板承擔(dān)60.8%～61.1%。

（3）同一斷面處，槽型部分邊腹板分擔(dān)剪力值要大于其中腹板；箱型部分邊腹板與中腹板剪應(yīng)力相差較小。實際工程設(shè)計中需根據(jù)上述剪力分布適當細化邊、中腹板箍筋設(shè)置。

（4）邊墩支點處槽型部分截面設(shè)置3 個支座，左：中：右支座反力比例約為1∶1.42∶1。

（5）通過對槽型底板（箱型頂板）邊腹板與底板銜接處、懸臂根部及跨中彎矩及剪力計算，按鋼筋混凝土構(gòu)件配置橋面板鋼筋。邊腹板與底板銜接段需加強配筋，懸臂根部處及跨中部位配筋可取包絡(luò)設(shè)置。通過合理配筋保證橋面板在運營階段承載力、裂縫均滿足規(guī)范要求。