關于前沿研究融入電動力學課程教學的探索

伏洋洋 董大興 劉友文

（南京航空航天大學理學院 江蘇 南京 211106）

電動力學作為一門經典的理論物理課，很多學生由于基礎沒有打牢，在面對電動力學課程中大量的數學推導，抽象的物理概念時，會覺得難以理解而逐漸失去學習興趣［1］.

另外，教學內容過于陳舊，也很少聯系實際的問題，學生很難有機會運用所學的知識解決一些具體問題，這在一定程度上也降低了學生的學習興趣.如何改進電動力學課程的教學模式，提高學生的學習體驗，促進師生之間的互動交流成為亟需解決的問題［2］.

1 在教學中融入前沿研究的優勢

事實上，每位教師或多或少了解一些與電動力學基礎理論有關的前沿科學研究，完全可以將一些合適的前沿成果融入到電動力學課程教學中.比如，在光學領域蓬勃發展的等離激元光學、光子晶體、變換光學、超構材料、超構表面等前沿研究方向，更是與電動力學的教學內容緊密聯系.在這些前沿研究中，利用計算軟件（比如MATLAB）和數值仿真軟件（如COMSOL MULTIPHYSICS，簡稱：COMSOL）計算電磁場特性、呈現物理圖像也成為主流手段.這些科研工具完全可以引入到電動力學的教學中去.M ATLAB強大的數學處理能力可以實現抽象“物理問題”可視化［3］，能夠讓學生在腦海中呈現清晰的物理圖像，對“不可見的”電磁場形成有效的認知.CO MSOL則充當“虛擬實驗”的角色，可以對具體理論模型的電磁場問題進行仿真模擬［4］，用以檢驗理論的正確性，有效避免了真實實驗中的操作繁瑣、體驗效果差等缺點.

通過在電動力學教學中引入前沿研究成果，并以科研軟件M ATLAB和CO MSOL作為輔助工具，可以有效幫助學生直觀地觀察電磁現象，越過電動力學概念抽象不易理解的門檻，拓展科學視野，并可以進一步培養學生發現問題、思考問題、解決問題的能力.本文將結合一些超構材料研究領域的前沿進展，探討如何在電動力學教學過程中融入相關的前沿科研成果，激發學生們的探索熱情，增強學生對相關基礎知識的深入理解，潛移默化地培養學生的科學素養.下文給出一些具體教學實例，希望能夠給予讀者一些啟發.

2 靜電教學實例

2.1 靜電隱身斗篷

以《電動力學》（第三版 郭碩鴻著）教材第二章靜電場第3節拉普拉斯方程習題2為例：求解介電常數為ε1的介質球置于均勻外電場時的電勢分布，如圖1（a）所示.由拉普拉斯方程得到介質球內外電勢的通解，利用邊界條件，可以求出介質球內外區域的電勢和電場強度.如果學生僅僅滿足數學求解過程而無法清晰理解物理本質，電動力學對于學生來說便只是一門復雜的數學課程.

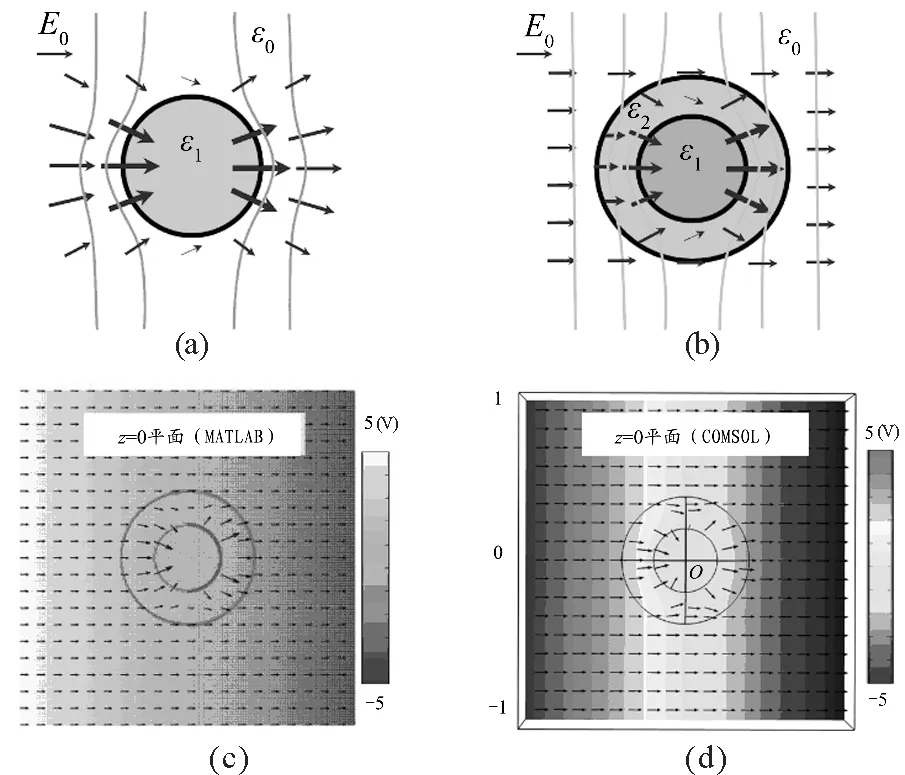
圖1 介質球殼結構實現靜電隱身M ATLAB理論計算和CO MSOL數值仿真

回到例題，我們得到了球內外電勢的解為

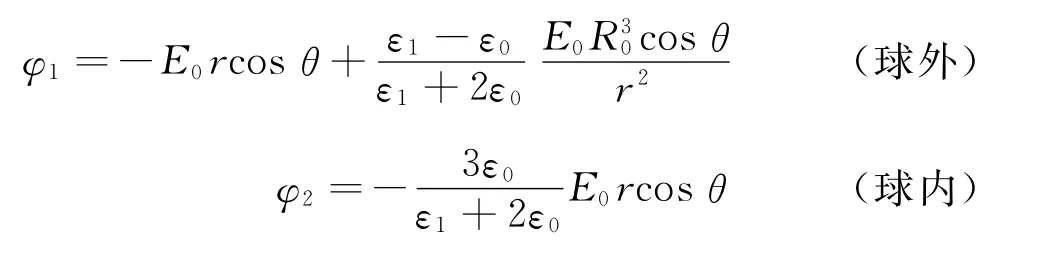
其中，R0為球半徑，r為空間點到球心的距離（球心為坐標原點），ε0為真空介電常數，E0為背景靜電場大小.從該結論出發，我們可以考慮到兩種極端情況：

（1）ε1→-∞，此時介質從數值計算上可近似被看作金屬對待，因而在靜電平衡條件下，球內不再有電場且電勢為零.

（2）ε1=ε0，即介質球被空氣代替時，介質球對源場的影響不復存在，我們對各處電勢的計算回歸到φ=-E0rcosθ.由該點出發，我們可以啟發學生進行思考，是否能夠設計出一種球殼結構，即在介質球外加另一層介質球殼，最終使球外的電場依然為勻強電場，如圖1（b）所示.此時，我們便無法從外部電場的分布判斷介質球是否存在，這也就是所謂的靜電隱身效果［5］.如前文所述，將拉普拉斯方程的通解求解過程拓展到該球殼結構，可解出結構外的電勢分布為

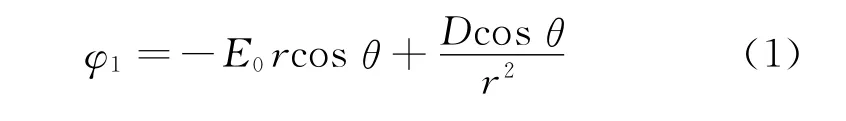
其中

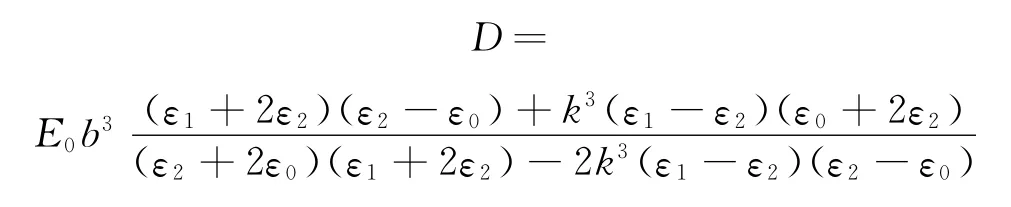
為散射勢場系數，ε2為球殼層的介電常數,為球殼內外半徑比（a和b分別為球殼內半徑和外半徑）.當散射電勢分布為零（D=0），即達成了靜電隱身條件.假定內核球設定為金屬時（ε1→-∞），靜電隱身條件滿足

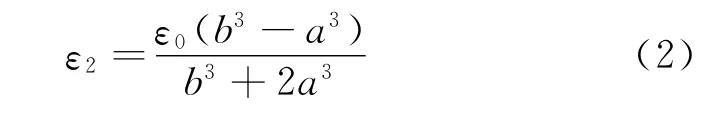
通過該隱身條件，利用M ATLAB可以呈現理論計算的靜電隱身的“物理圖像”.進一步地利用相關參數，結合CO MSOL的模擬實驗可以驗證理論計算的有效性.圖1（c）與圖1（d）是分別使用M ATLAB和CO MSOL展現的球殼在空間中引起的電勢變化及電場強度（顏色分布表示空間電勢變化，黑色箭頭表示電場方向），可以觀察到中心金屬電勢為零，而空間電勢分布以及電場強度分布在球殼結構外是均勻的，所有擾動只存在其內部，因此實現了靜電隱身的效果.基于此，和學生一起探討該靜電隱身的物理本質是分布在兩個內外球面上束縛電荷的等效“偶極子”散射相消的結果.因此，前沿研究在幫助學生深入理解課本例題的同時，也提升其創新意識和能力，對學生今后的學習及科研工作大有裨益.

2.2 靜電場下的有效媒介設計

除靜電隱身問題之外，我們也可選擇性地啟發學生探討靜電場下的有效電介質設計研究.在研究靜電隱身模型時，我們可以引導學生發現：無論單層介質球還是雙層介質球殼外的電勢總是有著相似的表達式cosθ.該表達式由兩部分構成，即背景電勢和介質球引發的散射電勢.若將單層介質球和雙層介質球殼散射勢場系數進行等量匹配，則二者將具有完全相同的電磁響應.物理上來講，雙層介質球殼中的復合電磁參數等價為相同尺寸單層介質球中的均勻有效參數

比如，在設定球殼內外層材料由二氧化硅和銀構成（假定二氧化硅的相對介電常數為2.42，銀為-4.7），只改變球殼內外半徑之比，其等效介電常數可以被有效調節.

圖2（a）和（b）分別是M ATLAB計算的球殼結構（內層為二氧化硅，外層為銀；內層為銀，外層為二氧化硅）的等效介電常數，自變量k為內外半徑比.可以發現，該等效介電常數是可以通過控制半徑比調整的，擴大了可用電磁參數的范圍，也為新型電磁材料的產生提供了渠道.比如，我們以內層為銀，外層為二氧化硅為例［圖2（b）］，當內外半徑比為0.5時，球殼的等效介電常數為-3.1.圖2（c）和（d）是基于CO MSOL數值仿真的有等效介電常數的介質球和復合參數的球殼結構對相同均勻靜電場響應的模擬場圖，二者完全相同（顏色分布表示空間電勢分布，黑色箭頭表示電場方向，坐標原點位于球心），證實了基于M ATLAB中的理論計算.該仿真計算相對簡單，學生們極易上手，能夠幫助學生充分理解等效電磁參數的意義.

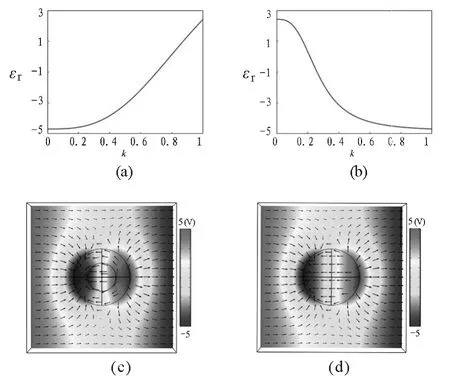
圖2 介質球殼結構的等效介電常數MATLAB計算和COMSOL數值仿真

3 電磁波傳播教學實例

3.1 奇異介質界面的透反射

電磁波傳播作為電動力學教學內容的重要部分，絕大多數教材都會講述電磁波在均勻介質、有耗介質、兩種介質分界面和受限空間（矩形波導）等系統中的傳播性質.以電磁波在介質界面反射、折射一節為例，通過菲涅爾公式，學生學習了不同偏振下的反射系數和透射系數，了解了典型的光學現象，如布儒斯特角、全反射等.如圖3（a）所示，這里可以進一步引導學生掌握有限厚度的電介質平行板的反射系數和透射系數

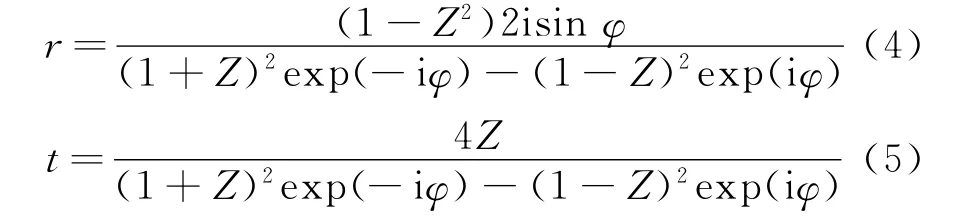
其中Z為阻抗，對于橫電（TE）偏振，Z=對于橫磁（TM）偏振，Z=為介質中垂直平板表面的波數分量，kx為空氣中垂直平板表面的波數分量，ε′和μ′分別為介質板的相對介電常數及相對磁導率.通過對比這兩個體系的反射系數和透射系數的內在聯系，引導學生探討其中的Fab ry-Perot共振機制，如圖3（b）所示.此外，可以進一步引導學生思考在光密到光疏介質環境下，入射波超過其臨界角入射時，一定會出現全反射嗎？是否存在奇異的電磁材料能夠打破常規認識：超過臨界角時，甚至可以無反射波？引導學生分析介質平行板的反射系數，可以發現存在電磁參數復共軛且純虛的超構材料可以實現超過其臨界角時，不會出現全反射現象［6］，并在其滿足一定阻抗條件下實現無反射的電磁場衰減或電磁場放大效應.圖3（c）和（d）是CO MSOL的模擬場圖（顏色分布表示空間電／磁場分布，黑色箭頭表示能流分布，入射波的振幅為1），完美驗證了理論結果：在超構材料電磁參數為ε=0.5i，μ=-0.5i（有效折射率為0.5）且入射角度為39.2°時，TE入射波是實現無反射的電磁場放大效應，而TM 入射波實現了無反射的電磁場衰減效應［6］.此外，該結構體系還具有其他的新奇物理現象值得師生共同探討其中的物理機制.

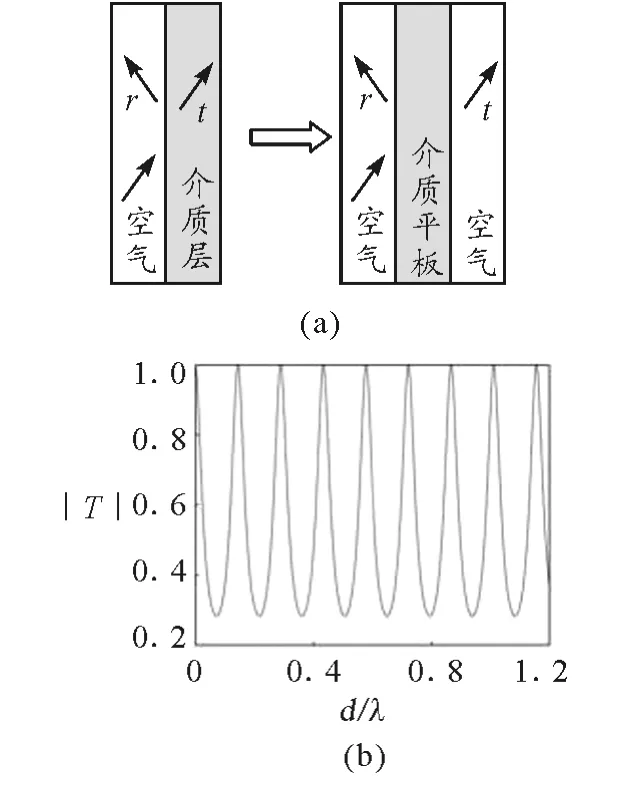
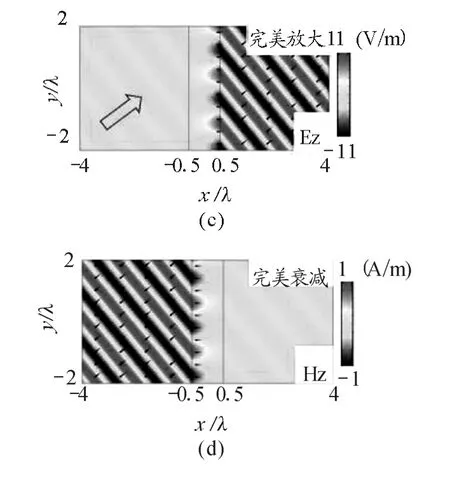
圖3 電介質平行板的Fab ry-Perot共振現象和基于超構材料的無反射電磁場放大／衰減效應

3.2 二維金屬平行板波導

在電磁波傳播的教學內容中，矩形波導中的電磁模式傳播問題相對比較復雜，如圖4（a）所示，通過分離變量等手段求出電磁波導中的特征傳播常數

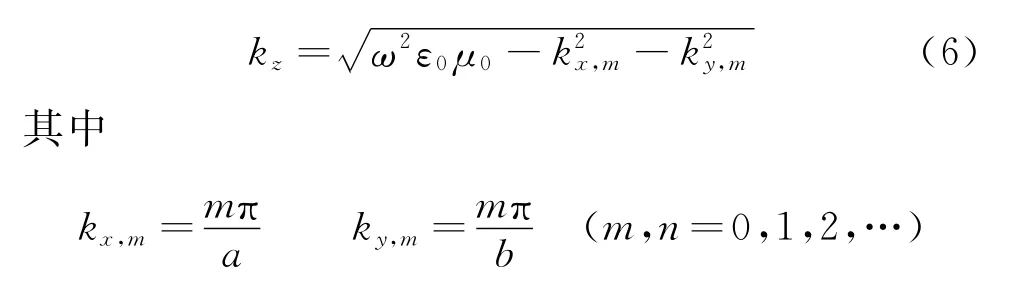
很多教材會在列出截止頻率后，指明三維波導中TE波模式的基模為TE01或TE10模.對于TM波而言，m及n則都不可為零.當x或y方向波導寬度為無限大時，可以啟發學生研究金屬平行板波導［如圖4（b）所示］的電磁模式傳播問題，該情況下的波導傳播常數

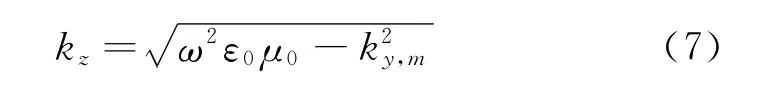
圖4（c）是通過M ATLAB列出的不同波導模式的傳播常數與波數的對應關系，可以發現TE波與TM 波的差異僅在于是否存在零模，也就是說TE波的基模為TE1，而T M 波無截止頻率，其基模為TM0（對應自由空間的TEM模式）.這些結果在CO MSOL的仿真實驗能夠得到證實.從圖4（d）中我們能發現，當我們取圖4（c）中總波數為6.28時，TE0模不存在，TM0模能夠被激發.對于TM1或TE1模式來說，兩種偏振波都能夠被激發.而對于TM2或TE2模式，兩種偏振波是倏逝波，在波導中發生了迅速的衰減而無法傳播.通過CO MSOL數值仿真，學生能夠清晰地觀察到不同波導模式的傳播情況，增加了對課本三維矩形波導傳播規律的深入理解.該二維金屬平行板波導還可以與其他材料結構相結合，引導學生學習不同的物理機制探索一些奇特的波導光學現象.比如，在二維金屬平行板波導中間引入漸變折射率電介質材料，通過波導模式演化機制，實現多樣化的波導功能器件［7］.

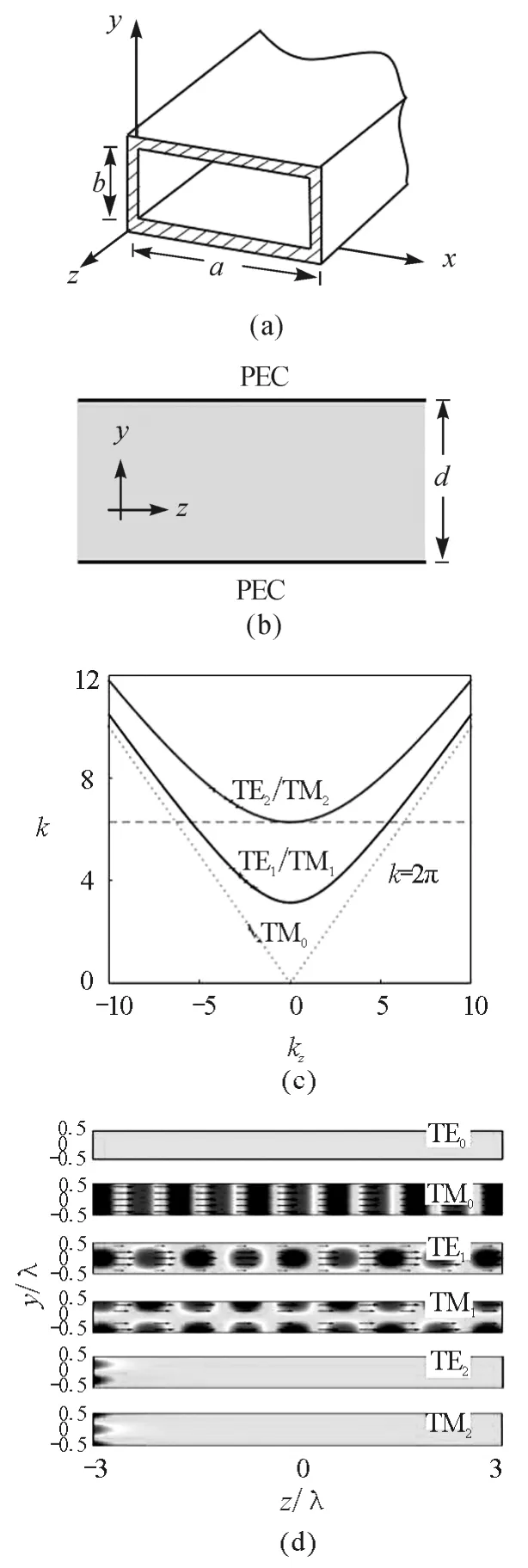
圖4 二維金屬平行板波導傳播模式和模擬場圖

4 結束語

筆者關于前沿研究融入電動力學課程教學的探索和實踐，并通過以上的實例展示，我們可以發現，前沿研究可以讓電動力學的基礎教學內容得到拓展和延伸.科研軟件的使用可以讓教學具有生動性，幫助學生理解抽象的理論知識.依照類似的方法和思路，其他前沿研究成果也可以巧妙地融入到電動力學的基礎教學中去［8］.需要注意的是，針對不同學校的學生能力、水平的差異，相關前沿成果的選擇難度要因地制宜，同時要保證一定的階梯性，能夠讓不同層次的學生都能參與其中，實現不同的發展目標.比如，能力較差的學生可以通過仿真實例的趣味性、操作自由等特點調動他們的學習興趣，鞏固基礎知識；能力較強的學生可以在挑戰學科前沿知識的過程中鍛煉其思維方式、發明創新等能力，能夠形成一定的自主科研能力.前沿研究與電動力學教學結合的案例值得有關高校教師進一步探索，使具有悠久歷史的電動力學課程不斷添加科技發展的新鮮血液，讓電動力學的課程教學能夠實現經典和前沿、基礎和創新、理論和實際的緊密結合，滿足新時代下基礎學科人才培養的需求.