例析等積法的解題技巧

朱紅艷

摘要：初中數(shù)學(xué)中的等積法是一種十分重要的解題思路與方法，其實質(zhì)是一種轉(zhuǎn)換思想，例如運用“兩個三角形等底等高則面積相等”的性質(zhì)，把一些較復(fù)雜的難以直接解決的問題，轉(zhuǎn)化為較簡單的能夠間接解決的問題，從而使問題得到簡捷的解答.本文中結(jié)合四類典型實例，探討和總結(jié)了運用等積法解題的方法與技巧.

關(guān)鍵詞：等積關(guān)系；等積變形；等積互換；等積代換

等積法是等面積法的簡稱，等積法在初中平面幾何類解題中應(yīng)用十分廣泛，例如著名的勾股定理的推導(dǎo)與證明，就是以面積公式及由面積公式推得的相關(guān)性質(zhì)為基礎(chǔ)的.運用等積法解題的關(guān)鍵是，對同一幾何圖形的面積采用不同的分解、計算方法，通過轉(zhuǎn)換與推導(dǎo)得出面積關(guān)系式或者線段與角之間的關(guān)系式.下面通過典型例題來探討并總結(jié)運用等積法解決相關(guān)問題的方法與技巧.

1 運用等積關(guān)系求面積

對于不能直接用公式計算的多邊形面積類問題，通常是在準(zhǔn)確理解題意的基礎(chǔ)上，先畫出示意圖，然后根據(jù)多邊形的性質(zhì)與特點，通過添加輔助線，將多邊形巧妙地分解為若干個三角形，再求出三角形的面積，最后把若干個三角形相加.解題的關(guān)鍵是充分利用由面積公式推導(dǎo)出的相關(guān)性質(zhì)，尋找圖形內(nèi)或圖形之間的關(guān)系[1].

例1已知∠ACB=90°，Rt△ABC的三邊AC，BC，AB的長分別為三個連續(xù)的整數(shù)，以AC為直徑作圓，交AB于點D，過點D作圓的切線交BC于點E，求四邊形ADEC的面積.

解：依題意設(shè)AC=x－1，BC=x，AB=x+1.

因為 ∠ACB=90°，所以 AC2+BC2=AB2.

即（x－1）2+x2=（x+1）2.

解得x1=0（舍），x2=4，即x=4.

所以 AC=3，BC=4，AB=5.

如圖1，連結(jié)CD，因為AC為⊙O的直徑，所以 ∠ADC=90°.所以∠ACB=∠ADC=90°.

又因為∠A=∠A，所以△ACD∽△ABC，從而可得ADAC=ACAB.

所以由AD·AB=AC2，可得AD=325=95，于是BD=AB－AD=5－95=165.

因為 12AB·CD=12AC·BC，所以

CD=AC·BCAB=3×45=125.

因為S△ADC=12AD·CD=12×95×125=5425.

因為AC為直徑，∠ACB=90°，所以BC切⊙O于點C.

又因為DE切⊙O于點D，所以DE=EC，∠CDE=∠ECD.又結(jié)合∠CDE+∠EDB=90°，并且∠ECD+∠B=90°，可得∠EDB=∠B，從而BE=DE.因此EC=12BC.

所以S△DEC=12S△BDC=12×12×165×125=4825.

故S四邊形ADEC=S△ADC+S△DEC=5425+4825=10225.

例2如圖2，已知△BOF，△BOD，△AOF，△COE面積分別為30，35，40，84，求△ABC的面積.

解：設(shè)S△AOE=y，S△COD=x.由面積比關(guān)系，列方程組，得

x+35y+84=3040=34，

x35=y+8470.

解之得x=70，y=56.

所以S△ABC=30+40+35+70+84+56=315.

運用技巧：例1首先利用勾股定理及已知條件“三邊長分別為三個連續(xù)整數(shù)”求得三邊長，然后通過添加輔助線CD，把四邊形ADEC分解為兩個三角形，只要求出兩個三角形的面積即可得到四邊形的面積；例2是運用“數(shù)形結(jié)合”思想，把幾何問題轉(zhuǎn)化為代數(shù)問題，根據(jù)三角形的面積比列出方程組求解，顯得更加簡捷.

2 運用等積變形證面積

在一些平面幾何證明題中，有時需要證明兩個不同圖形的面積相等，這時只需要對待證的圖形進(jìn)行簡單的分割，利用圖形等面積變形或轉(zhuǎn)換的處理，即可使問題得證.

例3如果延長四邊形ABCD的各邊，使A，B，C，D分別成為DE，AF，BG，CH的中點，那么四邊形EFGH的面積是四邊形ABCD面積的幾倍？

解：如圖3，連接AC，BD，BE.因為BA，EB分別是△EBD與△AEF的中線，所以S△BAE=S△BAD，S△EFB=S△BAE.

所以S△AEF=2S△BAD.

同理可得

S△BFG=2S△ABC，S△CGH=2S△BCD，S△DHE=2S△CDA.

所以S△AEF+S△BFG+S△CGH+S△DHE+S四邊形ABCD

=2（S△ABD+S△ABC+S△BCD+S△CDA）+S四邊形ABCD

=2×2S四邊形ABCD+S四邊形ABCD.

即S四邊形EFGH=5S四邊形ABCD.

答：四邊形EFGH的面積是四邊形ABCD面積的5倍.

例4如圖4，已知在四邊形ABCD中，AC，BD交于點E，延長DB到點G，使BG=DE，延長CA到點F，使AF=CE，連接FG.

求證：S△EFG=S四邊形ABCD.

證明：連接AG，CG.

因為BG=DE，又△ABG與△ADE有共同頂點A，所以S△ABG=S△ADE.

同理，S△AFG=S△CGE，S△CBG=S△CDE.

所以S△CDE+S△CEB=S△CBG+S△CEB.

即S△CDB=S△CEG.

所以S△EFG=S△ABG+S△AFG+S△ABE=S△ADE+S△CEG+S△ABE=S△ADE+S△CDB+S△ABE=S四邊形ABCD.

運用技巧：例3和例4都是證明三角形與四邊形的面積之間存在某種關(guān)系，都運用了等積變形的方法.先將四邊形分割成若干個小三角形，而這些小三角形面積又成對相等；最后采用等積代換與組合的方法，證明了三角形與四邊形之間的面積關(guān)系.

3 運用等積互換證線段

對于有些難以直接證明的兩條（或幾條）線段相等的問題，可以采用間接證明的方法，先證明兩個圖形的面積相等，再由這兩個圖形的相關(guān)線段相等，推證出待證的兩條線段也相等.

例5如圖5，已知D是△ABC內(nèi)∠BAC平分線上的一點；CE∥DB，交AB的延長線于點E；BF∥DC，交AC的延長線于點F.求證BE=CF.

證明：如圖6，設(shè)CE與BF的交點為G.連接DG，DE，DF.

因為D是∠BAC平分線上的點，所以∠BAD=∠DAC.過D分別作DM⊥AB，DN⊥AC，M，N為垂足，則DM=DN.

因為CE∥DB，BF∥DC，所以四邊形CDBG為平行四邊形，于是S△BDG=S△CGD.

又因為BD∥CE，所以S△BDE=S△BDG.

同理，可證S△DCF=S△DCG.

因此S△BDE=S△DCF，即

12BE·DM=12CF·DN.

所以BE=CF.

例6如圖7，在△ABC中，點A′，B′，C′分別在邊BC，CA，AB上，AA′，BB′，CC′交于點O，且AOOA′+BOOB′+COOC′=92.

求AOOA′·BOOB′·COOC′的值.

解：令x=S△BOC，y=S△COA，z=S△AOB，則

AOOA′=z+yx，BOOB′=x+zy，COOC′=y+xz.

所以

AOOA′·BOOB′·COOC′

=（z+y）（x+z）（y+x）xyz

=z+yx+x+zy+y+zz+2

=AOOA′+BOOB′+COOC′+2.

=92+2=94.

運用技巧：例5、例6運用了等積變換法.例5首先證明了兩個三角形面積相等，而這兩個三角形的高又是已知且相等的，然后推證出它們的底相等，最后推證出兩條線段相等；例6利用了“等底”或“等高”的三角形的面積比，將線段比轉(zhuǎn)化為面積比，最后又將面積比轉(zhuǎn)換為線段比的新的關(guān)系，證法更加巧妙靈活.

4 運用等積代換作圖

運用等積代換的方法，可以按照題目的要求，作一個m邊形，使它和已知n邊形的面積相等.

例7作一個四邊形，使它和已知的五邊形面積相等.

已知：五邊形ABCDE（如圖8），求作一個四邊形，使它和五邊形ABCDE面積相等.

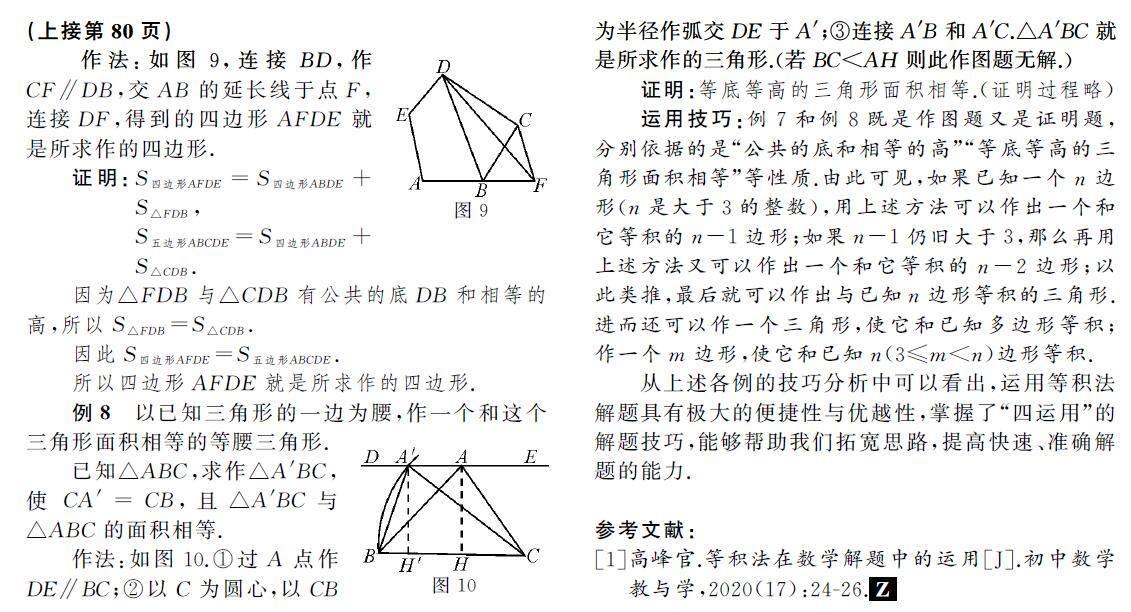
作法：如圖9，連接BD，作CF∥DB，交AB的延長線于點F，連接DF，得到的四邊形AFDE就是所求作的四邊形.

證明：S四邊形AFDE=S四邊形ABDE+S△FDB，

S五邊形ABCDE=S四邊形ABDE+S△CDB .

因為△FDB與△CDB有公共的底DB和相等的高，所以S△FDB=S△CDB.

因此S四邊形AFDE=S五邊形ABCDE.

所以四邊形AFDE就是所求作的四邊形.

例8以已知三角形的一邊為腰，作一個和這個三角形面積相等的等腰三角形.

已知△ABC，求作△A′BC，使CA′=CB，且△A′BC與△ABC的面積相等.

作法：如圖10.①過A點作DE∥BC；②以C為圓心，以CB為半徑作弧交DE于A′；③連接A′B和A′C.△A′BC就是所求作的三角形.（若BC

證明：等底等高的三角形面積相等.（證明過程略）

運用技巧：例7和例8既是作圖題又是證明題，分別依據(jù)的是“公共的底和相等的高”“等底等高的三角形面積相等”等性質(zhì).由此可見，如果已知一個n邊形（n是大于3的整數(shù)），用上述方法可以作出一個和它等積的n-1邊形；如果n-1仍舊大于3，那么再用上述方法又可以作出一個和它等積的n-2邊形；以此類推，最后就可以作出與已知n邊形等積的三角形.進(jìn)而還可以作一個三角形，使它和已知多邊形等積；作一個m邊形，使它和已知n（3≤m

從上述各例的技巧分析中可以看出，運用等積法解題具有極大的便捷性與優(yōu)越性，掌握了“四運用”的解題技巧，能夠幫助我們拓寬思路，提高快速、準(zhǔn)確解題的能力.

參考文獻(xiàn)：

[1]高峰官.等積法在數(shù)學(xué)解題中的運用[J].初中數(shù)學(xué)教與學(xué)，2020（17）：24-26.