培養問題意識，提升活動課的有效性

陳飛

綜合實踐活動課是激發學生主動參與學習，培養學生觀察和發現問題，提出問題，應用所學知識解決問題的重要途徑.因此綜合實踐活動課已經得到了越來越多教師的重視，那么如何才能提高活動課的有效性呢？在日常教學中我們不難發現，綜合實踐活動課的教學或是流于形式，表面熱鬧，或是應付任務，按部就班，大大削弱了活動課的有效性，也浪費了教學時間.筆者在教學中進行了一些實踐和思考，下面以折紙類綜合實踐活動課為例，談一談如何進行有效地教學，與各位同仁討論交流.

1 折紙實踐活動課設計

1.1 用矩形紙片折等腰三角形——認識軸對稱的性質（1）嘗試將一張矩形A4大小的紙片按照圖1-1的方法進行折疊，請問折疊之后形成重疊的△BED是等腰三角形嗎？

解析：由折疊可知，∠1和∠2相等，因為AB和CD平行，所以∠1和∠3相等.通過等量轉換可以得到∠2和∠3相等，由此DE和BE相等，所以△BED是等腰三角形.

（2）再將一張矩形A4大小的紙片ABCD按照圖1-2中的方法進行折疊，請問折疊之后形成重疊的△ECF是等腰三角形嗎？

解析1：通過第（1）題的證明方法可以得到△ECF是等腰三角形.

解析2：根據折疊可以得到AD與CD′相等，又AD與BC相等，可以得到CD′與CB相等.由折疊可以得到∠D和∠D′都是直角，且∠B也等于90°，∠ECD′與∠A，∠BCD都等于90°，因此∠D′CF與∠BCE相等.由此可以得到△D′CF與△BCE全等（ASA），所以CF與CE相等，因此△CEF是等腰三角形.

同樣第（1）題也可以由全等三角形得到結論.

（3）圖1-1中的△BED和圖1-2中△ECF的面積相等嗎？請說明你的理由.

解析：猜想△BED和△ECF的面積相等.假設BC和DC的長度分別是a和b.圖1-1中，DE和BE相等，設為x，則A′E等于b－x，在Rt△A′DE中，根據勾股定理，可得x=a2+b22b，即DE的長度為a2+b22b.圖1-2中，設CF的長度為y，則DF與D′F相等為b－y，在Rt△FCD′中，根據勾股定理可得y=a2+b22b，即CF的長度為a2+b22b.因此由面積公式可以得到△BED和△ECF的面積相等.

設計意圖：通過折疊矩形紙片的活動來進行等腰三角形的研究，可以讓學生在動手操作中體會軸對稱的性質.在折疊操作之后繼續進行追問，使學生意識到實踐活動并不只是簡單的動手操作，還需要進行觀察思考和理論證明，由此加深之前動手操作形成的不夠清晰的認識或者糾正在頭腦中形成的片面的認識，讓學生對數學結論有更加深入的理解，提升邏輯推理能力，培養科學嚴謹的精神.

1.2 巧用數學習題，用正方形折出分數13

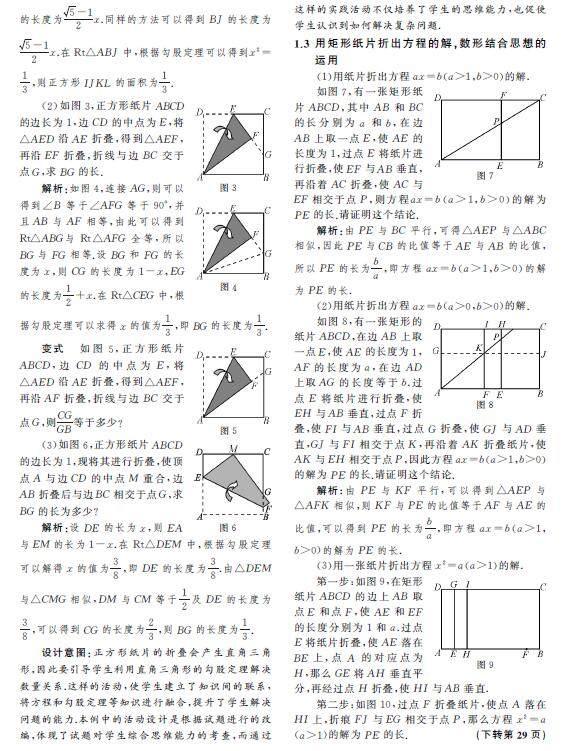
（1）如圖2，正方形紙片ABCD，邊長為1，各邊的黃金分割點分別為E，F，G，H，已知AE小于EB，BF小于FC，CG小于GD，DH小于HA，沿AF，BG，CH和DE進行折疊，得到正方形IJKL，請問正方形IJKL的面積是多少？

解析：因為EI平行于BJ，點E是AB的黃金分割點，所以AEEB=AIIJ=5－12.設IJ的長度為x，則AI的長度為5－12x.同樣的方法可以得到BJ的長度為5－12x.在Rt△ABJ中，根據勾股定理可以得到x2=13，則正方形IJKL的面積為13.

（2）如圖3，正方形紙片ABCD的邊長為1，邊CD的中點為E，將△AED沿AE折疊，得到△AEF，再沿EF折疊，折線與邊BC交于點G，求BG的長.

解析：如圖4，連接AG，則可以得到∠B等于∠AFG等于90°，并且AB與AF相等，由此可以得到Rt△ABG與Rt△AFG全等，所以BG與FG相等.設BG和FG的長度為x，則CG的長度為1－x，EG的長度為12+x.在Rt△CEG中，根據勾股定理可以求得x的值為13，即BG的長度為13.

變式如圖5，正方形紙片ABCD，邊CD的中點為E，將△AED沿AE折疊，得到△AEF，再沿AF折疊，折線與邊BC交于點G，則CGGB等于多少？

（3）如圖6，正方形紙片ABCD的邊長為1，現將其進行折疊，使頂點A與邊CD的中點M重合，邊AB折疊后與邊BC相交于點G，求BG的長為多少？

解析：設DE的長為x，則EA與EM的長為1－x.在Rt△DEM中，根據勾股定理可以解得x的值為38，即DE的長度為38.由△DEM與△CMG相似，DM與CM等于12及DE的長度為38，可以得到CG的長度為23，則BG的長度為13.

設計意圖：正方形紙片的折疊會產生直角三角形，因此要引導學生利用直角三角形的勾股定理解決數量關系.這樣的活動，使學生建立了知識間的聯系，將方程和勾股定理等知識進行融合，提升了學生解決問題的能力.本例中的活動設計是根據試題進行的改編，體現了試題對學生綜合思維能力的考查，而通過這樣的實踐活動不僅培養了學生的思維能力，也促使學生認識到如何解決復雜問題.

1.3 用矩形紙片折出方程的解，數形結合思想的運用（1）用紙片折出方程ax=b（a>1，b>0）的解.

如圖7，有一張矩形紙片ABCD，其中AB和BC的長分別為a和b，在邊AB上取一點E，使AE的長度為1，過點E將紙片進行折疊，使EF與AB垂直，再沿著AC折疊，使AC與EF相交于點P，則方程ax=b（a>1，b>0）的解為PE的長.請證明這個結論.

解析：由PE與BC平行，可得△AEP與△ABC相似，因此PE與CB的比值等于AE與AB的比值，所以PE的長為ba，即方程ax=b（a＞1，b＞0）的解為PE的長.

（2）用紙片折出方程ax=b（a＞0，b＞0）的解.

如圖8，有一張矩形的紙片ABCD，在邊AB上取一點E，使AE的長度為1，AF的長度為a，在邊AD上取AG的長度等于b.過點E將紙片進行折疊，使EH與AB垂直，過點F折疊，使FI與AB垂直，過點G折疊，使GJ與AD垂直，GJ與FI相交于點K，再沿著AK折疊紙片，使AK與EH相交于點P，因此方程ax=b（a＞1，b＞0）的解為PE的長.請證明這個結論.

解析：由PE與KF平行，可以得到△AEP與△AFK相似，則KF與PE的比值等于AF與AE的比值，可以得到PE的長為ba，即方程ax=b（a＞1，b＞0）的解為PE的長.

（3）用一張紙片折出方程x2=a（a>1）的解.

第一步：如圖9，在矩形紙片ABCD的邊上AB取點E和點F，使AE和EF的長度分別為1和a.過點E將紙片折疊，使AE落在BE上，點A的對應點為H，那么GE將AH垂直平分，再經過點H折疊，使HI與AB垂直.

第二步：如圖10，過點F折疊紙片，使點A落在HI上，折痕FJ與EG相交于點P，那么方程x2=a（a＞1）的解為PE的長.

解析：如圖11，連接AK，設AK與FJ相交于點P′，過點P′作P′E垂直于AB.因為AP′與P′K相等，所以P′E與KH平行.因為AH的中點為E′，所以E與E′重合.因此P′與P重合，所以AK經過點P，AK被FJ平分.在Rt△AFP中，根據射影定理可得，PE2=AE×EF=a.由此方程x2=a（a＞1）的一個解為PE的長，另一個解是它的相反數.

設計意圖：解方程是初中數學的重要內容，也是學生熟悉的題型，通過將折紙與方程相結合，提升了問題的難度，增加了挑戰性，也是對學生思維的一次訓練.教師可以在操作前進行示范，引導學生觀察折疊之后的邊角關系，幫助學生將所學知識應用到折紙的操作中去，從而巧妙地將折紙和解方程相結合.這樣的活動可以激發學生的好奇心，也是對學生進行數形結合思想方法的滲透，提升學生解決問題的能力.

2 折紙類綜合實踐活動的教學反思

綜合實踐活動課需要學生的積極參與.因此，首先需要激發學生的學習興趣和探究的好奇心.在教學中教師可以通過問題串的設計，激發學生的求知欲，讓學生在解決問題中再次提出問題，觸發思維的生長點.其次，綜合實踐活動課需要有明確的教學目標，活動環節的設計需要由淺入深、層層遞進，這樣才能一步步實現活動的目標.筆者認為在開展這類活動時有以下幾點需要引起注意.

（1）聯系教材，提升思維

綜合實踐活動課的目的是為了鞏固所學知識，提升思維能力.本課中通過折紙活動，結合教材中的等腰三角形的判定、解方程、幾何圖形的性質等知識解決問題，既能提升學生運用知識的能力，又將操作實踐與思維發展相結合，實現了活動目標和活動內容的統一，提升了活動的有效性.

（2）活動形式豐富多樣，增強教學的實效性

通過實踐活動進行探索并在教師的引導下進行理論證明，是獲得數學結論的重要途徑，二者相輔相成，互相促進.通過折紙實踐活動，學生進一步深入認識幾何圖形，理解幾何圖形中邊、角之間的關系;在分析和證明的過程中，進一步掌握分析問題和解決問題的方法，理解數學折疊問題的實質.

（3）設計活動科學合理，關注分層教學

提高數學實踐活動課的有效性需要關注到全體學生，針對不同層次的學生設計有效的活動，激發學生的學習興趣，讓不同的學生都能感受到收獲的喜悅.在教學中可以通過有效的問題推進教學活動，注意變式訓練，通過一題多解培養學生的發散性思維，讓每一位學生都能真正得到發展.

總之，綜合實踐活動課的開展要圍繞以下幾個問題進行思考：開展什么內容的綜合實踐活動？如何設計綜合實踐活動？怎樣才能更好地開展活動？怎樣才能真正提升活動的有效性，達成教學目標？