鋼桁腹-混凝土組合箱梁的約束扭轉剪應力分析

石國慶，丁南宏，陳 磊

（蘭州交通大學 土木工程學院，甘肅 蘭州 730070）

鋼桁腹-混凝土組合箱梁作為一種新型的鋼混組合結構，是由混凝土頂底板、鋼腹桿和內外預應力筋構成并共同工作的組合結構體系。與傳統混凝土箱梁相比，具有降低自重、有效避免腹板開裂、抗風性能好、降低造價和結構美觀等諸多優點。2013年，國內第一座鋼桁腹-混凝土組合箱梁橋——南京江山橋建成通車。目前已有國內學者對鋼桁腹-混凝土組合箱梁結構進行了相關的力學性能研究和節點構造研究[1-5]，但對于鋼桁腹-混凝土組合箱梁剛性扭轉產生的約束扭轉剪應力鮮有研究。在組合箱梁中考慮鋼腹桿主要承受抗剪作用，王彤等[6]基于鋼桁腹桿在豎向剪切剛度一致的原則，提出一種將鋼腹桿等效為連續鋼板的方法，結合薄壁箱梁理論建立了該橋型在彎曲、扭轉和畸變等方向的理論計算方法。文獻[7-8]中考慮了鋼腹桿在縱向上的變形條件，提出了換算鋼腹板縱向表觀彈性模量的計算方法，推導了鋼桁腹式混凝土組合箱梁的約束扭轉翹曲正應力表達式并結合有限元進行了驗證。國內外對閉口薄壁桿件約束扭轉剪應力的研究較為成熟[9]。本文通過結合薄壁桿件的扭轉性能研究方法，對鋼桁腹-混凝土組合箱梁的約束扭轉剪應力分布情況進行初步探究。

對鋼桁腹-混凝土組合箱梁的約束扭轉分析作如下的基本假定。

（1）鋼腹桿為二力桿，僅承受剪力且受力均勻；

（2）荷載產生的彎矩僅由頂底板承擔；

（3）忽略鋼腹桿自身的扭轉，不考慮失穩；

（4）組合箱梁橫截面符合周邊不變形假定，且各構件受力均在彈性范圍內；

（5）橫截面上的法向應力和剪應力沿壁厚呈均勻分布。

1 鋼桁腹桿的力學特性

1.1 鋼桁腹桿的等效換算

鋼桁腹-混凝土組合箱梁的腹桿布置形式多樣，本文研究的腹桿布置形式為斜腹桿，基于截面剪切剛度一致的原則[6]，將鋼腹桿等效為連續鋼腹板，則換算鋼腹板厚ts為：式中，Es為鋼腹桿彈性模量；Gs為鋼腹桿剪切模量；As為鋼腹桿截面面積，d為鋼腹桿長度，b和h分別為鋼腹桿水平和豎直投影長度。

由于換算鋼腹板與混凝土頂底板材料不一致，為簡化計算，將鋼腹板換算為混凝土腹板，根據截面總剪力與剪應變不變的原則，得到換算混凝土腹板厚度tc為：

式中，Gc為等效混凝土腹板剪切模量；ns為換算鋼腹板與換算混凝土腹板剪切模量的比值。

1.2 鋼桁腹桿縱向表觀彈性模量

基于鋼腹桿縱向變形與等效鋼腹板縱向位移相等的原則[7]，鋼桁腹桿縱向表觀彈性模量Ex表達式為：式中，Is為鋼腹桿截面慣性矩，α為鋼桁腹桿之間的夾角。

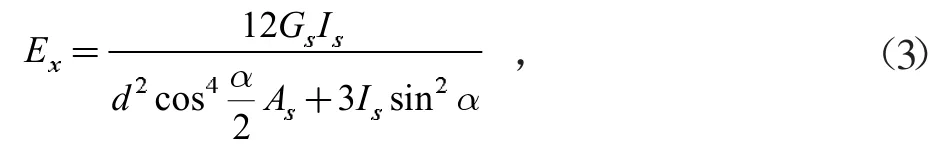
2 約束扭轉剪應力分析

取換算為混凝土腹板之后的組合箱梁薄壁微元體，如圖1所示。

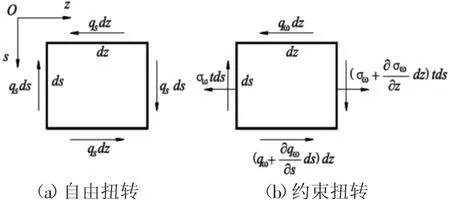
圖1 等效箱壁微元體

圖3（a）中qs為自由扭轉產生的剪力流，

式中，MS為自由扭矩，θ′（z）為扭率；Ω為閉口截面面積的2倍。

圖1（b）中qω為約束扭轉剪力流，根據微元體在z方向上合力為0，可得：

式中，nc為混凝土彈性模量與鋼腹板縱向表觀彈性模量的比值。

對約束扭轉雙力矩B?微分可得彎扭力矩M?：

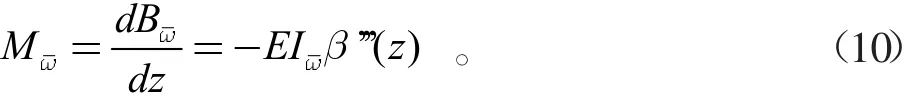
將式（10）代入式（7）中，翹曲剪力流可表示為：

將式（12）代入式（11）中，可求解出二次剪力流：

在計算組合箱梁的扭轉剪應力時，頂板懸臂板屬于開口截面，故計算這部分的廣義主扇性靜矩時，不計帶

薄壁箱梁受約束扭轉時，截面總剪流由自由扭轉剪力流qs和約束扭轉翹曲剪力流qw兩部分組成，則約束扭轉總剪力流為：

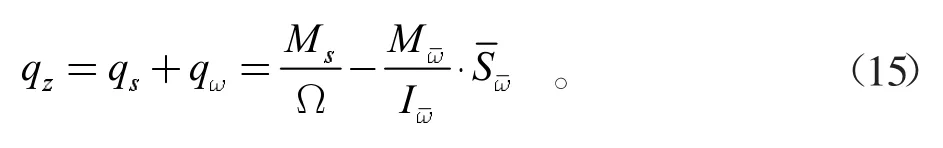
對于鋼桁腹-混凝土組合箱梁而言，因材料不同，使混凝土頂底板和換算鋼腹板的計算分析有所不同。對于換算鋼腹板，由于縱向表觀彈性模量Ex相對鋼板材料的彈性模量Es較小，故縱向應力較小，可視為只有自由扭轉產生的剪應力，故根據式（15），可進一步求得混凝土頂底板的約束扭轉剪應力τc和換算鋼腹板的約束扭轉剪應力τ0分別為：

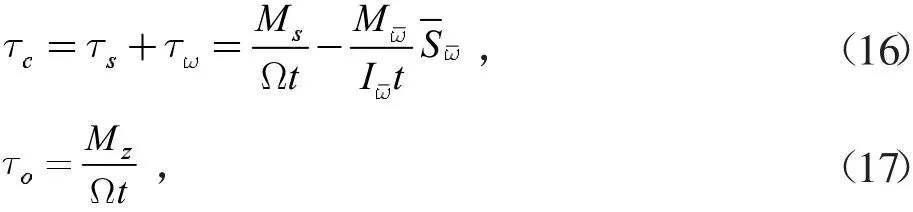
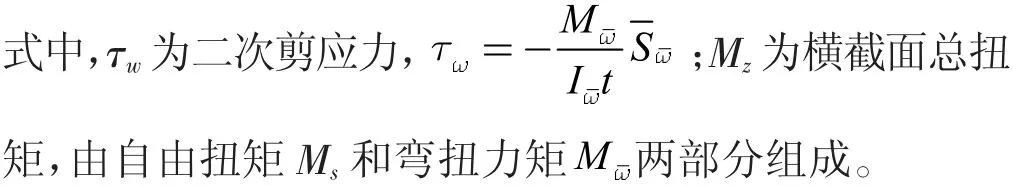
3 約束扭轉微分方程

利用內外扭矩平衡條件及變形協調條件可得到θ（z）與β′（z）之間的關系式，再根據截面總扭矩Mz為自由扭矩Ms和彎扭力矩之和，可建立約束扭轉微分方程[10]：

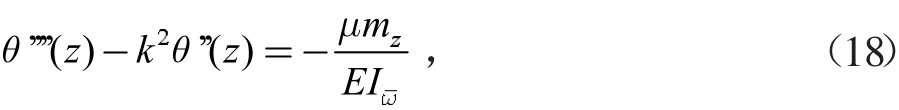
式中，μ為截面約束系數，μ=1-Id/Iρ，Id為抗扭慣性矩，Iρ為極慣性矩；k表示約束扭轉的彎扭特征系數，為分布外扭矩集度。

采用初參數法結合邊界條件對約束扭轉微分方程進行求解[11-12]，可求得等參數，進一步可求得，進而解出約束扭轉剪應力。

4 數值算例分析

4.1 算例簡介

選取某簡支單箱單室鋼桁腹-混凝土組合箱梁為算例，荷載及跨徑如圖2所示，計算跨徑l=35 m，標準橫截面如圖3所示。鋼桁腹桿選用Q345C級鋼管，規格均為Φ351×16，腹桿縱斷面內水平傾角大約為67°，腹桿節間距為195 cm；混凝土頂底板采用C50混凝土。在跨中頂板與鋼桁腹桿交界處施加豎向偏心荷載p=250 kN，偏心距e=207.5 cm，集中扭矩Mk=pe。材料性質：混凝土彈性模量Ec=34.5 GPa，泊松比νc=0.2；鋼腹桿彈性模量Es=206 GPa，泊松比νs=0.3。

圖2 組合箱梁縱立面圖（單位：cm）

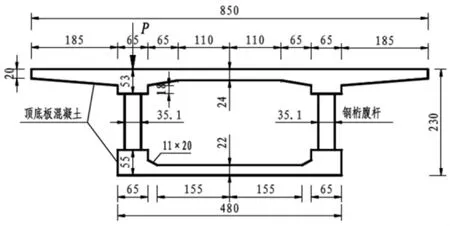
圖3 組合箱梁橫截面圖（單位：cm）

4.2 約束扭轉剪應力計算

根據前文推導的公式，得到鋼腹桿的縱向表觀彈性模量Ex=0.014 4Es，橫截面計算簡圖如圖4所示，并在橫截面上布置5個測點。

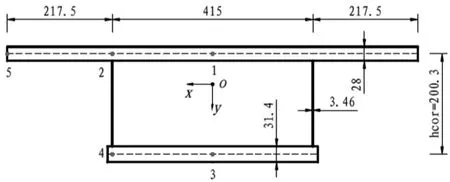
圖4 等效箱梁計算簡圖（單位：cm）

根據扭轉特性的計算方法[12]，求得扭轉中心位于頂板中點下方0.455 9 m處，廣義主扇形坐標如圖5所示，進一步求得組合箱梁其余各項截面特征參數，見表1。

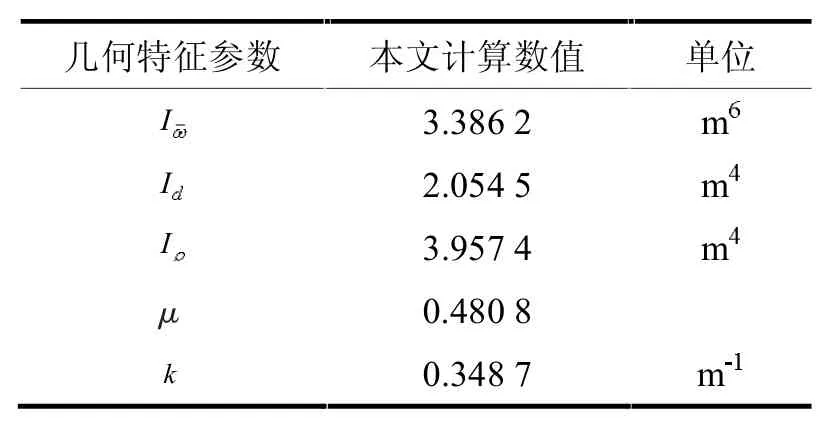
表1 扭轉幾何特征參數

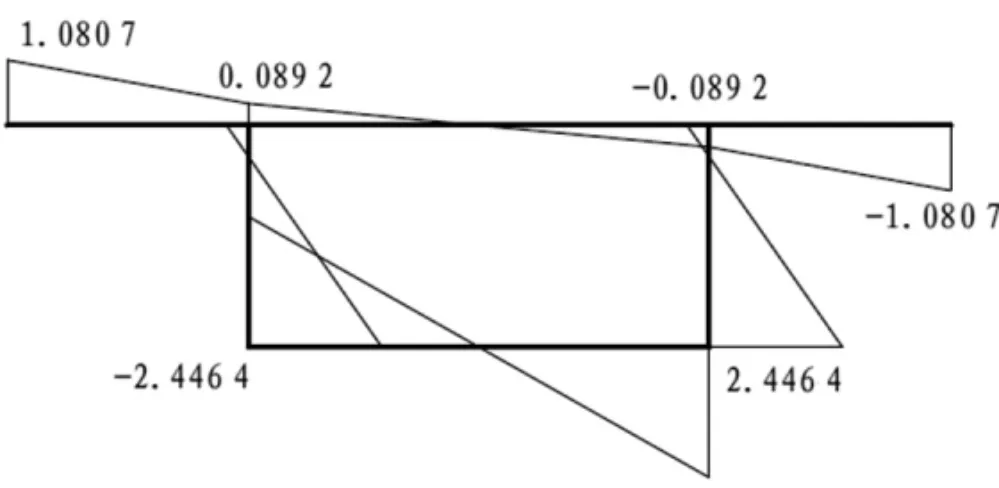
圖5 廣義主扇形坐標圖（單位：m2）

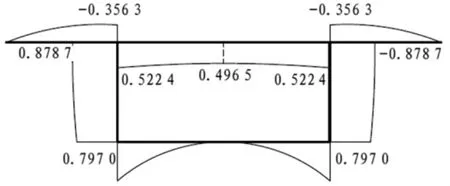
圖6 扇形靜矩圖（單位：m4）

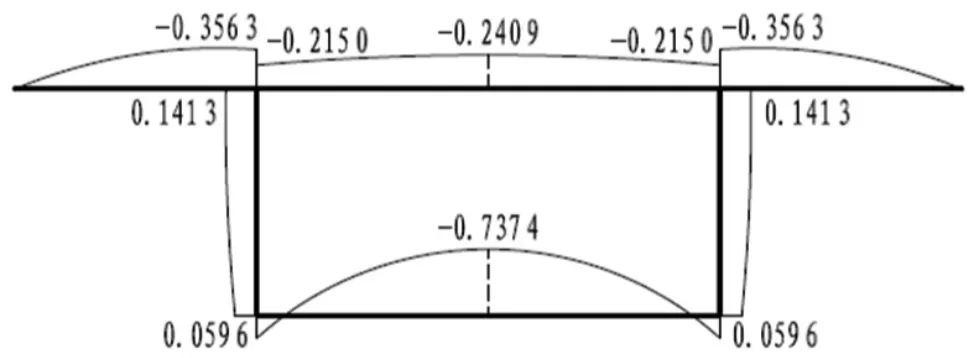
圖7 廣義扇形靜矩圖（單位：m4）

根據初參數法求解出跨中截面的自由扭矩和彎扭力矩分別為：

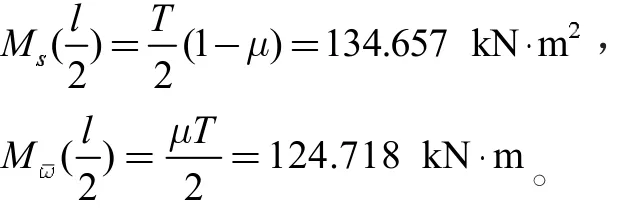
代入以上幾何特征參數求得組合箱梁跨中截面的約束扭轉剪應力，如圖8所示。由圖8可知，約束扭轉剪應力在換算鋼腹板上最大，其次為混凝土底板中心處，從底板中心處向底板與腹桿交點處靠近應力值逐漸減小；混凝土頂板上的剪應力值較小；頂板懸臂端處剪應力為0，這是由于懸臂板屬于開口部分，開口部分不涉及自由扭轉剪應力，而懸臂自由端不受約束，所以翹曲剪應力也為0，故頂板懸臂端處約束扭轉剪應力為0，隨著計算點逐漸向懸臂板內部靠近，剪應力數值逐漸增大并達到峰值，完全符合剪力流在懸臂部分的分布規律。

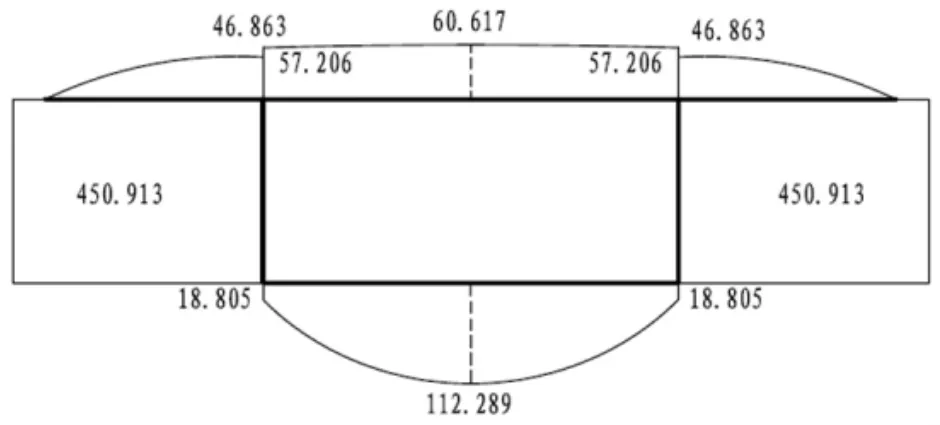
圖8 跨中截面扭轉剪應力圖（單位：kPa）

以此算例為研究對象，探究彎扭力矩隨著集中扭矩分別作用在簡支鋼桁腹-混凝土組合箱梁L/4、跨中和3L/4截面處的變化，圖9所示為彎扭力矩沿梁縱向的變化曲線。彎扭力矩在集中扭矩作用處達到最大值，并且衰減速度相當快，距離集中扭矩作用處越遠，彎扭力矩就越小，梁端處為接近為0。

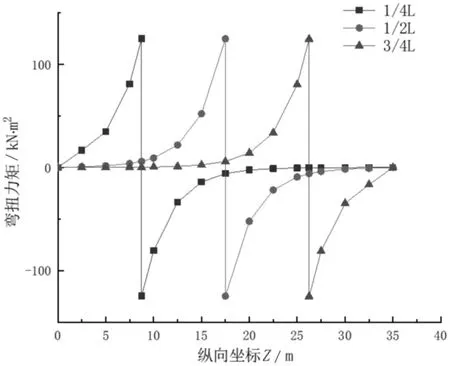
圖9 彎扭力矩沿梁長的變化曲線

通過在跨中添加集中扭矩為例，繪出1點（頂板中點）、2點（頂板與左腹桿交點）、3點（底板中點）的扭轉剪應力沿梁縱向的變化曲線，如圖10所示。在集中扭矩作用處的彎扭力矩最大，使得該處產生的扭轉剪應力最大；2點在端部的剪應力為0，是因為2點處的剪應力僅由彎扭力矩產生，而端部的彎扭力矩接近為0。

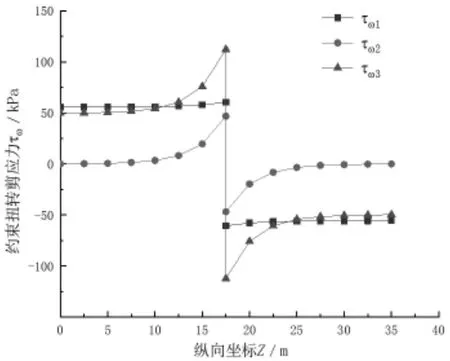
圖10 約束扭轉剪應力沿梁長的變化曲線

4.3 有限元對比分析

為驗證本文理論計算方法的可行性與準確性，利用ANSYS軟件建立有限元模型，混凝土頂底板采用三維實體單元SOLID185單元模擬，鋼腹桿采用梁單元BEAM188。端橫梁和跨中橫隔板采用SOLID185單元。不考慮鋼腹桿與混凝土的相對滑移，鋼腹桿與混凝土板連接為共節點。對于簡支鋼桁腹-混凝土組合箱梁的邊界條件為：固定鉸支座端約束UX、UY、UZ、ROTY、ROTZ，活動鉸支座端約束UX、UY、ROTY、ROTZ。在跨中頂板與腹桿交界處，施加一對大小為p/2的反對稱集中力。為減少組合箱梁在偏載作用下發生的畸變效應，在跨中位置設置了橫隔板。有限元模型如圖11所示。

圖11 有限元模型

通過有限元可求解出鋼桁腹-混凝土組合箱梁在跨中截面處1點（頂板中點）、2點（頂板與左腹桿交點）、3點（底板中點）、4點（底板與左腹桿交點）和5點（懸臂板自由端）的扭轉剪應力，與前文的理論解進行對比，見表2。

表2 約束扭轉剪應力理論數值與有限元數值對比分析

由表2可知，有限元結果與本文方法計算的理論結果較為吻合，差值百分比在10%以內，可見本文計算方法合理可行。

5 結論

（1）本文基于烏曼斯基第二理論，分析了組合箱梁剪力流的組成和分布，并推導了混凝土頂底板及換算鋼腹板兩種不同材料的約束扭轉剪應力計算公式。

（2）通過在簡支鋼桁腹-混凝土組合箱梁跨中截面作用集中扭矩為算例，分析了組合箱梁跨中橫截面上剪力流的分布規律：腹板的扭轉剪應力值最大，其次是混凝土底板中心處，由底板中心向底板與腹桿交點處逐漸減小，在混凝土頂板及懸臂板上剪應力值較小，在懸臂板自由端處為0，說明鋼腹桿對組合箱梁抗扭起著較大作用。

（3）根據算例分析了彎扭力矩和約束扭轉剪應力隨梁長方向的變化規律，彎扭力矩在集中扭矩作用處達到最大值，并且衰減速度很快，梁端處接近為零；約束扭轉剪應力也在集中扭矩作用處達到最大值。

（4）通過建立有限元模型并施加反對稱集中荷載，利用本文方法計算扭轉剪應力理論值與有限元值進行比較，結果表明本文理論計算數值與有限元數值的差值百分比在10%以內，可見本文推導的理論計算方法合理可行。