基于ARIMA-SVR的福建省入境游客人數預測

江雨兮

（上海理工大學 中英國際學院，上海 200000）

隨著人們生活水平的提高，旅游業得到高速發展。為了優化配置旅游行業的市場和資源，精確預測旅游人數，把握旅游業發展趨勢是有必要的[1]。

目前，我國旅游市場趨勢的預測研究主要采用定量分析的方法來預測旅游業的發展趨勢。國內學者關于旅游業發展研究的文獻分析，對旅游客流量的研究大多是從時間或空間的角度進行的[2]。主要使用方法是傳統的統計模型，如引力模型[3]，灰色模型[4]。

從國際研究的角度看，國外旅游業發展趨勢的研究主要集中在定量分析統計數據上，再與定性方法相結合來預測。在人工智能模型得到廣泛應用之前，主要用傳統的回歸模型預測旅游業的發展趨勢；如運用時間序列、神經網絡、計量經濟模型等方法對旅游業發展趨勢的預測[5-6]。隨著近年來先進技術的飛速發展，越來越多的研究集中在具有更高預測精度的測量技術上[7-8]。模型逐漸由單一化向多樣化發展。Wong等[9]對香港入境游客分別采用ARIMA、ADLM、ECM和VAR四種不同的單一模型以及三種不同方法的組合模型（平均分配權重法；方差——協方差法；折現均方預測誤差法）進行預測，比較指標，獲得組合模型對于預測旅游人數具有較高的預測精度的結論。

一般來說，無論在國內還是國外，由于旅游市場本身是一個復雜的系統，具有許多不確定的、不可控的影響因素，僅僅使用單一模型來預測難以取得較為精確的預測結果。因此國內外學者開始嘗試將模型組合的預測方法，使用新的組合模型來提高預測的精度。而在此之前還未有人對福建省入境游客人數變化趨勢進行研究。游客人數數據的動態性和非線性性，該數據是非平穩的、復雜的難以預測的時間序列。因此，本文考慮將ARIMA模型與SVR模型組合來預測，將通過ARIMA-SVR組合模型分析研究福建省入境游客人數的變化趨勢，對線性預測模型與非線性預測模型的關系進行探討。

1 研究方法

本文收集了福建省1979-2020年的旅游人數數據。主要采用ARIMA模型以及SVR模型分別研究福建省入境游客人數變化趨勢的線性、非線性部分。接著將線性建模結果與非線性預測得到的殘差相結合，得到的結果即采用ARIMA-SVR模型預測的福建省入境游客人數。最后在與對比模型的比對下，通過判斷模型預測評價指標的大小，得出ARIMA-SVR組合模型能夠更為精確地預測福建省入境游客人數變化趨勢。

2 ARIMA和SVR模型特點

2.1 ARIMA模型

ARIMA（Autoregressive Integrated Moving Average）模型，是一種常見的時間序列預測模型。其特點：只要由內生變量進行構造，簡單易于實現；在ARIMA模型用于時間序列時，要求序列必須是平穩的。如果序列不平穩，則必須多次微分將其平穩化。多階整體也就是通過多次微分變換的非平穩時間序列；ARIMA模型能勾勒出時序數據的大局線性趨勢。ARIMA模型對非穩定的數據以及數據非線性部分無法精確擬合。ARIMA（p，d，q），p、q被稱為自回歸項的滯后階數和移動平均項的滯后階數，差分時間序列使其平穩化所造成的次數用d表示。ARIMA（p，d，q）被稱為差分自回歸移動平均模型[10]。

2.2 SVR模型

SVR（Support Vector Regression）算法是常用的機器學習算法且模型性能優秀。它最早由Vapnik教授在20世紀90年代時提出。隨著計算機技術的發展，支持向量機模型得到了快速的發展和廣泛的應用。支持向量機的算法原理是確定特定的核函數（kernel）使得特征空間能夠得到擴展，使得樣本進行線性可分性的分析；對于線性不可分割的情況，要使用線性算法處理樣本的非線性特征，最終使得樣本在高維特征空間中能實現線性可分[11]。SVR模型的特點：僅用部分支持向量來做超平面的決策，無需依賴全部數據；對缺失數據較敏感；可以使用多種多樣的核函數靈活解決非線性回歸問題，對于小樣本有很好的預測精度，泛化能力強。

3 ARIMA-SVR模型原理

本文將采用如下步驟構建組合模型來進行福建省入境游客人數的預測。

（1）輸入1979-2012年數據作為ARIMA模型的訓練集，構建ARIMA模型對線性部分進行分析，假設預測結果為根據2013-2018年的測試集數據得出序列的殘差為Nt，Nt中容納了序列Yt的非線性關系；

（2）通過重構前一步得到的序列Nt得到SVR樣本集，并利用SVR模型預測殘差以得到預測結果

由于ARIMA和SVR的單一模型各有不同的優點和缺點，但在解決線性模型和非線性模型的問題時，兩者具有不同的優點。因此，這兩種模型是相輔相成的。因此，為了預測旅游人數可以將兩個結合起來得到精度更高的結果。假設線性自相關部分Lt與非線性殘差Nt兩個部分被看作時間序列Yt的組合，用公式表示就是Yt=Lt+Nt。利用組合后的ARIMA-SVR組合模型來期望得到預測精度更優的結果。

組合預測原理如圖1所示：

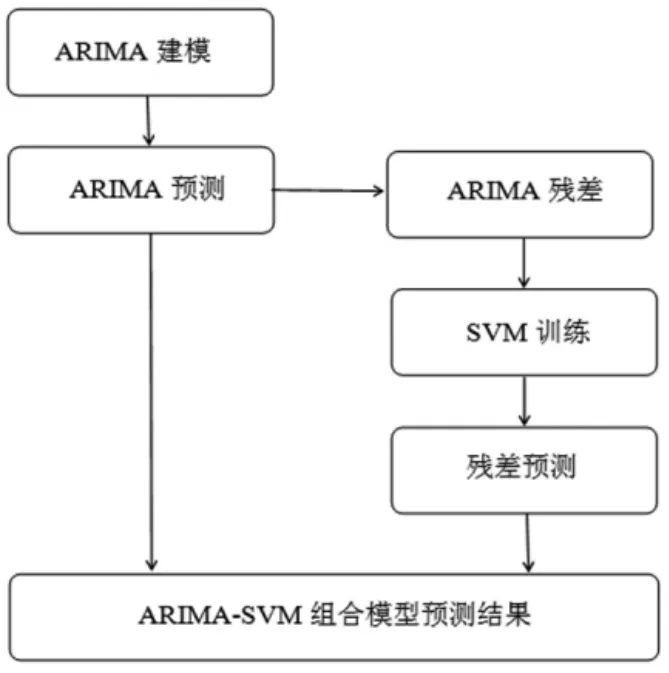
圖1 ARIMA-SVR組合預測模型原理

4 ARIMA-SVR模型的福建省入境游客人數預測

4.1 數據來源

本文從福建省統計年鑒中獲取1979-2020年的福建省入境游客人數的年度數據，共42條記錄，數據真實可靠，見表1。

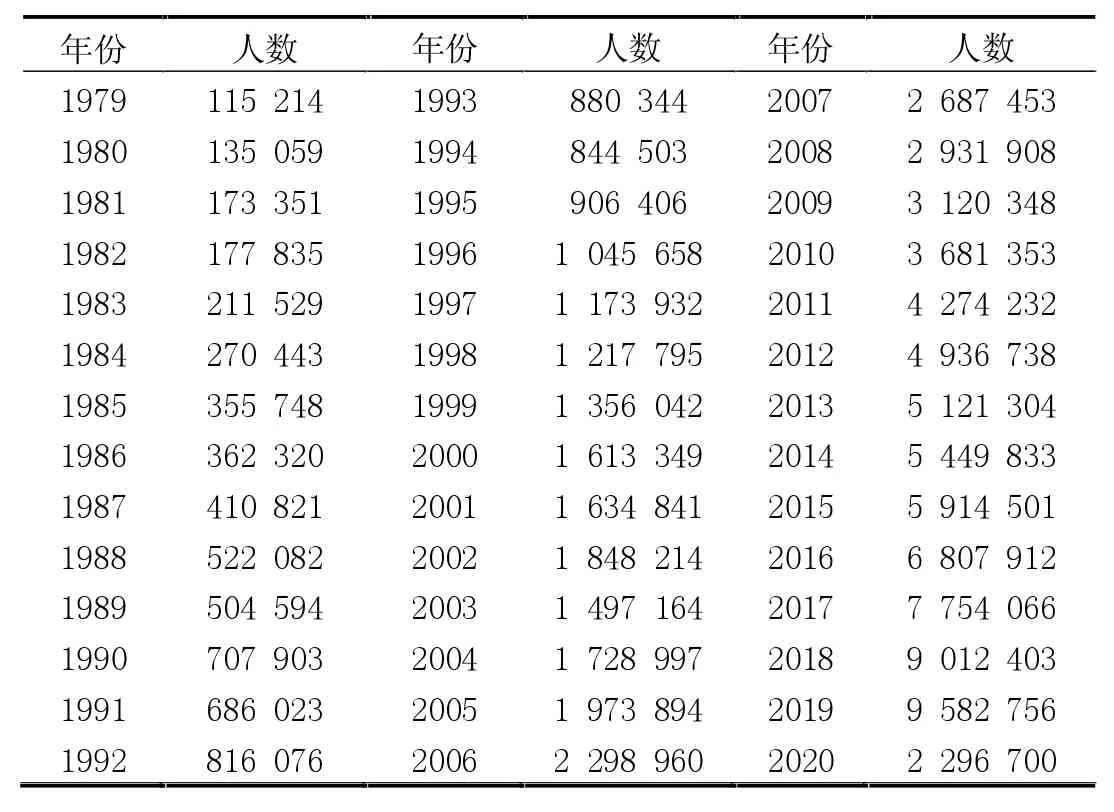
表1 1979-2020年福建省入境旅游人數表

在數據處理方面，將1979-2020年福建省入境游客人數時間序列繪制成時序圖，如圖2所示。通過繪圖展示，我們可以初步從1979-2019年從福建省入境游客人數數據中看出序列是否有著明顯的長期增長的趨勢。除2020年新冠疫情的出現，導致福建省入境游客數量急劇減少。

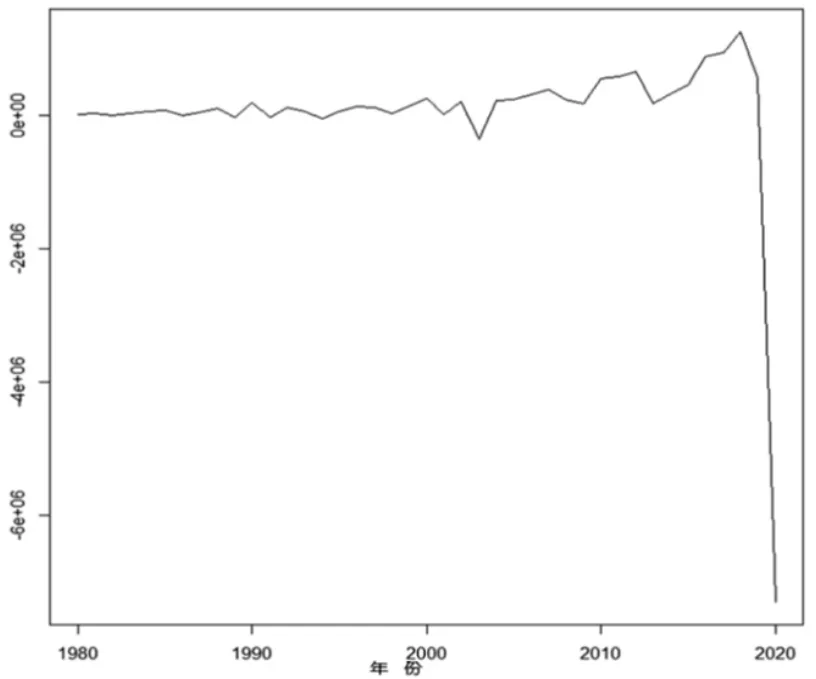
圖2 1979-2020年福建省入境游客人數時序圖

4.2 ARIMA-SVR模型預測結果

福建省入境游客人數容易受到各種因素的影響使用單一模型來預測福建省入境游客人數的變化趨勢可能是困難的，并且在預測精度方面，也難以達到預期的效果。因此，在單一模型預測精度不高的情況下，我們采用ARIMA-SVR組合模型對福建省入境游客人數進行預測。

我們能夠清晰地從圖2的時間序列圖中看出，福建省的旅游人數有長期的增長趨勢，因此我們需要對福建省入境游客人數時間序列做差分運算。一階差分后的序列也能明顯顯示出了長期的增長趨勢。

如圖3所示，福建省入境游客人數時間序列經過一階差分后的時間序列呈現出長期的穩定性，基本上在0附近波動上下均勻波動。

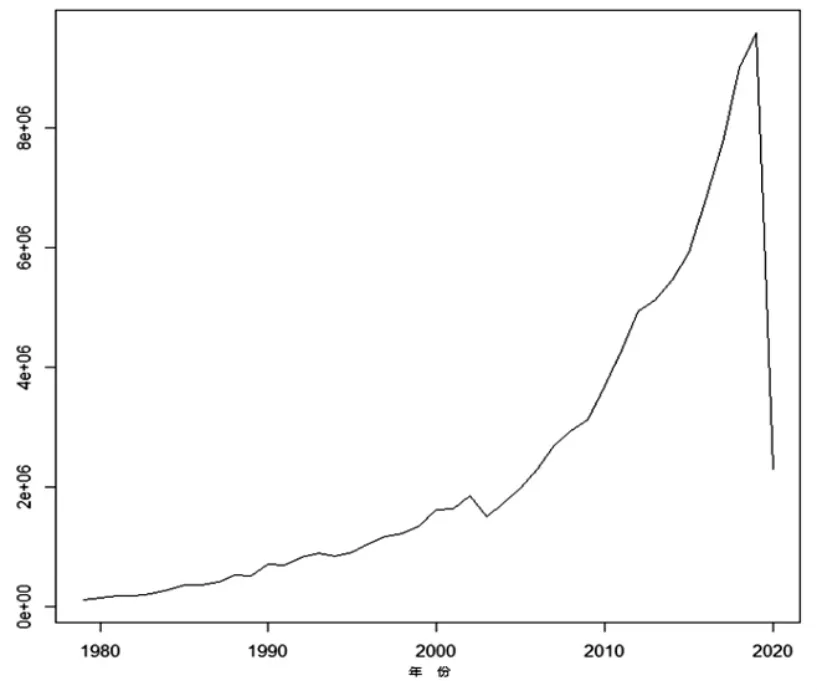
圖3 福建省入境游客人數一階差分時序圖

為了更準確地描述數據穩定性，可以使用ADF檢驗單位根來進行檢驗是否平穩。若序列是平穩的，則可以直接用ARIMA模型來擬合，反之則要經過差分轉換。ADF單位根檢驗結果見表2。

表2 福建省入境游客人數二階差分的單位根檢驗結果

我們可以從ADF檢驗看出，序列的p值等于0.021 8，p值小于顯著性水平α（α=0.05），以上計算結果表明，單位根檢驗結果顯著，一階差分后的序列不存在單位根，所以我們可以說一階差分序列是穩定的。為了更加準確地確定模型的階數，我們利用AIC準則，通過AIC值來說明模型擬合度越高。分別計算各模型的AIC值，結果可知ARIMA（1，1，1）的AICc值最小，可以求出ARIMA（0，1，1）的AIC值、AICc值以及BIC值分別為1 266.11、252.71以及255.07。再對ARIMA（0，1，1）模型進行檢驗擬合得出模型參數的顯著性，結果見表3。

表3 模型參數的顯著性檢驗結果

最后將所得的ARIMA（1，1，1）模型進行參數的顯著性檢驗。檢驗結果顯示，估計出的系數除以其的標準差（s.e.）得到的商的絕對值大于1.96，落入拒絕域，拒絕原假設。因此，沒有必要重新修正所建立的模型。最后選持的時間序列模型為ARIMA（1，1，1）模型。

現在我們利用所建立的ARIMA（1，1，1）模型對2013-2020年福建省全年的旅游人數進行預測，結果如圖4所示。

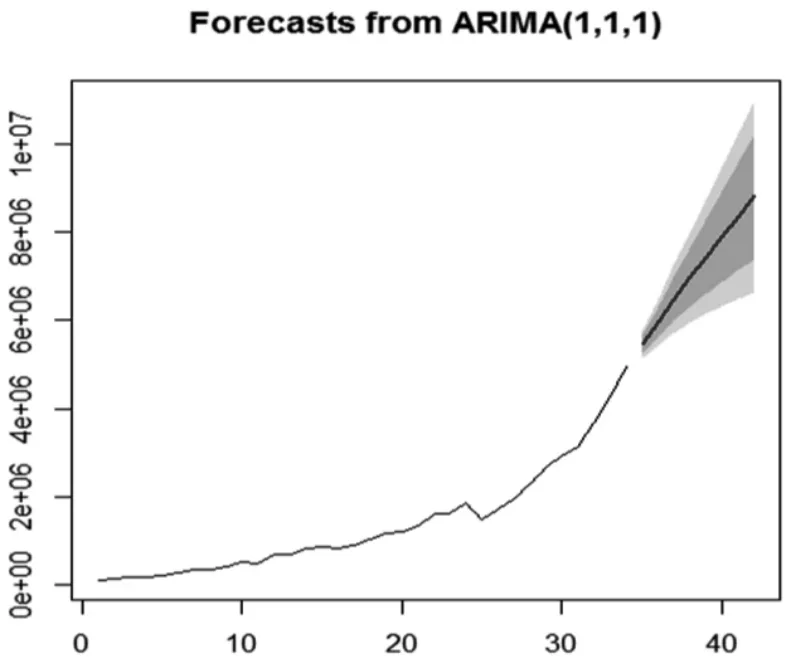
圖4 2013-2020年福建省入境游客人數ARIMA模型預測

利用模型預測值與測試集比較求出誤差，分析 模型的均方根誤差、平均絕對誤差、平均百分比誤差等幾個用來衡量精度指標，來進行對比分析模型的預測精度，見表4。

由表4得知，模型預測值與實際值的誤差較小，平均百分比誤差為2.269 8。模型的平均絕對百分比誤差值為9.601、平均絕對比例誤差為0.653。表明ARIMA（1，1，1）模型擬合的效果較為良好，精度滿足要求。

表4 評價預測精度指標

然而，由于福建省入境游客客流量受到國家政策、經濟形勢、突發事件等因素的影響，要想利用單一的ARIMA模型進行長期的、絕對準確的預測較為困難。因此我們仍需對該模型進行一些改進。

為了選擇一個最優個數能夠使得循環殘差數據的誤差最小，我們采用第N次選擇N個殘差數據，保留誤差為它的第N+1個殘差數據作為模型輸出的方法。所以最優個數定為4時能讓模型循環殘差的誤差最小。

通過模型選定的最優循環殘差個數，可以得出結論，福建省入境游客人數的殘差與前4年旅游人數的殘差高度相關。在R軟件中調用e1071程輯包來實現SVR建模，核函數為高斯核函數。參數采用十折交叉驗證獲得，通過擇優選擇懲罰系數C=10 000以及gamma=0.000 01，作為最優參數來對2016-2020年福建省入境游客人數殘差進行預測。

表5 基于ARIMA-SVR福建省入境游客人數預測結果

4.3 對比模型

為了引入對比模型，我們分別采用單一的SVR模型以及ARIMA模型對福建省入境游客人數進行了預測分析。利用滑動窗口對SVR模型進行訓練，訓練集為1979-2016年福建省入境游客人數序列x（t）。

運用通過訓練集構建好的SVR模型和ARIMA模型對2017-2020年的福建省入境游客人數進行預測，得出來的預測結果與測試集，即2017-2020年實際數據做比較，計算得出誤差，結果如圖5和表6所示。通過折線圖和誤差表比對，我們可以清晰地看出，單個ARIMA和SVR模型在短期預測可能得到更精確地效果。但是ARIMA-SVR組合預測模型在較為長期預測中，能夠結合ARIMA模型在求解線性問題以及SVR模型在解決非線性問題上的優勢。使得預測出來的結果具有更高的預測精度和更小的誤差。

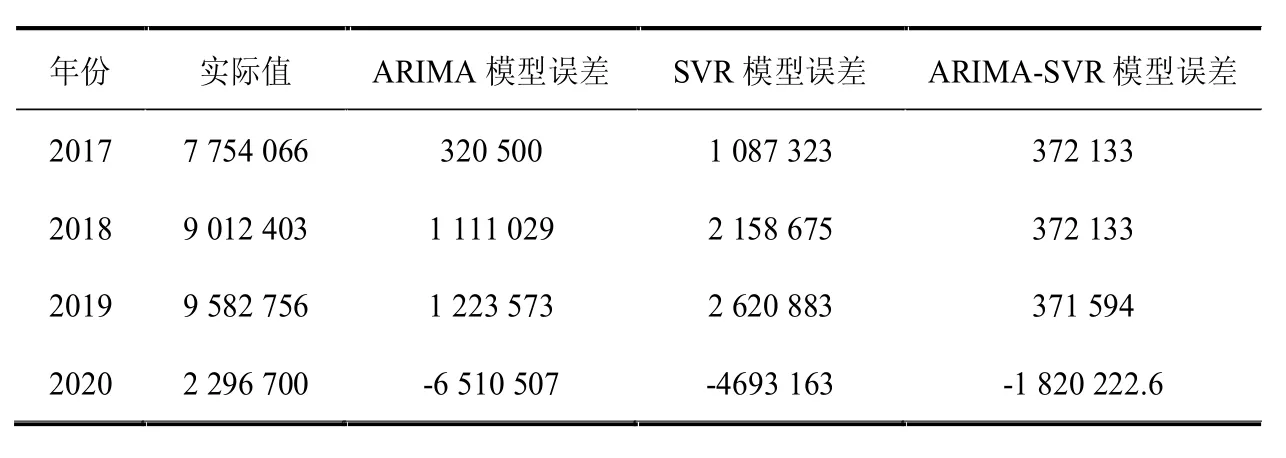
表6 2017-2020年3個模型預測誤差對比

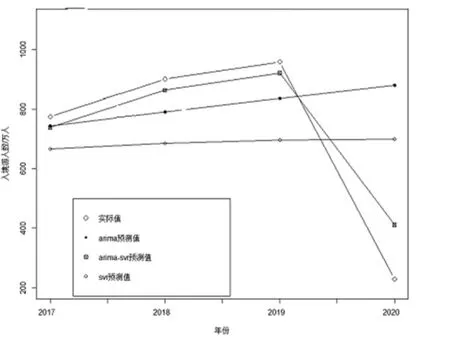
圖5 2017-2020年3個模型預測折線圖對比

這表明雖然單一模型短期預測比較有優勢，但對于解決復雜且不穩定的時間序列問題，它們都必定不是最優模型。而本文使用的ARIMA-SVR組合模型分別結合了ARIMA模型和SVR模型各自獨有的優點，使得預測精度有效地提高，預測誤差大幅度減小。

4.4 ARIMA-SVR模型預測福建省入境游客人數

根據模型精度評價可以得出，相比與單個的ARIMA和SVR模型，我們所建立的更高精度、誤差更小的ARIMA-SVR組合預測模型，克服了單一模型只能對序列線性或者非線性部分進行預測的弊端，更能充分地捕捉已知福建省入境游客人數數據中隱含的信息，從而來預測未來幾年的數據。因此我們利用ARIMA-SVR組合模型以及1979-2020年福建省入境游客人數序列來預測每年的旅游人數。

從實際數據可以看到，2019、2020兩年間，福建省入境游客人數仍在趨增，兩年間福建省入境游客人數將增長到每年千萬人次級別，分別為9 194 023、5 815 290人次，結果說明ARIMA-SVR組合模型預測的數據具有一定的科學性和一定的參考意義。能夠為有關部門及早地、準確地制定旅游規劃，優化旅游市場資源配置提供依據。

5 結束語

經濟的高速發展使得旅游業大力興起，隨著福建省頒布一系列促進旅游業發展的政策，福建省入境游客人數將必將呈現出持續增長的趨勢。雖然游客數量的增加給景區帶來了豐厚的利潤，但也不可避免地帶來了一連串的交通、安全、服務質量問題，和疫情防控方面的高度要求，從而導致旅游服務質量急劇下降，市場趨于混亂。針對上述問題，本文對福建省入境游客人數進行預測，綜合過去的信息，并使用定性和定量的方法來揭示旅游人數數據的變化趨勢，以便為社會和經濟發展提供判斷的方向，提前制定相應的政策來促進社會的穩定發展。

然而，在現實生活中福建省入境游客人口的波動規律與其他數據不同，包含數據之間的線性關系以及其非線性特征。因此以往單一的預測方法存在一定的限制，不能很好地滿足我們所需求的預測精度。組合預測的方法能夠較好地吸取單一模型的特點，互補模型之間的不足，基于這一點我們選擇使用ARIMA-SVR組合模型來預測福建省入境游客人數的變化趨勢，此模型較好地結合了單一模型各有的優勢，構建ARIMA模型處理福建省入境游客人數的線性趨勢，SVR模型預測福建省入境游客人數變化的非線性規律。最后引入對比模型，根據對比模型精度結果表明，該組合模型相比于單一模型能夠提高預測的準確性，準確把握福建省入境游客人數的變化趨勢，并且比單一模型更合理、更可靠，可作為一種有效的工具用于福建省入境游客人數時間序列的預測。