具阻尼廣義Korteweg-de Vries 方程的迭代學(xué)習(xí)控制*

明 森，李 霞，范雄梅

（1.中北大學(xué)數(shù)學(xué)系，太原 030051；2.中北大學(xué)大數(shù)據(jù)學(xué)院，太原 030051）

0 引言

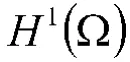
經(jīng)典的KdV 方程描述淺水中小振幅長(zhǎng)波的單向運(yùn)動(dòng)，是一類分布參數(shù)系統(tǒng)，即

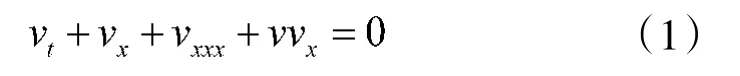
其中，v（t，x）是水波的高度。在現(xiàn)實(shí)情形，耗散效應(yīng)和非線性色散效應(yīng)對(duì)物理系統(tǒng)的影響同樣很重要。文獻(xiàn)［12］研究了一類具阻尼的廣義KdV 方程。

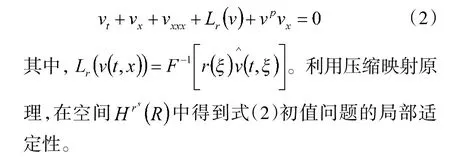
考慮到耗散效應(yīng)的影響，本文研究一類具阻尼廣義KdV 方程的控制問(wèn)題。

本文擬采用P 型學(xué)習(xí)律設(shè)計(jì)出迭代學(xué)習(xí)控制器，給出此分布參數(shù)系統(tǒng)迭代學(xué)習(xí)控制算法收斂的充分條件及數(shù)值實(shí)例。

1 預(yù)備知識(shí)

2 局部適定性

本節(jié)給出式（3）的局部適定性定理及證明。

證明 主要利用引理1～引理4 及文獻(xiàn)［12］給出定理1 的證明。利用半群理論，對(duì)于式（3），有

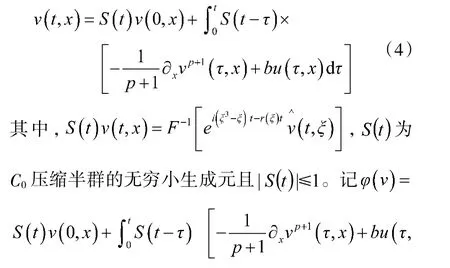
3 迭代學(xué)習(xí)收斂性分析

對(duì)于式（3），采用P 型迭代學(xué)習(xí)控制算法

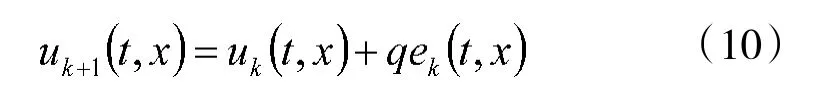
其中，k 表示迭代次數(shù)，q＞0 是待尋的學(xué)習(xí)增益。假設(shè)在迭代過(guò)程中系統(tǒng)的初始狀態(tài)允許存在一定的誤差，即

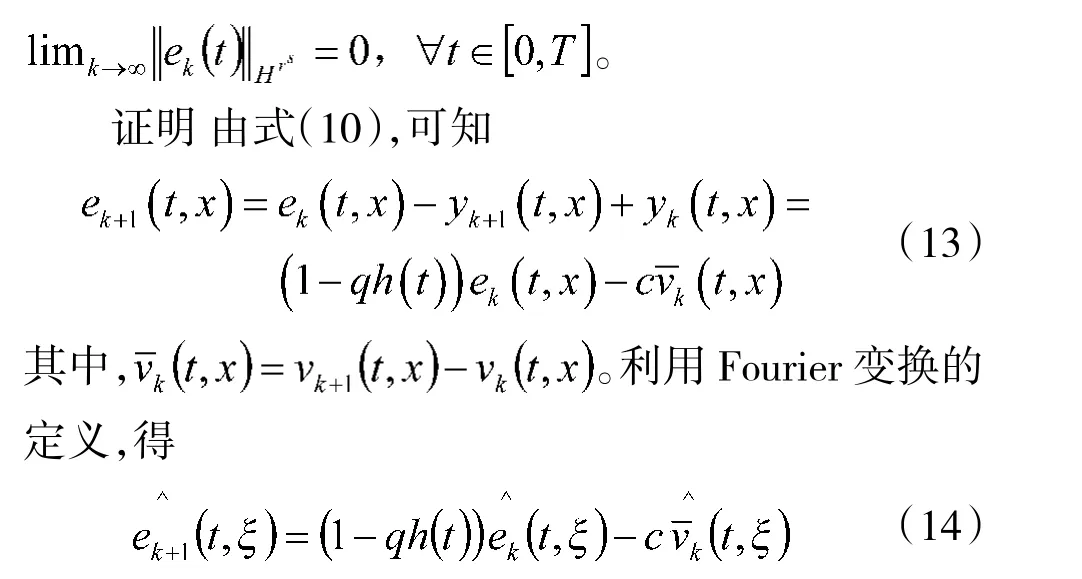
利用半群理論及式（3），得

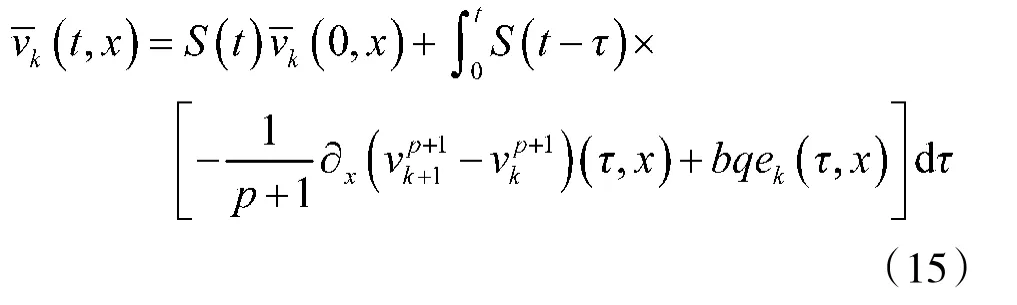
因此

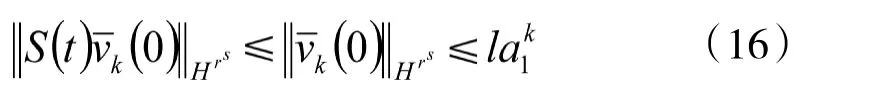
利用引理4，得到

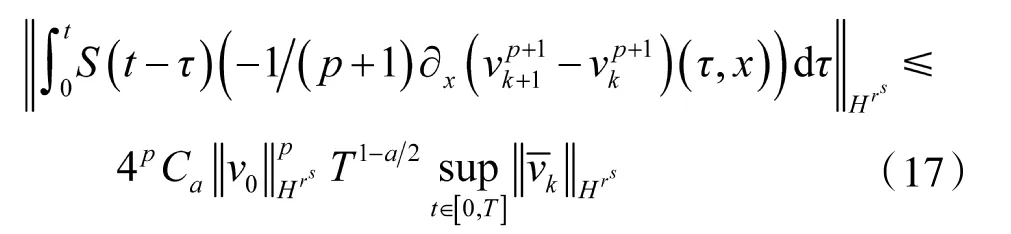
及

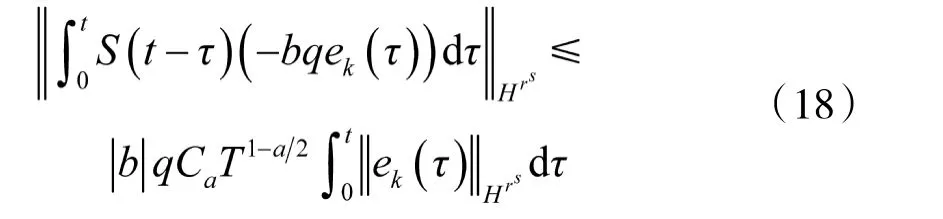
由式（15）和式（16），可知

4 數(shù)值實(shí)例

從而說(shuō)明可選取適當(dāng)?shù)膆（t）與ε，進(jìn)而得到相對(duì)應(yīng)的學(xué)習(xí)增益q。

5 結(jié)論