葉輪結構對浮選動力學特性的影響

唐 軍 滕瑜崇 劉 輝 于明明 匡敬忠 符東成

(1.江西理工大學機電工程學院,江西 贛州 341000;2.贛南科技學院,江西 贛州 341000;3.江西理工大學資源與環境工程學院,江西 贛州 341000)

自吸式浮選機的循環量與葉輪結構參數存在耦合關系[1],循環量過大,會使分離液面不穩定,影響礦化泡沫的收集,循環量過小,礦物難以充分懸浮,會降低礦化泡沫的產量。因此,通過優化浮選機的葉輪結構,在合理范圍內提高循環量,有助于提高礦物回收率。CFD作為一種有效的研究方法和技術手段,廣泛應用于浮選機研究領域[2-3]。周原彬等[4]通過CFD分析了單相流下葉片傾角對流場特征和浮選機循環量的影響,發現葉片傾角對液相的軸向速度、湍動能和壓力差有較大影響,葉輪傾角為徑向(0°)時有助于提高浮選機循環量。LIU Baoqing等[5]采用CFD研究了礦物入料位置、入料離散數等對礦物懸浮性的影響,并在相同工況下,分析了新式雙葉片葉輪較傳統葉輪在提高礦物懸浮均勻性方面的優勢。GUNWANTM[6]利用CFD模擬了攪拌桶內部流體的運動特征,根據模擬結果,提出了循環體積的計算方法,同時分析了葉輪傾角對攪拌桶功耗的影響,發現后傾葉輪可以降低攪拌桶的功耗。AMEUR H[7]借助CFD探究了葉輪個數、輪盤間隙對流體粒子分布特征的影響,以提高流體粒子的懸浮性為目標,確定了最佳葉輪個數和輪盤間隙。孟麗等[8]設計了一種隔板葉輪,采用CFD研究了氣-液兩相流下,隔板葉輪對浮選機性能的影響,并通過試驗對模擬結果進行了驗證,得出隔板葉輪與原有葉輪性能相當。

上述研究主要模擬了浮選機內部的流體動力學特性,其成果對浮選機的優化具有借鑒意義,但對葉輪的優化研究大部分僅停留在傾角等基本參數上,導致自吸式浮選機葉輪形式單一,性能提升不明顯。因此,本文以提高自吸式浮選機循環量、礦物懸浮均勻性為目標,將循環量更強的雙倒錐臺式結構與星型徑向葉輪進行了結合。借助CFD方法及試驗驗證,對比分析了優化前后葉輪對浮選動力學特性的影響。

1 結構模型與仿真方法

1.1 結構模型建立與網格劃分

JJF-0.2 m3試驗樣機主要由豎筒、分散罩、定子、葉輪、循環筒、假底、罐體等結構組成,結構示意圖見圖1,采用SolidWorks對其建立的物理模型見圖2。葉輪作為自吸式浮選機最主要的結構兼具吸氣和循環礦漿的作用[9],試驗樣機原用星型徑向葉輪見圖3,結合理論研究及工程實踐經驗,對原有葉輪進行優化后形成的改進葉輪見圖4。

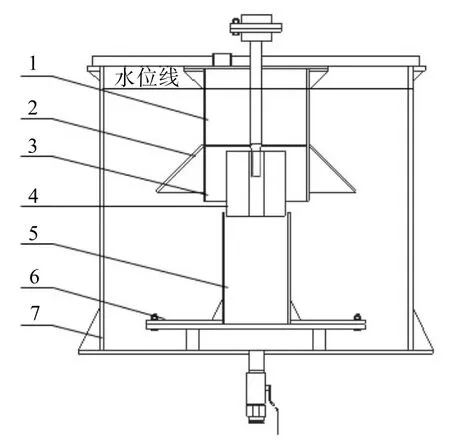
圖1 JJF-0.2m3試驗樣機結構示意Fig.1 The schematic diagram of JJF-0.2m3 test prototype structure

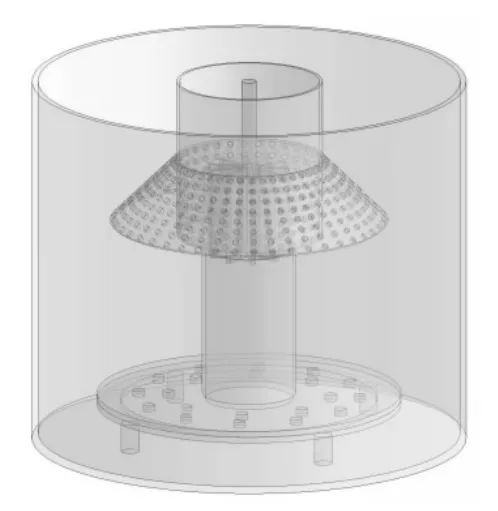
圖2 JJF-0.2 m3試驗樣機物理模型Fig.2 Physical model of JJF-0.2 m 3 test prototype

圖3 星型徑向葉輪Fig.3 Star radial impeller

圖4 改進葉輪Fig.4 Improved impeller

在Ansys Fluent軟件中對JJF物理模型進行流體域的填充,以及靜止域和旋轉域的拆分后,通過Mesh生成非結構化網格。為提高仿真結果的可靠性,在定子、分散罩、假底等多孔位置進行局部網格加密處理,網格無關性的檢驗選取單相流下循環筒內某一點液相的流速變化趨勢作為評判標準,網格無關性檢驗見表1。由表1可知,隨網格數量增加,液相流速趨于穩定,在網格數量大于9.61×106后,液相流速的波動范圍相較于前一套網格在6%以內,綜合考慮模擬結果的可靠性及計算成本,最終選取網格數量為9.61×106。

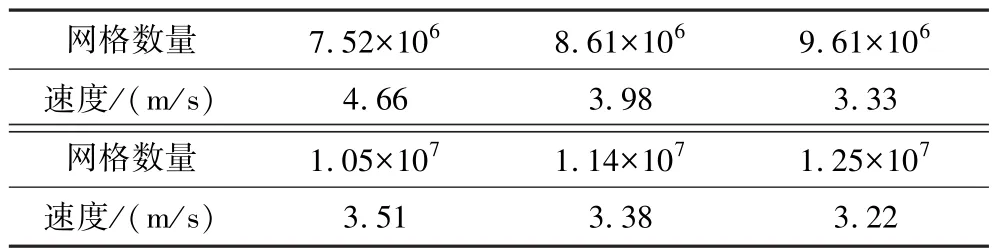
表1 網格無關性檢驗Table 1 Grid independence test table

1.2 仿真模型選擇與條件設置

Standardk-εModel模型作為最常用的湍流模型[10],在浮選機的模擬研究中已被證實了具有良好的預測能力,因此單相流采用Standardk-εModel模型,其中湍動能k和耗散率ε的輸運方程為:

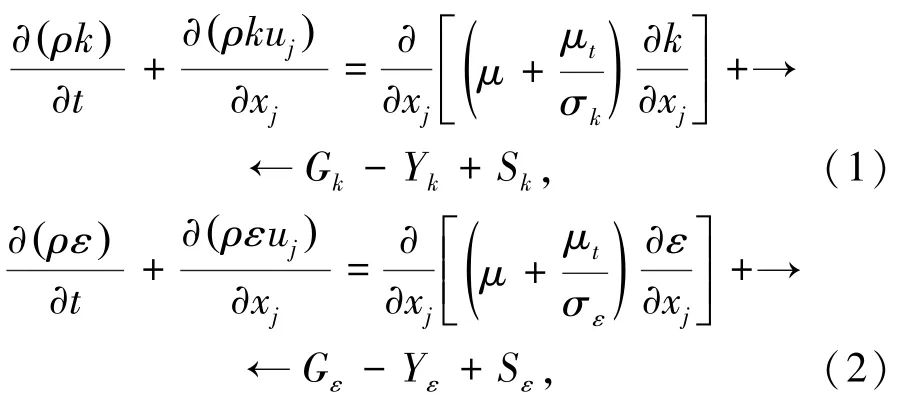
式中,Yk和Yε分別代表湍動生成的k和ε;Sk和Sε為自定義源項;Gk為平均速度產生的湍流動能,m2/s2;Gε為湍動產生的湍流動能,m2/s2;σk和σε分別為k和ε的湍動普朗特數。

不考慮氣相時,利用歐拉-歐拉方法,對采用Standardk-εModel湍流模型的固-液兩相流進行模擬計算。曳力模型采用Gidaspow,其中固相懸浮和運動的主要動力來源為液相對其的曳力,計算過程中忽略升力、附加質量力等小量級力。浮選中固相顆粒被處理為與液相相互作用的連續介質時,固相間的固相應力采用顆粒動力學理論模型來描述。葉輪高速旋轉時固相顆粒不發生變形,每一相的運動由連續性方程和動量守恒方程控制[11],兩種方程分別為:

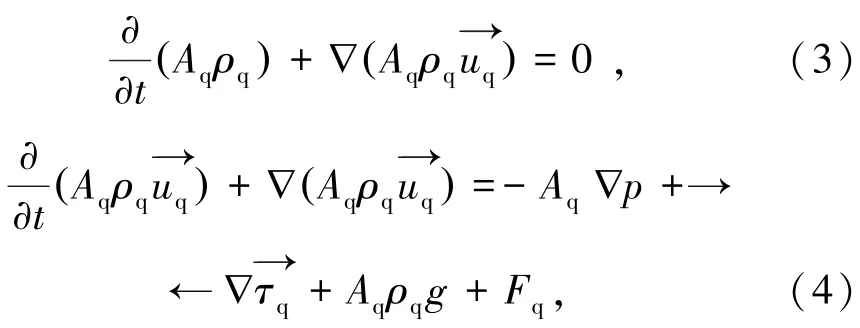
式中,Aq為第 q相的礦漿體積分數;ρq為密度,kg/m3;為速度,m/s;p為壓強,Pa;為應力張量,Pa;g為重力加速度,m/s2;Fq為相間作用力,N。

罐體內壁設為光滑壁面,液相和固相分別設為No silp和Free slip邊界條件[12]。固相為黃銅礦,液相為清水,固相、液相的基本參數設置見表2,所有模擬案例的葉輪轉速均為997 r/min,并采用穩態求解,數值計算終止基于平方根殘差為1×10-5的可靠性收斂準則。

表2 固相、液相的基本參數Table 2 Basic parameters of solid and liquid phases

2 試驗結果分析

2.1 葉輪結構對流場特征的影響分析

單相流模擬下,兩種葉輪旋轉時浮選機罐體內液相的速度矢量圖見圖5。

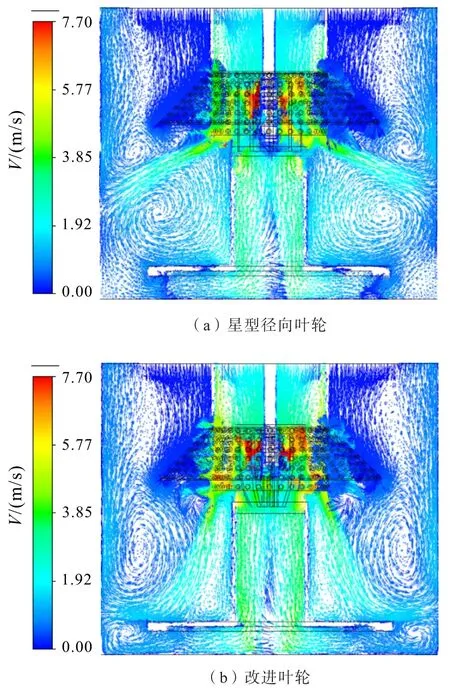
圖5 液相速度矢量圖Fig.5 Liquid phase velocity vector diagram

從圖5可以看出,兩種葉輪旋轉時罐體內部均形成上下兩個大的對稱循環渦流,其中上部流場主要為礦物顆粒和氣泡的碰撞以及運輸礦化泡沫創造適宜的流場條件;下部流場旨在為未參與循環的礦物顆粒提供循環機會。在浮選過程中,葉輪甩出的礦漿無法完全由定子孔排出,部分未排出的礦漿在葉輪攪拌下沿豎筒內壁運動,形成一個有利于浮選機卷吸空氣[13]的局部循環渦流。相較于傳統星型徑向葉輪,改進葉輪旋轉時能夠在罐體底部形成兩個較小的循環渦流,同時提高循環筒內液相的軸向流速。其中,罐體底部小渦流的存在可以提高礦物顆粒的懸浮性,循環筒內較高的軸向流速能夠提高浮選機循環量。

2.2 葉輪結構對湍流特性的影響分析

流場分析只能定性地對液相流動趨勢進行描述,無法詳細說明流場的紊亂特征,而湍流動能是速度脈沖值的體現,可以定量描述流場的湍流特性[4]。單相流模擬下,兩種葉輪旋轉時浮選機罐體內的湍流動能分布見圖6。

由圖6可知,兩種葉輪旋轉時均在豎筒和循環筒內形成了湍流,并且湍動能最大值都出現在葉輪處,相較于星型徑向葉輪,改進葉輪旋轉時在豎筒和循環筒內形成的湍動能分布范圍更廣、強度更高,有助于提高浮選機的吸氣量和循環量。

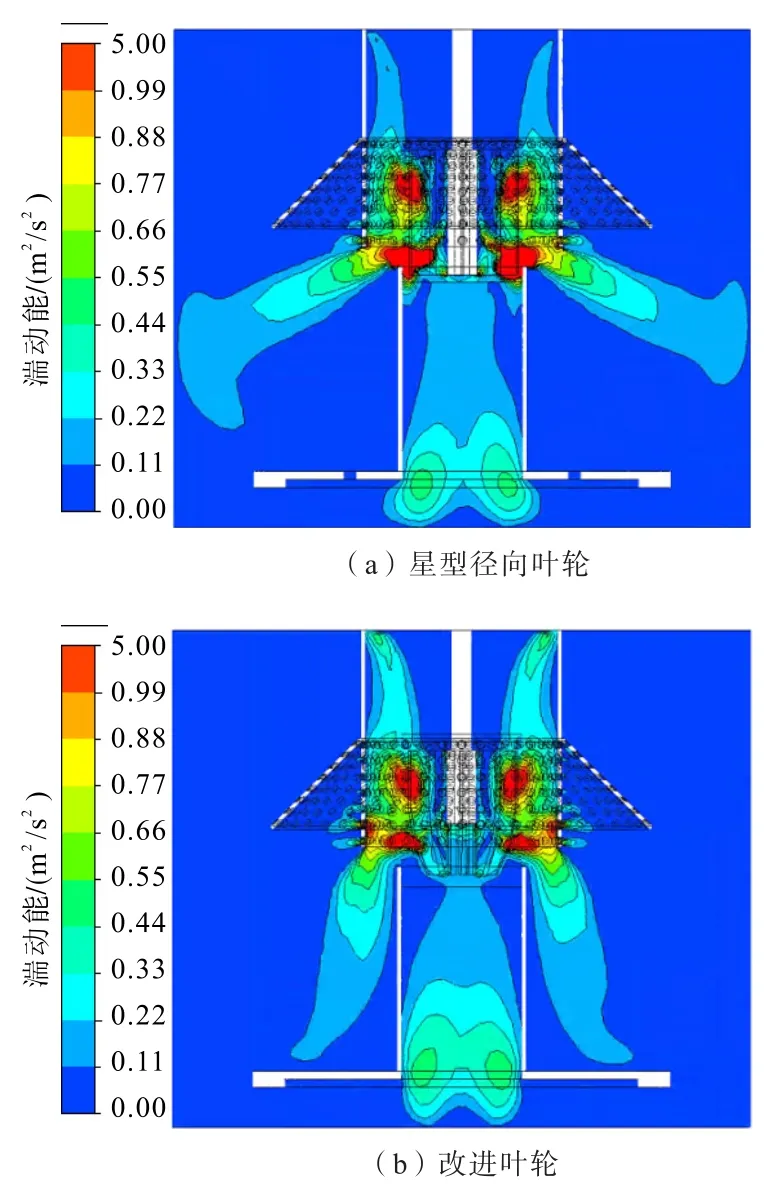
圖6 湍流動能分布Fig.6 Turbulent kinetic energy distribution map

2.3 葉輪結構對模擬循環量和功耗的影響分析

為研究葉輪結構對模擬循環量和功耗的影響,分別提取兩種葉輪在單相流下和固相粒度為50μm的兩相流下的模擬性能參數。因循環量是根據循環筒內液相的軸向流速進行計算的[6],故通過CFD-POST后處理軟件,提取距離罐體底部0.08 m處循環筒截面上液相的平均軸向流速,采用速度-面積法計算得出模擬循環量。扭矩利用葉輪所受液相的扭力與作用半徑的積分計算后,帶入公式獲得模擬功耗。兩種葉輪的模擬性能參數見表3。

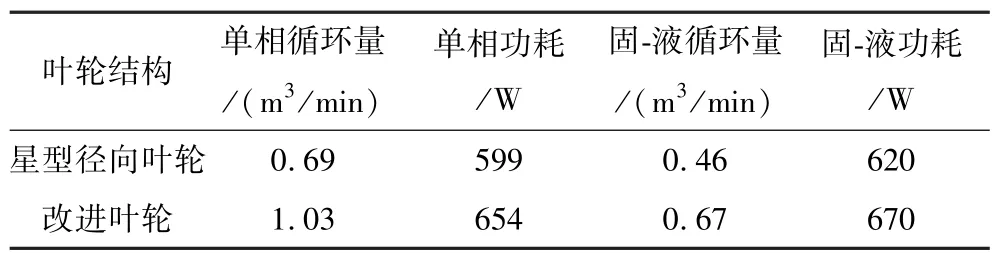
表3 2種葉輪的模擬性能參數Table 3 Simulation performance parameters of two impellers

從表3可以看出,兩種葉輪在單相流下的循環量模擬值均大于固-液兩相流下的模擬值。結果表明,固相的參與降低了循環量、增大了功耗,符合實際情況,也從側面驗證了仿真結果的可靠性。

通過對比兩種葉輪的模擬性能參數,發現改進葉輪對浮選機循環量提升顯著,相較于星型徑向葉輪,改進葉輪的循環量在單相流模擬下提高了49%,兩相流模擬下提高了46%;功耗在單相流模擬下增大了9%,兩相流模擬下增大了8%。

2.4 葉輪性能參數的試驗研究

在給料粒度為45～55μm(平均粒度50μm)、體積濃度為10%的黃銅礦礦漿中,對兩種葉輪的整體性能參數進行對比研究。由于試驗樣機體積小,測量循環筒內礦漿軸向流速不現實,故采用在假底底面邊沿r=0.52 m的圓周上布置10個速度測量點,通過獲取速度測量點徑向流速的平均值,來等效循環筒內礦漿的平均軸向流速,進而計算出礦漿循環量。礦漿流速的測量采用便攜式測算儀(圖7),功耗的測量采用扭矩傳感器(圖8),吸氣量采用排水集氣法進行測量得出。為降低偶然因素對葉輪性能參數測量的影響,分別對轉速為997 r/min時的礦漿流速、功耗、吸氣量進行3次測量,最終通過取平均值的方法計算出葉輪的各性能參數。兩種葉輪的試驗性能參數見表4。

圖7 便攜式測算儀Fig.7 Portable vibration meter

圖8 扭矩傳感器Fig.8 Torque transducer

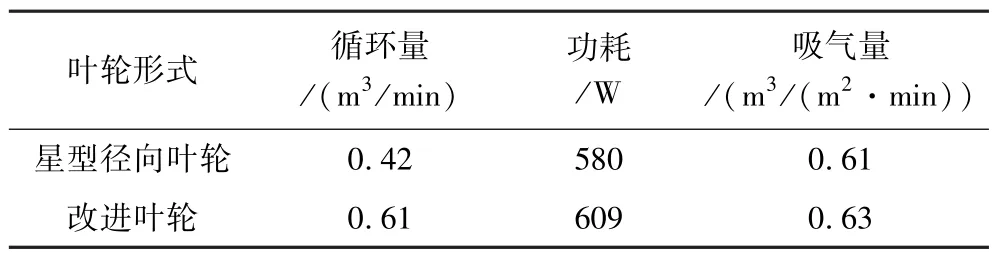
表4 2種葉輪的試驗性能參數Table 4 Test performance parameters of two impellers

從表4可以看出,在轉速為997 r/min時,改進葉輪相較于星型徑向葉輪礦漿循環量提高了45%,功耗增大了5%,吸氣量提高了3%。研究發現,浮選機循環量與其容積比的范圍在3～5之間時浮選效果最佳[14],在該比值范圍內,提高循環量可以降低發生礦漿短路的概率,提高礦化泡沫的產量。改進葉輪旋轉時浮選機循環量與其容積比為3.05,能夠保證礦物顆粒的懸浮時間,進而提高礦物顆粒進入葉輪區與氣泡發生再碰撞的概率。

將兩種葉輪在固-液兩相流下的模擬性能參數與試驗性能參數進行對比后發現,循環量和功耗的模擬值與試驗值的相差程度均在10%以內,造成誤差的部分原因為忽略氣相影響所致。試驗結果進一步驗證了模擬結果的可靠性以及改進葉輪優化的合理性。

2.5 粒度和葉輪結構對礦物懸浮均勻性的影響分析

粒度是影響礦物懸浮均勻性的關鍵因素之一[15],為深入研究粒度對礦物懸浮均勻性的影響,分別以給料粒度為50μm、74μm和120μm的黃銅礦作為模擬研究對象,對其進行固-液兩相流模擬,得到的礦物濃度等值線圖見圖9。

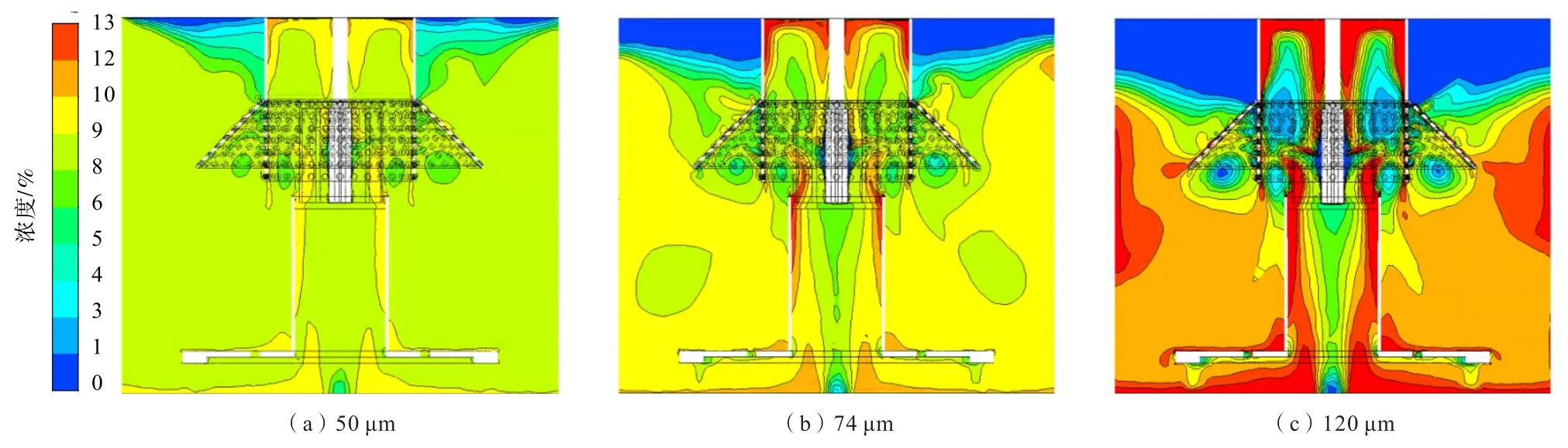
圖9 礦漿濃度等值線分布Fig.9 Isoline distribution of mineral concentration

從圖9可以看出,粒度為50μm的礦物顆粒在液相的分散程度更高,假底和罐體底部無明顯礦物堆積現象;粒度為74μm的礦物顆粒在罐體底部開始出現礦物堆積現象,分散程度適中;粒度為120μm的礦物顆粒分散程度最差,在靠近分離液面很長一段距離無礦物顆粒分布,大量礦物堆積在假底和罐體底部。

因罐體內礦物的分布特征具有對稱性,故選取距離葉輪軸線中心r=0.26 m,長度為0.62 m的取樣范圍,并在該范圍內均勻選取30個樣本點,用該范圍內礦物的懸浮均勻性來反映整個罐體內部的礦物懸浮均勻性。取樣范圍示意見圖10。

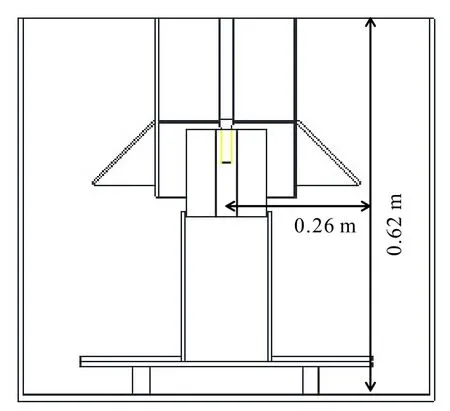
圖10 取樣范圍示意Fig.10 Sample point diagram

礦物懸浮均勻性的兩個評價指標為礦物懸浮性α和懸浮均勻度ζ,對應的計算公式分別為[16]:

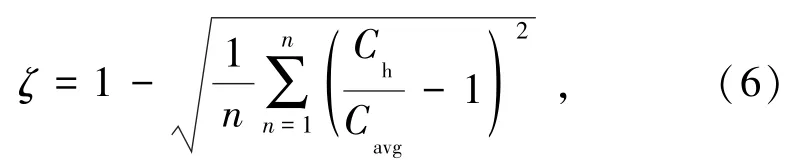
式中,Ch與Cavg分別表示取樣范圍內各樣本點的濃度值和平均濃度值,n表示樣本點個數。α和ζ與1越接近表明礦物顆粒的懸浮均勻性越好。

根據懸浮性α的計算公式,計算給料粒度分別為50μm、74μm和120μm的黃銅礦在取樣范圍內的α值,得出的給料粒度對礦物懸浮性的影響曲線見圖11。

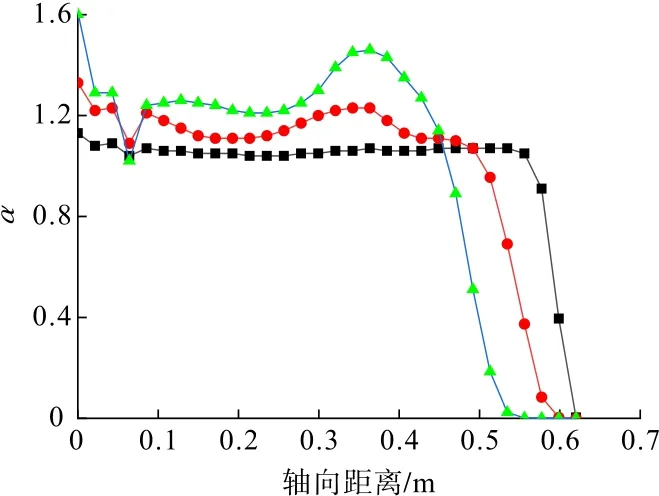
圖11 粒度對礦物懸浮性的影響Fig.11 Influence of particle size on mineral suspension

從圖11可以看出,粒度越大礦物顆粒越不易懸浮,罐體底部礦物濃度明顯增大,導致該點α值與1的間距變大。粒度為50μm的礦物懸浮性曲線近似于直線與1最貼近,在靠近分離液面時曲線急劇下滑;粒度為120μm的礦物懸浮性曲線波動最大且在更低位置出現曲線急劇下滑現象;粒度為74μm的礦物懸浮性曲線介于50μm和120μm的礦物懸浮性曲線之間,分布較為平緩。粒度為50μm、74μm和120μm的礦物ζ值分別為0.95、0.81和0.68,綜合礦物懸浮均勻性的兩個評價指標可以得出,隨粒度增大礦物懸浮均勻性變差。

為研究葉輪結構對礦物懸浮均勻性的影響,在選取粒度為120μm的黃銅礦作為模擬對象,固-液兩相流模擬下,兩種葉輪旋轉時罐體內的礦物濃度等值線圖見圖12。從圖中可以看出,星型徑向葉輪旋轉時礦物在液相的分散程度較弱,礦物在罐體底部和假底上方堆積嚴重。由于改進葉輪抽吸效果顯著,罐體底部礦物濃度較小,礦物的整體分散程度較高,但假底和循環筒的夾角處仍有少量礦物堆積。

圖12 礦漿濃度等值線分布Fig.12 Isoline distribution of mineral concentration

葉輪結構對礦物懸浮性的影響曲線見圖13。

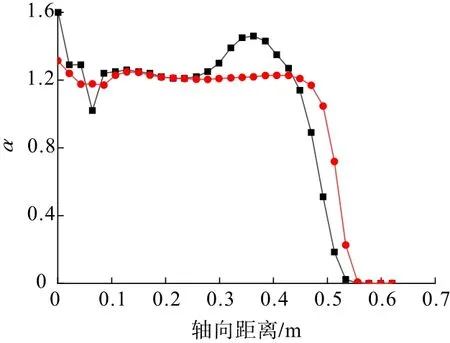
圖13 葉輪結構對礦物懸浮性的影響Fig.13 Influence of impeller structure on mineral suspension

由圖13可知,相較于星型徑向葉輪,改進葉輪旋轉時礦物懸浮性曲線更加平緩且α值與1更貼近,曲線急劇下滑現象出現在相對較高位置。星型徑向葉輪和改進葉輪旋轉時粒度為120μm的礦物ζ值分別為0.68和0.75。綜合礦物懸浮均勻性的兩個評價指標可以得出,改進葉輪在提高礦物懸浮均勻性方面效果顯著。

3 結 論

(1)通過結合理論研究及工程實踐經驗,對JJF試驗樣機原有葉輪進行優化后形成了一種能提高浮選機循環量及礦物懸浮均勻性的改進葉輪,通過CFD模擬和試驗研究,驗證了改進葉輪優化的合理性。

(2)研究表明,相較于星型徑向葉輪,改進葉輪旋轉時在豎筒和循環筒內形成了更強的湍動能,浮選機循環量顯著提升,功耗略微增大,吸氣量無明顯變化。粒度對礦物懸浮均勻性有較大影響,隨粒度增大,礦物在液相的懸浮均勻性變差,改進葉輪在提高礦物懸浮均勻性和解決礦物沉槽問題方面效果顯著。

(3)改進葉輪提高了罐體內礦物的懸浮均勻性,但假底和循環筒的夾角處仍有少量礦物堆積,除控制礦物粒度和優化葉輪結構外,對夾角處的結構進行優化也是提高礦物懸浮均勻性的一種方法。