基于直觀想象的“全等三角形的復習課”教學思考

陳黎雨

關鍵詞：直觀想象;對稱性;全等三角形

一、培養直觀想象能力的重要性

培養學生的直觀想象能力，是數學學科核心素養落地的重要標志之一。直觀想象是發現和提出問題、分析和解決問題的重要手段，是探索和形成論證思路、進行數學推理、構建抽象結構的思維基礎。

直觀想象是指借助幾何直觀和空間想象感知事物的形態與變化，利用空間形式特別是圖形，理解和解決數學問題的素養。主要包括：借助空間形式認識事物的位置關系、形態變化與運動規律;利用圖形描述、分析數學問題;建立形與數的聯系，構建數學問題的直觀模型，探索解決問題的思路。[1]

只有學生具有了良好的直觀想象能力，并且將這種能力遷移到所有領域的問題解決過程中，其他五個核心素養的落地才更具有可行性。[2]

二、培養直觀想象能力的方法

直觀想象能力的培養離不開訓練學生識圖構圖的思維方式，看問題的角度決定了學生是否能夠發現和提出問題。在新課程標準中，“圖形與幾何”的設置包含了三個專題：“圖形的性質”、“圖形的變化”、“圖形與坐標”，平時教學中，學生對于基本圖形性質中的“元素之間的關系”與“對稱性”的學習較為割裂，學生在復雜的圖形中難以區分基本圖形，根據圖形的變化想象構造圖形并探索解決問題的方向，因此教師應在日常教學中從“圖形的變化”的角度引導學生觀察基本圖形，進一步理解“圖形的性質”，再從“圖形的性質”解釋“圖形的變化”，相互融合，最后總結模型，從而促進學生能夠主動運用基本圖形的對稱性分析問題，能通過直觀想象猜想、構造圖形并探索解決問題的方向.

在組織具體教學的過程中，可以選擇“全等三角形的復習課”等課程，以“角”是一個軸對稱圖形為切入點，將“圖形的變化”和“圖形的性質”融合在教學過程始終。

（一）從“圖形的變化”的角度想象基本圖形

學生的直觀想象能力的提升并不是一蹴而就的，需要在幾何學的課程上培養數學思維方式，識圖的方向是很重要的一步，要做到有向有序地識圖、分析圖，這與教師的在最開始的幾何學看圖的思維方式有很重要地關聯，主要是從“圖形的對稱性”的角度識圖，觀察圖形與圖形之間的位置關系、大小關系，然后再觀察元素與元素之間的位置關系、大小關系。

“幾何作圖”是一個好的載體，作圖過程中能分析“圖形元素之間的關系”，對培養直觀想象能力中的識圖構圖起著重要的作用。

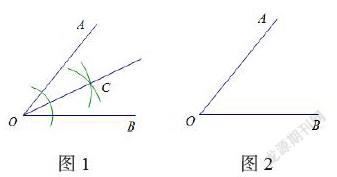
例如：全等三角形的復習課中，如圖1，若點C是銳角∠AOB內一點，分別在射線OA和射線OB上確定點E，F，使得△OCE≌△OCF，用尺規確定點C，E，F的位置并說明理由。

直觀想象能力首先是對圖形有直觀的感受，通過畫示意圖先引導學生觀察圖形，借助位置關系、大小關系看圖形的變化，然后再合理想象圖形。畫完示意圖后引導學生觀察這兩個三角形△OCE和△OCF的位置關系，觀察出共邊的全等三角形可以折疊得到，再結合“角是軸對稱圖形”想象點C的位置，并不是一個固定的點，而是點的集合，在∠AOB的平分線上，如圖2。

2.基本“圖形的變化”對三角形進行分類討論

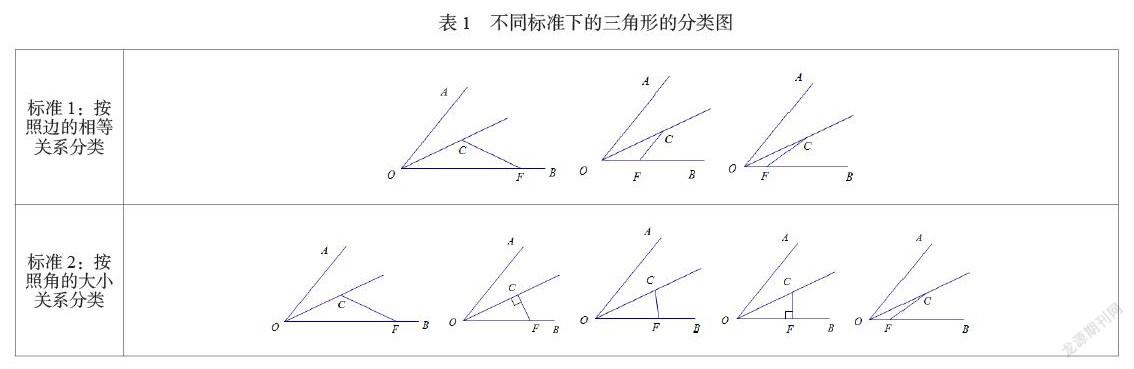
引導學生想象折疊前后的兩個三角形會構成什么圖形，也就是△OCF沿OC折疊后的△OCE與△OCF會構成什么圖形，而這與△OCF的大小和形狀有關。由于點F是在射線OB上的動點，△OCF的大小和形狀也是不確定的，因此需要進行分類討論，引導學生根據不同的標準進行討論，并畫出相應的圖形。

標準1：按照邊的相等關系分類，結合圖形可以得到三邊都不相等的三角形、等腰三角形;

標準2：按照角的大小關系分類，結合圖形可以得到鈍角三角形、直角三角形、銳角三角形如下表1.

引導學生根據條件△OCE≌△OCF思考這兩個三角形的元素關系，不難看出點E和F是一對對應點，通過追問學生如何在圖形上體現對應點引導他們將對應點轉化為對應線段或者對應角思考，這樣學生的思維也就發散開了。

從對應線段來看，可以通過思考OE和OF的關系，不難想到利用圓規分別在OA和OB上截取兩條相等的線段就可以確定點E和F的位置，如圖3， 再追問學生這樣畫法下的兩個三角形全等的依據，這樣也就復習了全等三角形的其中一種判定方法SAS. 還可以通過思考CE和CF的關系，學生會想到以及類比截取OA=OB的方法，以點C為圓心，適當的半徑畫弧，分別交OA，OB于點E，F，如圖4. 再引導觀察圖形，判斷這種畫法中點E的位置是否是唯一確定的，如果是，說明判定方法，如果不是，則說明點E的位置還可以在哪里，畫出圖形如圖5. 說明此種畫法中線段CE和CF的位置關系并不是對應的，也可以說明SSA不能證明兩個三角形全等。

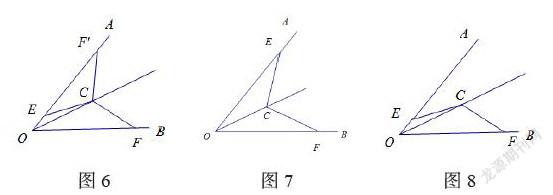
復習了全等三角形的判定后，可利用“角具有對稱性”，可用變式題目引導學生從圖形變化的角度來構圖，例如：如圖6，已知OC是∠AOB的平分線，，與之間有怎樣的數量關系？引導學生將△OCE沿OC翻折得到如圖7，或者將△OCF沿OC翻折得到如圖8，探究解題方向后從而有向有序地解決問題。

（三）從“圖形的變化”的角度總結模型

具有特殊位置關系的兩個全等三角形需要引導學生從圖形的變化的角度來識圖構圖，更重要的是需要進行總結，逐步構建基本圖形群以加深學生對基本圖形的理解，從而促進學生能夠主動運用基本圖形分析問題，探求解決問題的方向，最終提升學生的直觀想象能力。

綜上所述，學生直觀想象能力的培養與學生的全面發展有著密不可分的關系。在倡導核素理念下，讓學生有向有序地分析幾何圖形需做到引導學生根據“圖形的變化”理解“圖形的性質”，根據“圖形的性質”解釋“圖形的變化”，將幾何學的三個專題互相融合，最后總結幾何模型，因為在幾何教學中，如果能經常借助特殊模型，讓學生直觀感知特殊模型中點、線、面的位置關系，積累圖形的表象，增強直觀感，養成由直觀到想象的思維習慣，則對培養學生的直觀想象能力有明顯的促進作用[]。

參考文獻：

[1] 中華人民共和國教育部制定.普通高中數學課程標準（2017年版）. 北京：人民教育出版社， 2018

[2] 許彬城. 基于直觀想象素養培養管窺核心素養培育[J]. 數學教學通訊， 2020， 02： 32-33

[3] 徐德同，樊向陽. 例談初中生直觀想象能力的培養[J]. 教育研究與評論（中學教育教學）， 2019， 08： 10-13