庫水水位下降對平頂水庫邊坡穩定性的影響

趙 飛

(遵義水利水電勘測設計研究院，貴州 遵義 563000)

1 概 述

庫水水位下降對邊坡穩定具有重要的影響，水庫蓄水改變了水庫邊坡的內部環境，而水位的升降會導致土體內部孔隙水的流動，進而影響庫岸邊坡的穩定性能。

許多專家學者對于庫岸邊坡穩定性進行了研究，并取得了豐碩的研究成果。劉磊等[1]建立了降雨滲透模型，分析了不同降雨強度及降雨時長下坡體的穩定性；江強強等[2]結合模型試驗分析了降雨與水位升降耦合作用下，對三峽水庫庫岸邊坡的滑動特性進行研究；董金玉等[3]采用現場試驗的分析方法得到水電站庫區的邊坡力學參數，結合FLAC 3D數值分析模型分析了水庫水位升降對邊坡失穩破壞的影響機理；吳瓊等[4]利用理論分析的研究方法，分析了在降雨與水位升降作用下，庫岸邊坡坡體的浸潤線的變化范圍；王騰飛等[5]利用理論分析與三軸壓縮試驗相結合的研究方法，分析了土體在水的作用下抗剪強度的變化特征；梁學戰等[6]通過構建模型試驗的研究方法，研究了水庫邊坡在蓄水作用下，坡體裂隙的時空變化特征；羅紅明等[7]將土水特征曲線的多項式約束優化模型與飽和-非飽和滲流數值模型相結合，分析了庫水位漲落對水庫邊坡地下滲流場的影響；莫偉偉等[8]基于水巖相互作用機理,分析了庫水漲落對滑坡巖土體的影響。

基于以上的研究成果，本文擬對平頂水庫庫岸邊坡建立三維數值分析模型，分析邊坡坡度、滲透系數、水位下降速率對坡體孔隙水壓力的影響以及庫岸邊坡穩定系數的影響。

2 模型建立

本研究以貴州省赫章縣安樂溪鄉平頂村境內的平頂水庫為研究對象，該水庫一年中水位升降幅度為30 m。針對研究對象建立FLAC數值分析模型，根據相關資料，設坡高為h時，當坡腳與左邊邊界的距離為1.5 h、坡頂與右邊邊界的距離為2.5 h、上邊界與下邊界的距離大于2 h時，建立的模型計算結果準確度較高。建立網絡模型，見圖1，模型邊界的選取為：坡頂位置、水位以上位置為滲流邊界，其余邊界為自由水頭邊界，初始狀況下的水頭高度為60 m，模擬水位下降過程采用水位均勻下降的方式。

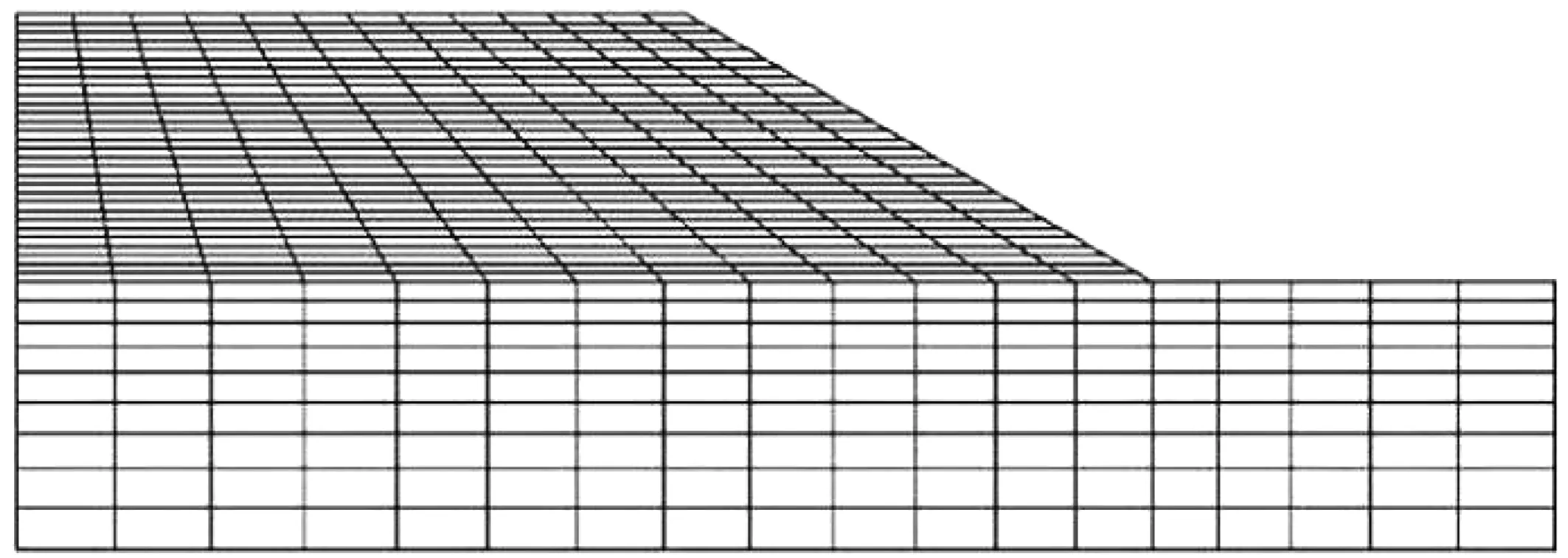
圖1 計算網格單元

根據現場測量，該庫岸邊破的滲透系數變化范圍為8.64×10-2～8.64 m/d，庫水水位下降的速率變化范圍為1～2 m/d。本研究以該庫岸邊坡的實際狀況為例，分析在不同參數條件下的邊坡穩定性，主要參數為：滲透系數分別取8.64×10-2、8.64×10-1、8.64 m/d，庫水水位下降的速率分別取1、1.5、2 m/d，庫岸邊坡坡度分別取15°、20°、30°，庫岸邊坡巖土結構的內摩擦角為23°，黏聚力為24 kPa。

3 計算結果分析

3.1 相流對邊坡穩定性計算結果的影響

邊坡坡體的相關參數取值為：滲透系數8.64 m/d，庫水水位下降速率2 m/d，庫岸邊坡坡度30°，分析兩相流與單向流作用下邊坡穩定性系數與水位下降量高度的結果，見圖2。

分析圖2中的數據可以看出，當庫水水位下降高度相同時，兩相流的計算結果比單向流計算結果稍大。這主要是由于兩相流計算模式下基質吸力不同所引起的，兩相流計算模式下，邊坡坡體內部的滲流場與孔壓場發生了變化，進而引起在上部坡體內部出現較大范圍的非飽和狀態區，在該區域內，基質吸力增大，從而該區域內抗破壞能力增強，穩定性提高，兩相流的基質吸力作用與實際更加符合。因而，本研究采用兩相流計算模式對平頂水庫邊坡穩定性進行分析。

3.2 不同工況下滲流分析

在庫水水位下降過程中，為了分析不同影響因素對平頂水庫邊坡穩定性的作用效果，將孔隙水壓力作為研究對象，設計以下3種工況進行數值模擬計算。3種工況下的參數取值見表1。

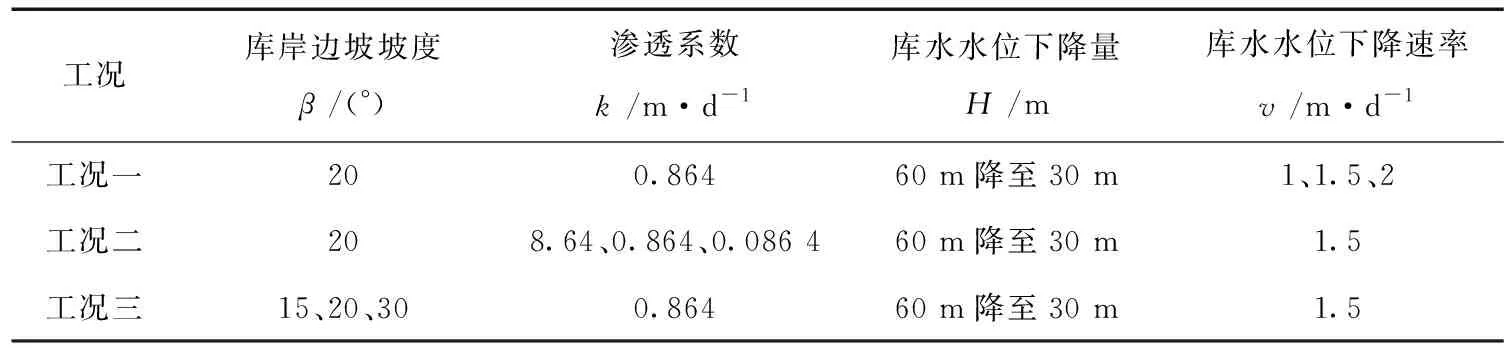
表1 不同工況下對應的參數取值

工況一的3種不同庫水水位下降速率條件下的模擬結果見圖3。在水位下降過程中，坡體外部的水壓力值降低，引起坡體內部的水壓力值大于坡體外部，水在坡體內部流動，從而改變坡體內部的孔隙水壓力。同時，由于水壓力的作用下，坡體內部逐漸由飽和狀態變為非飽和狀態，導致坡體內部出現負孔隙水壓力，對于不同庫水水位下降速率的模擬結果，在邊坡相同位置處孔隙水壓力之相差不大。因而，在合理的庫水水位下降速率調配下，對滲流作用的土體孔隙水壓力影響不大。

圖3 不同庫水水位下降速率的孔隙水壓力等值線

工況二的3種不同滲透系數條件下的模擬結果見圖4。不同滲透系數對孔隙水壓力的影響較大，當滲透系數值k=8.64 m/d時，隨著水位的下降，由于滲透系數值較大，孔隙水壓力消散較快，因而坡體內外部的孔隙水壓力值保持平均水平，孔隙水壓力值均值線未出現較大幅度的上下波動，且在坡體上部出現較大范圍的負孔隙水壓力區；當滲透系數值k=0.086 4 m/d時，隨著水位的下降，由于滲透系數值較小，坡體內的水不能及時排出，孔隙水壓力消散較慢，土體內存在較大范圍飽和區，且坡體上部負孔隙水壓力區較小。

圖4 不同滲透系數的孔隙水壓力等值線

工況三的3種不同庫岸邊坡坡度條件下的模擬結果見圖5。隨著邊坡坡度增大，庫岸邊坡底部孔隙水壓力等值線分布更加集中，同等高度水壓力差逐漸越大，因而邊坡坡度越大越有利于坡體內應力的消散。

圖5 不同邊坡坡度的孔隙水壓力等值線

4 正交試驗下不同邊坡穩定影響因素的分析

庫水水位下降會引起邊坡坡體內部滲流場出現負的孔隙水壓力，同時庫水水位下降過程中孔隙水壓力消散較慢，進而導致庫水邊坡的失穩破壞。對于常規3種影響因素的分析會產生27種組合，對于正交試驗可以有效減小組合試驗的次數，只需要進行9組試驗即可，對3種因素分為3個水平等級。見表2。

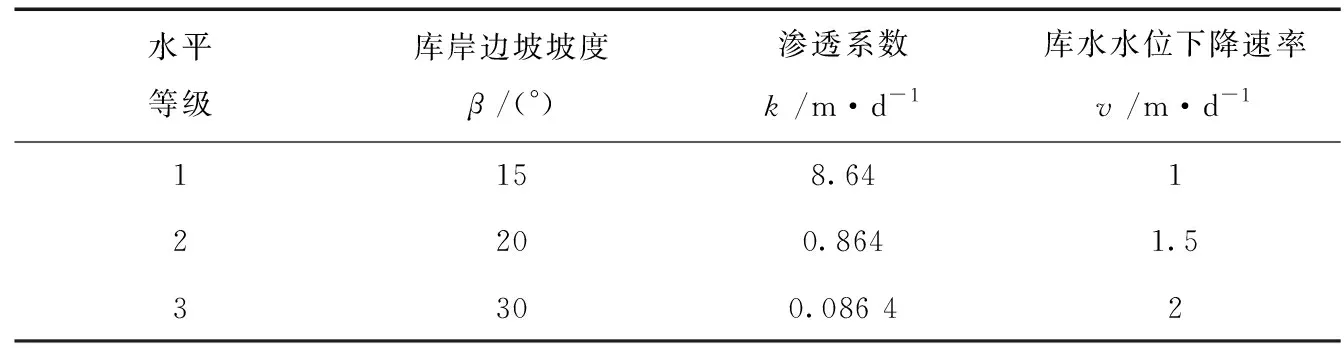
表2 因素水平分級表

將3個等級的因素進行組合得到9種組合結果，見表3。在不同種組合狀況下，平頂水庫庫岸邊坡穩定性系數隨水位下降高度變化見圖6。

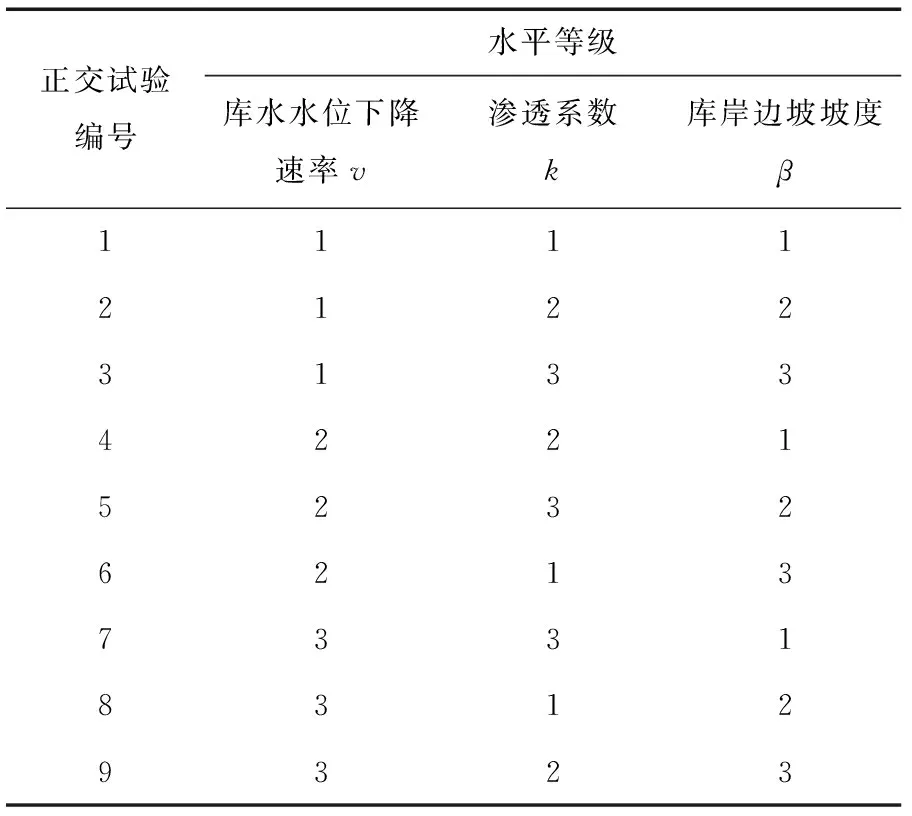
表3 正交試驗方案組合

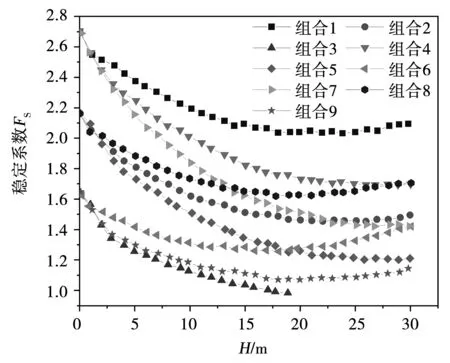
圖6 不同組合因素下的穩定系數

分析圖6，主要得到以下結果：

1) 9種因素組合下的庫岸邊坡穩定系數隨著水位高度下降均呈現先減小后增大的變化趨勢(組合3除外，由于當下降高度逐漸增大時，該因素組合下邊坡坡體出現失穩破壞)，隨著庫水水位下降，邊坡坡體穩定性系數總體上是下降的，在H=20 m左右時存在最小值。

2) 分析3種因素對庫岸邊坡穩定系數的影響，影響效果最大的是庫水水位下降的速率v。當該研究邊坡的滲透系數k和庫岸邊坡坡度β均保持不變時，隨著庫水水位下降的速率v增大，水位下降高度相同時，庫岸邊坡穩定性最差。

3) 庫岸邊坡坡度β的變化直接影響著庫岸邊坡坡體的初始應力狀態。當坡度β由15°增大至30°時，庫岸邊坡穩定系數由2.68降低至1.63，初始應力狀態的改變直接影響著滑坡體內部的穩定狀態。

4) 當初始應力狀態相同時即庫岸邊坡坡度β相同的情況下，在其他條件相同的情況下，庫岸邊坡穩定系數隨著滲透系數k的減小逐漸降低，當滲透系數k=0.086 4 m/d時，庫岸邊坡穩定系數最小。這主要是由于滲透系數小于庫水水位下降的速率v時，坡體內水壓力產生滯后反應，坡體內部水壓力上升，基質吸力增加幅度較小，因而邊坡穩定系數也明顯降低。對于組合1、6、8，該組合下滲透系數k大于庫水水位下降的速率v，該庫岸邊坡坡體穩定系數明顯較其它組合下的庫岸邊坡穩定系數大。

5 結 論

本文以平頂水庫作為研究對象，對該水庫庫岸邊坡建立FLAC數值分析模型，分析了相流對邊坡穩定性計算結果的影響、不同工況下的孔隙水壓力變化以及采用正交試驗對影響邊坡穩定的因素進行分析。主要結論如下：

1) 基質吸力是影響岸坡穩定性的關鍵因素，采用兩相流的分析方法，基質吸力作用與實際更加符合。

2) 在合理的庫水水位下降速率調配下，對滲流作用的土體孔隙水壓力影響不大，滲透系數對孔隙水壓力的影響較大，邊坡坡度越大越有利于坡體內應力的消散。

3) 庫岸邊坡穩定系數隨著水位高度下降呈現先減小后增大的變化趨勢，最小值位于H=20 m左右。隨著庫水水位下降的速率v增大，水位下降高度相同時，庫岸邊坡穩定性最差；庫岸邊坡坡度β是庫岸邊坡坡體初始應力狀態的關鍵影響因素；滲透系數k與水位下降速率v的相對值是邊坡穩定系數的重要影響因素。