面向火箭子級精確回收的翼傘最優航跡規劃算法研究

邢小軍, 韓逸塵, 樊國政, 陳夢萍, 李豐浩

(西北工業大學 自動化學院, 陜西 西安 710072)

當前,運載火箭子級的無損精確回收及可重復使用已經成為國際航天領域的研究熱點。運載火箭子級回收的方式主要分為帶翼飛回、垂直反推以及傘降回收3種。其中傘降回收方式主要有降落傘回收和翼傘回收2種[1]。相比于降落傘,翼傘具有出色的滑翔性以及可操縱性,是實現火箭子級回收的重要手段。這其中如何規劃合理的翼傘回收航跡以實現子級的落點準確對保障地面人員的生命、財產安全及航天器的安全回收尤為重要。

基于翼傘進行火箭一子級回收主要采用徑向歸航、錐形歸航和非比例控制等歸航方式[2-3],但這些歸航方式存在如下問題:①翼傘操縱比較頻繁,難以實現逆風著陸;②接近目標點時容易造成翼傘頻繁控制,消耗能量過多;③實現復雜,且歸航精度較低。當前,分段歸航策略成為翼傘航跡設計的主要方式[4]。國內外學者對分段歸航做了很多研究,如文獻[5-6]將最優控制與分段歸航相結合,并且進行了仿真驗證。文獻[7-8]研究了翼傘的最優控制歸航方案,在分段歸航的基礎上考慮了地形威脅和風場的影響,將航跡尋優問題轉換成參數尋優問題,應用粒子群算法實現了最優航跡規劃等。

但上述研究未考慮翼傘不同轉彎下偏量對火箭子級速度的影響,且未將分段歸航的盤旋削高圈數作為規劃目標,易導致翼傘控制機構能量過度消耗。此外,粒子群算法計算耗時、迭代緩慢會降低航跡規劃效率。為此,本文針對某固體運載火箭一子級翼傘回收,主要研究翼傘不同轉彎下偏量對一子級速度及航跡的影響,并提出一種基于天牛群算法的低能耗、高效率的翼傘一子級航跡規劃算法。

1 火箭一子級翼傘組合體建模

在翼傘航跡規劃中可將翼傘和火箭一子級組合體視為剛體,為更方便地分析翼傘運動對一子級及組合體姿態和航跡的影響,本節首先根據火箭一子級和翼傘的動力學和運動學方程建立組合體的六自由度模型,并分析翼傘在不同轉彎半徑下對組合體速度的影響。

1.1 假設條件

為簡化分析,對翼傘建模做如下理想化假設:

1) 翼傘完全打開充滿氣后,展開形狀為固定的對稱形(除去存在下拉量的情況);

2) 傘衣質心與壓心重合,位置在弦上距前緣1/4。

1.2 運動學和動力學方程

表1列出了某型火箭一子級翼傘組合體的主要氣動系數,其他參數請參考文獻[9]中的具體數據。

表1 火箭一子級翼傘組合體氣動系數

翼傘一子級組合體運動學方程為

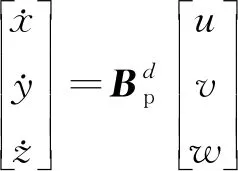
(1)

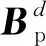
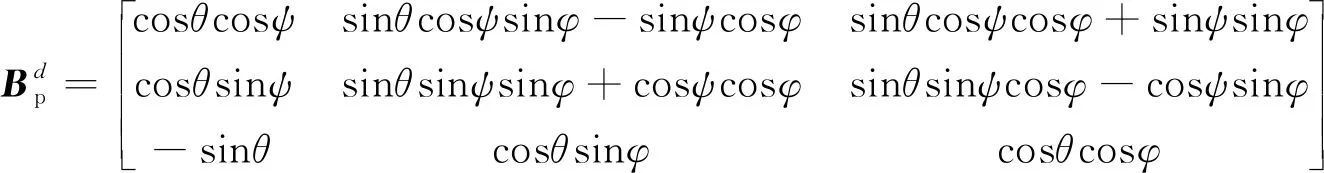
(2)

式中,φ,θ,ψ分別表示組合體的滾轉角、俯仰角和偏航角。

翼傘一子級組合體的動力學方程為

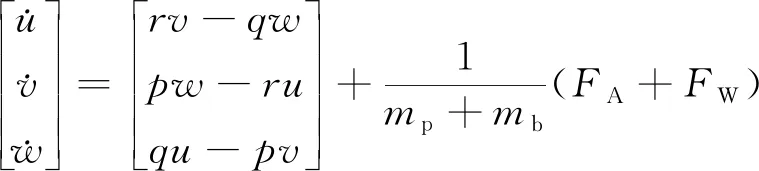
(3)

式中:FA為氣動力在組合體三軸上的分量;FW為重力在機體坐標系上的分量;[p,q,r]為機體坐標系中組合體的角速度;mp為翼傘的質量;mb為一子級的質量。

火箭一子級翼傘組合體的角運動方程為

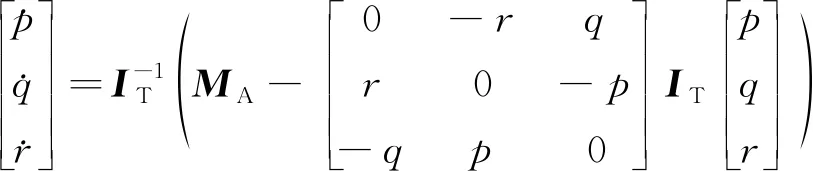
(4)

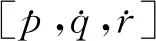
火箭一子級翼傘組合體的歐拉角變化率與機體坐標系的3個角速度分量之間的關系式可以寫為

(5)

2 基于天牛群算法分段最優航跡規劃

火箭一子級翼傘組合體的航跡反映了組合體質點的運動軌跡,航跡規劃采用分階段設計方式,可體現出火箭一子級翼傘組合體的位置及航向角變化。因此,本文首先通過火箭一子級翼傘組合體六自由度模型分析翼傘不同轉彎下偏量對組合體速度及航跡的影響,并在航跡規劃中予以考慮。此外,為降低翼傘航跡規劃的復雜度,進一步將六自由度模型簡化為質點模型。

2.1 質點模型

在風場方向水平、大小已知的情況下,取大地坐標系,水平風向為x軸方向,按照右手準則確定y軸方向,z軸為垂直于地面向上,則火箭一子級翼傘組合體的模型可以簡化為

(6)

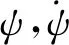
2.2 航跡分階段設計

基于分段歸航方案[10],航跡分為飛行段、盤旋削高段和雀降段[11],圖1為分段歸航航跡示意圖。

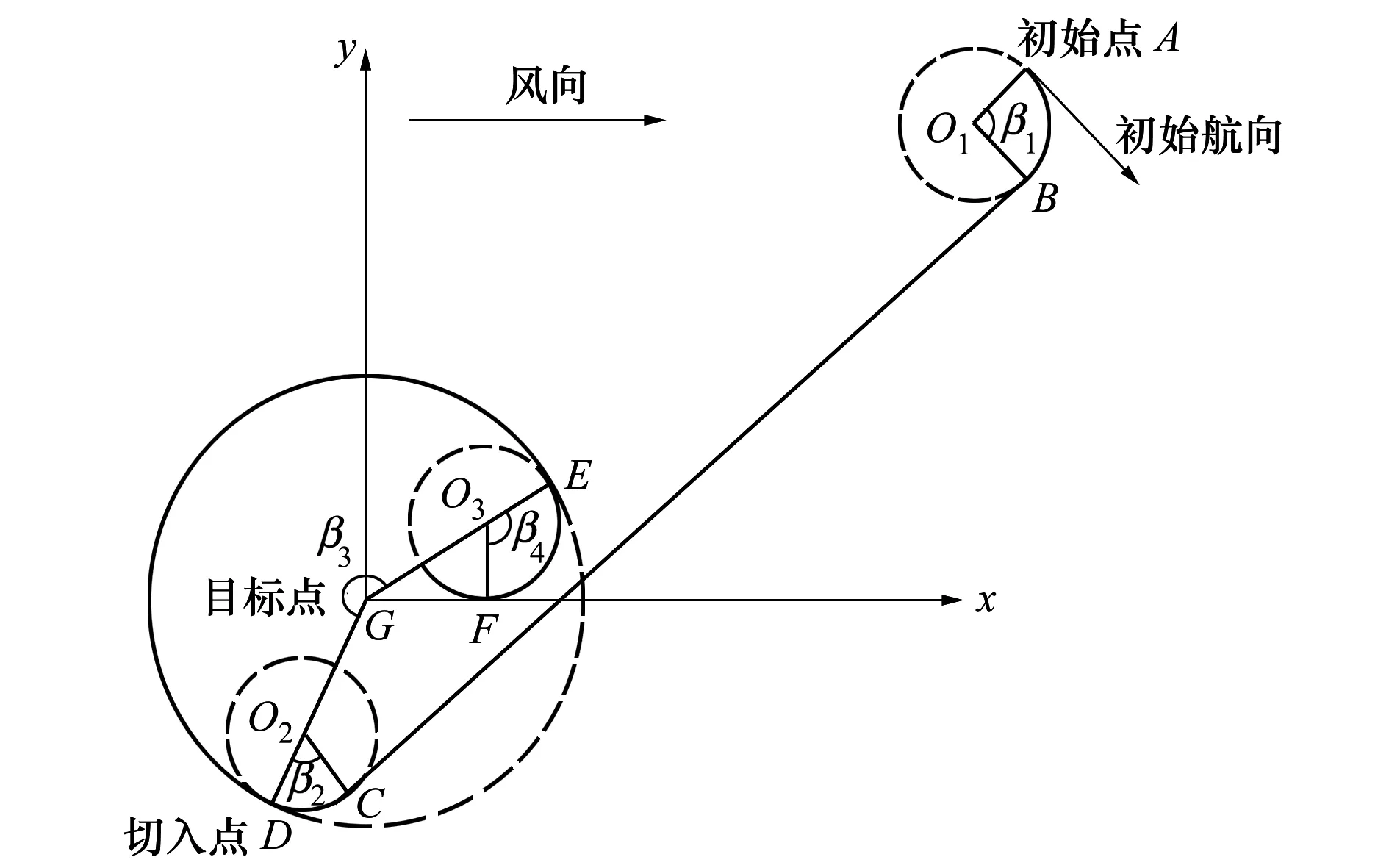
圖1 分段歸航航跡示意圖

其中BC段為飛行段,DE段為盤旋削高段,FG段為雀降段,AB、CD、EF段為圓弧過渡段,β1,β2分別表示圓弧過渡段弧度;β3表示盤旋階段的圓弧段弧度;β4為盤旋削高段和雀降段之間的過渡段弧度,是盤旋削高段末尾速度方向和逆風方向的夾角,可通過調整β4確保雀降段能夠逆風著陸。顯然,根據圖1可以很容易得出各段航跡的幾何關系。

本文翼傘航跡規劃的目標是確定盤旋削高段和雀降段切入點的最優坐標,以保證組合體在雀降段能夠逆風著陸于目標點,同時能量消耗盡可能低。由于不同的盤旋半徑對應不同的前向速度和垂直速度,盤旋階段的盤旋半徑表達式為

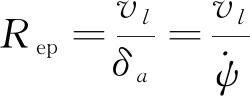
(7)

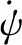
再以能量消耗最小以及落點偏差最小為優化目標,首先構造如(8)式所示的函數

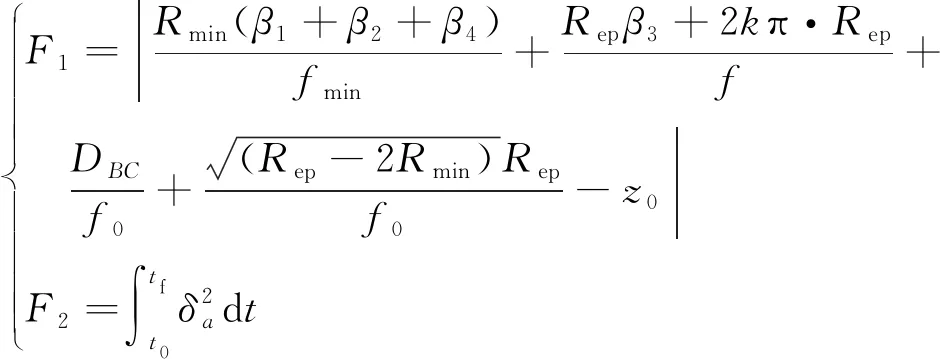
(8)

式中：f0為組合體穩定滑翔狀態下的滑翔比;fmin為組合體最小轉彎半徑時的滑翔比;f為組合體盤旋削高階段時的滑翔比;2kπ·Rep為盤旋階段過程中盤旋段整圓周的水平距離;z0為翼傘開始工作時一子級高度。F1為組合體著陸時的偏差,即設計的一子級航跡的垂直海拔高度與不同階段下各水平飛行距離通過滑翔比轉化成的高度總和之差的絕對值。DBC為BC段的直線長度。

取最終目標函數為

F=min{k1F1+k2F2}

(9)

本節中設定F1的權重系數為0.8,F2的權重系數為0.2。

2.3 天牛群算法

本文采用天牛群算法[12-13]對(9)式所示的目標函數進行優化。

設有N只天牛,分別表示為l=(l1,l2,…,lN),每只天牛的位置可以定義為li=(Repi,θepi,ki)T,也表示一個可能的函數最優解;將其帶入到設定的目標函數中,得出每個天牛位置的適應度值;完成該位置計算后,天牛的位置會發生變化,用vi=(vi1,vi2,vi3)T表示天牛位置變化時的速度,速度更新表達式為

(10)

式中:r1和r2為[0,1]之間均勻分布的隨機數；s=1,2,3;i=1,2,..N;pbesti=(pbesti1,pbesti2,pbesti3)T為當前個體的最優值,并且將所有個體的最優解中的最小值作為全局最優解gbest=(gbest1,gbest2,gbest3)T；n表示當前正在進行的迭代次數,學習因子c1,c2為常數,慣性權重系數ω隨過程變化,變化規律為

w=wmax-(wmax-wmin)·i/I

(11)

I為最大迭代次數，天牛位置的更新規律為

(12)

Ybi=st·r3·sign(fleft-fright)

(13)

式中，f(x)表示天牛位置的氣味濃度,也稱為適應度函數,其最大或最小值對應于氣味源點,代表所求目標函數。r3為[0,1]之間均勻分布的隨機數組成的1×3向量；根據天牛位置計算每個天牛的左側距離xleft和適應度fleft及右側距離xright和適應度fright

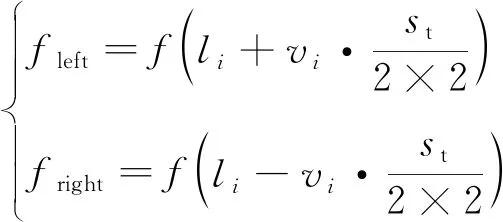
(14)

對天牛的步長以及2個觸角的質心之間的距離進行更新

(15)

(16)

(15)式中δ為步長的衰減系數,d0為天牛兩須之間的距離,e為自然常數。

基于天牛群算法對上述3個未知參數Rep,θep,k尋優的具體流程如圖2所示。

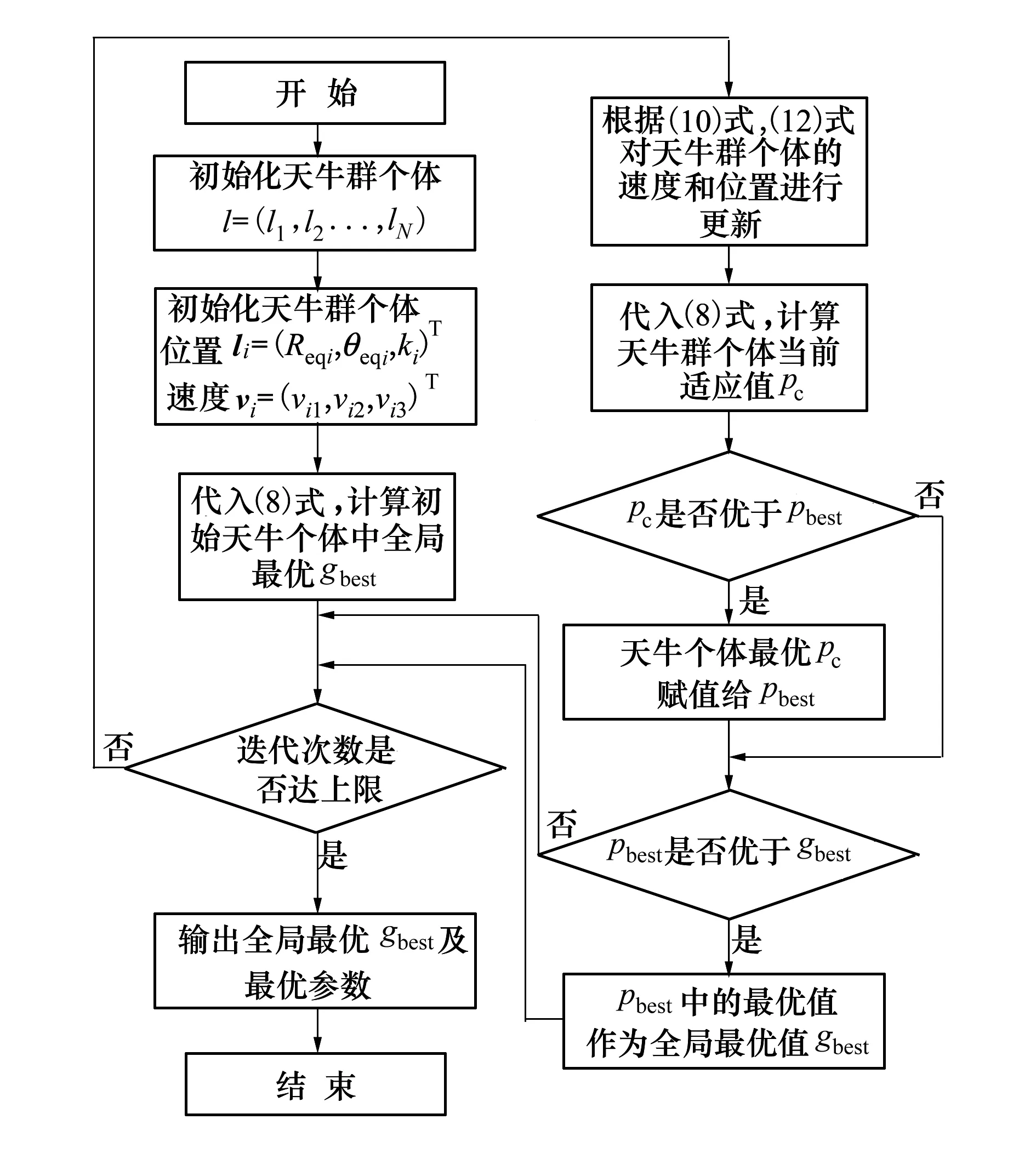
圖2 天牛群算法流程圖

將尋優的結果代入到分段歸航航跡中,得出每段航跡起始點坐標,計算出每個分段航跡的期望控制輸入量(偏航角速率)、作用時間,再結合(6)式得出歸航航跡。

3 仿真實驗

3.1 翼傘一子級組合體下偏量仿真結果

已知翼傘一子級組合體轉動慣量矩陣為

組合體總質量mp+mb為1 900 kg。假設組合體初始位置為(0,0,7 000)m,初始速度為(10,0,40)m/s,初始歐拉角為(-60°,0°,0°),初始歐拉角速度為(0,0,0)(°)/s,計算翼傘不同轉彎下偏量的組合體前向速度和垂直速度,并對前向速度、垂直速度與轉彎下偏量進行擬合,得出前向速度與轉彎下偏量之間的數學關系式為

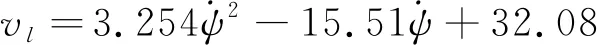
(17)

垂直速度與轉彎下偏量之間的數學關系式為

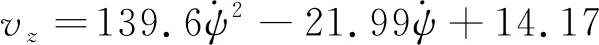
(18)

3.2 最優航跡規劃仿真結果

圖3 天牛群算法和粒子群算法收斂曲線

圖3給出了天牛群算法和粒子群算法的收斂性以及函數尋優結果。可以看出,天牛群算法的收斂速度更快。此外通過多次算法尋優可知,天牛群算法的最優值收斂于16.725左右,而粒子群算法尋得的最優值在20.899左右。由此可見,相對于粒子群算法,天牛群算法由于在尋優過程中加入了天牛粒子自身的判斷,從而降低了陷入局部最優的概率,同時收斂速度更快,尋優結果更好。

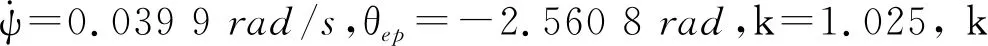
由圖4a)可得,最終航跡規劃的落點為(-489 9,-401 7,0.316 1)m,距離目標落點偏差為102.42m。從期望轉彎下偏量的變化曲線中可以看出,組合體的盤旋削高段期望轉彎下偏量為-0.039 9,轉彎半徑為788.63m。根據控制量曲線可以算出歸航的總能量消耗為1.587 5。

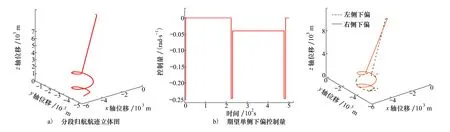
圖4 右側下偏規劃航跡 圖5 不同下偏方式規劃航跡

左側下偏與右側下偏的航跡結果如圖5所示。

由圖5可知,無論是左側下偏的逆時針轉彎運動還是右側下偏的順時針轉彎運動,規劃的航跡都能準確到達目標點。

對不同轉彎方法的落點偏差以及能量消耗統計結果如表2所示。可以看出,兩者規劃落點偏差僅10m,但能量消耗相差較大,這是因為目標點在初始飛行方向的右側,左側轉彎時需要以最小轉彎半徑左轉更大的角度,期望單側轉彎控制量作用時間長,所以理論上應根據初始飛行方向和目標點決定采用的轉彎方式,目標點在初始飛行方向左側時選擇左側轉彎,在右側時選擇右側轉彎。

表2 左右下偏歸航指標對比(擬合后)

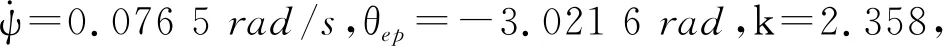
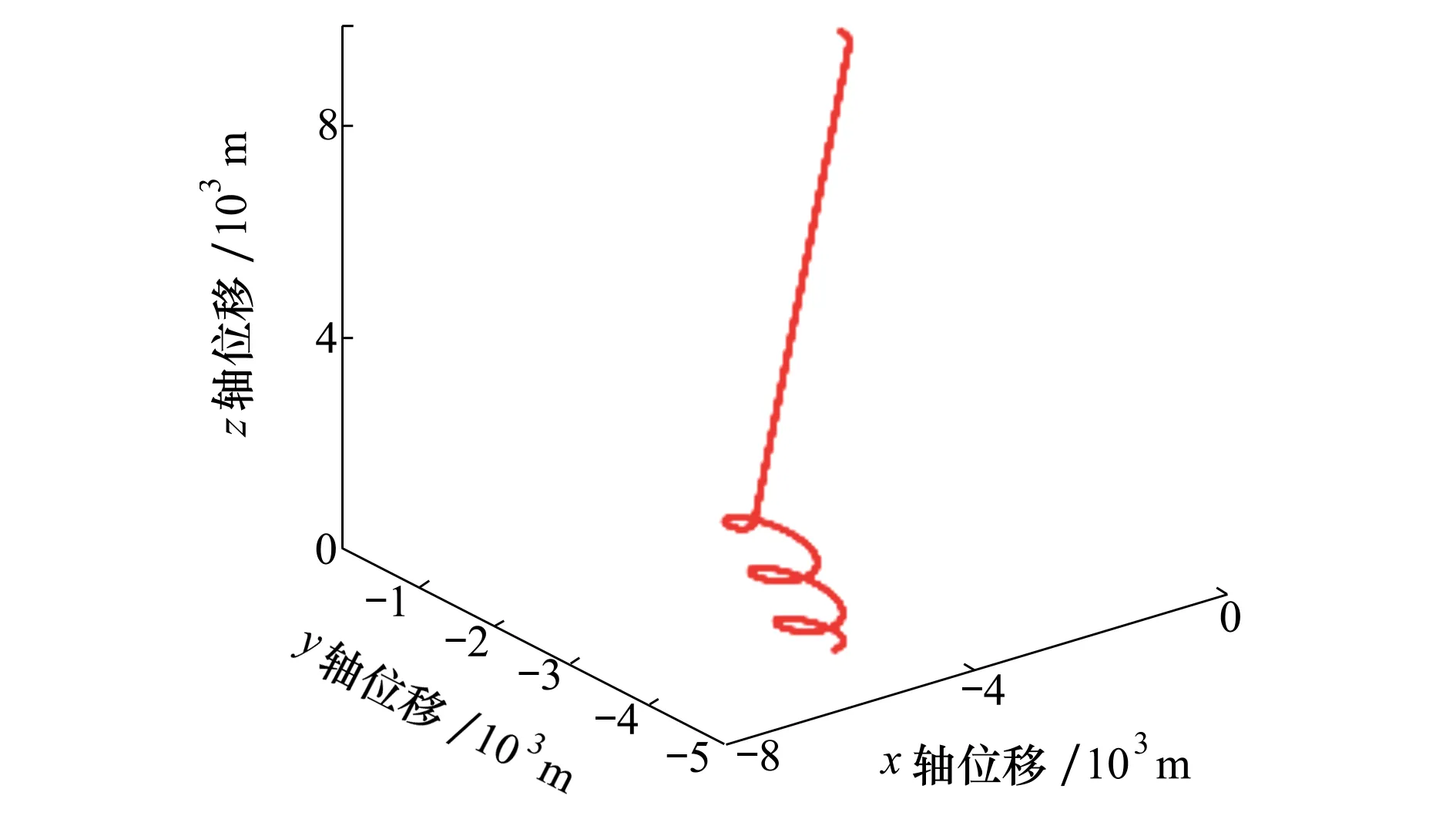
圖6 常值風下的分段歸航航跡

由圖6可知,最終規劃落點坐標為(-4 992,4 003,-1.404)m,速度為(-24.47,0,10.7)m/s火箭一子級翼傘組合體的雀降段方向為x軸負向,為逆風雀降,滿足要求。

4 結 論

本文通過翼傘和火箭一子級組合體的六自由度模型仿真得到翼傘轉彎下偏量對前向速度、垂直速度的影響并擬合出數學關系加入到航跡規劃的過程中,可以使各航跡段更貼近于高保真模型的飛行速度,減少后續的航跡跟蹤控制的難度;采用天牛須算法進行航跡規劃的參數尋優,相較于粒子群算法尋優速度更快,并且優化了粒子群算法容易陷入局部最優的缺點;在考慮能量最優的同時,將盤旋削高的圈數作為尋優目標之一,仿真結果表明該航跡規劃算法能夠在風場影響下規劃出落點精準的火箭一子級回收航跡。