一次提升“四能”的探究之旅
——從一道三角不等式的教學談起*
2022-04-21 14:20:28李勤儉安徽省池州市第一中學247000
中學數學雜志 2022年4期
李勤儉 (安徽省池州市第一中學 247000)
在高中數學教學中，教師有意識地引導學生進行思考，從數學角度發現和提出問題、分析和解決問題，不僅是新課程標準的要求，也能高效地提高學生自主學習的能力．本文從一個正弦定理推證過程中得到的三角不等式入手，探討如何在解題教學中提升學生的“四能”．
1 發現問題，提出問題
在三角形中，有正弦定理其中在證明“=2R
”的過程中，文[1]得到了如下的三角不等式①．那么不等式①如何證明呢？2 分析問題，問題解決
不等式①的左邊看起來比較正常，但右邊就讓人難以接受．看到π，聯想到幾何意義，所以從圓入手也算自然；①式是代數式，理應有代數證法，那么作為三角函數式，可以從三角變換角度去解決；同時，從式子的結構出發，可以看成是余弦函數相關問題，所以從函數角度分析應該也能解決問題．
2.1 幾何證法
在圖1中，圓O
是△ABC
的外接圓.
下面分△ABC
是銳角三角形、直角三角形和鈍角三角形三種情形證明.
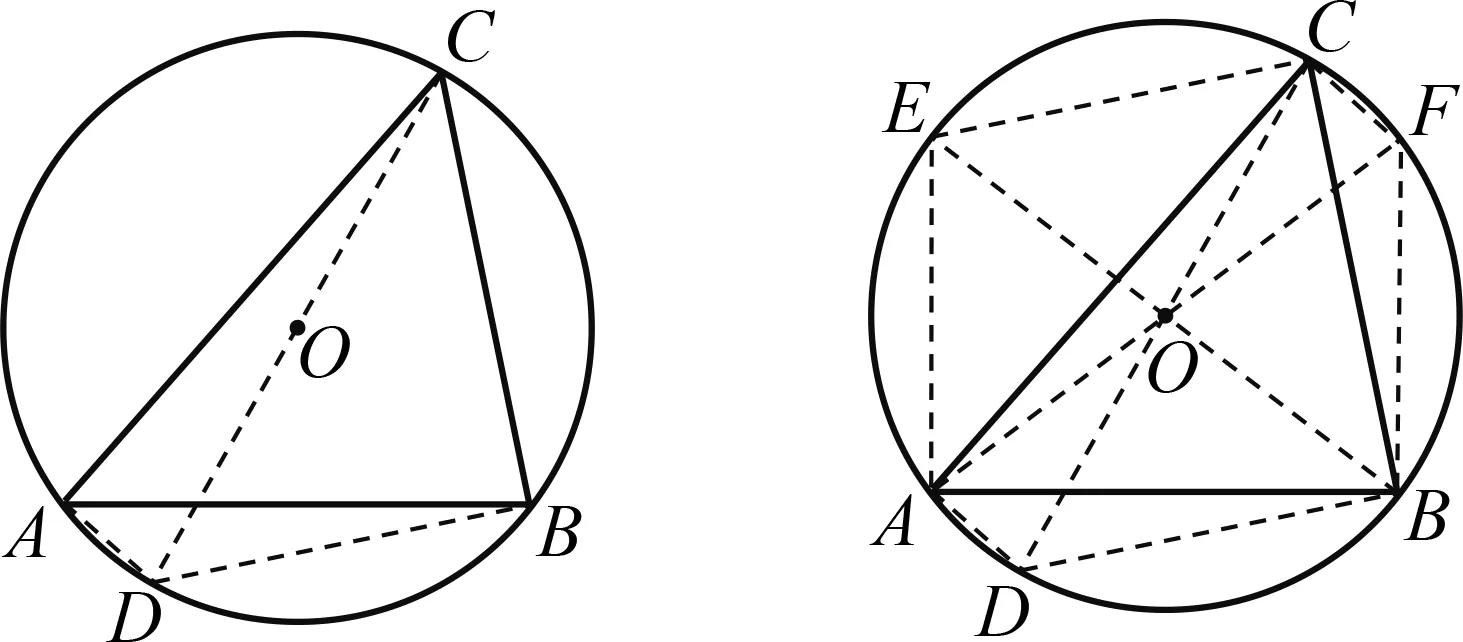
圖1 圖2
證明
(1)當△ABC
是銳角三角形時，如 圖2，連結BO
，AO
并延長分別交圓O
于點E
，F
，再連結BF
,FC
,CE
,EA
，則BF
=2R
cosC
,FC
=2R
cosB
,BD
=2R
cosA.
在四邊形CDBF
中，顯然有CD
<DB
+BF
+FC
<半圓弧，即2R
<2R
cosA
+ 2R
cosB
+2R
cosC
<πR
，故1B
+cos(2)當△ABC
是直角三角形時，不妨設C
=90°，此時C
=0，從而cosA
+ cosB
+cosC
=sinA
+cos即1B
+cos(3)當△ABC
是鈍角三角形時，不妨設C
>90°，此時可將圖2中的點D
與點C
對換，轉化為情形(1)，得證.
幾何證法直觀、好理解，但不容易想到.
我們再嘗試用代數證法．2.2 代數證法
先證cosA
+cosB
+cosC
>1 ②．因為cosA
+cosB
+cosC
即+1 ③.
又A
,B
,C
∈(0,π),故均大于0，因此cosA
+cosB
+cosC
>1.
再證④．
為了證④式，先證下式：
=1 ⑤.
=1.
另一方面，在⑤式中，有如下變形:
令則上式即為2t
+3t
-1≤0?(t
+1)(2t
-1)≤0． 因為t
>0,所以從而將此式代入③式，得即④式得證.
由②④可得①式得證.
由此還可以順帶得①式的加強式：
⑥.
2.3 琴生不等式證法
下面用琴生不等式證明
琴生不等式(Jensen Inequality)：
函數f
(x
)是定義在開區間(a
,b
)上的凸函數.
設λ
,λ
，…，λ
是n
個正實數，且λ
+λ
+…+λ
=1，x
,x
,…,x
是開區間(a
,b
)上任意n
個點，則下面不等式成立：f
(λ
x
+λ
x
+…+λ
x
)≥λ
f
(x
)+λ
f
(x
)+…+λ
f
(x
).
這個不等式稱為琴生不等式.
(注意:對于凹函數(下凸函數)，上式中的“≥”變為“≤”)當△ABC
是銳角或直角三角形時，函數f
(x
)=cosx
在上是凸函數，則即故1B
+cos當△ABC
是鈍角三角形時，不妨設C
>90°，則利用琴生不等式得即cosA
+cos故cosA
+cosB
+cosC
≤3 再次提出問題
一個問題從提出到解決，并不是思維過程的結束，而往往是新問題的開始.
①式是針對余弦函數而言的，那么對于正弦函數、正切函數，相應的結論是什么？又如何證明？3.1 與正弦函數有關的不等式
經過探討分析得到
⑦．
分析 一方面，不等式sinA
+sinB
+ sinC
>0顯然成立；另一方面，由于正弦函數在(0，π)上是凸函數，所以由琴生不等式容易得到sinA
+sinB
+sin從而⑦式成立.
(注：其他證法請讀者自行思考)3.2 與正切函數有關的不等式
當△ABC
是銳角三角形時，⑧．
分析 顯然△ABC
是直角三角形時，正切沒有意義；由于A
=B
=30°,C
=120°時，所以當△ABC
是鈍角三角形時，亦不成立.
證法1
(琴生不等式)當△ABC
是銳角三角形時，f
(x
)=tanx
在上是凹函數，所以有tanA
+tanB
+tan證法2
(琴生不等式+
函數法)由琴生不等式，易得tanA
+tan故tanA
+tanB
+tan設則上式右邊
令f
(t
)=t
(1-t
)，則f
′(t
)=-3t
+1,故從而綜上所述，
證法3
(基本不等式法)因為在△ABC
中，有tanA
+tanB
+tanC
=tanA
·tanB
·tanC
，當△ABC
為銳角三角形時，tanA
>0,tanB
>0,tanC
>0，所以由基本不等式得tanA
+tanB
+tanC
=tanA
·tanB
·tan,從而tanA
·tanB
·tan即tanA
+ tanB
+tan4 幾點感悟
在學習數學的過程中，發現問題往往比證明結論更重要.《普通高中數學課程標準(2017年版)》提出了“四能”，因此教師需要適時、適度地引導學生發現、提出一些數學問題，進而分析和解決問題，促進學生數學水平的提高.
(1)引導學生學會提出問題的方法應成為教學中的一個重要內容.本文由余弦函數的一個優美的不等關系，運用合情推理的方法拓展到了與正弦和正切函數相關的性質.如何引導學生學會提出問題，也許比幫助學生解決問題更有意義.
(2)對一個問題的解決進行多角度思考是數學探究的基本思路.文中對不等式①的證法進行了多角度的思考，得到了很好的思維體驗.這意味著教師在教學過程中如何進行多角度的思考，以及如何引導學生多角度思考是值得探索的一個課題．
(3)要在解決問題的過程中進行邏輯推理等核心素養的培養.本文在探討的過程中，包含了很多較深刻的分析與推理，使得學生在過程中學習，在過程中提高.
(4)探究無止境.文中通過探究得到了八個關系式，它們的應用又可作為新的探討課題.
在這一探討的旅程中，學生得到了很好的思維能力的訓練，以及分析問題和解決問題的能力訓練，體會到數學的嚴謹美、和諧美，提高了學習數學的興趣.這不正是新課程理念所要求的嗎？
猜你喜歡
小學生學習指導(中年級)(2022年4期)2022-04-26 06:34:46
今日農業(2021年9期)2021-11-26 07:41:24
中學生數理化·七年級數學人教版(2021年10期)2021-11-22 07:53:00
作文世界(小學版)(2018年4期)2018-10-16 17:13:34
數學小靈通·3-4年級(2017年10期)2017-11-08 08:42:51
快樂作文·低年級(2016年12期)2017-01-03 20:52:44
快樂作文·低年級(2016年6期)2016-06-24 18:58:40
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21
