聯合灰色模型和神經網絡的短期電力負荷預測

林懷德， 張剛， 郭啟波， 羅毅初

(廣東電網有限責任公司佛山供電局，廣東，佛山 528000)

0 引言

隨著我國經濟的快速發展和人民生活水平的日益提升，社會對電力能源的需求也呈現出指數級增長，在電力資源總量有限的前提下，為了盡可能地滿足用電需求，需要制定合理的電力生產計劃，以盡量避免電力資源浪費，在這種背景下，短期電力負荷預測就顯得尤為重要[1]。

目前國內外學者對短期電力負荷預測的研究主要可以分為統計類方法和機器學習類方法2種。統計類方法以多元線性回歸分析、指數平滑和時間序列等方法為代表，具有理論完備、計算簡單、線性預測精度高等優點，但是當面對復雜非線性問題時，該類方法的預測性能會出現明顯下降[2-3]。機器學習類方法是近年來隨著人工智能技術的興起而得到快速發展的一類新方法，以支持向量機(Support Vector Machine, SVM)和人工神經網絡為代表，其中SVM在面對小樣本、非線性擬合問題時具有獨特優勢，但是存在過擬合，且對核函數、模型參數較為敏感的問題[4]，人工神經網絡具有強大的多元映射能力，特別適合于對非線性系統的預測，被廣泛應用于短期電力負荷預測中，但是人工神經網絡算法普遍存在收斂速度慢、易陷入局部極小值問題[5]。

隨著電力數據規模越來越大，上述單一預測模型結構越來越復雜、參數調整越來越困難，若要進一步提升預測性能，采用集成多種方法的組合模型勢在必行。本文提出一種聯合灰色模型(Grey Model, GM)和BP神經網絡的組合模型，該組合模型充分結合GM在小樣本、貧信息條件下的強預測能力和BP神經網絡任意非線性函數逼近能力，能夠實現對短期電力負荷的高精度預測，提升泛化能力，同時針對BP神經網絡初值選取困難，易陷入局部極小值的問題，提出一種改進粒子群優化算法(Improved Particle Swarm Optimization, ImPSO)自動進行全局尋優，確保模型收斂于全局最優解。

1 灰色-BP神經網絡組合模型

1.1 灰色預測模型

電網系統運維過程中，影響電力負荷的因素復雜多樣，例如溫度、濕度、季節、經濟形勢、人員活動等，這些因素中有些是明確可知的，有些則是難以定量衡量的，屬于灰色理論范疇，因此可以采用灰色理論進行預測。目測常用的灰色預測模型為GM(1,1)[6]。

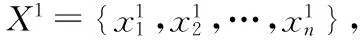
(1)

通過累加運算可以將數據中隱含的規律性信息顯示出來，從而增加數據的穩定性。

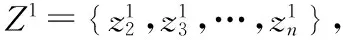
(2)

步驟3：根據如下式(3)構建GM(1,1)灰微分方程，

(3)

其中，a為發展系數，b為灰色作用量。式(3)對應的矩陣形式為

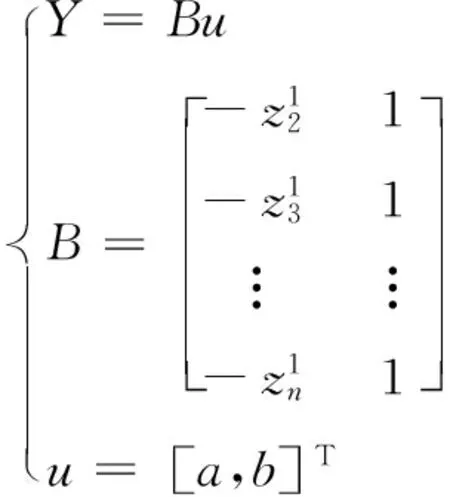
(4)

步驟4：利用最小二乘法對式(4)進行求解可得

(5)

步驟5：將式(5)計算得到的a和b值代入式(3)，可以得到GM(1,1)預測模型的表達式為

(6)

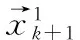
步驟6：對預測數據按式(7)進行一次累減運算，可以得到原數據的預測序列為

(7)

從上述算法步驟可知，GM(1,1)以差分方程為基礎，因此更適合于線性、平穩系統的數據分析和趨勢預測，當數據呈現出復雜非線性規律時，該模型的有效性會出現明顯下降，性能較差。

1.2 ImPSO-BP神經網絡

(1)BP神經網絡

圖1給出了BP神經網絡典型的3層拓撲架構，包括輸入層、隱含層和輸出層。作為一種前向反饋網絡，BP神經網絡的實現過程包括輸入層到輸出層的正向傳播過程和輸出層誤差到輸入層的反向傳播過程，通過正向傳播和反向傳播的循環迭代，網絡權值得到優化調整，從而使網絡實際輸出與預期輸出之間的誤差達到最小[7]。

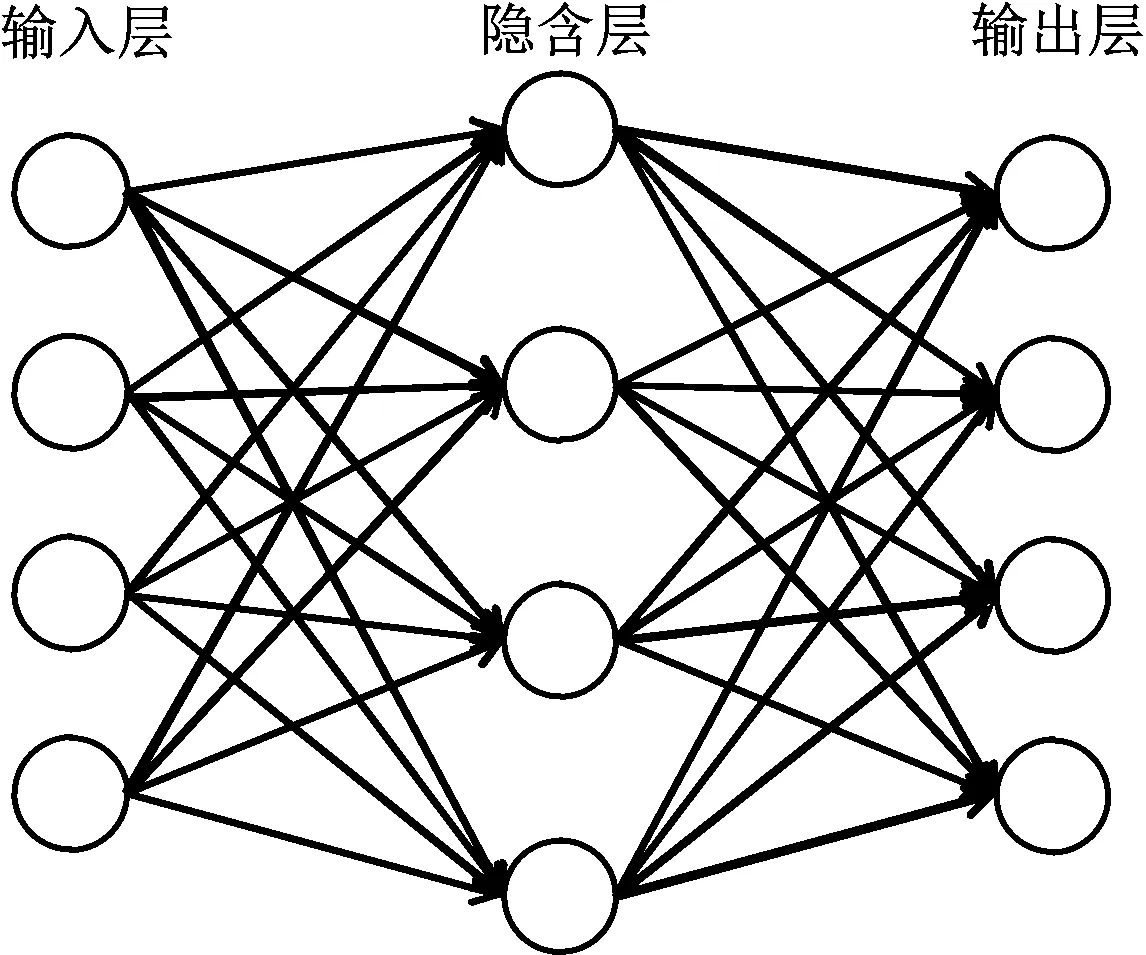
圖1 BP神經網絡典型3層拓撲架構

對于給定輸入層數據x1,…,xm，BP神經網絡的正向播過程包括輸入層映射到隱含層，隱含層映射到輸出層2步，式(8)給出了輸入層到隱含層的映射關系：

(8)

其中uj,j=1,…,N為隱含層神經元，w1,…,wn為權值，θj為閾值。

隱含層到輸出層的映射關系可以表示為

(9)

其中，yp,p=1,…,P為輸出神經元，f(·)通常采用Sigmoid型激活函數，ωpj為隱含層到輸出層的權值。

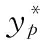
(10)

對式(10)采用梯度下降法，按照δ減小的方向依次由輸出層向輸入層方向調整權值和閾值，完成反向傳播過程。通過正向傳播的參數選擇和反向傳播的參數調整，BP神經網絡的實際輸出逐漸逼近于預期輸出，從而完成網絡自學習。

(2)ImPSO算法

由于BP神經網絡采用梯度下降法進行網絡學習，因此存在初值敏感的問題，初值選取不當會導致算法收斂于局部極值點，模型預測性能下降。粒子群優化(Particle Swarm Optimization, PSO)[8-9]算法作為一種在函數優化領域應用廣泛的隨機搜索方法，其基本思想是將鳥群中的每只鳥量化為一個只有速度和位置信息的粒子，每個粒子在搜索空間中將搜索到的最優位置作為個體極值，并將其與種群中的其他粒子共享從而確定整個群體中最優粒子當前的位置和速度，每個粒子通過對最優個體進行跟蹤來實現對自身位置和速度的更新，即：

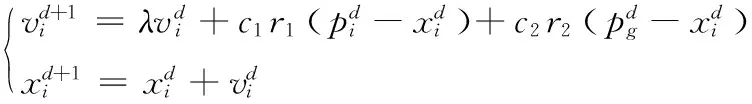
(11)

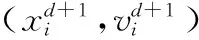
從式(11)可以看出，搜索步長λ決定著PSO算法的收斂性能。當λ取值較大時，模型的全局搜索能力提升，局部搜索能力下降，反之當λ取值較小時，模型的局部搜索能力提升，全局搜索能力下降。傳統PSO算法將λ設置為固定值的方式難以獲得全局搜索和局部搜索能力的均衡，因此本文對PSO算法進行改進，所提ImPSO利用式(12)所示線性遞減搜索步長代替傳統PSO的固定步長：

(12)

其中，t為當前迭代次數，T為總迭代次數，λmax和λmin為λ取值空間中的最大值和最小值。從式(12)可以看出，ImPSO在迭代開始粒子距離全局最優值較遠時，λ取較大值以保證全局搜索能力，隨著迭代的進行，粒子趨近于全局最優，此時λ取值減小，以提升局部搜索能力，確保收斂于全局最優解。

(3)ImPSO優化BP神經網絡

(2) 初始時,勵磁電流能夠產生定位力矩,定位力矩的峰值點對應著磁力線經過磁路最長的轉子位置,平衡點對應著磁力線經過磁路最短的轉子位置,因此通過定位力矩能夠進一步準確地判斷轉子位置。

根據上述分析，利用ImPSO對BP神經網絡初值進行全局尋優，提升BP神經網絡性能。具體流程如圖2所示，主要可以分為以下5個步驟。

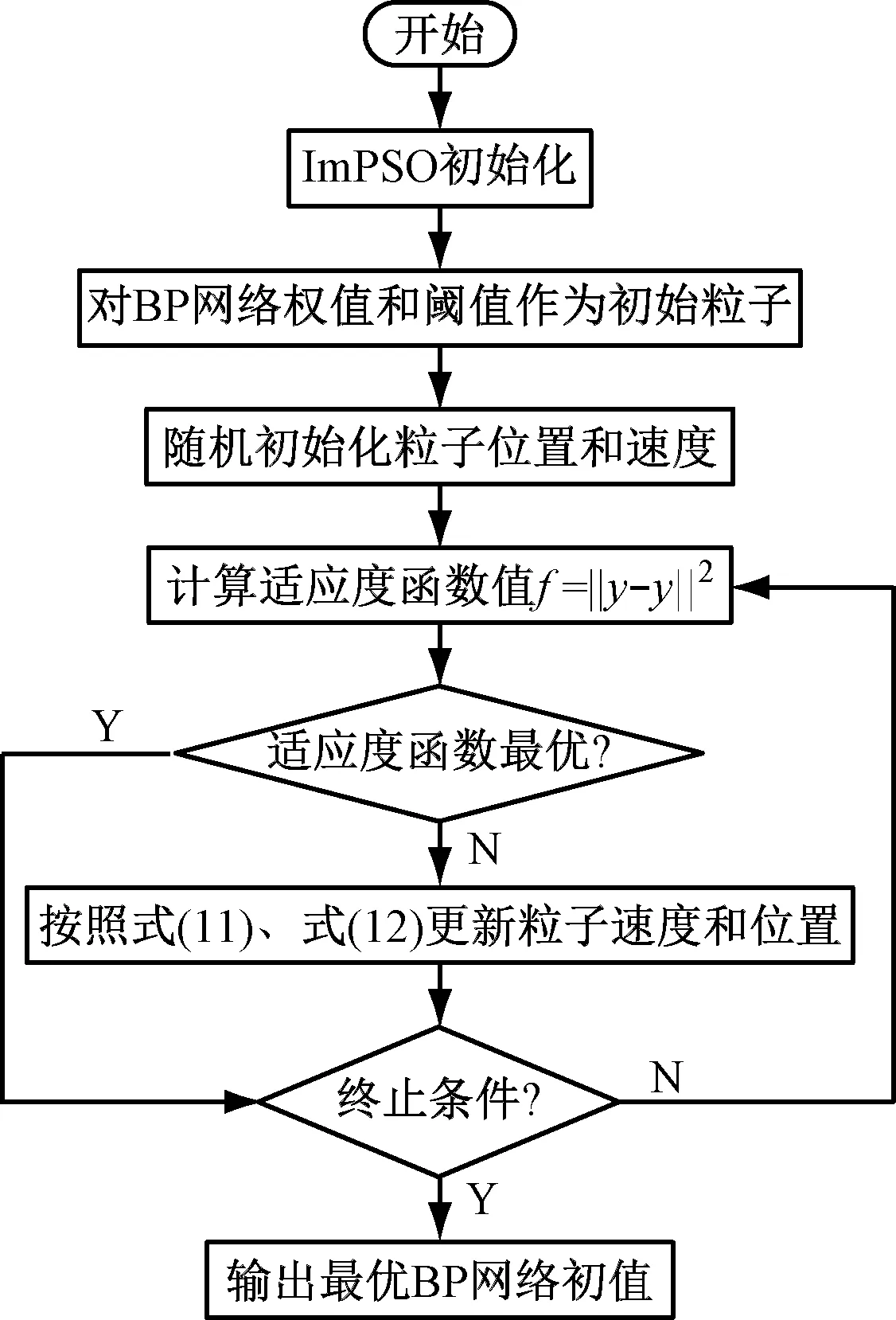
圖2 ImPSO優化BP神經網絡流程圖

步驟1：ImPSO初始化。設置種群數量，粒子位置和速度搜索空間，搜索步長取值區間以及算法最大迭代次數。

步驟2：對BP神經網絡模型初值賦予粒子。將BP神經網絡權值和閾值作為ImPSO算法的初始粒子，并在參數空間內隨機設置粒子的初始速度和位置。

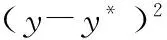
步驟4：根據式(11)和式(12)對粒子的位置和速度進行更新，并計算更新后的適應度函數值，若此時適應度函數值大于步驟3所得結果，則令更新后的粒子狀態為當前狀態。

步驟5：判斷是否滿足終止條件，若滿足則此時的粒子即為BP神經網絡的最優初值，否則轉至步驟3，繼續迭代。

1.3 組合預測模型

圖3 所提組合預測模型原理框圖

2 試驗結果及分析

2.1 不同樣本數量情況下的預測結果

為了驗證所提組合模型的短期電力負荷預測性能，采用廣東省某地區2018年3月11日至2018年5月11日共61 d的數據開展試驗。首先構建試驗驗證所提組合模型在不同訓練樣本數量情況下的預測性能，試驗中數據集的劃分形式如表1所示，即分別利用5月11日之前10 d—前60 d的數據作為訓練樣本完成模型訓練，對5月11日當天的電力負荷數據進行預測，得到的24 h平均預測結果如圖3所示，同時為了對比，圖3中一并給出了在相同條件下分別采用GM(1,1)模型和BP神經網絡模型得到的預測結果。可以看出，3種方法隨著訓練樣本數的增加，預測性能都出現了不同程度的提升，當訓練樣本數達到20 d時，所提組合模型的預測精度(95.7%)已經趨于平穩，接近于訓練樣本數為60 d的情形(96.9%)，而GM(1,1)模型預測性能接近最優時(60 d，91.5%)對應的訓練樣本數為30 d(90.8%)，BP神經網絡模型預測性能接近最優時(60 d，93.2%)所需的訓練樣本數為40 d(93.1%)，同時對于每種訓練樣本數量試驗，所提組合模型的預測性能均優于GM(1,1)模型和BP神經網絡模型。

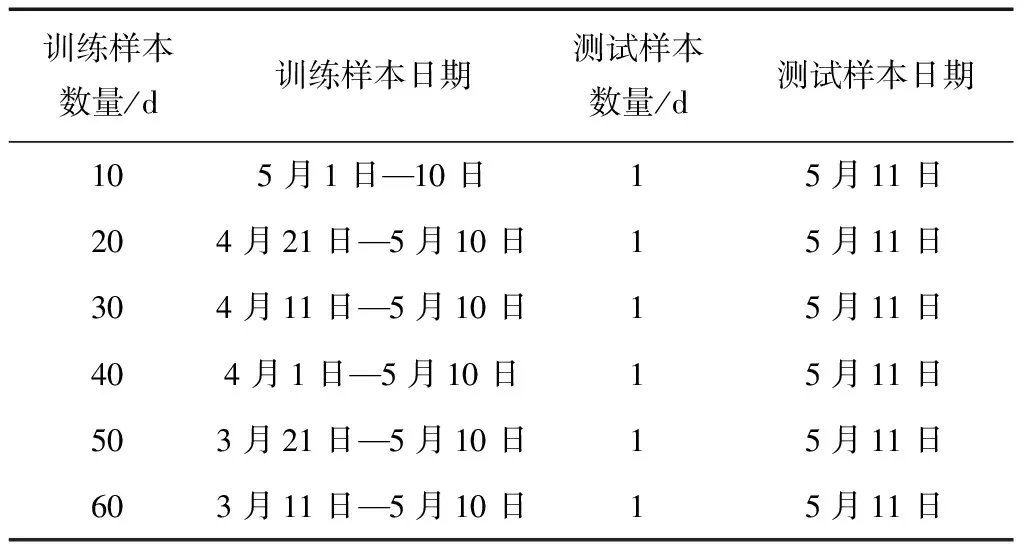
表1 不同樣本劃分方式

2.2 不同信噪比情況下的預測結果

實際工程實踐中，采集到的數據中不可避免地會存在隨機誤差和干擾等無用信息，為了進一步驗證不同方法在隨機誤差和干擾存在條件下的預測性能，采取向數據中加入高斯白噪聲的方式。同樣將2018年5月11日的數據作為測試數據，采用前60 d的數據作為訓練樣本，對訓練樣本中分別加入均值為0，噪聲方差為0.1～0.9的高斯白噪聲(噪聲方差的取值間隔為0.1)，采用3種方法開展預測試驗得到的結果如圖4所示，可以看出隨著噪聲方差的增大，3種方法的預測性能出現了不同程度的下降，其中，GM(1,1)模型性能下降最為明顯，BP神經網絡模型次之，而所提組合模型預測性能較為平穩，體現了更強的噪聲穩健性。同時從圖4可以看出，所提組合模型在不同信噪比條件下均能獲得最優的預測性能，在低信噪比條件下(噪聲方差大于0.4)，所提組合模型依然能夠獲得優于85%的預測準確度，而GM(1,1)模型和BP神經網絡模型的預測準確度已低于70%，不能滿足實際應用需求。

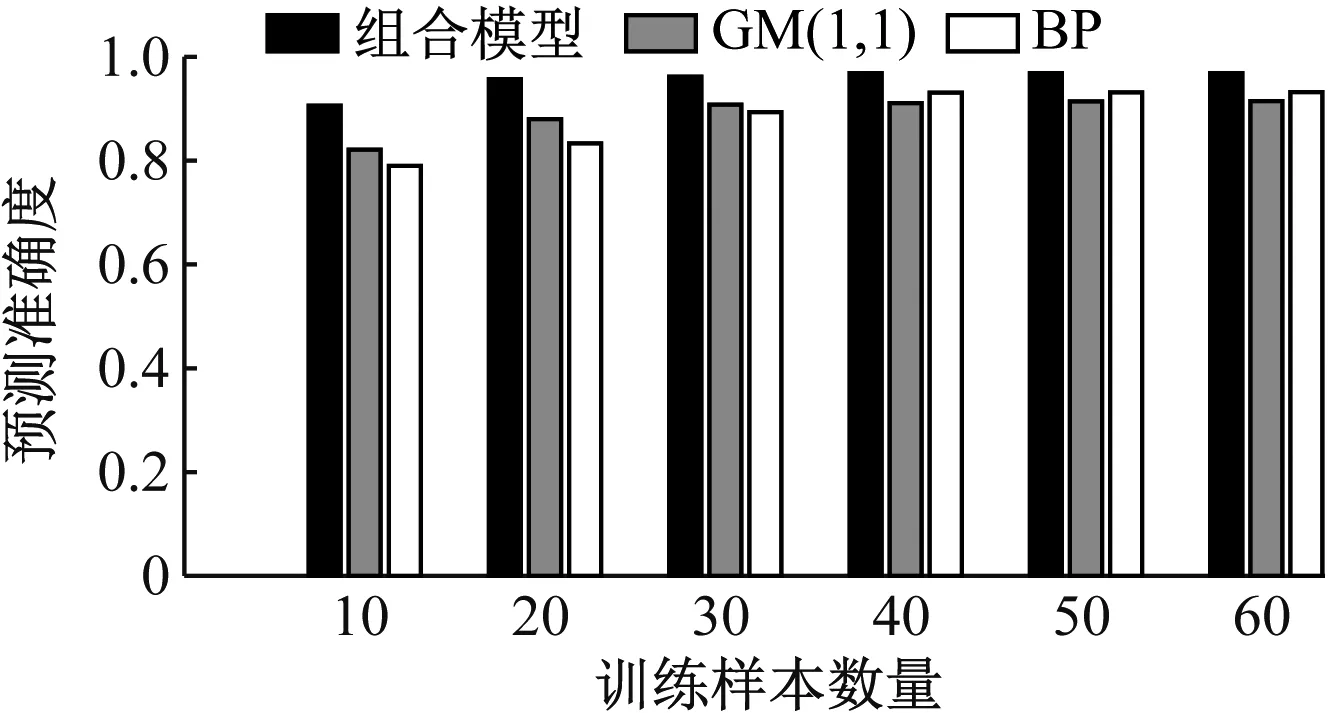
圖4 不同方法預測準確度

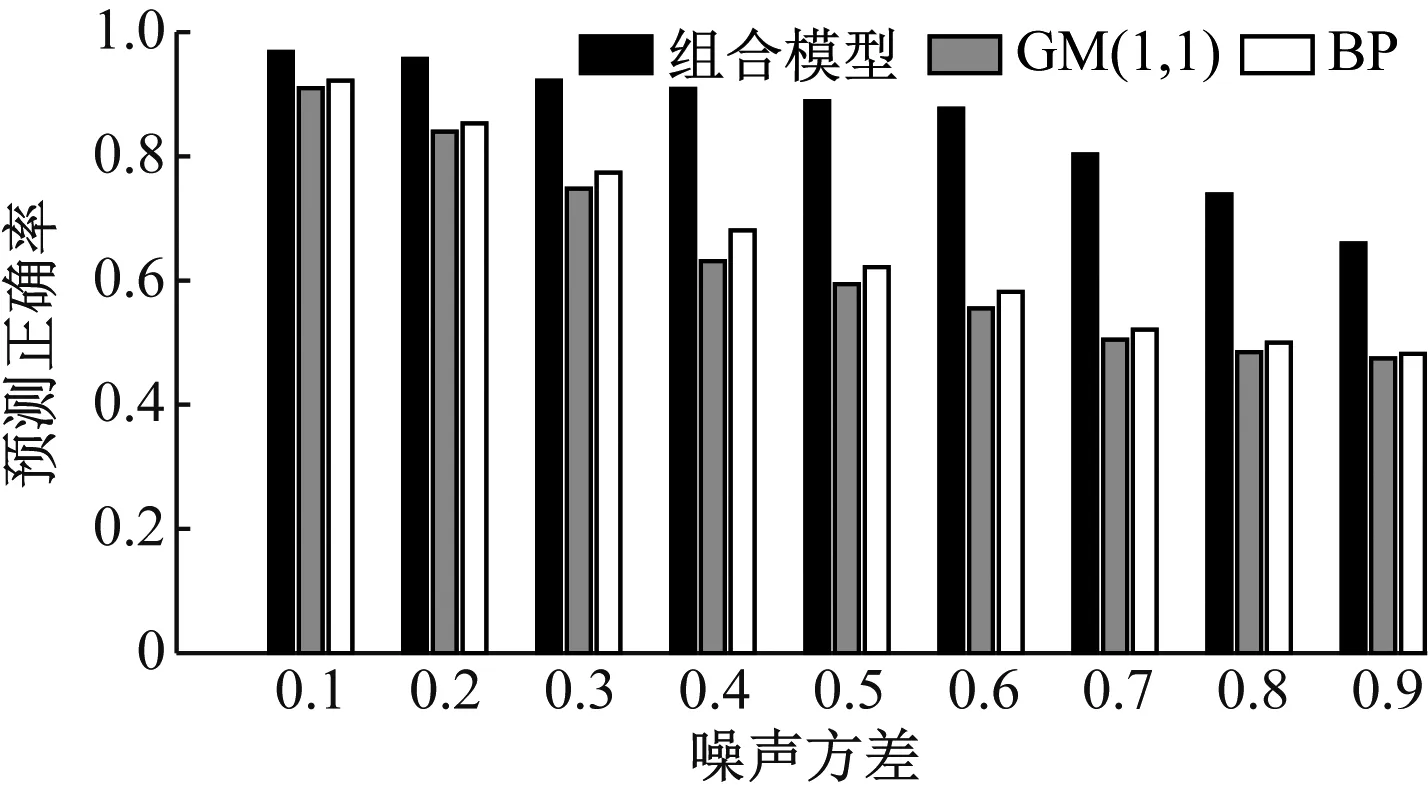
圖5 不同噪聲方差情況下的預測準確度

3 總結

隨著數字電力和智慧電網時代的到來，短期電力負荷預測精細化將是必然發展趨勢。針對多因素影響下單一模型預測精度低、泛化能力弱的問題，提出一種聯合GM(1,1)和ImPSO-BP神經網絡的組合預測模型，充分結合GM(1,1)模型在小樣本、貧信息條件下的預測能力和ImPSO-BP神經網絡的非線性逼近能力，基于廣東省某地區實際電力負荷數據的試驗結果表明，所提方法相對于單一GM(1,1)模型和BP神經網絡模型能夠獲得更高的預測精度，并且在小樣本、低信噪比條件下優勢更加明顯，具備較高的應用前景。