基于柱式傳感器表面光柵應(yīng)變分析

張 哲蓋廣洪李 煒

(航天動(dòng)力技術(shù)研究院，陜西 西安 710025)

布拉格光柵(FBG)由于其質(zhì)量輕、尺寸小、靈敏度高、抗電磁干擾等眾多優(yōu)勢(shì)[1]，引起了國(guó)內(nèi)外眾多學(xué)者研究。 光纖光柵傳感器可實(shí)現(xiàn)對(duì)應(yīng)變、溫度等物理參量實(shí)時(shí)監(jiān)測(cè)[2-3]，廣泛應(yīng)用于航天航空航海、橋梁隧道、智能儀器等領(lǐng)域，有著廣袤的前景。可由于基底對(duì)光纖的應(yīng)變傳遞效率受粘接材料、粘接工藝等多方面因素干擾，致使傳感器的精度受限。

對(duì)此類(lèi)問(wèn)題，國(guó)內(nèi)外學(xué)者研究開(kāi)展了眾多研究。ANSARIF 等人首次創(chuàng)建了基底傳遞應(yīng)變的數(shù)學(xué)模型，并且實(shí)驗(yàn)證明了其正確性[4]。 2006 年，LI Dongsheng 等人，假設(shè)光柵各層之間的應(yīng)變相等，進(jìn)而得出了更加準(zhǔn)確得應(yīng)變傳遞模型[5]。 2010 年前，粘接層材料還限于無(wú)機(jī)膠，有機(jī)膠材料才漸漸被用作粘接層，陳偉民等人將粘接層材料擴(kuò)充到金屬，為粘接層材料選擇擴(kuò)大了余地，吳俊[6]等人在此基礎(chǔ)上將粘接層替換為鉛，一定程度上提高了傳感器的精度。ZHOU J[7]使用有限元仿真軟件驗(yàn)證并對(duì)比了ANSARI F 和LI Dong-sheng 提出的埋入式FBG 傳感器應(yīng)變傳遞理論，理論上說(shuō)明了他們的精度可以更高，吳入軍[8]等人建立了埋入式方形粘接層的數(shù)學(xué)模型，用ANSYS 仿真軟件和實(shí)驗(yàn)論證了粘接層厚度和長(zhǎng)度對(duì)應(yīng)變傳遞效率的影響。 除此以外，光纖及涂覆層材料也是改變應(yīng)變傳遞效率的重要因素[9]。

但在被廣泛用作壓力傳感系統(tǒng)的柱式傳感器方面，應(yīng)變傳遞分析尚不成熟，傳感系統(tǒng)精度仍處于較低水平[10]。 本文在柱式傳感器表面建立力學(xué)傳遞模型，通過(guò)有限元仿真和實(shí)驗(yàn)驗(yàn)證了粘接層彈性模量以及厚度對(duì)柱式傳感器精度的影響，在實(shí)驗(yàn)工藝和粘接層參數(shù)上提高了傳感系統(tǒng)的精度，達(dá)到千分之五。

1 光柵傳感系統(tǒng)理論模型

1.1 光柵傳感機(jī)理

布拉格光柵(FBG)是一種能準(zhǔn)確感受應(yīng)變和溫度的光學(xué)傳感器，一般直接粘貼在傳感器表面來(lái)測(cè)量基底的應(yīng)變。 FBG 的傳感器機(jī)理為[11]:寬帶光在布拉格光柵中傳輸時(shí)，僅滿足中心波長(zhǎng)頻段條件的光會(huì)發(fā)生反射，其余均透射出去，且反射波長(zhǎng)的中心波長(zhǎng)變化量與應(yīng)變?yōu)榫€性關(guān)系。 如下所述:

式中:Mε＝1-Pε，Pε是有效彈光常數(shù)，為僅與光柵本身品質(zhì)相關(guān)的定值，λ為初始狀態(tài)的中心波長(zhǎng)。

1.2 基底與光柵應(yīng)變傳遞數(shù)學(xué)模型

布拉格光柵通過(guò)粘接劑固定在基底表面，以此來(lái)感受和傳遞基底的應(yīng)變，應(yīng)變測(cè)量通過(guò)解調(diào)儀和后端處理算法解算。 圖1 為柱式傳感器表面光柵的截面圖。

圖1 光柵截面圖

由于光纖直徑很小，在直徑為45 mm 的柱式傳感器表面，基底可以近似為直線。 粘接層為半徑為R的圓弧與基底、光纖相切，光纖與基底間距根據(jù)粘接層半徑R調(diào)整。 當(dāng)基底發(fā)生應(yīng)變時(shí)，由于基底、粘結(jié)層、光纖的彈性模量不同，粘結(jié)層和光纖會(huì)產(chǎn)生沿軸向的剪應(yīng)力，應(yīng)變是由基底向粘結(jié)層再向FBG傳遞，如圖2 所示。

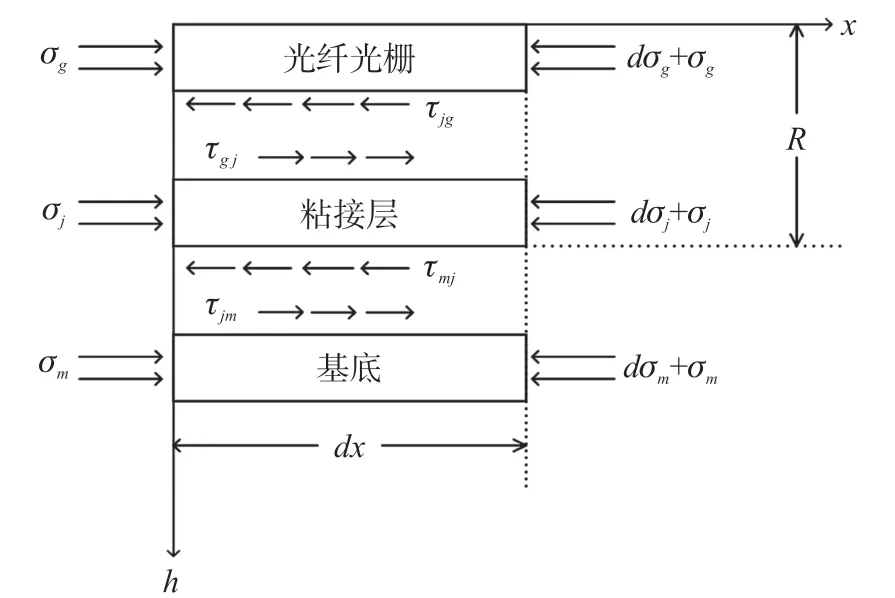
圖2 應(yīng)力傳遞示意圖

為了簡(jiǎn)化建模，本文做出以下假設(shè)[12]來(lái)建立基底表面應(yīng)變傳遞的數(shù)學(xué)模型:①基體、粘接層、光柵三者互相接觸位置沒(méi)有發(fā)生相對(duì)滑動(dòng)。 ②忽略形變過(guò)程中的溫度影響。 ③忽略泊松比帶來(lái)的影響。 ④假設(shè)光柵為統(tǒng)一整體，忽略纖芯、包層和涂覆層彈性模量不同的情況。

在柵區(qū)沿軸向取一段微元dx研究，首先對(duì)各層列出力平衡微分方程:

①FBG 微元段的平衡方程:

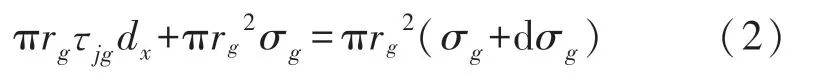
②粘接層微元段的平衡方程:

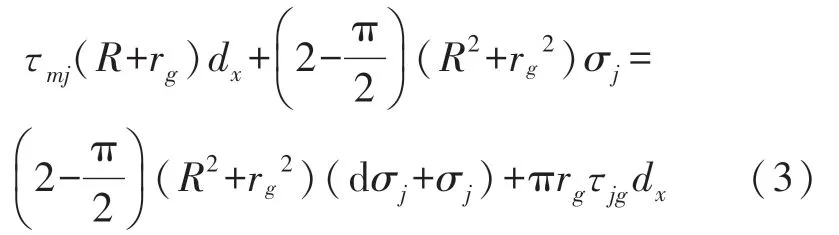
在忽略泊松效應(yīng)和其他方向上微小位移時(shí)，

根據(jù)應(yīng)力應(yīng)變基本公式[12]σ＝Eε，將式(4)代入后對(duì)式(2)、式(3)積分沿軸向積分得:

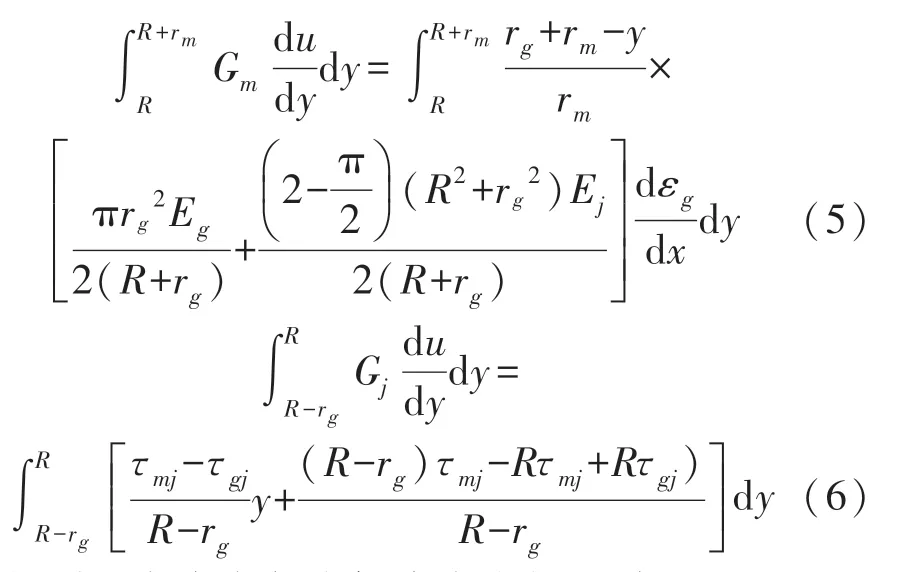
得到基底應(yīng)變與光柵應(yīng)變之間的關(guān)系:

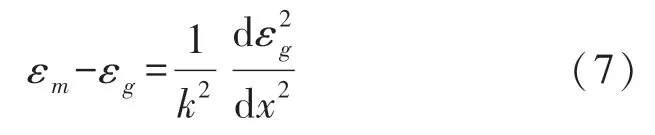
其中:

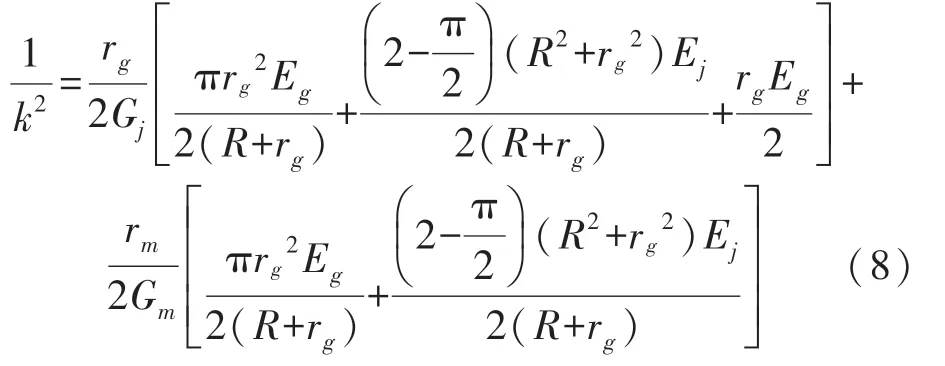
求解上述微分方程后得到應(yīng)變傳遞效率

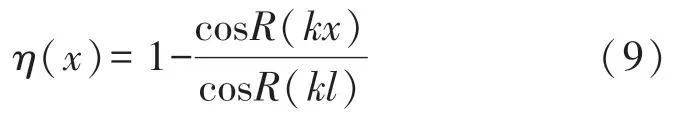
可見(jiàn)，應(yīng)變傳遞效率與粘接層厚度半徑R、粘接層長(zhǎng)度、粘接層彈性模量和光柵、基底等眾多參數(shù)有關(guān)，本文主要研究粘接層部分參數(shù)對(duì)柱式傳感器的精度影響。

表1 應(yīng)力應(yīng)變分析各參數(shù)說(shuō)明

2 FBG 有限元軟件仿真

為了驗(yàn)證上述理論模型的準(zhǔn)確性，并且為后續(xù)實(shí)驗(yàn)提供指導(dǎo)，本文使用商業(yè)CAE 軟件Ansys 進(jìn)行了有限元模型仿真。 上文分析可知在所取的微元內(nèi)，應(yīng)變傳遞效率等于同長(zhǎng)度下光柵產(chǎn)生的應(yīng)變比基底產(chǎn)生的應(yīng)變，因此本文從傳感器中心取對(duì)稱(chēng)的長(zhǎng)10 mm，寬2 mm，厚1 mm 的長(zhǎng)方體基底建模，并且在截面沿軸向添加與整體相同的載荷。 可以確定，在粘接FBG 部分，模型基底產(chǎn)生的應(yīng)變與柱式傳感器實(shí)際的應(yīng)變一致。 模型的網(wǎng)格劃分如圖3 所示。 所用材料參數(shù)如表2 所示。

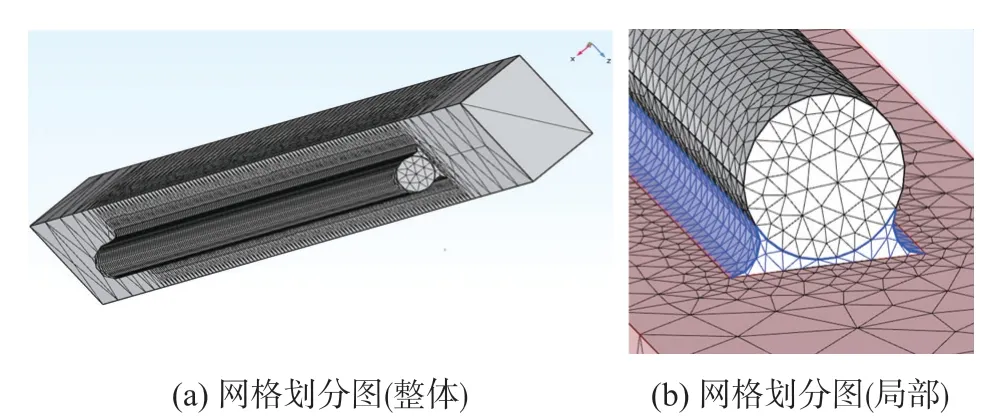
圖3 有限元模型

表2 仿真參數(shù)設(shè)置

圖4 是粘接層彈性模量對(duì)應(yīng)變傳遞效率影響的曲線圖，其中粘接層半徑R為0.2 mm。 可以看出，隨著粘接層彈性模量不斷升高，應(yīng)變傳遞效率逐漸增大，在彈性模量趨近于10 GPa 時(shí)，傳遞效率趨于平穩(wěn)，達(dá)到99%，隨后，傳遞效率緩慢下降。 圖5 是粘接層半徑R值對(duì)應(yīng)變傳遞效率的曲線圖，粘接層材料為環(huán)氧樹(shù)脂，可見(jiàn)，隨著粘接層半徑R逐漸增大，應(yīng)變傳遞效率緩慢降低。

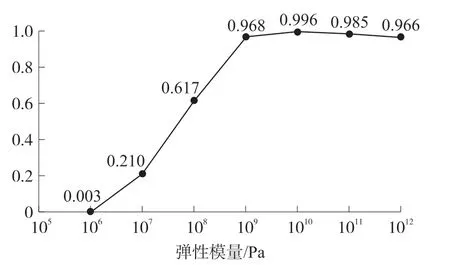
圖4 粘接層彈性模量對(duì)應(yīng)變傳遞效率影響

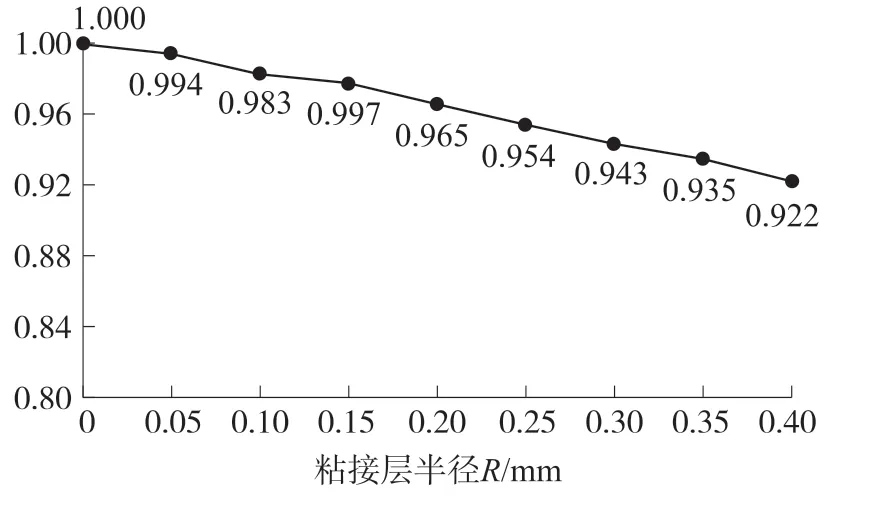
圖5 粘接層半徑R 對(duì)應(yīng)變傳遞效率的影響

3 實(shí)驗(yàn)驗(yàn)證

為了驗(yàn)證模型以及仿真的準(zhǔn)確性，我們對(duì)比了502 膠水和環(huán)氧樹(shù)脂610 對(duì)傳感器精度的影響，并對(duì)比了膠水厚度較薄、適當(dāng)、較厚等三種厚度對(duì)傳感器精度的影響。

3.1 實(shí)驗(yàn)工藝

在實(shí)驗(yàn)前，先用已經(jīng)非常成熟的全橋應(yīng)變計(jì)測(cè)試，驗(yàn)證柱體的基本性能，結(jié)果表示柱式傳感器的基本性能優(yōu)良，應(yīng)變變化均勻、無(wú)突變、精度高。 光柵的帶寬會(huì)影響信號(hào)輸出的質(zhì)量，過(guò)大會(huì)導(dǎo)致輸出光波變形，產(chǎn)生多個(gè)波峰，過(guò)小可能會(huì)導(dǎo)致解調(diào)儀采集不到反射光。 在反復(fù)調(diào)試下，本文選用反射率90%，帶寬0.2 nm 的布拉格光柵。

粘貼時(shí)使用標(biāo)準(zhǔn)器具，保證每次實(shí)驗(yàn)對(duì)光柵施加的預(yù)應(yīng)力都相同，并且使得粘接表面實(shí)況如示意圖所示。 實(shí)驗(yàn)時(shí)，在光柵外圈包裹一層聚氨酯發(fā)泡材料，以達(dá)到隔熱、隔空氣流動(dòng)的作用，減少溫度影響。

3.2 粘接層彈性模量對(duì)傳感器精度的影響

實(shí)驗(yàn)前，分別用502 膠水和環(huán)氧樹(shù)脂610 在柱式傳感器表面沿軸向粘貼好FBG。 在上表面沿軸向分別施加8 t、16 t、24 t、32 t、40 t 的壓力再依次遞減，測(cè)三次，總計(jì)3×9 個(gè)數(shù)，記錄數(shù)據(jù)后利用MATLAB 軟件處理并繪圖。 圖6 為502 膠水和環(huán)氧樹(shù)脂610 的直線擬合情況，由于兩條擬合直線較為接近，為了便于觀察，圖7 為圖6 放大后的擬合圖。圖中*和Δ 分別為610 環(huán)氧樹(shù)脂和502 膠水的原始點(diǎn)，實(shí)線和虛線分別是610 環(huán)氧樹(shù)脂和502 膠水的直線擬合圖。

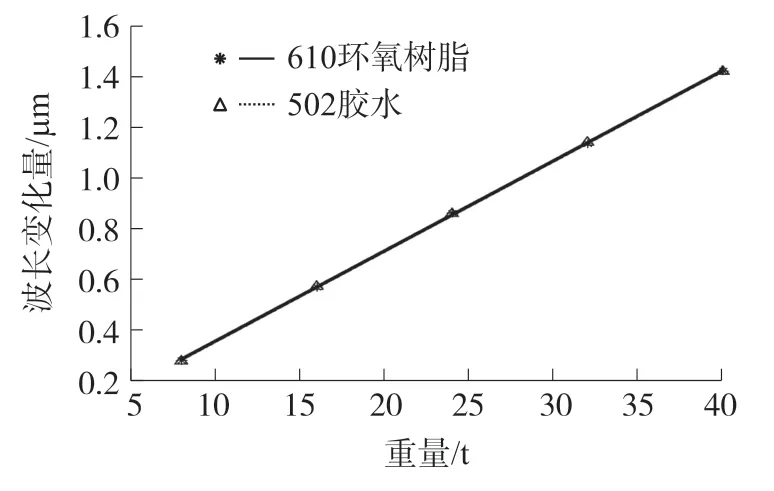
圖6 粘接層彈性模量擬合情況(整體)

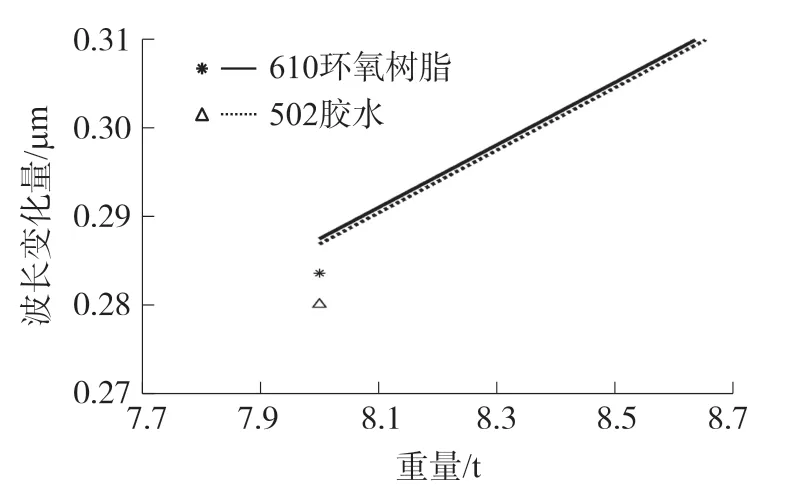
圖7 粘接層彈性模量擬合情況(局部)

可見(jiàn)環(huán)氧樹(shù)脂610 對(duì)數(shù)據(jù)的擬合程度更好，經(jīng)計(jì)算502 膠水作為粘接層時(shí)，傳感器的線性度L＝0.006 5，重復(fù)性R＝0.0076，遲滯H＝0.006 7。 環(huán)氧樹(shù)脂610 作為粘接層時(shí)，傳感器的線性度L＝0.005，重復(fù)性R＝0.004 5，遲滯H＝0.003 9。 可見(jiàn)粘接層彈性模量越大，傳感器的精度越高，特別是對(duì)傳感器的遲滯有非常大的提升。 這是由于彈性模量越大，三者之間的剪應(yīng)力越大，應(yīng)變傳遞效果越好。

3.3 粘接層厚度對(duì)傳感器精度的影響

將粘接層半徑按“較薄(0.1 mm)”、“適當(dāng)(0.2 mm)”、“較厚(0.3 mm)”三種粘接方式粘在柱式傳感器表面，按和3.2 節(jié)同樣的測(cè)試方法測(cè)試并處理數(shù)據(jù)。 下圖為三種粘接層半徑對(duì)應(yīng)直線的擬合圖，可以看出:當(dāng)粘接層半徑在0.2 mm 時(shí)，擬合度為98.4%，擬合效果最好。

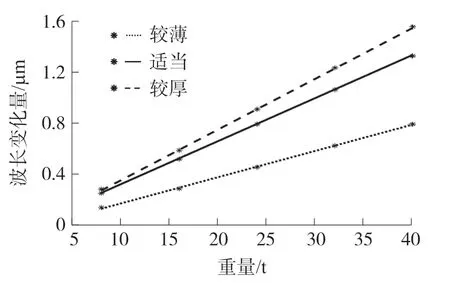
圖8 粘接層各厚度數(shù)據(jù)擬合情況

處理數(shù)據(jù)后得出在粘接層半徑“較薄(0.1 mm)”時(shí)，傳感器的線性度L＝0.011，重復(fù)性R＝0.008 9，遲滯H＝0.027；粘接層半徑“適當(dāng)(0.2 mm)”時(shí)，傳感器的線性度L＝0.004，重復(fù)性R＝0.007 3，遲滯H＝0.004 9；在粘接層半徑0.3 mm 時(shí)，傳感器的線性度L＝0.009 5，重復(fù)性R＝0.009 7，遲滯H＝0.067。

可以看出粘接層半徑“較薄”時(shí)，傳感器精度并不會(huì)最好，出現(xiàn)了仿真結(jié)果和實(shí)驗(yàn)結(jié)果不一致的情況。 原因是在建立數(shù)學(xué)模型時(shí)，我們假設(shè)基底、粘接層和光柵之間不會(huì)發(fā)生相對(duì)滑動(dòng)，但在實(shí)驗(yàn)中，粘接層過(guò)薄會(huì)引起三者之間發(fā)生相對(duì)滑動(dòng)，導(dǎo)致信號(hào)輸出不穩(wěn)定，這點(diǎn)可以從解調(diào)儀示數(shù)回彈觀察到。 通過(guò)實(shí)驗(yàn)，粘接層的最佳半徑R約0.2 mm，此時(shí)應(yīng)變傳遞效率最高，傳感器靈敏度最高。

4 結(jié)論

本文研究了粘接層參數(shù)對(duì)柱式傳感器應(yīng)變傳遞效率的影響，通過(guò)理論建模、有限元仿真和實(shí)驗(yàn)驗(yàn)證等方式得出了粘接層彈性模量和厚度半徑對(duì)應(yīng)變傳遞效率的影響，提供了控制柱式傳感器表面布拉格光柵應(yīng)變傳遞效率的幾個(gè)關(guān)鍵因素，給出了一般影響規(guī)律和具體數(shù)值，將傳感系統(tǒng)的精度提升到0.5%以內(nèi)。 并且有以下結(jié)論:①應(yīng)變傳遞效率和粘接層彈性模量基本成正相關(guān)，在109 Pa 時(shí)到達(dá)最高，隨后緩慢下降。 從工程力學(xué)角度講，彈性模量會(huì)影響粘接層和兩端的剪應(yīng)力，剪應(yīng)力正是使光柵產(chǎn)生應(yīng)變的原因。 ②在粘接層半徑R大于0.2 mm 后，隨著半徑R增大，應(yīng)變傳遞效率越低，但當(dāng)粘接層半徑小于0.2 mm 時(shí)，基底、粘接層和光柵之間可能發(fā)生相對(duì)滑動(dòng)，傳感器的精度下降。 但本文還未將更多參數(shù)加以討論，例如粘接層長(zhǎng)度、FBG 材料、基底的材料等，在后續(xù)的研究中，可以更全面的討論這些參數(shù)的影響。