在歸類中梳理提煉
——以教材中的一個面積模型圖的應用為例

揚州中學教育集團樹人學校（225000） 華板玉

數學知識是明確的、可列舉的，但對應的題又是大量的，是做不完的，這一點師生都深有感觸。有的學生雖然做了很多題目，可是題目稍微一變，就不知從何下手了，時常伴有迷茫、困惑、受挫的情緒，久而久之也就失去了數學學習興趣。那么如何應對這種現象，處理好量和質的辯證關系呢？筆者結合多年的教學實踐，深感解題是鞏固和應用所學知識的重要途徑，做一定數量的題目是必要的，除此之外，還要做一個解題有心人，善于將做過的題進行歸類，在歸類中梳理解題中所用到的知識點，提煉其中蘊含的思想方法。在歸類中梳理提煉，特別在中考階段性復習中，效果更為明顯。現以人教版教材中的一個面積模型圖的應用為例，就如何在歸類中梳理知識點、提煉思想方法進行探討。

一、面積模型圖的呈現

如圖1，直線l1∥l2，△ABC與△DBC的面積相等嗎？為什么？你還能畫出一些與△ABC面積相等的三角形嗎？

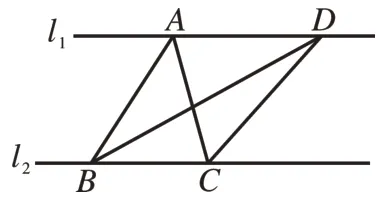
圖1

分析：此題是在學生學過平行四邊形的性質和兩條平行線之間的距離定義等知識之后給出的，它是三角形面積性質的延續。如圖2，根據“兩條平行線之間距離處處相等”的性質，可知△ABC的BC邊上的高AS與△DBC的BC邊上的高DT相等。根據“同底等高的三角形面積相等的性質，可得S△ABC=S△DBC。以此類推，可知當點E在直線l1上時，可得S△EBC=S△DBC=S△ABC。同理，可得△ADB與△ADC的面積相等（角度的切換）。

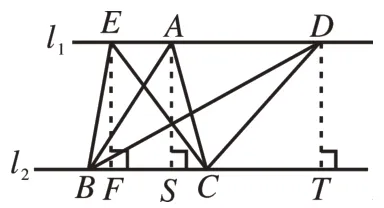
圖2

推論：如圖3，直線l1∥l2，點A，D在直線l1上，點B，C在直線l2上，AC，BD相交于點O，則△ABO與△CDO的面積相等。

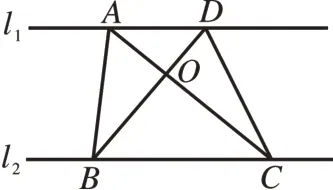
圖3

證明：∵直線l1∥l2，點A，D在直線l1上，點B，C在直線l2上，∴S△ABC=S△DBC，∴S△ABC-S△BOC=S△DBC-S△BOC，∴S△ABO=S△CDO。

點評：△ABO與△CDO面積相等，是兩條平行線間三角形面積的相等性與等式性質的“合力”。

從題設和證明中，我們可得到這樣的一個結論：兩條平行線間同底三角形的面積相等。它是兩條平行線性質的應用，是同底等高三角形面積相等性質的“衍生”。

二、面積模型圖的應用

兩條平行線間同底三角形的面積相等的圖形，可作為一個面積的模型圖，這一模型圖是隱藏在圖形中的，需要師生觀察圖形，從中發現這一模型圖，它為解決面積問題提供了一個巧妙的思路。在中考面積問題中，涉及這一模型圖的題目比較多，現列舉幾例。

（一）以網格為背景

［例1］如圖4 所示的網格是正方形網格，A，B，C，D是網格線交點，則△ABC的面積與△ABD的面積的大小關系為：S△ABC_____S△ABD（填“＞”“=”或“＜”）。

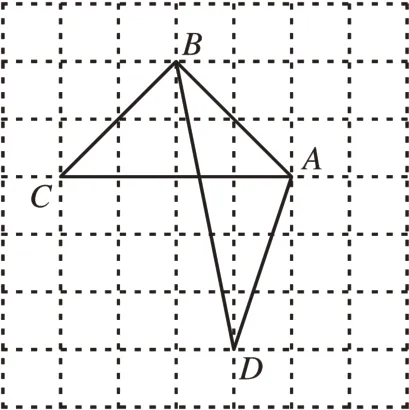
圖4

分析：網格邊長為1，網格中三角形的邊長都是可求的，同時網格線間還有垂直、平行的位置關系，充分利用網格的度量性和位置關系可求兩個三角形的面積。

解法1：根據網格邊長的度量性、垂直性可求得S△ABC；S△ABD雖不能直接求得，但可用兩邊分別為2、5 的矩形的面積減去3 個直角三角形的面積求得。綜上，可求得△ABC和△ABD兩個三角形的面積均為4，故填“=”。

解法2：網格中的網格線不僅平行或垂直，而且所構成的矩形的對角線平行或垂直，所構成的正方形的對角線平行或垂直，基于此，連接CD，會發現CD是邊長為3 的正方形的一條對角線，而AB又是邊長為2 的正方形的一條對角線，于是AB∥CD，而△ABC與△ABD恰是這兩條平行線之間底同為AB的三角形，所以這兩個三角形的面積相等。

點評：此題以網格為載體，比較兩個三角形面積的大小。對比兩種方法，前一種重計算，而后一種重觀察、重發現，省去了計算環節，顯然，后者更簡捷。而網格中兩條平行線之間的等積三角形的獲取不是顯現的，而是隱藏其間的，要連接CD這條輔助線才能顯現，這需要學生留心觀察、聯想思考。細品解法2，從中可梳理出的知識點有：兩條平行線間同底三角形面積相等，可提煉的思想方法有轉化思想，而實現轉化的途徑就是留心觀察。

類比應用：如圖5，在每個小正方形的邊長為1 的網格中，點A，B，C均在格點上，點D為小正方形一邊的中點。

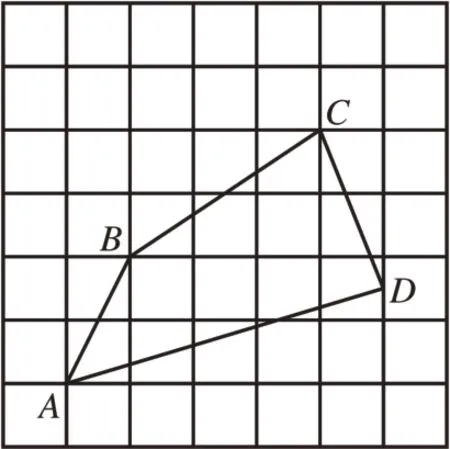
圖5

（1）AD的長等于______；

（2）請在網格中，用無刻度的直尺畫出一個點P，使其滿足S△PAD=S四邊形ABCD，并簡要說明點的位置是如何找到的（不要求證明）________。

分析：求AD長，需將AD“圈”在一個直角三角形中，用勾股定理求解；AC是四邊形ABCD的一條對角線，且這條對角線是直角邊都為4 的等腰直角三角形的斜邊，根據這一條件信息，可考慮作AC的平行線，構造平行線間的同底三角形。

解：如圖6，連接AC。取格點G，連接BG，交DC的延長線于點P，則點P為所求點。

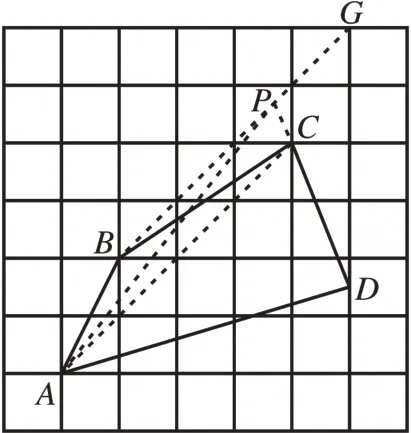
圖6

點評：求四邊形的面積，常需借助對角線將四邊形的面積轉化為三角形的面積之和。觀察網格，可知對角線AC是直角邊都為4 的等腰直角三角形的斜邊，根據這一特性，過點B作AC的平行線，將△ABC的面積轉化為△PAC的面積，而這一過程體現了平行線間同底三角形面積相等的性質，其間彰顯轉化思想的魅力。

例1 及“類比應用”的求解，都是依靠觀察，并尋找網格中的平行關系，從而提煉出等面積三角形。

（二）以圓為背景

［例2］如圖7，點O是半圓的圓心，BE是半圓的直徑，點A，D在半圓上，且AD∥BO，∠ABO=60°，AB=8，過 點D作DC⊥BE于點C，則陰影部分的面積是______。

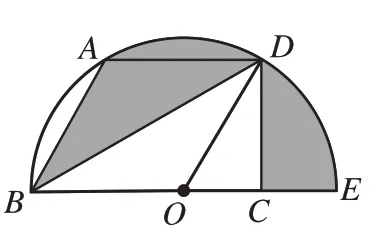
圖7

分析：本題的各部分陰影圖形是分散的，如何將所求圖形和待求圖形的面積有機組合在一起，如何將不規則圖形的面積轉化為可求的規則圖形的面積，是兩個思考點。

思考：根據AD∥BO這一條件，△ABD的面積可用哪一個三角形的面積等量替換呢？它體現了什么思想？

解：如圖8，連接OA。∵∠ABO=60°，OA=OB，∴△AOB是等邊三角形，∴OA=AB=8，∠AOB=60°，∴∠AOE=120°。∵AD∥OB，∴∠OAD=∠AOB=60°。∵OA=OD，∴△AOD是等邊三角形，∴∠AOD=60°，∠COD=60°。∵DC⊥BE，∴∠OCD=90°，∴∠CDO=30°，∴OC=OD=4，CD=∵AD∥OB，∴S△ABD=S△AOD，∴S△ABD+S弓形AD=S△AOD+S弓形AD，∴S△ABD+S弓形AD=S扇形AOD。∴S陰影=S扇形AOD+S扇形DOE-S△COD=S扇形AOES△COD=

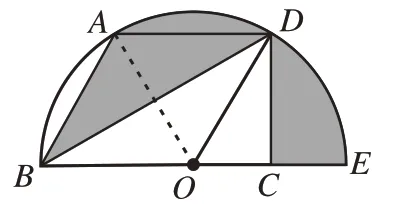
圖8

點評：此例以圓為背景，以平行為線索，根據“兩條平行線間的同底三角形面積相等”的性質，用△AOD的面積代替△ABD的面積，從而將不規則的△ABD與弓形AD的組合圖形面積轉換為可求的扇形AOD的面積，再進一步將陰影部分和△COD聯系在一起，通過面積的和差化得到所求。

回顧解題過程，用△AOD的面積替換△ABD的面積是開啟解題思路的一把鑰匙，也是平行線間同底三角形面積性質的靈活應用，體現了將不規則的圖形面積化為規則可求的圖形的面積的思想。此題涉及的知識點有：平行線間的等積三角形、等邊三角形的判定和性質、勾股定理、扇形面積公式，所涉及的思想方法有：等積轉換思想、整體思想、和差法等，實現這些思想方法的途徑為：觀察、聯想和整體性思維。

類比應用：如圖9，半圓的直徑AB=10，P為AB上一點，點C，D為半圓的三等分點，則陰影部分的面積等于____________。

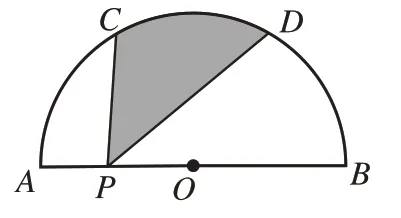
圖9

解：如圖10，連接CD，OC，OD，

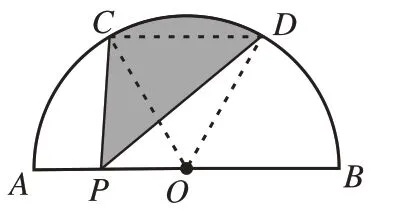
圖10

∵點C，D為半圓的三等分點，∴∠AOC=∠COD=∠BOD=60°，∴△COD為等邊三角形，∴∠OCD=60°，∴∠OCD=∠AOC，∴CD∥AB，∴S△PCD=S△COD，∴S陰影=S扇形OCD=

點評：證CD∥AB，進而得到S△PCD=S△COD是問題解答的關鍵所在，這又歸結到兩平行線之間同底三角形面積相等的性質。

（三）以正方形為背景

［例3］如圖11，正方形ABCD的邊長為2，點E在AB邊上。四邊形EFGB也為正方形，設△AFC的面積為S，則S=_____。

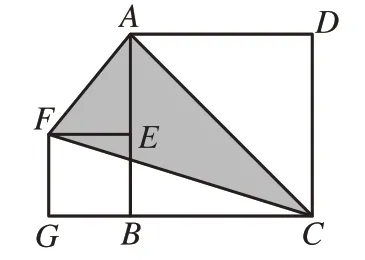
圖11

分析：所求三角形的面積只能計算出AC長，無法用三角形面積公式直接求得，能否用與其面積相等的三角形來直接替換呢？若不能直接替換，圖中的哪條線與AC平行呢？

解：如圖12，連接BF。∵四邊形ABCD為正方形，∴∠ACB=45°。∵四邊形BGFE為正方形，∴∠FBG=45°，∴∠FBG=∠ACB，∴BF∥AC。根據“兩平行線間同底三角形面積相等”的性質，得S△AFC=S△ABC=2。

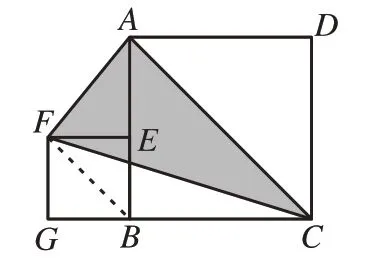
圖12

點評：此例以正方形為背景，連接正方形BGFE的對角線BF，會發現BF∥AC，根據“兩平行線間同底三角形面積相等”的性質，將△AFC的面積用△ABC的面積替換，從而將看似不可求的△AFC的面積求得。此題中的知識點有：正方形對角線的性質，兩平行線間同底三角形面積相等的性質，所蘊含的思想有轉化思想。

類比應用：正方形ABCD，正方形BEFG和正方形RKPF的位置如圖13 所示，點G在線段DK上，正方形BEFG的邊長為4，求△DEK的面積。

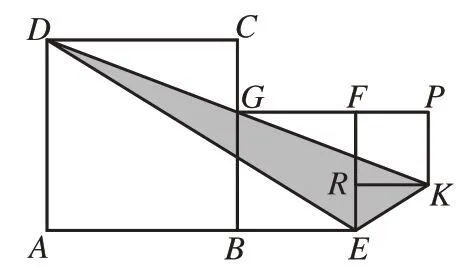
圖13

分析：三角形的面積不能直接求得，需要轉化。如何轉化呢？圖13 與圖11 都是“連體”正方形（有公共頂點，有公共邊），但圖13 中多出了一個小正方形。能否類比例3的思路呢？

解：如圖14，連接BD，EG，FK，易證BD∥EG∥FK，

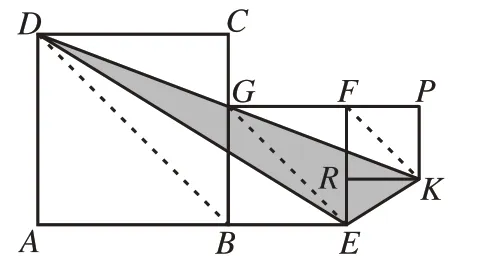
圖14

由BD∥EG，得S△DEG=S△BEG，

由EG∥FK，得S△KEG=S△FEG，

∴S△DEG+S△KEG=S△BEG+S△FEG，即S△DEK=S正方形BEFG=42=16。

點評：結果很“驚奇”（所求三角形的面積正好是圖13 中間正方形的面積），此例的解答類比了例3 的解題思路，注重正方形對角線的平行位置關系的提取和應用，以及兩條平行線之間同底三角形面積相等的性質的應用。注重與基礎題（例3）的類比，有助于開啟學生的解題思路。

三道例題及其變式應用題都分別從不同“背景”展示了兩條平行線之間同底三角形面積相等的性質，也就是說，拋開背景的因素，可歸為一類題。通過對三道題中知識點的梳理，得到了它們中所含有的相同知識點：兩條平行線之間同底三角形面積相等。解完題后若草草了事，則這個知識點的價值就得不到充分體現，更談不上解題中蘊含的思想方法（側重轉化思想）的挖掘，以及思想方法實現的途徑（觀察與聯想）的體驗。

題是解不完的，解題之后不僅要梳理出相關知識點，還要去體驗題目背后蘊含的思想方法，并進行挖掘、提煉與遷移，這樣才能提升解題質量，取得事半功倍的效果。