用超級畫板輔助初中函數教學的設計

江蘇蘇州工業園區東延路實驗學校（215000） 陳 莉

數形結合是函數教學的主要方法。在具體實踐中，靜態性地展示函數圖像，學生無法詳細觀察到函數圖像的由來。而使用超級畫板，以動態的形式呈現函數圖像及其幾何性質，能讓學生在與超級畫板交互的過程中完成對新知識的理解，提升學生的學習效率。

一、發揮超級畫板動態演示功能，設計函數教學

以人教版教材九年級上冊“函數的圖像和性質”中的“y=a(x-h)2+k”教學為例，使用超級畫板的動態演示功能，對函數的過程性知識與原理性知識進行教學設計。

（一）教學目標

知識與技能目標：經過本課學習，學生可精準繪制二次函數圖像。

過程與方法目標：經過作圖與探究，學生可掌握y=a(x-h)2+k的圖像特點和性質，學會應用數形結合法。

情感態度與價值觀目標：在教師引導下，學生經歷觀察、推理、交流等學習過程，獲得解決問題的方法，并在交流中總結經驗，提高數學學習效率。

（二）內容分析

y=a(x-h)2+k二次函數圖像和性質是人教版教材九年級上冊中的內容。本節課先借助二次函數頂點式，引導學生作出函數圖像，然后觀察函數圖像。

（三）學情分析

在此之前，學生已經學習了y=ax2函數的圖像和性質，從學生對過程性知識與原理性知識的學習情況來看，其對函數圖像與性質的掌握并不理想，實際應用也存在問題。

（四）教學過程

1.回顧交流，以舊促新

活動1：請指出以下哪些函數是二次函數。

（1）y=

（2）y=-5x2；

（3）y=3x-4；

（4）y=-2x2+x；

（5）y=-3(x+2)2-2。

設計意圖：幫助學生回憶二次函數的相關知識，為引出新知打好基礎。

活動2：利用描點法繪出下列函數的簡圖，并指出函數的開口方向、對稱軸、頂點坐標和最值。

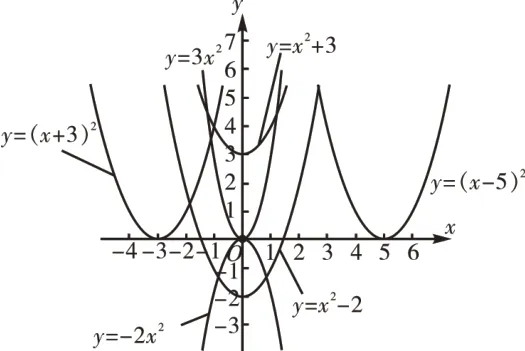
圖1

（1）y=-2x2，y=3x2；

（2）y=(x-5)2，y=(x+3)2；

（3）y=x2+3，y=x2-2。

設計意圖：一是幫助學生回顧描點法作圖的基本步驟，培養學生的畫圖能力，讓學生意識到常規描點作圖法不僅耗時，而且容易出錯，為引出超級畫板做好鋪墊；另一方面讓學生經歷畫圖的過程，初步探究y=ax2、y=(x-h)2和y=x2+k這三類不同函數的基本性質，感知三種不同類型函數的異同。

活動3：利用描點法繪制圖像，說一說每道題目中的兩個函數圖像之間有什么關系。

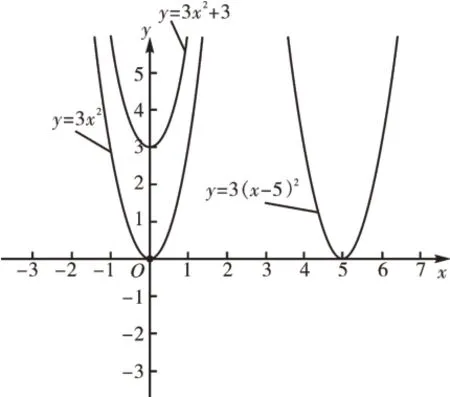
圖2

（1）y=3x2與y=3x2+3；

（2）y=3x2與y=3(x-5)2。

設計意圖：進一步強化學生對函數圖像“平移”的認知。

2.創設情境，觀察類比

活動4：利用超級畫板繪制下列函數的圖像（如圖3）。

圖3

（1）y=x2；

（2）y=(x-1)2；

（3）y=(x-1)2+1。

觀察函數圖像，認真填寫表1。

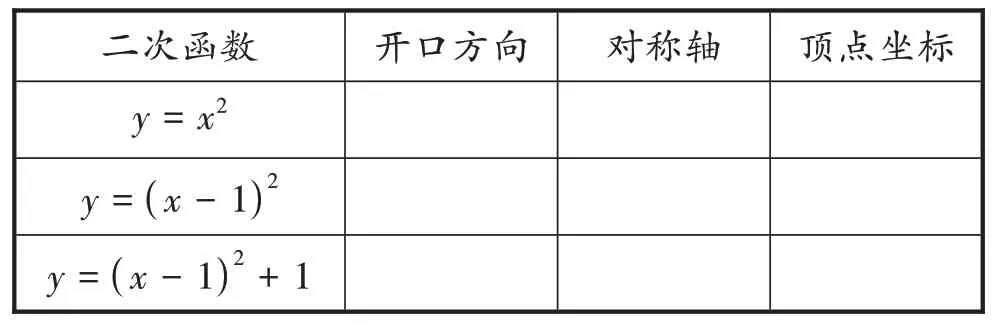
表1

活動5：利用超級畫板繪制下列函數的圖像（如圖4）。

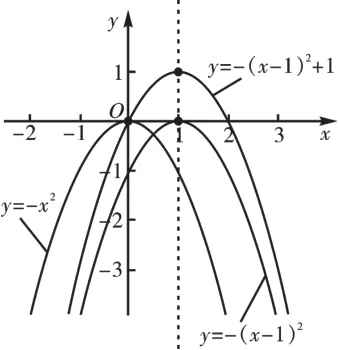
圖4

（1）y=-x2；

（2）y=-(x-1)2；

（3）y=-(x-1)2+1。

觀察函數圖像，認真填寫表2。

表2

設計意圖：一是比較兩種作圖，讓學生感受到超級畫板的便利性和精準性；二是讓學生進一步經歷類比的過程，感知不同類型函數圖像的異同。

3.問題驅動，深化認知

活動6：下面兩組函數能否通過平移使圖像重合？

（1）y=x2，y=(x+1)2，y=(x+1)2+1；

（2）y=-x2，y=-(x+1)2，y=-(x+1)2+1。

活動7：用超級畫板動態演示平移上面兩組函數圖像，使其重合。

活動8：通過對活動6 和活動7 的總結，小組討論y=a(x-h)2+k的圖像的特點、形狀、開口方向、對稱軸、頂點坐標，結合超級畫板作圖，填寫表3。

表3

設計意圖：讓學生通過小組探究，結合超級畫板完成對表格內容的填寫，幫助學生梳理二次函數的圖像和性質。

4.成果展示，認知升華

活動9：對活動8的學習成果進行收集與整理，找出存在的普遍問題，結合超級畫板動態演示y=a(x-h)2+k函數圖像的變化過程。

設計意圖：通過對學生學習成果的收集與分析，了解學生的探究程度和準確性；結合超級畫板的動態演示，幫助學生糾正錯誤認知，讓學生更加直觀地發現二次函數圖像的變化規律。

活動10：通過超級畫板的展示，讓學生再次在教師的帶領下，歸納與總結y=a(x-h)2+k的性質，以幫助學生檢驗小組探究成果的正確性。

圖5

一般地，拋物線y=a(x-h)2+k與y=ax2的形狀、大小相同，只是位置不同，將拋物線y=ax2的函數圖像向上（下）、向左（右）進行平移，就能得到y=a(x-h)2+k的函數圖像，平移的方向和距離由h，k所決定。

（1）當a＞0 時，二次函數圖像的開口朝上；當a＜0時，二次函數圖像的開口朝下；

（2）對稱軸是x=h；

（3）頂點坐標為(h,k)。

設計意圖：通過師生互動，回顧與總結二次函數圖像的性質，幫助學生構建正確、完整的知識體系，加深學生對知識的理解和記憶。

活動11：學生自由回答問題。

（1）在平移二次函數y=a(x-h)2+k圖像的過程中，三個參數a，h，k分別起到了什么作用？

（2）二次函數圖像的平移具有什么規律？

（3）運用超級畫板輔助學習，你有什么發現？

設計意圖：引導學生嘗試用自己的語言歸納與整理本節課所學的知識內容。

5.遷移運用，鞏固練習

設計分層作業，通過知識的遷移運用和強化鞏固，促使不同層次學生都獲得不同程度的發展。

（1）基礎層。不畫圖，直接說出下列函數的開口方向、對稱軸及頂點坐標。

①y=-3x2；

②y=-3(x+1)2+5；

③y=(x+1)2+1；

④y=-(x-4)2-1。

設計意圖：設計基礎層題目，主要考查學困生對本節課重點知識的掌握程度，促使他們對二次函數的圖像有一個全面的認識。

（2）提高層。函數y=-3x2的圖像經過怎樣的平移得到函數y=3(x+1)2+5的圖像？

設計意圖：設計提高層題目，目的是強化學生對二次函數平移問題的認知和理解。

（3）拓展層。已知A(-2,y1)，B(3,y2)和C(4,y3)是二次函數y=-(x-1)2+4 圖像上的點，請你判斷y1，y2，y3的大小。

設計意圖：設計拓展層作業，目的是綜合考查學生對二次函數圖像和性質的掌握程度及靈活運用能力，促進學生知識遷移能力的培養。

二、超級畫板教學功能的開發與運用

（一）開發的目標

上述教學過程中多次運用了超級畫板，每次運用超級畫板都是為了完成一次小的教學目標，然后總結歸納，確定二次函數y=a(x-h)2+k的圖像和性質。隨著教學過程的推進，設置的目標分別為：

1.借助超級畫板繪制下列函數的圖像：（1）y=x2；（2）y=(x-1)2；（3）y=(x-1)2+1。

2.借助超級畫板繪制下列函數的圖像：（1）y=-x2；（2）y=-(x-1)2；（3）y=-(x-1)2+1。

3.借助超級畫板探究函數y=a(x-h)2+k的圖像和性質。

4.借助超級畫板探究二次函數圖像的平移特性。

5.借助超級畫板感知參數的變化對y=a(x-h)2+k函數圖像的影響。

（二）運用的方式

二次函數頂點式的圖像和性質的教學更加適合動態呈現，教師借助超級畫板的動態演示功能，直接展示教學內容，在教師的講解下，便于學生學習與思考。教學過程的交互性設計，可讓師生在超級畫板中進行交互，可以是教師講解，學生操作，也可以是學生自己借助超級畫板進行探索。學生經過反復的觀察與實踐，由認識y=ax2的圖像逐漸向認識y=a(x-h)2+k的圖像擴展。

（三）畫板的運用

運用超級畫板，第一，用描點法畫出最基本的y=ax2的圖像，在畫板中列表，即輸入任何一個x值后，對應的y值就會發生改變，先列出5 組（x，y）的值，然后描點，點擊畫板上的按鈕，手動確定五個點的x值和y值，最后連線，可使用兩種連線方法，即手動作圖與直接呈現。可在開始的時候先讓學生手動作圖，即用鼠標沿著y=ax2圖像的軌跡移動跟隨作畫，待學生熟悉圖形后，就可采用直接呈現圖像的方法。第二，畫出y=a(x+h)2和y=a(x-h)2的圖像，將其與y=ax2的圖像作比較，可以在同一坐標系中使用不同顏色展示，如紅色表示y=a(x+h)2的圖像，藍色表示y=a(x-h)2的圖像、黑色表示y=ax2的圖像。頁面中設計兩個按鈕，如紫色表示向左平移一個單位長度，綠色表示向右平移一個單位長度。此時確定y=ax2的圖像，向左點擊一下，觀察其變化，然后向右點擊兩下，通過這種軌跡的追蹤，幫助學生更好地理解h的意義，同時培養學生的想象能力與抽象能力。第三，比較y=ax2的圖像與y=a(x-h)2-k的圖像，在同一直角坐標系中畫出紫色與紅色的圖像，以黑色為平移痕跡。學生在觀察后可在a、h、k值中輸入隨意數字，會發現只要有一個值發生改變，就會生成新的圖像。觀察后讓學生依次點擊左右平移、上下平移、初始化的按鈕，進行逐一演示與分析，讓學生明白每次圖像的改變與什么值有關，引導學生深入感受二次函數中不同值的意義。

三、函數教學中超級畫板的運用建議

首先，超級畫板的運用要精致化。如果一味地運用超級畫板，就會出現喧賓奪主的情況。超級畫板的運用要精致化，不能濫用，應選擇適合的功能進行教學，否則學生會出現不愛思考的情況。

其次，應將超級畫板與其他教學手段相結合。雖然超級畫板功能強大，但應盡量不只使用這一種輔助教學形式，要多使用其他教學形式，以多種手段相輔相成促使教學效率的提升。

最后，應結合教學實際情況運用超級畫板。并不是所有的教學環節都適合運用超級畫板，教師需深入研究教學大綱，并根據自己的教學經驗，視情況運用超級畫板。