構造正方形 化歸熟悉圖形妙解題

?蘇州工業(yè)園區(qū)東沙湖實驗中學 倪明慧

1 引言

正方形是一種特殊的四邊形，遇到問題，若能熟練運用正方形的判定定理，合理構造正方形，活用正方形的性質(zhì)，往往會收到意想不到的解題效果.

2 構造的方法與途徑

2.1 正方形與形外等邊三角形

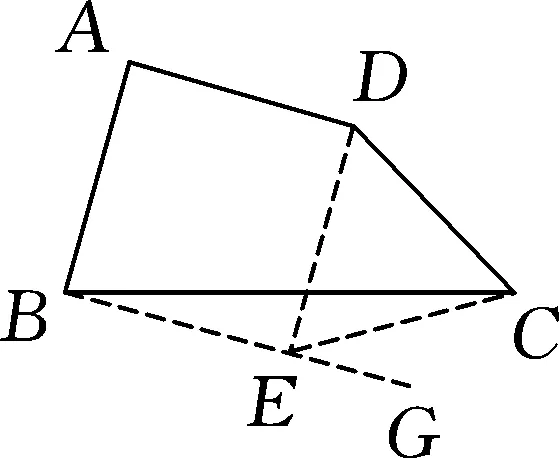
圖1

例1四邊形ABCD中，∠BAD=90°，∠ADC=150°，且AB=AD=DC.求∠ABC的度數(shù).

分析：通過構造垂線的方法，在AB的右側構造邊長為AB的正方形，從而把不熟悉的計算問題，轉(zhuǎn)化為正方形背景下的計算問題，找到了方法，明確了知識，確定了思路，解答自然水到渠成.

解：如圖1，過點B作BE⊥AB，垂足為B，過點D作DE⊥AD，垂足為D，直線BE，DE交于點E，連接EC.

∵∠BAD=∠ABE=∠ADE=90°，

∴四邊形ABED是矩形.

∵AB=AD，

∴四邊形ABED是正方形.

∴∠BED=90°，AB=AD=BE=DE.

∵∠ADC=150°，AB=AD=DC，

∴DC=DE，∠EDC=60°，即△DCE是等邊三角形.

∴EC=DE=BE，∠DEC=60°，∠BEC=150°.

∴∠EBC=15°.

∴∠ABC=∠ABE-∠EBC=90°-15°=75°.

點評：運用鄰邊相等的矩形是正方形構造正方形，這是解題的關鍵.運用正方形的性質(zhì)，融合已知，巧用含有60°角的等腰三角形是等邊三角形，把問題轉(zhuǎn)化為正方形與形外以正方形邊為邊的等邊三角形問題，化陌生為熟悉，提高解題效率.

2.2 正方形與旋轉(zhuǎn)模型

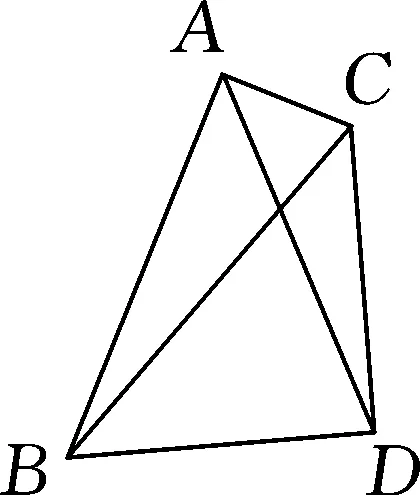
圖2

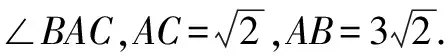
分析：通過構造垂線的方法，把計算問題背景轉(zhuǎn)化為正方形背景下的旋轉(zhuǎn)計算型問題.用好旋轉(zhuǎn)的性質(zhì)、正方形的性質(zhì)，成為解題的關鍵.

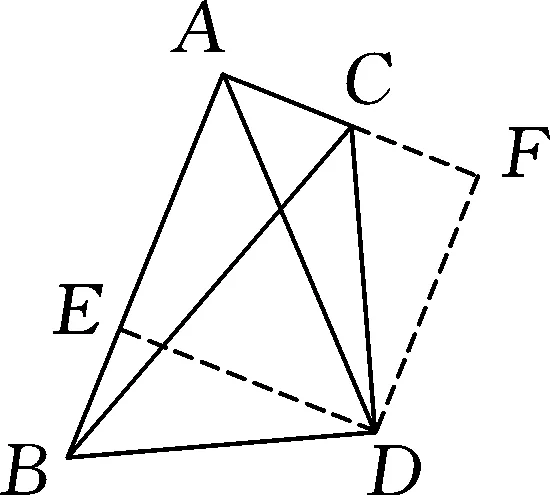
圖3

解：如圖3，過點D作DE⊥AB，垂足為E，過點D作DF⊥DE，與AC的延長線交于點F.

∵∠BAF=∠AED

=∠EDF=90°，

∴四邊形AEDF是矩形.

∵AD平分∠BAC，

∴DE=DF，四邊形AEDF是正方形.

∴∠AFD=90°，AE=ED=DF=FA.

∵∠BDC=90°=∠EDF,

∴∠BDE=∠CDF.

∴△BDE≌△CDF.

∴BE=CF.

∵AE=FA，

∴AB-BE=AC+CF.

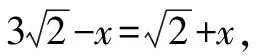
點評：以兩個直角為正方形的一組對角，運用構造垂線方法生成四邊形，運用鄰邊相等的矩形是正方形構造正方形，這是解題的關鍵.構造正方形的同時生成一對旋轉(zhuǎn)90°即可全等的直角三角形模型，利用三角形全等性質(zhì)、正方形的性質(zhì)、方程思想，可以使得問題順利求解.這種構造正方形的方法值得熟練掌握.

2.3 正方形半角模型

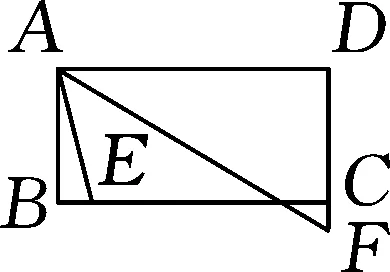
圖4

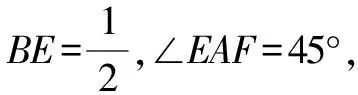
分析：通過構造垂線的方法，把計算問題背景轉(zhuǎn)化為正方形背景下的半角模型計算問題.用好半角模型、正方形的性質(zhì)，成為解題的關鍵.

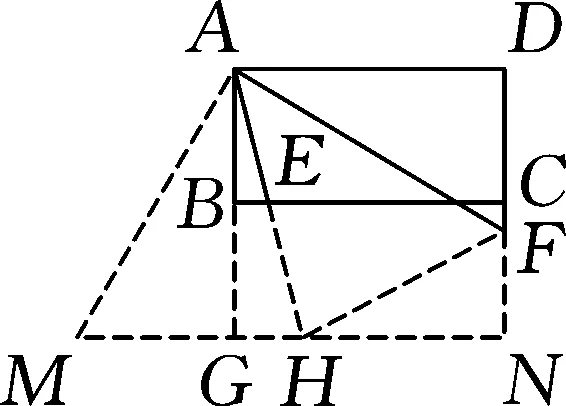
圖5

解：如圖5，延長AB至點G，使AB=BG=2，延長DC至點N，使DC=CN=2，連接GN，延長AE交GN于點H.

∵四邊形ABCD是矩形，AG=AD=4，

∴四邊形AGND是正方形，四邊形BGNC是矩形.

延長NG至點M，使MG=DF.

∵∠ADF=∠AGM=90°，AD=AG，MG=DF,

∴△ADF≌△AGM，AM=AF，

∠GAM=∠DAF.

∵∠EAF=45°，

∴∠DAF+∠GAH=45°.

∴∠GAM+∠GAH=45°，即∠MAH=∠HAF=45°.

∴△AMH≌△AFH.

∴MH=HF=DF+GH.

∴BE是△AGH的中位線，GH=1.

設DF=x，則

HF=x+1，NH=GN-GH=3，

FN=DN-DF=4-x.

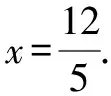
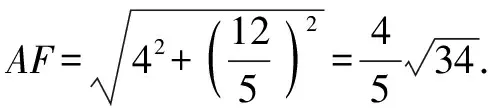
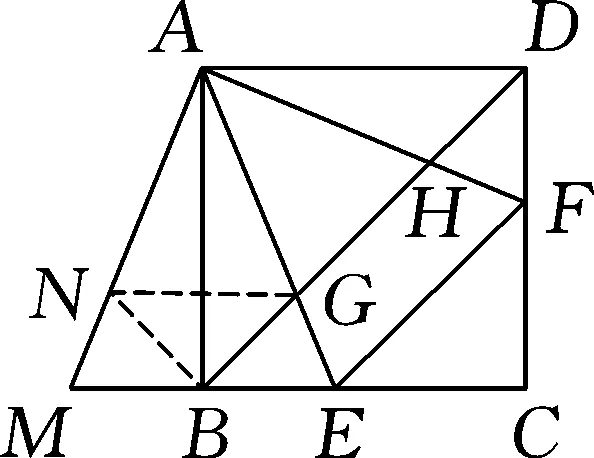
圖6

點評：通過構造正方形，矩形背景下的問題轉(zhuǎn)化為正方形背景下的半角模型，從而靈活運用三角形的全等、三角形中位線定理、勾股定理將問題步步破解.構造正方形成為解題的關鍵和基礎，熟練掌握正方形的半角模型圖是解題的核心和根本.除了常見結論，半角模型還有如下一個新結論，也要熟練掌握.如圖6，半角模型的一個新結論BG2+DH2=GH2.感興趣的讀者可以嘗試解答.

2.4 正方形與形內(nèi)等邊三角形

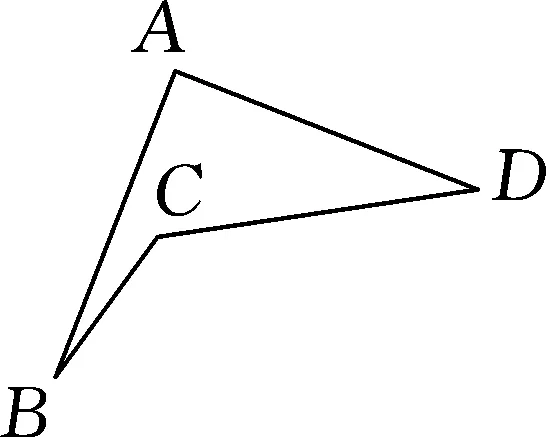
圖7

例4如圖7，已知∠A=90°，∠D=30°，且AB=AD=DC.求∠B的度數(shù).

分析：通過構造垂線的方法，把計算問題背景轉(zhuǎn)化為正方形和形內(nèi)等邊三角形計算型問題.用好等邊三角形及正方形的性質(zhì)，成為解題的關鍵.

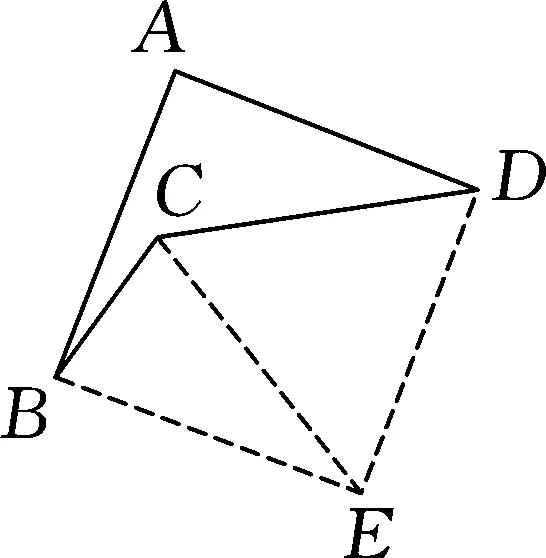
圖8

解：如圖8，過點B作BE⊥AB，垂足為B，過點D作DE⊥AD，垂足為D，兩線交于點E，連接EC.

∵∠BAD=∠ABE

=∠ADE=90°，

∴四邊形ABED是矩形.

∵AB=AD，

∴四邊形ABED是正方形，∠BED=90°，

AB=BE=ED=DA.

又∵DC=AD,∠ADC=30°,

∴∠CDE=60°，△DCE是等邊三角形.

∴EC=EB，∠DEC=60°，∠BEC=30°.

∴∠EBC=∠ECB=75°.

∴∠ABC=∠ABE-∠EBC=90°-75°=15°.

點評：運用鄰邊相等的矩形是正方形構造正方形，把問題轉(zhuǎn)化為正方形與形內(nèi)以正方形邊為邊的等邊三角形的問題，這種構造正方形的方法值得熟練掌握.

3 解后反思

通過問題的探究，可以積累如下幾條解題經(jīng)驗：

(1)靈活運用已知條件，根據(jù)正方形的判定構造，運用構造垂線法、分割圖形法、倍長短邊法，把不規(guī)則圖形構造成正方形，從而把一般背景下的問題求解轉(zhuǎn)化為正方形背景下的問題求解，靈活運用正方形的性質(zhì)，往往能找到更有效的求解思路；

(2)常態(tài)數(shù)學學習中要注意積累教材典型習題、例題的模型圖，熟練掌握圖形的基本構架、基本條件、基本結論、基本特點，必要時化歸到這個模型圖上，這也是一種高效求解方法；

(3)養(yǎng)成良好的模型思想，熟記常見、常用的幾何模型，運用靈活的手段把問題轉(zhuǎn)化為模型求解，這也是高效解題的基本途徑之一，熟練駕馭靈活運用模型思想是良好數(shù)學素養(yǎng)的體現(xiàn).Z