建模以靜制動問題情境 發展數學基本思維方法
——以“動點問題專題”團隊教研為例

?江蘇省如皋市丁堰鎮初級中學 黃曉蘭

1 引言

陽春三月，春暖花開，又是一年初中畢業生緊張的備考階段，九年級數學學科組成員個個摩拳擦掌，投身到為學生沖刺中考做好服務的工作行列.學科組教師分組分專題編寫導學案，再由學科教研組集體通過，對備考的前期工作做好了規劃.筆者帶過幾屆畢業班，因此，義不容辭承擔了初中數學備考中難啃的骨頭——涉及動點問題的專題.本次學科組教研的重點就是研究“動點問題專題”的導學案，筆者是這次教研活動的中心發言人.以下是本次教研活動的一些做法和要點記錄.

2 精心規劃專題類型，擬好幫助學生系統備考的導學案

在中考試題中，“動點問題”通常以圖形中存在一個或多個動點在某線段或曲線上運動為載體，試題開放性強.這類問題解決方法的切入點是找到特殊點，再通過相關的數學知識靈活解決問題.

研討片段1：

筆者：“動點問題”的解題關鍵是以靜制動、動中求靜.因為它涵蓋了諸多的數學思想，如分類、轉化、方程與函數、數形結合等，試題突出了對幾何圖形中動點運動變化的考查.我認為要做好以下三點：

(1)以教材涉及的三角形、四邊形、函數圖象等圖形為載體，在不同的層面和不同的運動變化方式中讓學生學會“動點問題”的數學思維方法，體會圖形性質及圖形變化是基礎，空間觀念和合情推理是思維方法的數學建模過程.

(2)幫助學生打好解決圖形在動點運動到不同的特定位置時的基礎，以此作為計算推理的突破口，從而感悟、觀察、分析圖形變化的思考方法.

(3)“以不變應萬變”是解決數學“動點問題”最有效的思維方式，它蘊含了動態幾何的核心問題，幫助學生形成分類、轉化、方程與函數、數形結合等數學思想，是備考的重要目標.

教師甲：從你擬定的導學案初稿可以看到，近年來考查的主要內容有點動、線動和圖形動幾種形式.我認為這只是對動態的理解，能不能對題目的知識體系進行分類呢？

教師乙：“動點問題”專題用題目的知識體系進行分類，更便于對問題情境的建模，導學案調整為這種形式更好.

教研反思：對同一專題的分類有不同的方法，筆者采用的是對近年來各省市中考中出現的熱點進行分類，即點動、線動和圖形動這三種形式，沒有很好地突出知識體系，而是通過題目進行甄別，是考慮到備考復習需要綜合運用知識的緣故.其他教師提出需要改進，筆者認為他們提出的建議有道理.可能是筆者對學情估計不準確的緣故.

研討片段2：

筆者：現在我將專題的題目重新分為兩大類，一是動點問題中的函數關系類，二是動點問題中以動態幾何為主線的壓軸題類.然后分成子類型，大家認為怎么樣？

教師丙：這樣分類知識的系統性更強，有利于幫助學生對“動點問題”進行建模.

組長：這種方法比較好，與去年的做法大同小異.現在請大家將導學案的草稿進行相對應的調整.調整好之后，哪位教師再說說你在這兩個類型下設立的子類型目標？

教師丁：函數關系類和動態幾何為主線的壓軸類都可以按草稿中的點動、線動和圖形動的形式進行相應的分類.

組長：大家有沒有其他建議？如果沒有，那么，現在可以通過電腦將導學案的草稿進行調整.

筆者重新規劃導學案.

教研反思：眾人拾柴火焰高.的確，經過調整后的導學案知識的系統性更強，比開始的草稿中由點動、線動和圖形動的形式為主線(分三個學時完成)，再分為函數關系法的思想和幾何推斷法的思想進行轉化，思路更明了.教學相長，這樣調整導學案，可以將例題分為兩個課時，然后鞏固提升為一個課時.

3 精心挑選典型例題，擬好幫助學生進行數學建模的思路

例題對學生解決實際問題起到了引領和示范的作用，還可以很好地幫助學生進行智力訓練.專題中的例題既是學生獲取數學知識的重要途徑，也是在解題過程中，獲得技能技巧的關鍵渠道.因此，在備考專題教學中精心挑選典型例題，充分發揮其鞏固數學概念、運用法則或性質、規范解題格式等作用，使學生養成良好的數學思維品質，確保在中考時會做的題一分不丟.

研討片段3：

筆者：按照各位同仁的建議，現在將此專題分為兩大類.第一類是“動點問題”函數關系法的思想，再細分為三個小類.其中第一小類用函數的思想解決“點動”問題，例題選用的是2019年山東省臨沂市中考數學模擬試卷中的第14題.

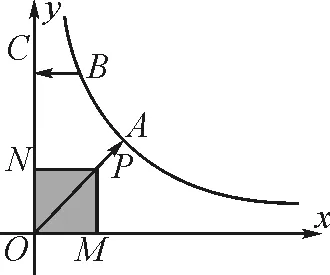
圖1

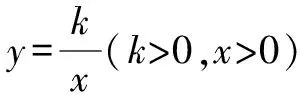
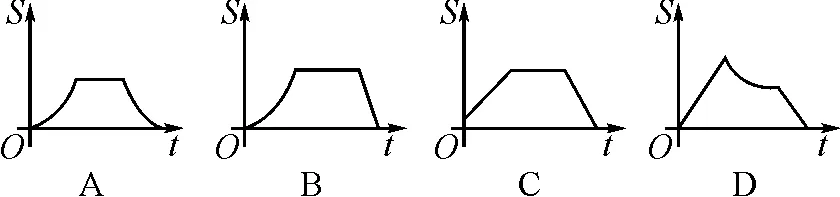
圖2

筆者選本題的原因是此題主要涉及了反比例函數的定義、圖象、性質、解析式，以及反比例函數的應用等，考查學生的綜合分析和應用能力.關于這些知識點，可以在課堂教學過程中進行歸檔.

筆者給出下列一些解題方法，幫助學生對類似的問題情境進行建模：

(1)若證明的線段在某一四邊形中，則利用特殊四邊形(如例1中是矩形，其面積為點P的坐標的積等)的性質，通過量的轉化、等量代換進行求證；

(2)若證明的線段在某個三角形中，則利用等腰、直角三角形的性質(如勾股定理、三角形的面積是兩直角邊積的一半等)進行求證；

(3)若證明的線段在兩個三角形中，則通過三角形全等的判定及性質進行證明；

(4)若出現三條線段的數量關系，則需要轉化為兩條線段進行探究.

教師乙：例1選擇的是2019年山東省臨沂市中考數學模擬題，能否找一道本省地市級近年的中考試題？

教師丙：我選了2020年江蘇省無錫市中考數學試卷第28題，略有改動，大家看看怎么樣.

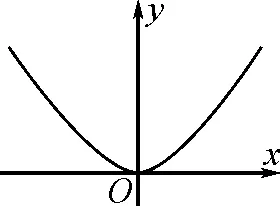
圖3

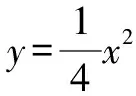
(1)若點P的縱軸坐標是m，點A的橫坐標為8.

①用含m的代數式表示點M的坐標.

②點P能否落在該二次函數的圖象上？若能，求出m的值；若不能，請說明理由.

(2)當m=2時，若動點P恰好落在該二次函數的圖象上，請直接寫出此時滿足條件的所有直線OA的函數表達式.

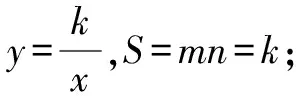
4 寫在最后

總之，對中考備考專題進行團隊教研，教師針對自己負責的專題進行深入理解與設計.在活動中，通過導學案的草案研究教什么、練什么、怎樣教、怎樣練.同時，導學案以電子文稿的形式呈現，教師個人補充自己在教學實踐中的思考，以及具體的、不同的做法.通過學科組團隊的教研活動，可以充分發揮每個人的智慧，挖掘每個人的潛能，節省時間，形成合力，從而打造復習備考的高效課堂.