追本溯源 注重基礎
——從“分式”中考題的原型說起

?甘肅省天水市秦州區汪川中學 王進賢

1 引言

“分式”作為初中數學代數部分的內容，在日常教學、階段檢測、中考中都是非常重要的知識點和命題點[1].基于此，本文中從幾道比較典型的中考題出發，采用尋找原型題的方法回歸到課本基礎內容中，進一步和廣大一線教師再學習和再認識“分式”.

2 中考試題重現

縱觀這幾年的中考試卷，每一年都有“分式”題的出現，這充分說明“分式”是中考的命題熱點[2].如下面的幾道中考題：

①(2020年貴陽)當x=1時，下列分式沒有意義的是( ).

A.±1 B.0 C.-1 D.1

從這幾道中考題不難看出，“分式”作為考點基本上呈現在以下幾個方面：

首先，分式有意義的條件，如2020年貴陽等中考題.

其次，分式化簡，如2020年浙江湖州等中考題.

再次，分式化簡求值——確定值代入.這一類多出現在選擇題和填空題中，但近幾年出現的較少.

第四，分式化簡求值——自選值代入.這類比較普遍，如2020四川雅安、2019通遼等中考題.

最后，分式值為0的條件，如2019貴港等中考題.

3 回到課本，尋找原型

根據前述，中考題的原型大多出自課本，所以本文以北師大版教材為參考，在課本中尋找這些中考題的原型.

原型一：北師大版教材第109頁隨堂練習1(1)(2)和例1(2).

例1當x取什么值時，下列分式有意義？

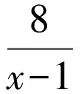
反思：分式有意義和無意義的區分非常簡單，只需觀察分母是否能為零.當分母為零時，分式無意義；當分母不為零時，分式有意義[3].這類問題要注意兩種形式.一種分母無需因式分解，如原型一的例1(1)，只需直接由分母不等于零求出結果；另一種分母需因式分解，如原型一的例1(2)，這種需先因式分解，然后由ab≠0得到a≠0且b≠0.

原型二：北師大版教材第109頁的隨堂練習2和例1(1).

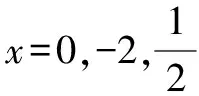
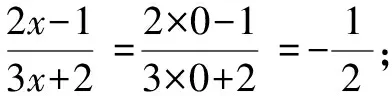
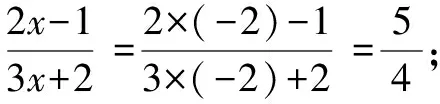
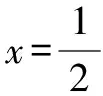
反思：這類分式求值問題相對比較簡單，只需將給出的字母的值直接代入即可.但在計算的過程中需注意幾個地方.首先，含負號的字母或數字代入時需放入小括號中；其次，計算需仔細認真，有必要認真檢查.

原型三：北師大版教材第113頁習題5.2第2(1)題.

例3化簡下列式子并求值:

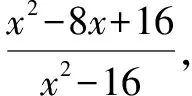
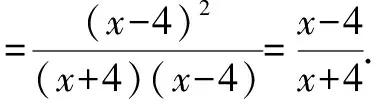
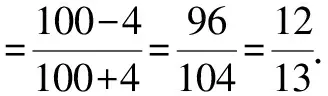
反思：化簡類問題是中考“分式”部分的“常客”，要順利解決這類問題，學生需牢固掌握因式分解的方法[4].所以，在掌握分式的有關問題時，有必要同時復習因式分解有關內容.

原型四：北師大版教材第113頁習題5.3第2(1)(2)題.

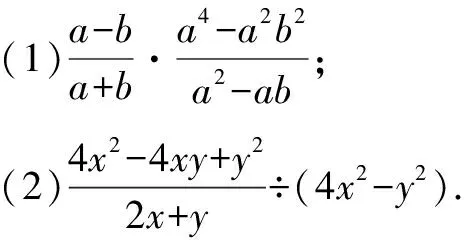
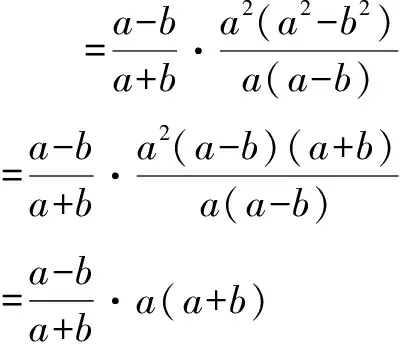
=a(a-b).

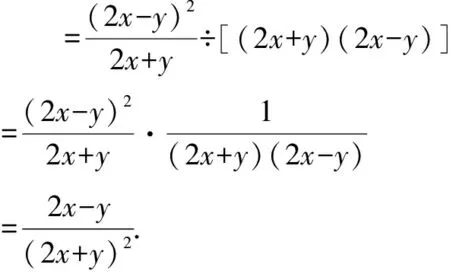
反思：與原型三一樣，解決這類問題的關鍵仍在于因式分解.需注意的是，在處理除法時，應轉換為乘它的倒數.

4 經驗交流與分享

為了達到比較理想的教學效果，筆者在教這一單元時采用了一些方法，現分享如下：

首先，分式新授課和因式分解復習同步.從以上原型題及其解題過程可以看出，牢固掌握因式分解是順利解決這類問題的關鍵.所以，筆者在分式新授時，將因式分解的復習同步進行.

其次，培養學生檢查的習慣.這類問題的計算量較大，字母、數字、運算符號比較多，需要學生特別注意檢查.筆者要求學生打草稿時在稿紙中間書寫“要檢查”三個字，并待學生檢查完后將這三個字打勾，用以提醒學生檢查.

5 結語

綜上所述，教師一方面要認識到因式分解與分式有千絲萬縷的聯系，同時要用各種方法讓學生牢固掌握因式分解及與分式有關的基礎知識，借此為后期掌握好分式方程及與之有關的知識奠定基礎.