挖“教材”之本 體“源題”之活*
——從一道幾何證明題談起

?江蘇省南通市海門區(qū)海南中學(xué) 朱愛平

1 引言

本文中以人教版八年級下冊第十八章“平行四邊形”第69頁的第14題為例，分析如何挖掘教科書上的習(xí)題，通過設(shè)置階梯問題引導(dǎo)學(xué)生進行深度思考分析，利用圖形變式提升學(xué)生遷移能力.通過一題多變、一題多解，有意識地引導(dǎo)學(xué)生從“變”的現(xiàn)象中發(fā)現(xiàn)“不變”的本質(zhì)，從不變的本質(zhì)中探究“變”的規(guī)律，培養(yǎng)學(xué)生的探索精神和創(chuàng)新意識，提高學(xué)生數(shù)學(xué)核心素養(yǎng)，給予學(xué)生帶得走的知識.

2 原題呈現(xiàn)

如圖1，四邊形ABCD是正方形，點E是邊BC的中點，∠AEF=90°，且EF交正方形外角的角平分線CF于點F，證明：AE=EF.(提示：取AB中點G，連接EG.)

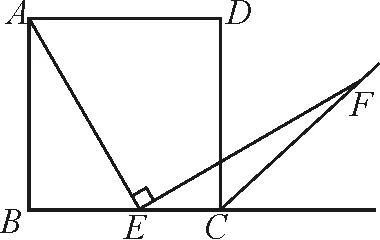
圖1

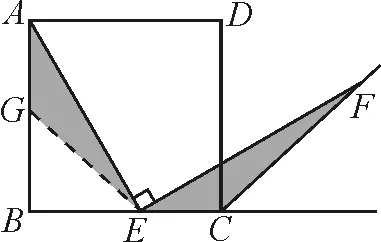
圖2

3 分析引導(dǎo)

思路分析：從結(jié)論需要證明AE=EF出發(fā)，聯(lián)想到可證明全等，觀察圖形需要構(gòu)造全等，由條件點E是BC的中點聯(lián)想取AB的中點G.如圖2，證明△AGE≌△ECF.根據(jù)練習(xí)后面給予的提示，學(xué)生能夠自行解決此問題.但如果僅僅停留在表層問題的解決，那真是入寶山而空手回了.

引導(dǎo)1：點E是BC的中點這個條件是否可以修改呢？

學(xué)生容易想到：點E為BC上任意一點.

引導(dǎo)2:如果點E為BC上任意一點，其余條件不變，如圖3，那么AE=EF還成立嗎？

引導(dǎo)3：動手畫一畫，探究一下.此時在構(gòu)造全等時，還是取AB的中點G嗎？你是怎么取的？為什么這樣取呢？

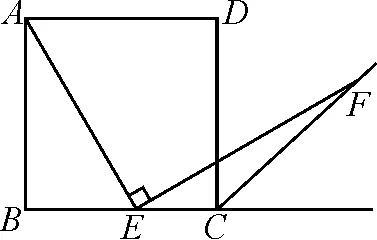
圖3

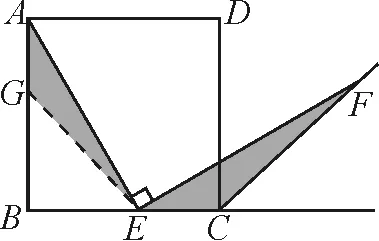
圖4

這樣的變式問題，學(xué)生能夠遷移方法，還是會去構(gòu)造△AGE≌△ECF(如圖4)，則需要AG=EC.所以在AB上截取AG=EC,連接EG，在證明∠AGE=∠ECF=135°時，需要根據(jù)等式性質(zhì)證明BG=BE，所以在作輔助線時，也可以在AB上截取BG=BE，再去證明.

設(shè)計意圖:通過畫圖簡單的變化，鍛煉學(xué)生的畫圖……