多維度研究三角形內部長度問題

?四川省鄰水中學 林冰雁

1 問題呈現

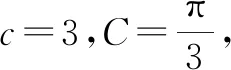
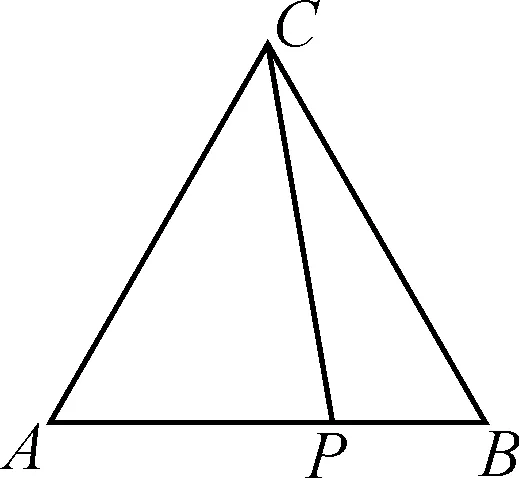
圖1

2 問題分析

此題以銳角三角形為背景，已知一角C及其對邊AB，和對邊上一點P，求三角形內部線段CP所在邊的最大值.選取正確的角度作為解題的切入點是關鍵的一步.根據題目所給的信息，從已知出發，利用“正弦定理與余弦定理[1]”進行簡單計算，而長度的最值問題容易涉及到“三角函數和向量[2]”、函數與方程等知識，其中的變形與推理精彩絕倫.還可利用直線的參數方程中t的幾何意義輕松解決該問題.最后巧妙結合“圓[3]”的性質并進一步建立平面直角坐標系，將坐標法與三角函數相結合，實現知識的貫穿性.

3 解法探究

3.1 思維視角一：邊化角思維

解法1：在△BCP中，由余弦定理可得

CP2=a2+1-2acosB.

(顯然，|CP|跟a和角B都有關系，但是無法直接求得最大值，進一步思考邊a能否化成角B呢？)

在△ABC中，利用正弦定理可知

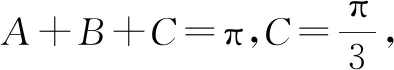
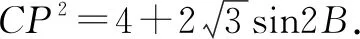
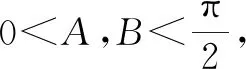
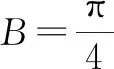
點評：解法1比較典型，其主要思路是先利用余弦定理將CP2表示出來，以正弦定理作為橋梁，將邊a轉化成同一個角B，進一步結合題意確定該角的范圍，接著利用三角恒等變換將CP2轉化為三角函數模型，最后借助三角函數的性質求得最大值.

那還有其他的方法嗎？線段的長度即向量的模，解三角形通常與向量的知識相聯系.向量法是指根據題意選擇合適的基底，將所求線段用向量表示出來，利用平面向量基本定理和運算法則解題，將幾何問題轉化為向量運算問題，轉換了解題的方向.

3.2 思維視角二：向量思維

解法2：如圖2，過點P作BC的平行線……