成蘭鐵路軟巖隧道大變形控制技術及變形控制基準研究

郭小龍，譚忠盛，喻 渝

(1.北京交通大學 土木建筑工程學院， 北京 100044；2.中鐵二院工程集團有限責任公司，四川 成都 610031)

高地應力軟巖條件下擠壓型大變形控制是目前隧道及地下工程領域面臨的重要難題，國內外學者對此開展大量研究和實踐，取得了豐碩的研究成果[1]。在支護理論方面，形成了軸變理論[2]、聯合支護理論[3]、弧板支護理論[4]、松動圈理論[5]、主次承載區支護理論[6]、關鍵部位耦合支護理念[7]等。從支護理念上可分為剛性支護和柔性支護兩大類，剛性支護包括高強弧板、提前施作大剛度二襯、重型拱架、鋼管混凝土拱架等，柔性支護包括讓壓錨桿[8]、可縮性拱架[9-10]等。

隨著大變形隧道實踐工程的不斷推動，發現單一的控制措施往往難以奏效，為此出現眾多大變形聯合控制措施，包括開挖方法、地應力調整、支護體系、變形控制標準等，進而形成復雜的變形控制技術。如烏鞘嶺隧道采用斷面形狀優化、加大預留變形量、多重支護及加大襯砌剛度的支護結構，同時開挖方法上采用以實現快速封閉的短臺階及超短臺階法[11-12]；蘭渝鐵路出現大量擠壓型大變形隧道，包括木寨嶺隧道[13]、兩水隧道[14]、毛羽山隧道[15]等，其中尤其以木寨嶺隧道變形最為嚴重，提出導洞應力釋放，多層圓形支護，長錨桿(索)，注漿加固的綜合變形控制方案，同時提出了大變形控制分級管理理論和施工控制標準。隨著大變形隧道圍巖擠壓程度不斷提高，變形控制技術研究也逐漸從單一工況向考慮不同擠壓程度的變形控制體系進行完善[16-17]。

從上述分析可以看出，雖然目前針對軟巖隧道大變形控制技術已經從單一控制措施向多種措施聯合應用發展，同時向不同大變形等級的變形控制體系逐漸完善。但目前來看大變形控制理念不明確，缺乏針對不同大變形等級，適用性強的軟巖隧道大變形控制體系。

隧道變形控制基準是實現隧道信息化施工的重要基礎，又是提高隧道施工安全性、經濟性的重要手段[18]。尤其軟巖隧道變形量大，變形速率快，如果預留變形量不足，即使圍巖變形得到控制，依然會導致拆除支護、進行擴挖的后果[19]。隨著新奧法的推廣應用，國內外學者對隧道變形規律及控制基準進行了廣泛研究。文獻[20]認為通過大剛度支護控制深埋軟巖隧道變形不僅不科學而且經濟性差，應有一定的變形釋放，其預留變形量約為20～30 cm。趙東平等[21]通過現場量測數據分析，基于一定保證率，建立了大斷面黃土隧道預留變形量。王明年等[18]基于變形數據分析，提出了大斷面海底隧道CRD法絕對位移控制基準。我國的鐵路隧道設計規范中考慮隧道跨度、埋深、開挖方法等因素，對常規圍巖分級條件下隧道預留變形量及變形控制基準進行了詳細規定，但對于軟巖隧道如何通過監控量測數據反饋分析得到變形控制基準未給出明確解答。因此許多學者采用理論分析[22]、數值計算[23-24]、模型試驗[25-26]及現場試驗[27-28]等方法對軟巖隧道預留變形量及變形控制基準進行了研究。上述關于軟巖隧道變形控制基準的研究中，大多以隧道預留變形量作為主要研究對象，未考慮基于施工過程的隧道變形特征建立變形控制基準。同時考慮大變形分級，針對不同變形控制體系，系統性建立軟巖隧道變形控制基準的研究較少。

本文以成(都)蘭(州)鐵路典型軟巖隧道工程為依托，基于大量工程實踐，提出成蘭鐵路軟巖隧道大變形控制理念及變形控制體系。同時對大量變形量測數據進行統計分析，考慮施工過程中變形發展規律，建立軟巖隧道變形控制基準。

1 工程概況

成蘭鐵路為國鐵Ⅰ級雙線電氣化鐵路，采用客貨共運，設計時速200 km/h，線路最小曲線半徑為3 500 m，最大坡度9‰。

線路起于成都，向北經松潘、九寨溝接入蘭渝鐵路的哈達鋪站。線路總長457 km，隧道總長332 km，占路線總長度的73%，其中53%的隧道段落穿越軟巖地層。路線位于印度板塊與歐亞板塊相互碰撞縫合帶附近，地質構造復雜，構造運動強烈，穿越龍門山斷裂帶，西秦嶺斷裂帶和岷山斷裂帶，路線走向與主要構造帶位置關系見圖1。軟巖地層主要為千枚巖、板巖，巖體強度低，整體性差，在高構造應力作用下擠壓明顯，極易造成隧道大變形[29-30]。

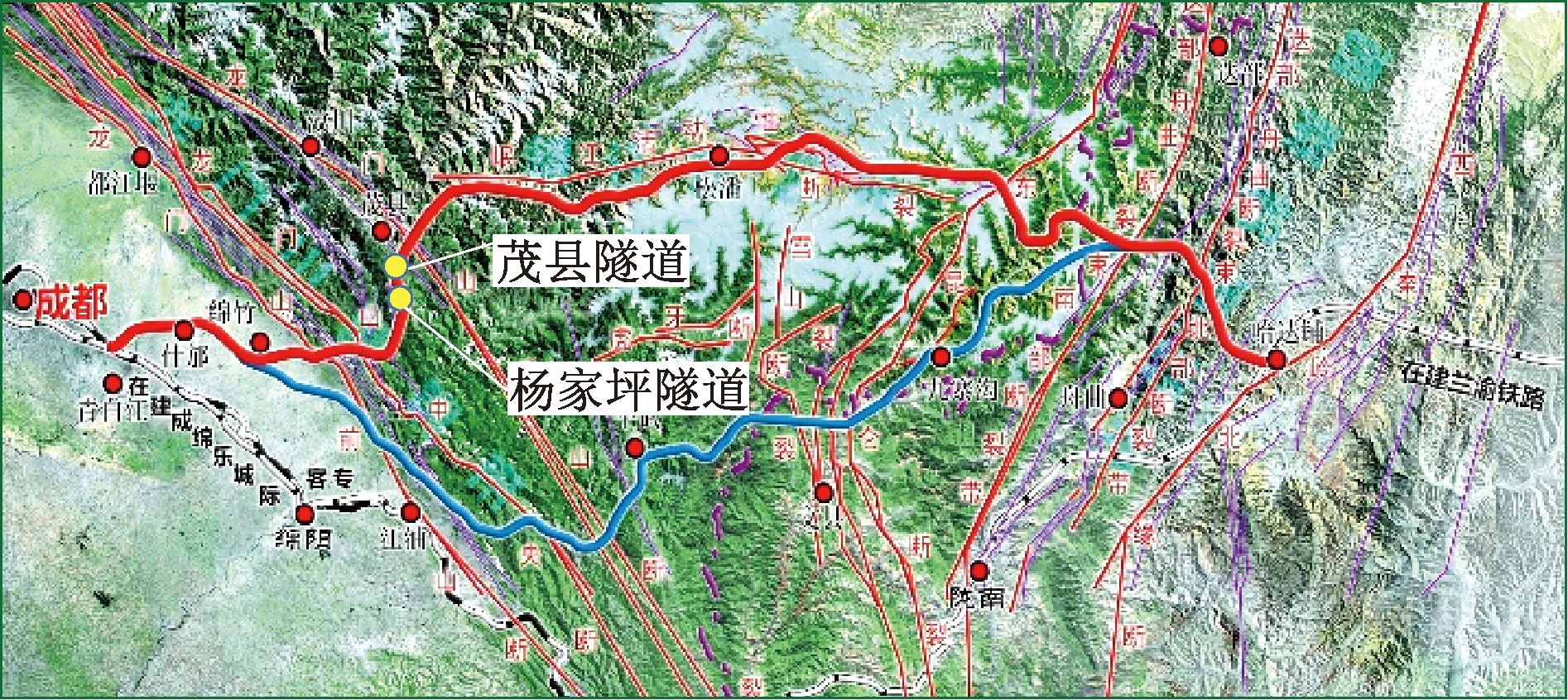
圖1 成蘭鐵路走向及主要地質構造

本文以發生典型大變形的楊家坪隧道和茂縣隧道為研究對象。楊家坪隧道全長12.84 km，最大埋深約718 m。茂縣隧道全長10.01 km，最大埋深約1 656 m，兩隧道通過核桃溝雙線大橋相連。兩隧道軟巖段圍巖主要為志留系茂縣群千枚巖，受龍門山后山斷裂帶影響，巖體破碎，巖石單軸抗壓強度為0.46～2.86 MPa[31-33]，隧道開挖后巖石粉化現象嚴重。

2 大變形控制理念及大變形分級

2.1 大變形控制理念

目前國內外軟巖大變形隧道工程實踐中存在多種變形控制理念，包括“以抗為主”“抗放結合”“主動控制”等。

“以抗為主”是指通過大剛度初期支護(單層或多層)控制圍巖變形，當圍巖變形持續發展時提前施作大剛度二次襯砌以抵抗圍巖變形。上述思路在實踐過程中均有成功及失敗案例。通過調研分析認為，“以抗為主”的理論成功控制圍巖變形的案例多以輕微大變形等級為主，在實施過程中甚至體現出施工成本相對較低，施工效率高的優點。但隨著圍巖擠壓程度不斷提高，大變形等級不斷增大，不少工程出現了二次襯砌開裂問題。因此，隨著大變形等級增大，目前的控制體系不能承受極高的應力荷載，“以抗為主”的大變形控制理論難以取得成功[34-35]。“抗放結合”是指針對軟巖隧道施工過程中對圍巖變形進行適度釋放，但圍巖變形的釋放需通過支護結構進行有效約束[19]。

隨著對軟巖隧道變形因素及變形機制認識的不斷加深，逐漸認識到常規的被動提供支護功能的支護體系無法有效提高圍巖的穩定性，不能達到“圍巖支護圍巖”的效果。因此，對于軟巖隧道應采用“主動控制”理念，以改善圍巖的應力狀態為核心，減少對圍巖擾動的同時主動加固圍巖，充分發揮圍巖的自承能力。

2.2 大變形分級標準

對隧道大變形進行分級，進而采用針對性措施，既可有效控制大變形，又可以節約成本[36-37]。Hoek等[38]提出了無支護條件下強度應力比與相對變形量的關系曲線，建立了被廣泛采用的大變形分級標準。此外眾多學者對大變形分級方法及標準進行了研究，分級指標多采用強度應力比和相對變形量，還包括初始地應力、絕對位移、彈性模量及綜合系數等[39-41]。成蘭鐵路隧道工程基于大量實測數據，考慮一定支護抗力，形成大變形分級標準[42]，見表1。

表1 成蘭鐵路隧道大變形分級標準

3 成蘭鐵路軟巖隧道大變形控制技術

基于上述“主動控制”理念，成蘭鐵路提出“優化斷面，強化錨桿、減少開挖分步，動態調整，分級控制”的軟巖隧道大變形控制技術。

基于大變形分級，逐步優化隧道斷面，提高支護結構的整體受力性能，又避免開挖空間的過度浪費。針對軟巖隧道變形速率快的特點，選擇合理的錨桿類型與參數，提高施工效率，及時發揮作用控制圍巖變形。同時盡量減少開挖分步，輕微大變形段采用二臺階帶仰拱法，中等大變形段采用二臺階法，嚴重與極嚴重大變形段采用三臺階法，施工過程嚴格控制臺階長度，初期支護盡早封閉成環，從而及時為圍巖提供支護抗力。通過加深地質工作，探明隧址區的地應力及巖體強度特征，結合已開挖段變形特征，采用動態設計的手段，及時調整大變形等級，采取相應措施[43]。

結合成蘭鐵路軟巖隧道大變形控制實踐，對上述變形控制措施進一步說明。

3.1 斷面優化

施工期間針對成蘭鐵路典型軟巖隧道進行了地應力測試，包括茂縣隧道、楊家坪隧道、柿子園隧道、松潘隧道、榴桐寨隧道等。測試結果表明成蘭鐵路隧址區地應力場類型為σH>σh>σv型，以水平應力為主。如楊家坪隧道最大水平主應力(σH)平均值為21.86 MPa，最小水平主應力(σh)平均值為11.51 MPa，垂直應力(σv)為8.81～9.98 MPa，水平側壓力系數達2.19～2.48。茂縣隧道最大水平主應力為25.99 MPa，最小水平主應力為20.00 MPa，水平側壓力系數為1.58[44-46]。成蘭鐵路隧址區以構造應力為主，邊墻位置受構造應力的強烈擠壓作用，邊墻變形顯著，支護結構極易造成彎曲變形破壞。單線鐵路隧道“瘦高型”斷面形式對邊墻變形及應力控制不利，同時仰拱較大矢跨比也不利于結構受力。雖然圓形斷面整體受力效果更好，但空間利用率低，施工成本高[37]。因此，基于大變形分級，考慮結構受力和施工成本，逐漸增大隧道邊墻曲率，增大仰拱矢跨比，從而改善結構受力，控制隧道變形，見圖2、圖3。圖中S、L分別為仰拱的計算關系矢高、計算跨度。

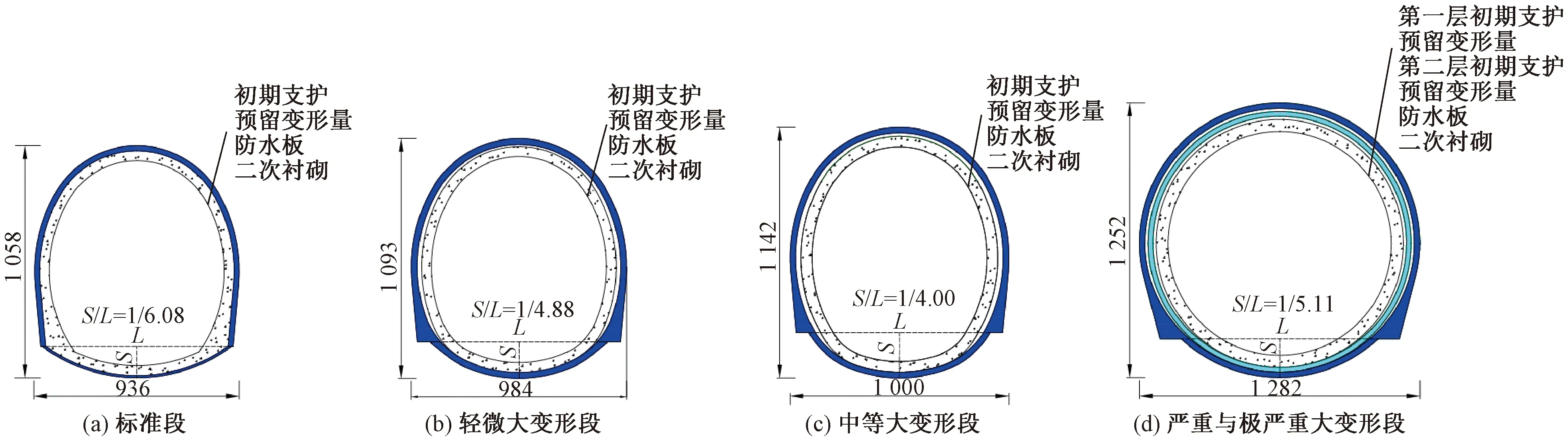
圖2 單線隧道支護結構斷面示意(單位：cm)

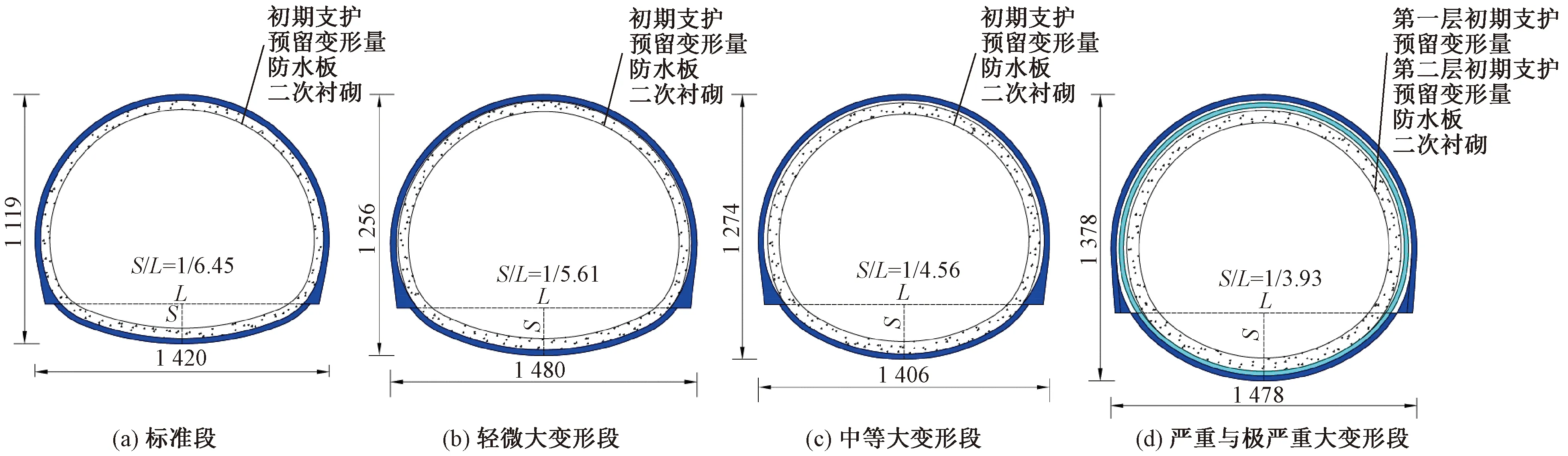
圖3 雙線隧道支護結構斷面示意(單位：cm)

3.2 錨桿支護技術

錨桿作為主動控制技術的重要組成部分，在控制軟巖隧道大變形方面具有重要作用[36]。為充分發揮錨桿的主動控制作用，成蘭鐵路在軟巖隧道錨桿形式、支護參數、施工機械、作用效果等方面進行了研究。

3.2.1 錨桿類型分析

目前錨桿形式眾多，受力原理及作用效果存在顯著差別。端錨式錨桿雖然施作簡單，技術成熟，但由于軟巖隧道圍巖強度低，難以產生足夠的錨固力。軟巖隧道由于圍巖松軟、強度低、有明顯的塑性變形，圍巖可能產生沿錨桿的流動變形，因此，這類巖體應采用全長黏結式錨桿[19]。

此外，由于軟巖隧道錨桿成孔困難，鉆孔深度大，導致灌漿效率低，施工質量差，因此傳統的砂漿錨桿適應性較差。自進式中空錨桿鉆、錨一次成型，同時通過中空桿體進行壓力注漿，不僅可以提高錨桿的施工效率，而且保證施工質量。因此成蘭鐵路軟巖大變形隧道優先選用自進式中空錨桿。

3.2.2 錨桿支護參數

一般認為錨桿長度主要取決于圍巖松動圈厚度，錨桿應穿透松動圈。因此為了充分發揮錨桿主動控制圍巖變形的作用，結合圍巖松動圈測試結果，對錨桿參數進行優化[34]。

采用聲波法和地質雷達法開展了圍巖松動圈值測試，測點布置見圖4。嚴重大變形段圍巖波速隨深度變化規律見圖5，1#測點由于難以進行保水耦合，未測得圍巖波速。取邊墻圍巖松動圈平均值，最終圍巖松動圈測試結果見表2[42]。

圖4 聲波法測點布置示意(單位:m)

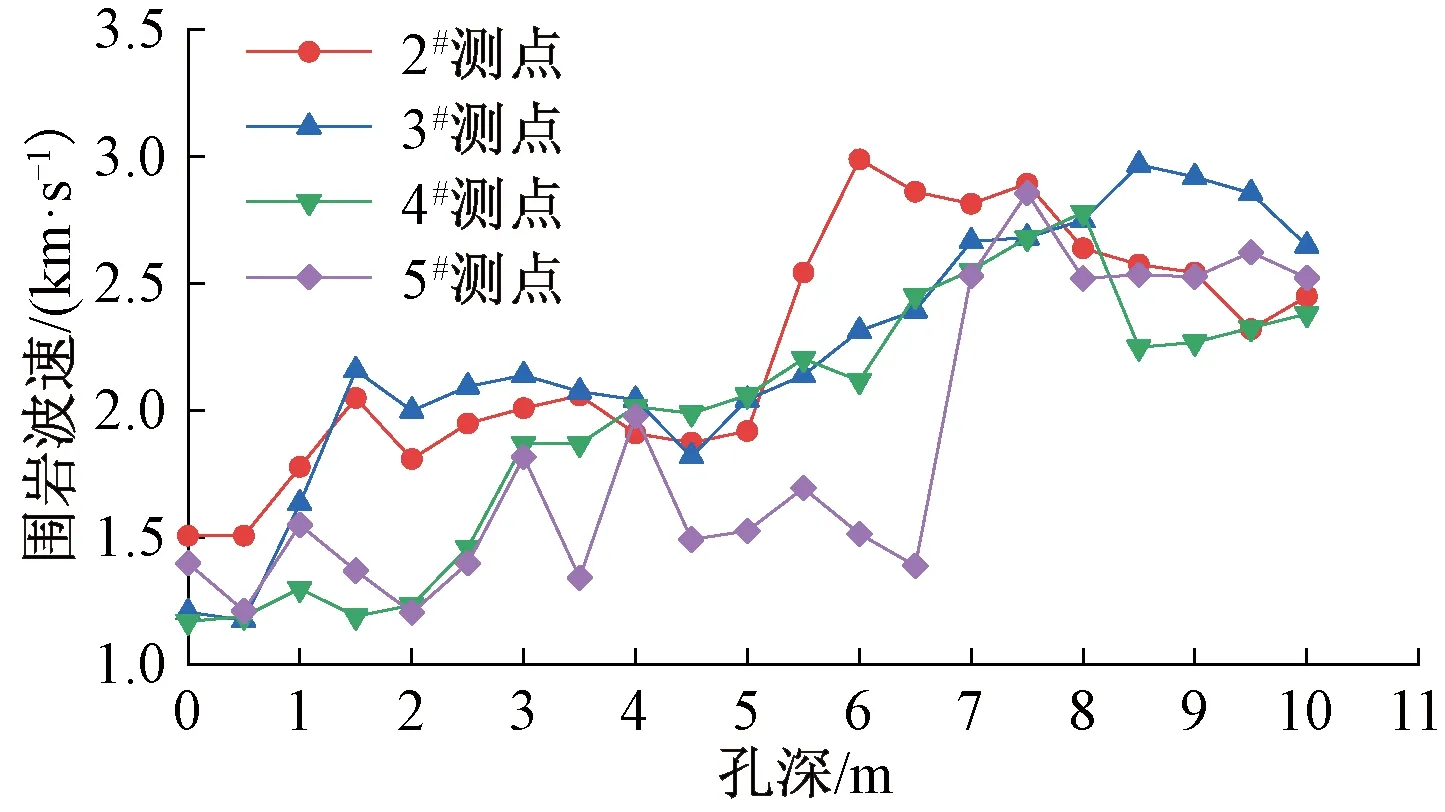
圖5 嚴重大變形段圍巖波速隨深刻變化規律

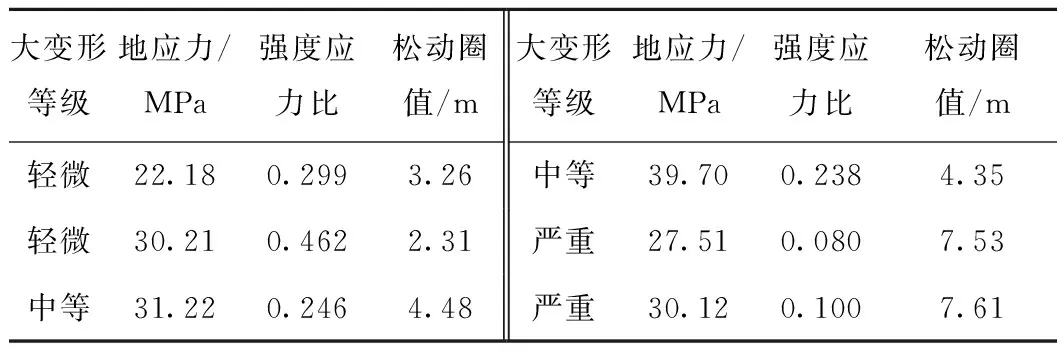
表2 圍巖松動圈測試結果

結合不同等級大變形隧道圍巖松動圈范圍，錨桿長度見表3[42]。

基于圍巖松動圈測試結果，建立圍巖強度應力比與松動圈厚度的擬合式為

LP=-3.244lnNc-0.315

(1)

式中：LP為圍巖松動圈厚度，m；Nc為巖體強度應變比。

表3 軟巖大變形隧道松動圈值及錨桿長度

全長黏結錨桿承載力計算式[47]為

(2)

式中：Sa、Sb為錨桿縱向、環向間距；ψ為錨固長度對黏結強度的影響系數；Pa,b為錨桿支護抗力；D為錨桿鉆孔直徑，取50 mm；L為錨桿錨固長度，取錨桿長度的一半；fmg為黏結材料與圍巖黏結強度，軟巖地層取0.3～0.8。

假定錨桿提供的支護力與初始地應力之比為0.04，考慮錨桿縱向間距與鋼拱架的關系，參考相關工程經驗，縱向間距取1.2 m，則錨桿環向間距計算結果見表4。

則軟巖隧道錨桿支護參數見表5。

表5 錨桿參數優化

對于嚴重及極嚴重大變形段，采用長短組合錨桿進行支護。長短錨桿對大變形控制作用分別從力學機制和施工工藝兩方面進行分析。首先隧道開挖后圍巖為漸進式破壞，松動圈隨開挖和時間逐漸增大，施作短而密的錨桿，可有效提高圍巖力學性質，形成承載拱，發揮圍巖的承載能力。隨著松動圈的進一步發展，短錨桿隨塑性區整體向內移動，長錨桿施作后將承載拱與深部圍巖形成整體，使圍巖應力向深部轉移，從而有效降低結構荷載。其次，由于隧道圍巖穩定性極差，多采用三臺階法(預留核心土)進行施工，施工空間嚴重制約了長錨桿的施作，使錨桿施作時機滯后，上臺階錨桿在中臺階開挖后進行施作，不能及時發揮錨桿錨固作用。長短組合錨桿指隧道拱部先進行短錨桿施作，待中臺階開挖完成后一次性完成中上臺階長錨桿施作。短錨桿可以及時施作，對淺層圍巖進行及時加固，與拱架共同作用，提供的支護反力可以減少即時松動圈內剪脹變形，同時使淺層圍巖形成壓縮拱，改善結構受力，控制圍巖變形[48-50]。

短錨桿應達到圍巖瞬時松動圈厚度，長錨桿達到穩定松動圈厚度，其中瞬時松動圈按60%穩定松動圈厚度確定[5]。

3.2.3 長短組合支護效果

為進一步明確長短組合錨桿在軟巖隧道中的變形控制作用，在茂縣隧道1#斜井(嚴重大變形段)開展了等長錨桿、長短組合錨桿對比試驗，其中長短組合錨桿布置示意見圖6[46,51]。XJ1K0+232～220為等長的8 m錨桿試驗段，記為A1試驗段；XJ1K0+220～208為長短組合錨桿試驗段，長錨桿為8 m，短錨桿為3 m，記為A2試驗段。試驗段長錨桿軸力分布見圖7。

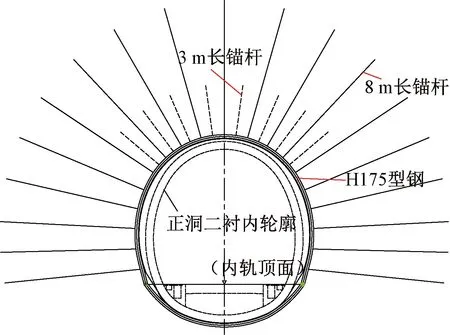
圖6 長短組合錨桿布置示意

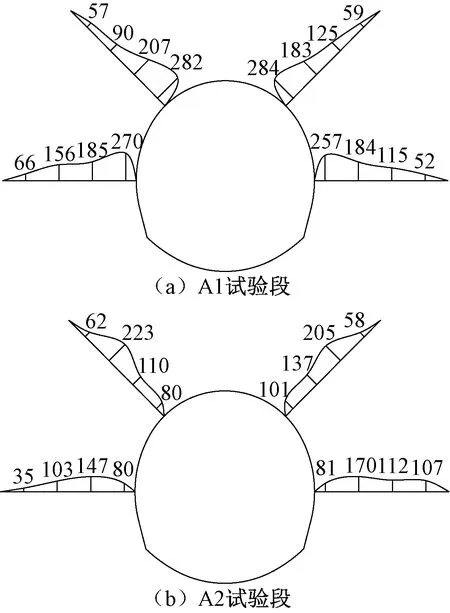
圖7 錨桿對比試驗段錨桿受力包絡圖(單位：kN)

由圖7可知，等長錨桿與長短組合錨桿試驗段長錨桿軸力分布明顯不同，等長錨桿軸力隨著圍巖深度增加逐漸減小，而長短組合錨桿軸力呈現中間大，兩頭小的分布。其主要原因是軟巖大變形隧道中淺層圍巖破壞非常嚴重，變形量大，使錨桿軸力非常大，同時，臺階施工時在拱架下沉作用下，一定的剪應力使軸力增長。而長短組合錨桿由于短錨桿形成的淺層壓縮拱使淺層圍巖變形相對較小，降低了長錨桿淺層段剪應力，長錨桿為使淺層壓縮拱與深層圍巖協調變形，中性點向深部圍巖轉移。

兩組試驗典型斷面隧道變形時程曲線見圖8。圖8中，A為拱頂下沉，S1、S2為邊墻收斂。

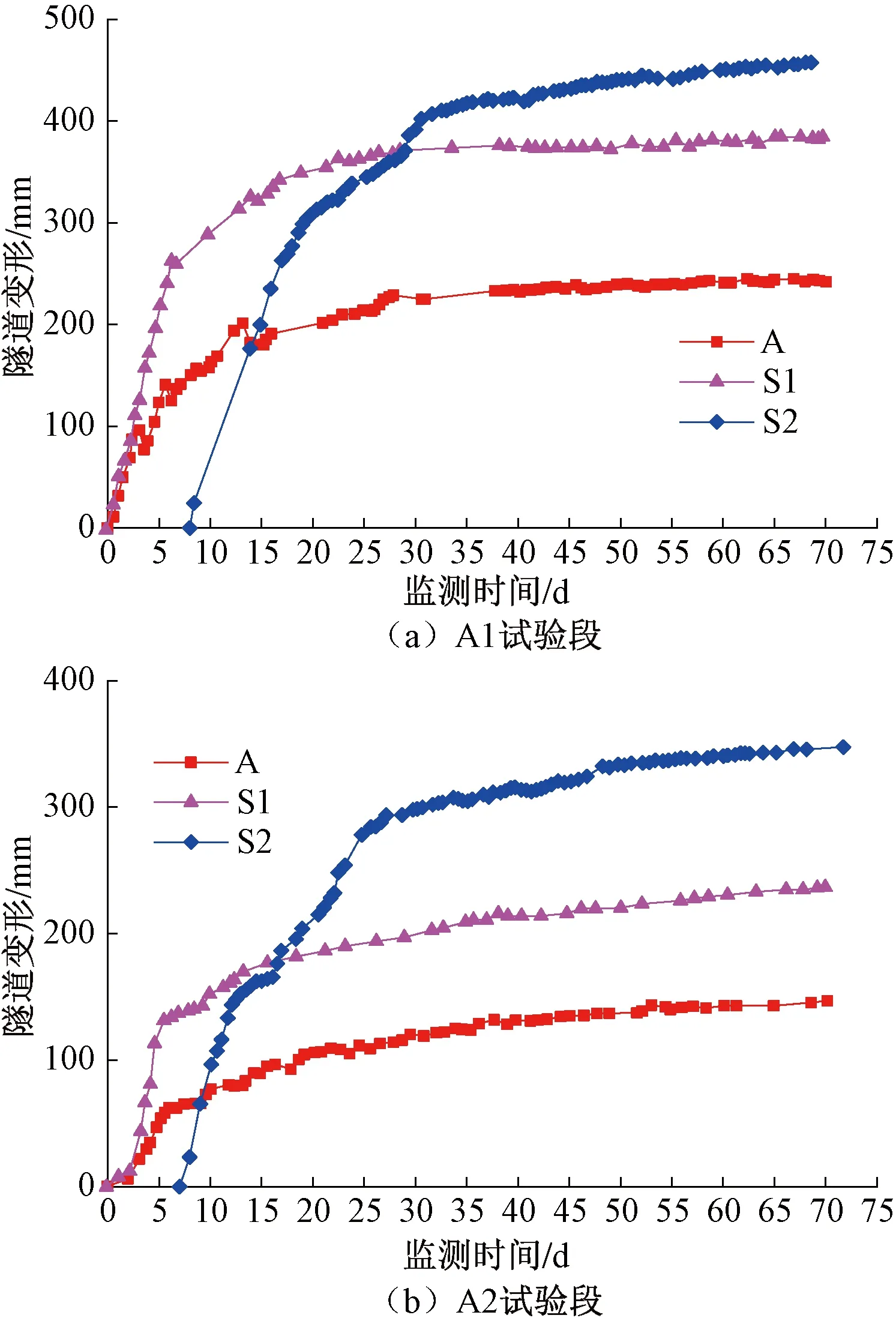
圖8 試驗段變形時程曲線

由圖8可知，從變形發展過程來看，上臺階施工完成后兩試驗段變形量基本相當，但由于A2試驗段采用了長短組合錨桿支護，隧道變形速率及最終變形量明顯小于A1試驗段，可使拱頂下沉減少30%左右。說明短錨桿隨著施工推進，逐漸發揮對變形的控制作用，但其控制效果需隨開挖過程逐漸體現。

3.3 開挖方法優化

目前對于軟巖大變形隧道開挖方法，多采用三臺階分部開挖，但三臺階開挖方法初支封閉距離長，對圍巖形成多次擾動，施工空間小，不利于長錨桿施工。同時由于軟巖隧道變形量大，變形速率高，三臺階開挖成洞性差，如臺階連接處由于隧道變形造成鋼拱架連接不密貼，噴射混凝土不密實等，造成結構受力薄弱，進一步加劇邊墻變形。

為明確二臺階帶拱仰開挖方法的變形控制效果，選取楊家坪隧道DK117+420—DK117+480作為試驗段(中等大變形段)，分別進行三臺階開挖方法和二臺階帶仰拱開挖方法試驗。分別對隧道變形、接觸壓力、拱架應力及錨桿軸力進行監測，測點布置見圖9。

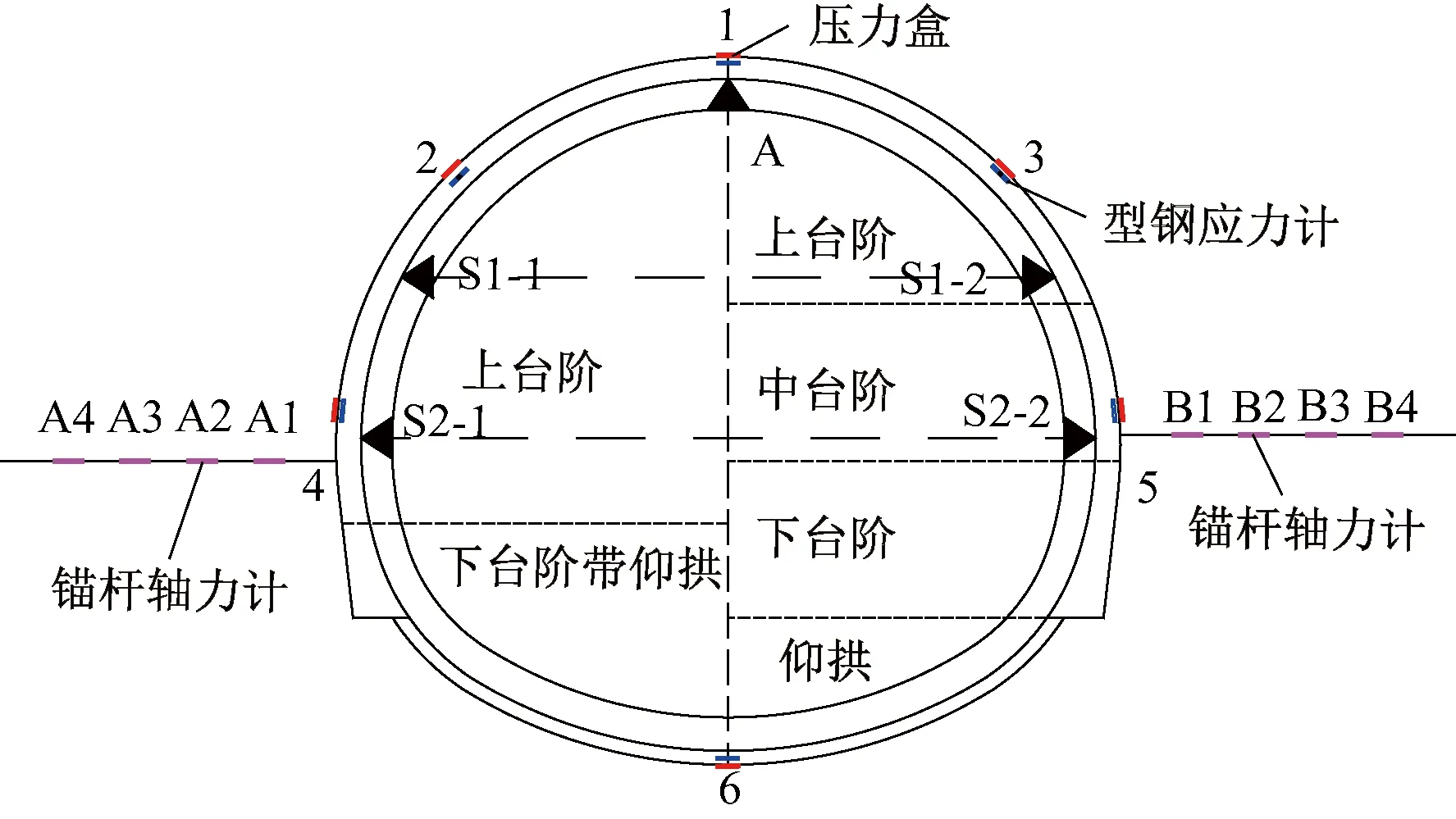
圖9 測點布置

3.3.1 隧道變形

兩種開挖方法下典型圍巖變形時程曲線見圖10。由圖10可知，隧道變形受施工過程影響顯著，變形呈臺階式增長，尤其當采用三臺階開挖時，中下臺階開挖時隧道變形速率明顯增大。同時比較兩種開挖方法的隧道變形過程，二臺階帶仰拱開挖方法的變形收斂時間和變形量明顯小于三臺階開挖方法。

3.3.2 圍巖壓力

初支與圍巖接觸壓力時程曲線見圖11。

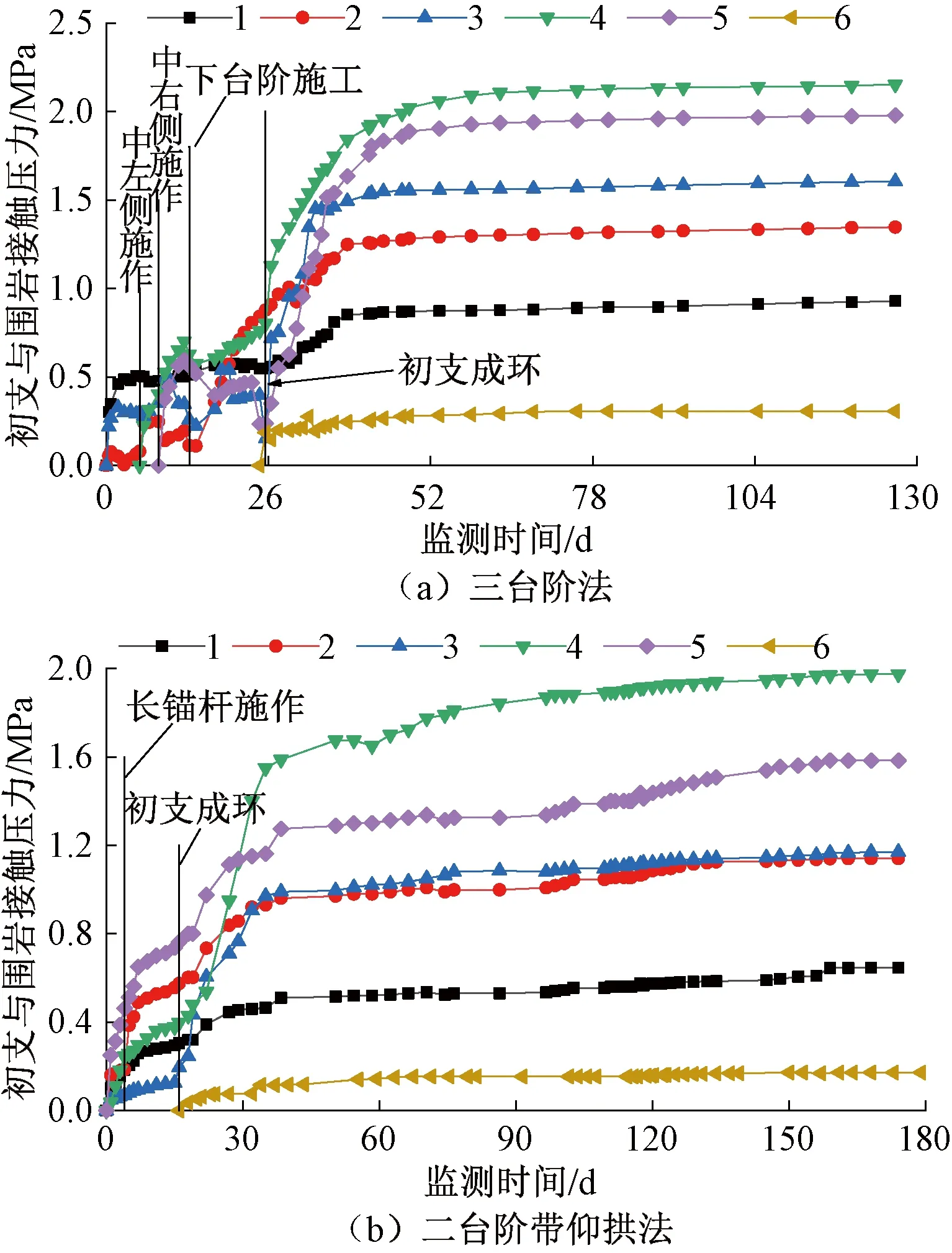
圖11 初支與圍巖接觸壓力時程曲線

由圖11可知，圍巖接觸壓力受臺階開挖影響更加明顯，三臺階開挖時尤其明顯，受擾動影響，中下臺階開挖時圍巖接觸壓力會出現減小現象，而二臺階帶仰拱開挖方法下，圍巖接觸壓力持續增長，當長錨桿施作后增長速率明顯減小。雖然二臺階帶拱仰開挖方法的圍巖接觸壓力在前期較大，但由于長錨桿的及時施作，當初支封閉成環時兩種開挖方法的圍巖接觸壓力基本相當，但后期三臺階開挖方法的圍巖接觸壓力仍保持較大速率的增長，造成最終圍巖接觸壓力較大。

上述分析說明，二臺階帶仰拱開挖方法對圍巖的擾動較小，結構整體性更好，雖然由于變形釋放較小，造成前期圍巖接觸壓力較大，但由于長錨桿的及時施作，充分發揮了長錨桿對圍巖的支護作用，最終圍巖接觸壓力較小，初支與圍巖接觸壓力包絡圖見圖12。圖12中，括號內外數值分別為兩臺階帶仰拱法和三臺階法開挖時初支與圍巖接觸壓力值。

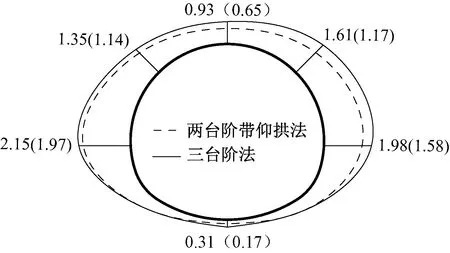
圖12 初支與圍巖接觸壓力包絡圖(單位：MPa)

3.3.3 鋼架應力

型鋼拱架應力時程曲線見圖13。由圖13可知，拱架承受壓應力。三臺階開挖時，拱架應力增長波動明顯，尤其是當中臺階開挖時拱肩部位應力變化明顯。二臺階帶仰拱方法開挖時，拱架應力隨開挖進程持續增長，但長錨桿施工完成后邊墻部位拱架應力增長速率明顯減小。從最終結果來看，二臺階帶仰拱法可以減小拱架上部應力，增大邊墻及仰拱應力，充分利用拱架承載力，控制邊墻位移。

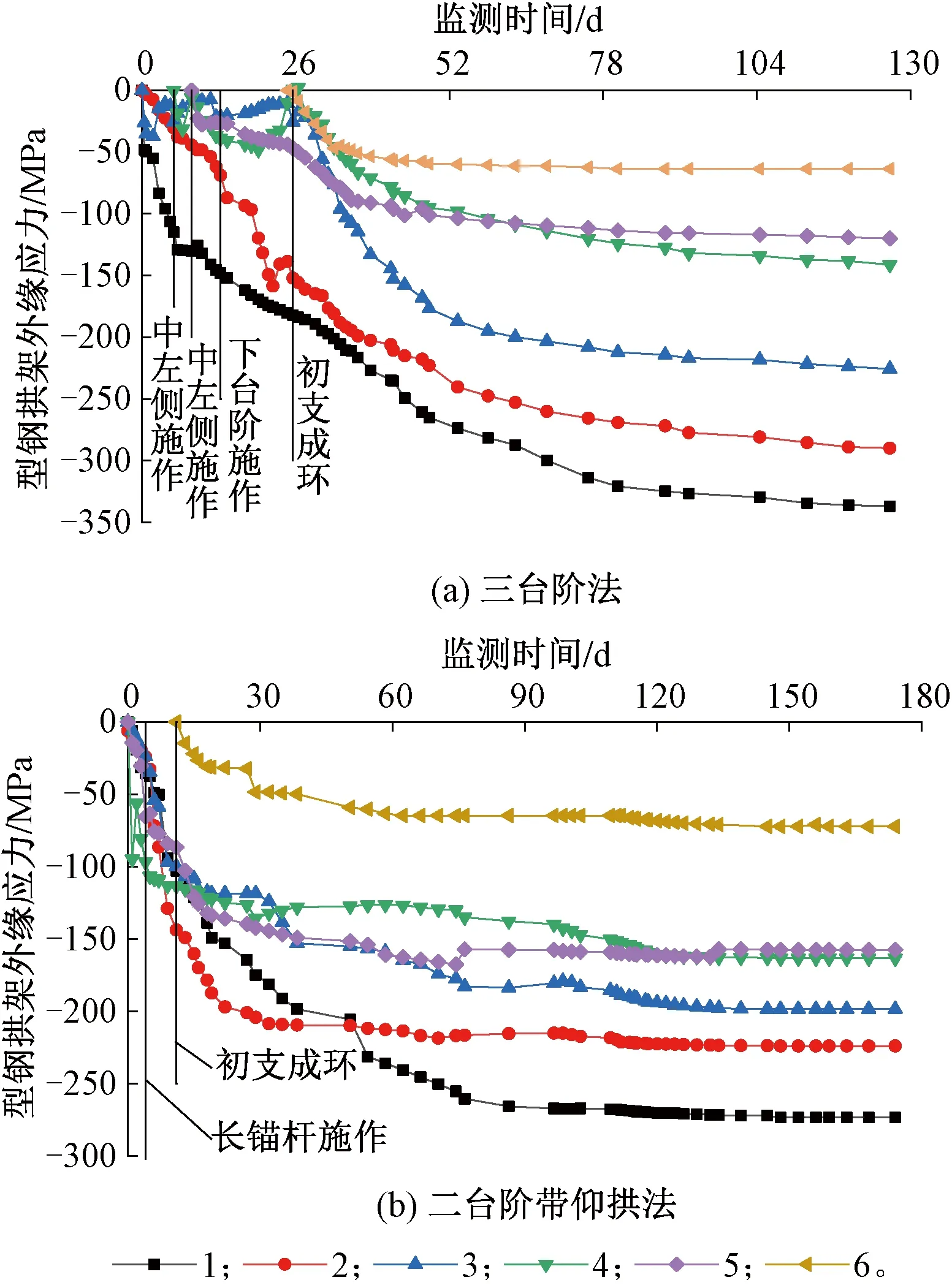
圖13 初支型鋼拱架應力時程曲線

3.3.4 錨桿軸力

邊墻錨桿軸力時程曲線見圖14。

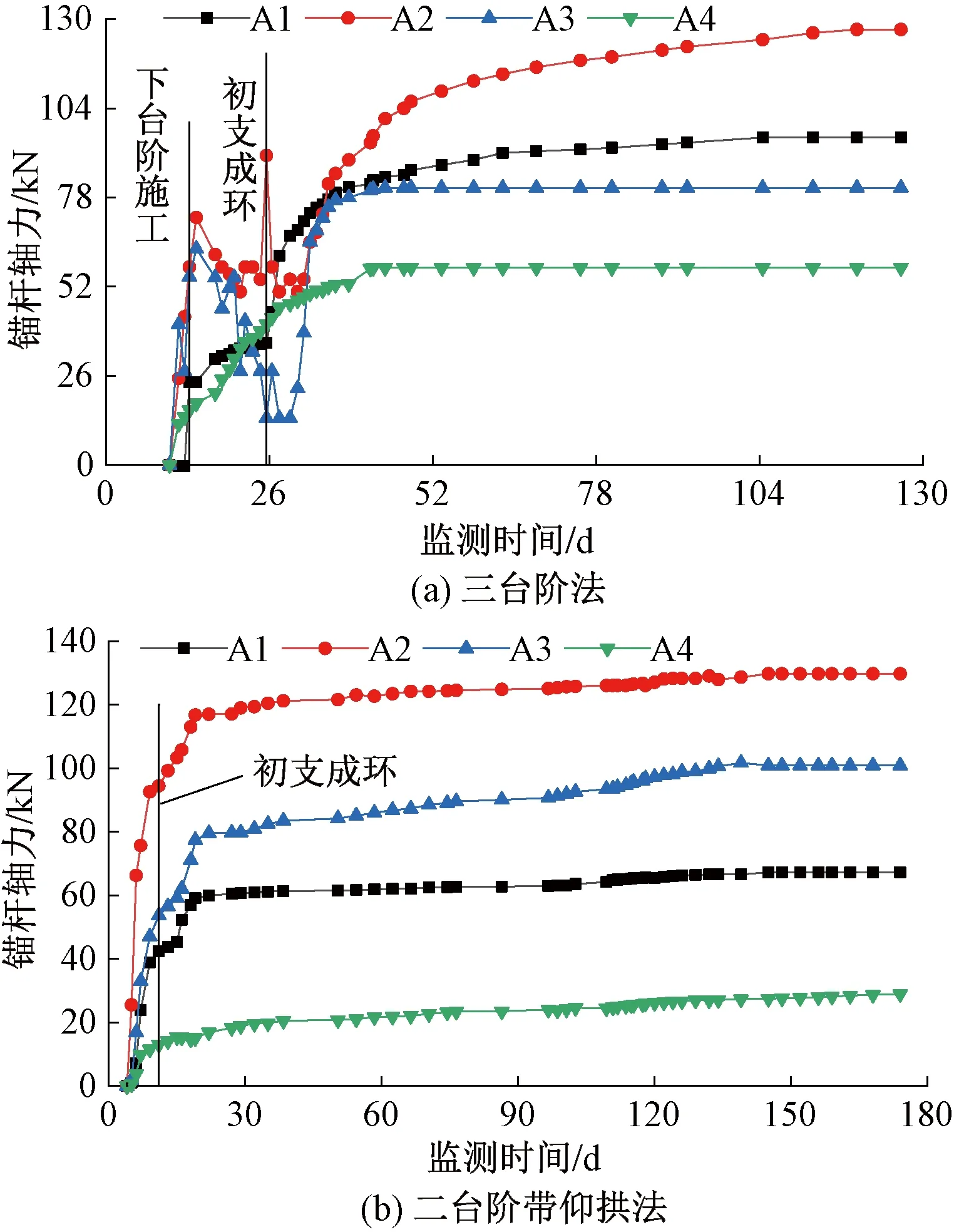
圖14 錨桿軸力時程曲線

三臺階開挖方法下錨桿軸力在施作后快速增長，但在下臺階、仰拱開挖時出現明顯減小，說明臺階開挖擾動的作用阻礙了錨桿控制作用的發揮。而二臺階帶拱仰開挖時，錨桿施作后軸力持續增長，受后續施工影響較小。同時比較兩種開挖方法，初支封閉時錨桿軸力，二臺階帶仰拱開挖方法明顯大于三臺階開挖方法，說明錨桿發揮了更大的控制作用。這也是雖然二臺階帶仰拱法應力釋放較小但是結構受力較小的重要原因。

3.4 二次襯砌施作時機[52]

二襯結構安全性是軟巖隧道面臨的重要難題，而二次襯砌施作時機對結構安全性具有重要影響，同時也是反映軟巖隧道主動支護理念的重要方面。

由于軟巖具有顯著的流變特性，其流變荷載具有明顯的時間效應，考慮隧道施工過程，大部分流變荷載將由二襯承擔。雖然在大變形隧道實踐過程中也不乏通過提前施作大剛度二襯控制圍巖變形的成功案例，但這與大變形等級、巖體擠壓程度相關。同時大剛度二襯控制圍巖變形與抗放結合的主動控制理論不符，科學性及經濟性較差。

基于茂縣隧道1#斜井未施作二襯的隧道變形長期監測結果見圖15，目前的變形主動控制手段可以使圍巖變形達到階段性穩定，但如果長時間未施作二次襯砌，柔性初期支護會由于流變荷載發生承載力下降，變形加劇現象。結合主動控制的大變形控制理念，認為二襯可以在初期支護達到第一穩定階段后施作，這樣既可以通過有效控制的位移釋放，減小二襯受力，同時又可以利用二襯的大剛度控制圍巖流變。

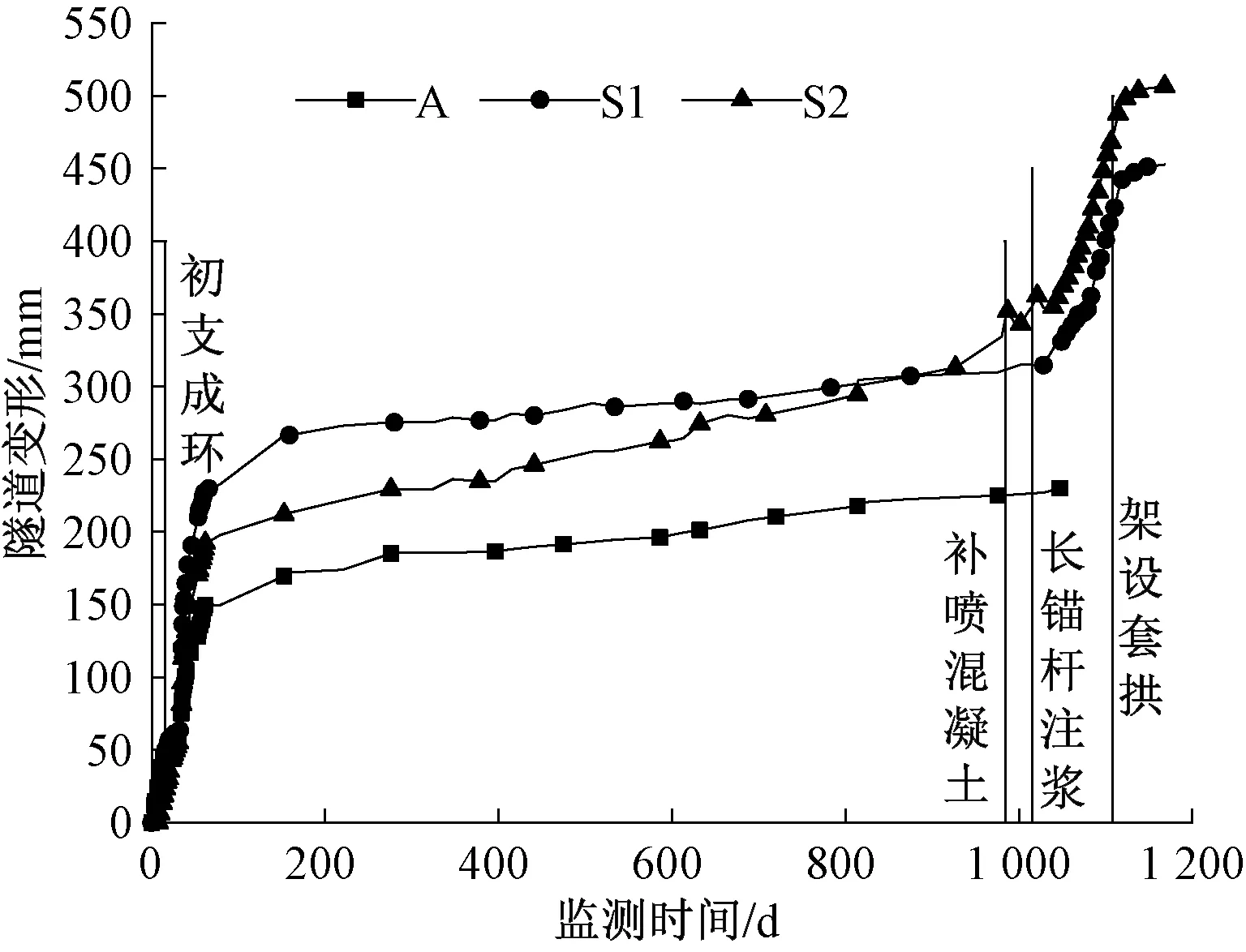
圖15 茂縣隧道1#斜井變形時程曲線

基于實測變形數據統計，以初期支護變形達到第一穩定階段變形量95%對應的變形速率作為二次襯砌施作變形速率標準，以不同大變形等級統計結果的80%保證率確定二次襯砌施作時機。對達到二次施作速率標準的時間進行統計，確定不同大變形等級下隧道二襯施作時間，進一步方便現場實際應用，隧道變形穩定時間(ti)正態分布曲線見圖16。最終成蘭鐵路軟巖隧道二次襯砌施作標準見表6。

圖16 隧道變形穩定時間正態分布曲線

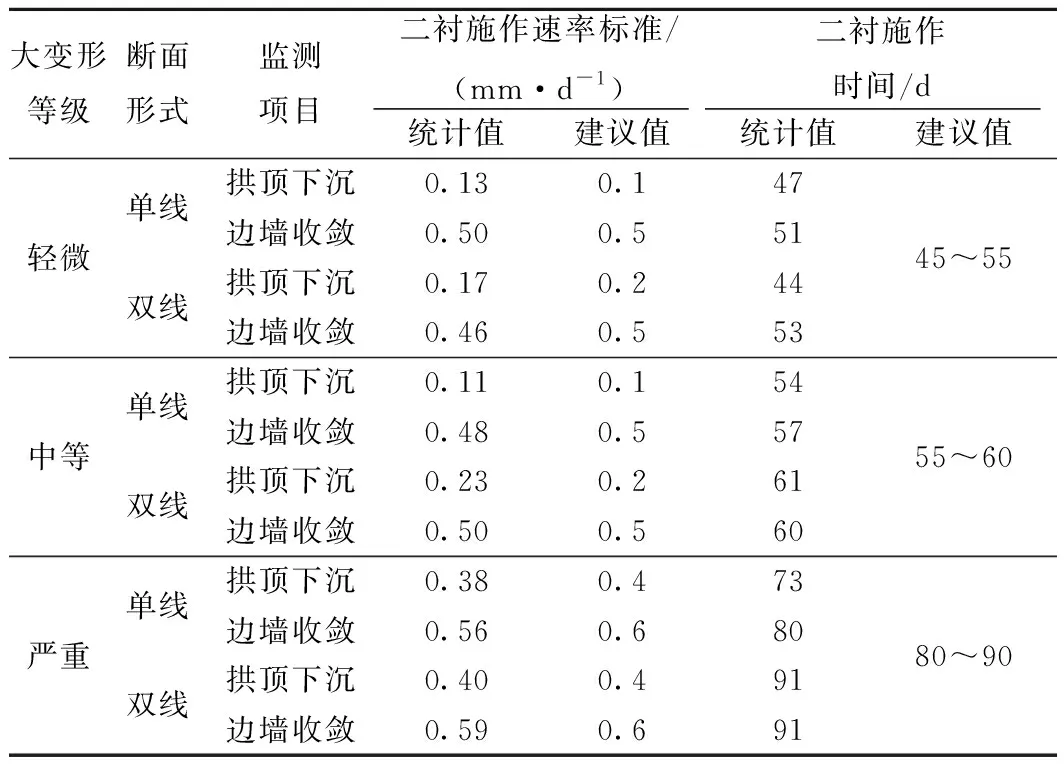
表6 成蘭鐵路軟巖隧道二襯施作標準

3.5 型鋼拱架

目前國內隧道拱架多采用格柵拱架和型鋼拱架，其中格柵拱架與混凝土黏結性好，具有較好的受力性能，型鋼拱架剛度大，支護力強。為探明不同拱架類型的作用效果，在茂縣隧道1#斜井的嚴重大變形段開展了格柵I20b、I20b+I20b、H175三種類型拱架的現場試驗，其變形時程曲線見圖17[46,51]。

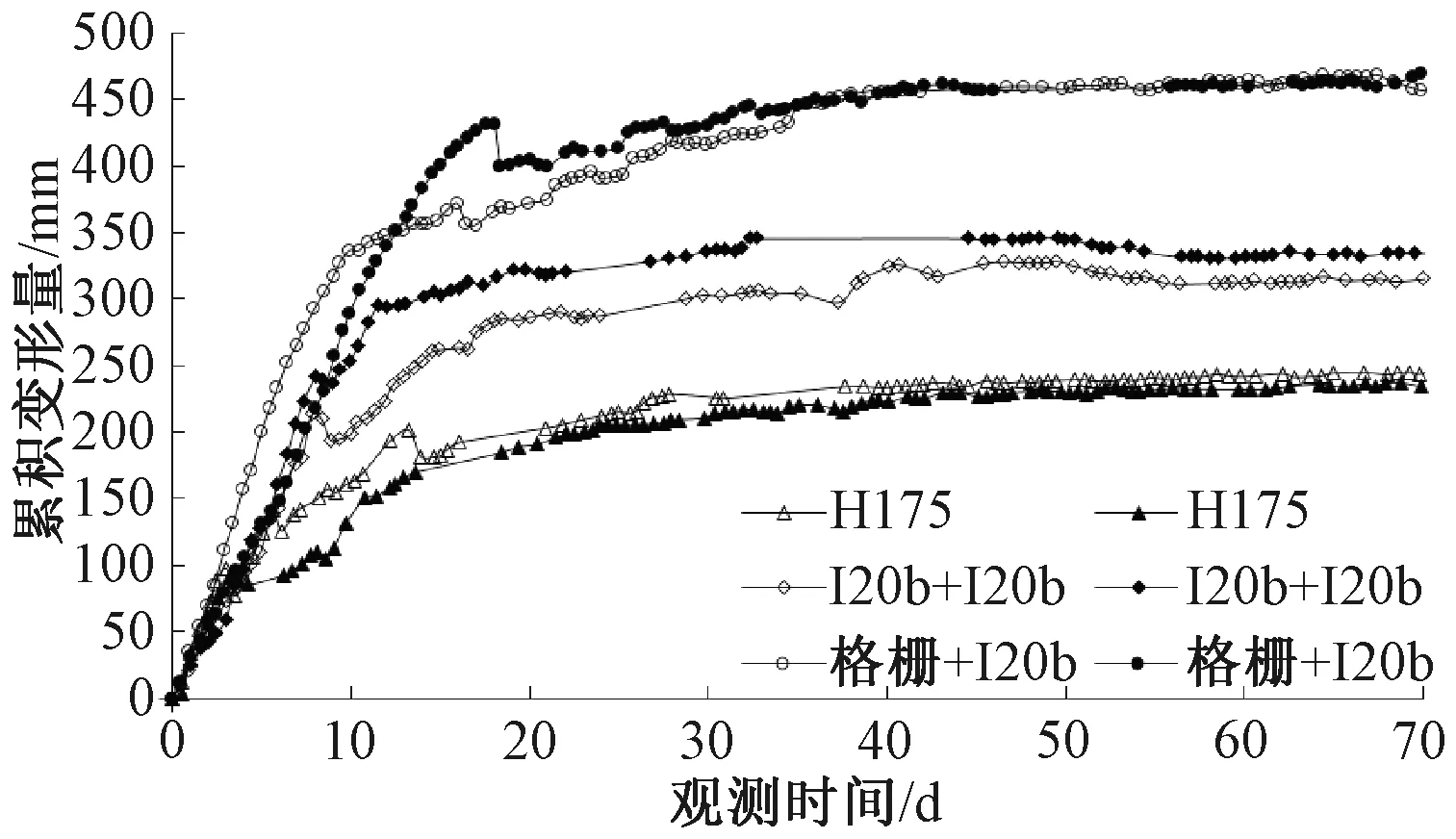
圖17 不同類型拱架變形時程曲線

由于H175型鋼拱架剛度大，從變形速率和變形量來看，明顯優于其他兩種類型的拱架。由此可知，增大支護剛度，可以有效控制圍巖變形。但支護剛度增大，初期支護所受荷載明顯增大，因此，針對不同大變形等級，應逐步提高初期支護中拱架的剛度，既可以有效控制圍巖變形，又可以適當進行荷載釋放。

同時，隨著大變形等級的逐漸提高，型鋼拱架破壞不僅表現為橫斷面的彎折，而且表現為縱向的失穩，因此，為加強拱架的整體性，采用工字鋼加強拱架的縱向連接。

3.6 工藝優化

現場試驗過程中，針對大變形特點，提出如下施工工藝優化：

(1)優化超前支護布置

超前支護是保持掌子面穩定，保證施工安全的重要手段。軟巖隧道不僅拱部圍巖穩定性差，而且邊墻也常出現圍巖剝落、掉塊等情況。因此，將目前常用的拱部120°超前支護擴大為180°。

(2)鎖腳錨桿布置優化

鎖腳錨桿布置以徑向方式施作，并在邊墻鋼架分布式施作，對保證鋼架的整體穩定，防止鋼架局部失穩起到了較好效果，鎖腳錨桿優化見圖18。

圖18 鎖腳錨桿優化

(3)錨桿墊板優化

隨著錨桿加長，開挖工法優化，錨桿所受軸力不斷增大，現場出現了錨桿與墊板、螺帽不匹配問題，錨桿破壞以螺帽拉脫，墊板凹陷為主。因此現場采用加大加厚的錨桿墊板，墊板邊長為20 cm，厚度為1 cm。

3.7 施工機械配套

前期我國隧道機械化配套施工的目的主要集中于提高施工進度，改善作業環境等，隨著施工技術的不斷提高，圍巖變形機制研究不斷深入，機械化施工不僅關系著施工進度、施工質量，而且對施工安全、變形控制效果更具有顯著的影響。尤其對于軟巖大變形隧道，必須主動支護圍巖，在減少對圍巖擾動的同時，主動改善圍巖的應力狀態是關鍵，因此，大斷面開挖，長錨桿施作，及時支護是必然選擇。而上述技術措施的實現，必然需要機械化配套施工[53-54]。

施工機械除常規的挖掘機、裝載車、出碴車外，主要涉及到錨桿鉆機、混凝土噴射機及拱架臺車[43]。

在鉆爆階段，由于炮眼深度淺，數量大，可采用手持風鉆進行施工，以數量換速度。但由于軟巖隧道系統錨桿長度大，手持風鉆工效低，拱部長錨桿施作角度限制大。同時由于進口錨桿鉆機價格昂貴，為此課題組聯合廠家研發了針對軟巖隧道的錨桿專用鉆機，不僅可實現360°全環施工，而且雙臂同時施工，工作效率高，現場應用表明8 m長自進式錨桿的施作時間可控制在20 min以內。

軟巖大變形隧道多采用大剛度型鋼拱架，如I20b、HW175甚至H200型鋼。隨著型鋼型號提高，拱架單位質量逐漸增大，不僅造成工人勞動強度大，而且單榀架設時間長。尤其采用上述大斷面開挖方法時，雙線隧道上臺階HW175型鋼拱架的重量達10 kN以上，采用人工架設時難度極大。為此引進三臂拱架臺車，增加拱架架設效率的同時，將上臺階拱架由5節改為3節，既減少受力薄弱環節又可以節省時間。

3.8 動態調整

雖然上述分析針對大變形等級提出了針對性措施，但由于地質條件的變異性，勘測技術的局限性，大變形分級預測技術的不完善性[1,55]，在隧道勘察階段及施工階段，面對復雜多變的地質條件，很難快速、準確的判斷大變形等級，進而采用針對性措施。

因此，成蘭鐵路針對軟巖大變形隧道采用動態設計的理念，在勘察及施工前期大量實測資料的基礎上，對大變形等級進行初步判定。在此基礎上，結合施工過程中圍巖揭露情況，埋深，已施工段結構變形及受力情況以及必要的試驗測試數據，采用“多方會診”，對大變形等級進行確認及短距離預測，及時調整施工方案，實現動態調整。

3.9 成蘭鐵路軟巖隧道變形控制體系

基于上述研究，并參考一定的工程經驗，成蘭鐵路軟巖隧道變形控制體系見表7[42]。

表7 成蘭鐵路軟巖隧道變形控制體系

4 基于施工過程的隧道變形特征

4.1 變形數據統計

基于上述變形控制技術，分別對大變形等級條件下單、雙線隧道變形進行分類統計，變形監測項目分別為拱頂下沉A、邊墻收斂S1和S2，其中S1-1、S1-2、S2-1和S2-2分別為S1和S2的位移監測點。由于斷面型式、開挖方法較多，以雙線隧道為例，S1位于拱肩，S2位于邊墻，見圖19。

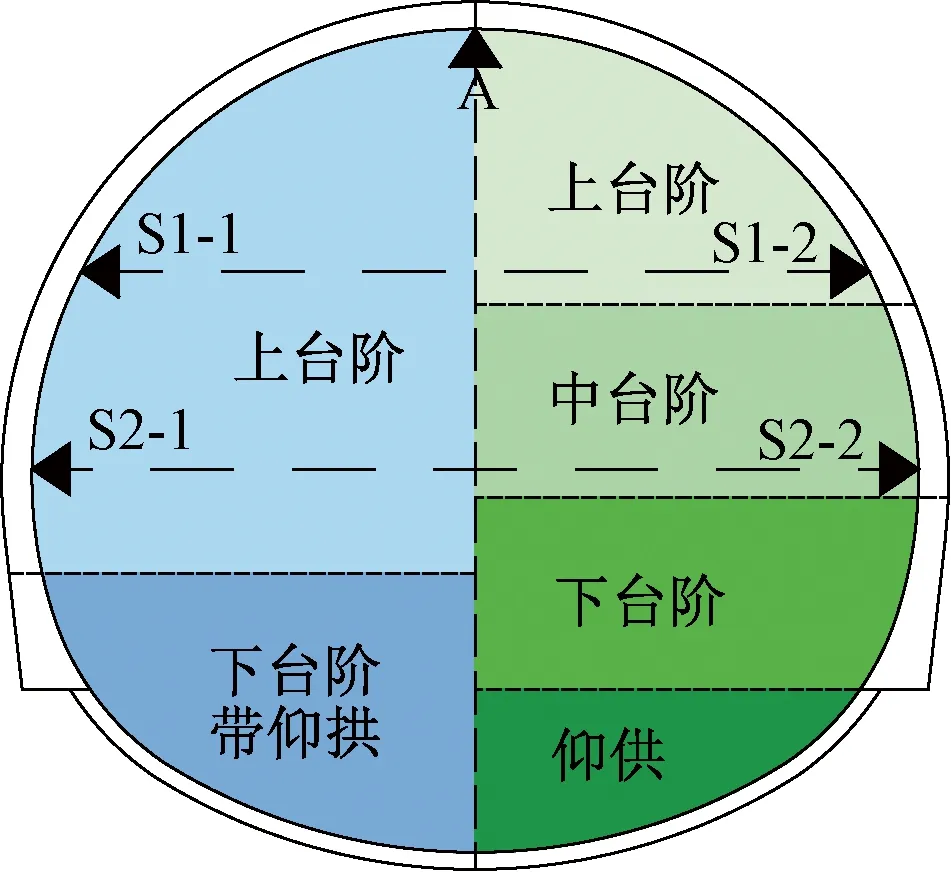
圖19 隧道變形量測點布置示意

單線鐵路隧道輕微、中等、嚴重大變形段監測斷面分別為153、96、68個，雙線鐵路隧道輕微、中等、嚴重大變形段監測斷面分別為101、199、35個。極嚴重大變形段缺少統計樣本。部分隧道變形分布見圖20。

由圖20可知，雖然對隧道變形進行了分類統計，但由于地質條件及施工條件的復雜性，隧道變形量具有較大的離散性，而且隨著變形等級提高，離散性變大。如輕微大變形段邊墻位移最小值為46.6 mm，最大值276.9 mm，相差約5.9倍；嚴重大變形段邊墻位移最小值為66.2 mm，最大值為561.99 mm，相差近8.5倍。這主要是由于軟巖隧道變形影響因素眾多，大變形等級越高，地質條件、隧道支護措施及施工過程越復雜，導致隧道變形離散性越大。

4.2 隧道變形特征分析

4.2.1 典型變形時程曲線

典型斷面隧道變形時程曲線見圖21。由圖21可知，三種大變形等級下隧道變形與時間密切相關，按隧道變形速率可分為快速增長階段、持續增長階段和緩慢增長階段，并且大變形等級越高，快速增長階段變形速率越大，變形振蕩增長越明顯，變形持續時間越長。同時隧道變形時程規律受開挖方法影響，邊墻位移尤其明顯，中下臺階開挖時，邊墻位移速率明顯增大，變形呈臺階式增長。

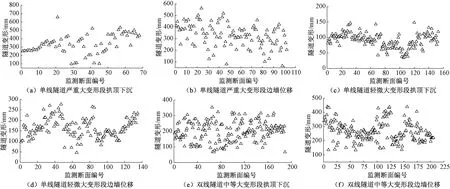
圖20 單、雙線隧道變形分布

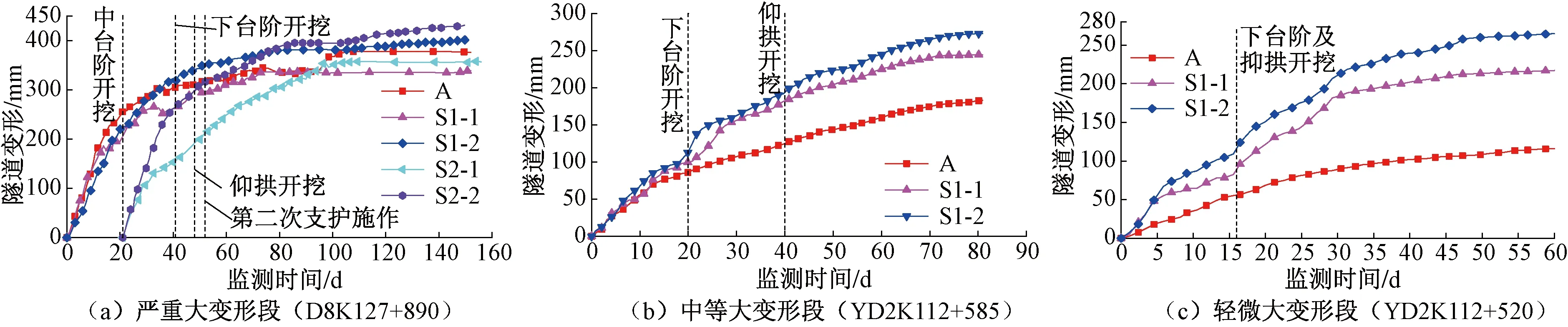
圖21 典型斷面變形時程曲線

4.2.2 各施工階段隧道變形占比分析

結合施工過程，對各施工階段隧道變形量與總變量的比值(變形占比)進行統計，其中單線隧道嚴重大變形段統計結果見圖22。

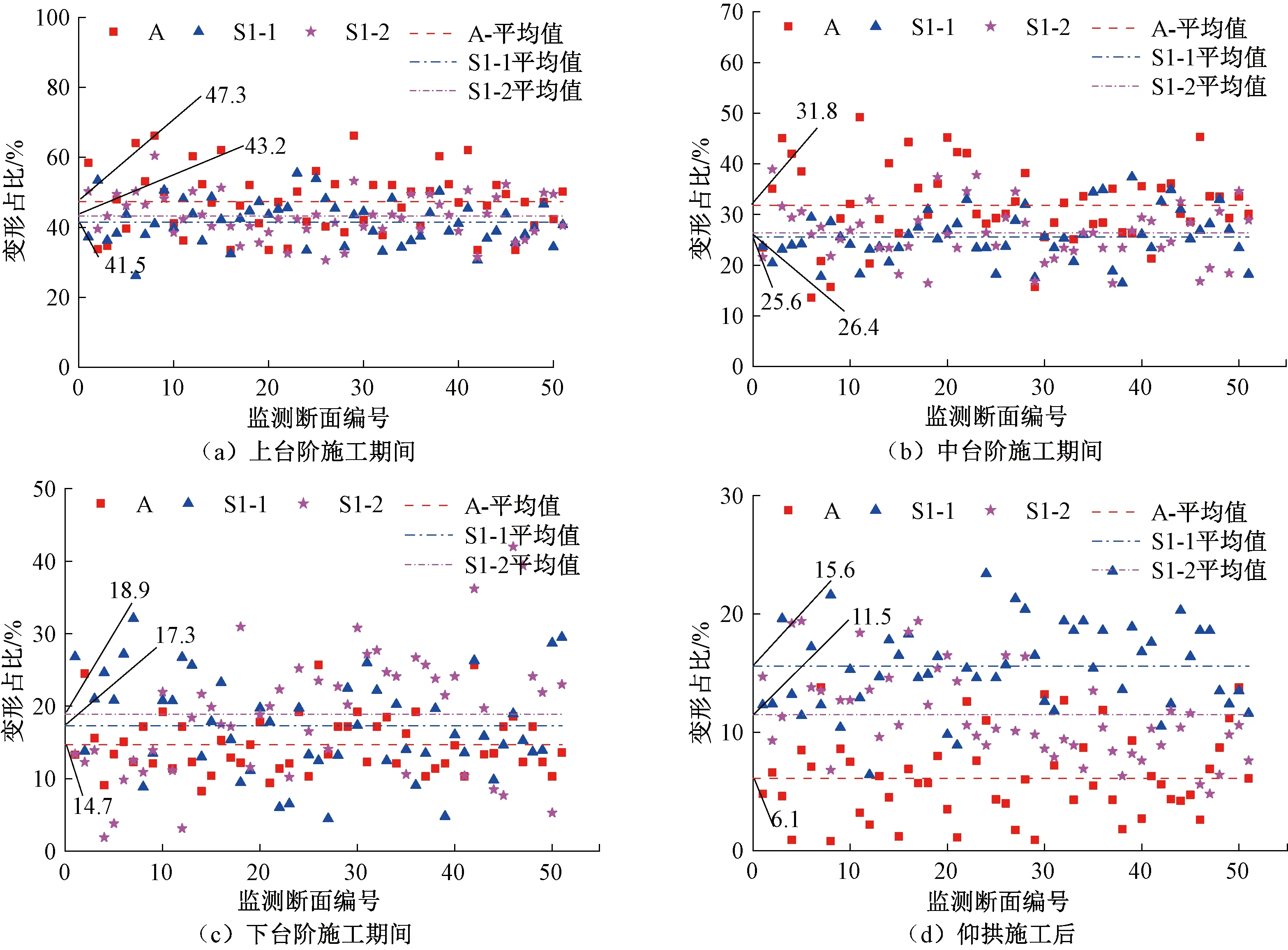
圖22 單線隧道嚴重大變形占比分布

由圖22可知，嚴重大變形段各施工階段隧道變形占比相對集中于某一區域內。隧道變形主要發生在上臺階施工期間，變形占比達到41.5%～47.3%，中、下臺階及仰拱施工期間變形占比逐漸減小。并且拱頂下沉在中、上臺階施工期間變形占比明顯高于邊墻位移，仰拱施工后變形占比低于邊墻位移變形占比，因此，在隧道施工期間，前期應重點關注拱頂下沉變形，后期應加強邊墻位移控制。最終不同大變形等級下隧道各施工階段變形占比平均值分布見圖23。

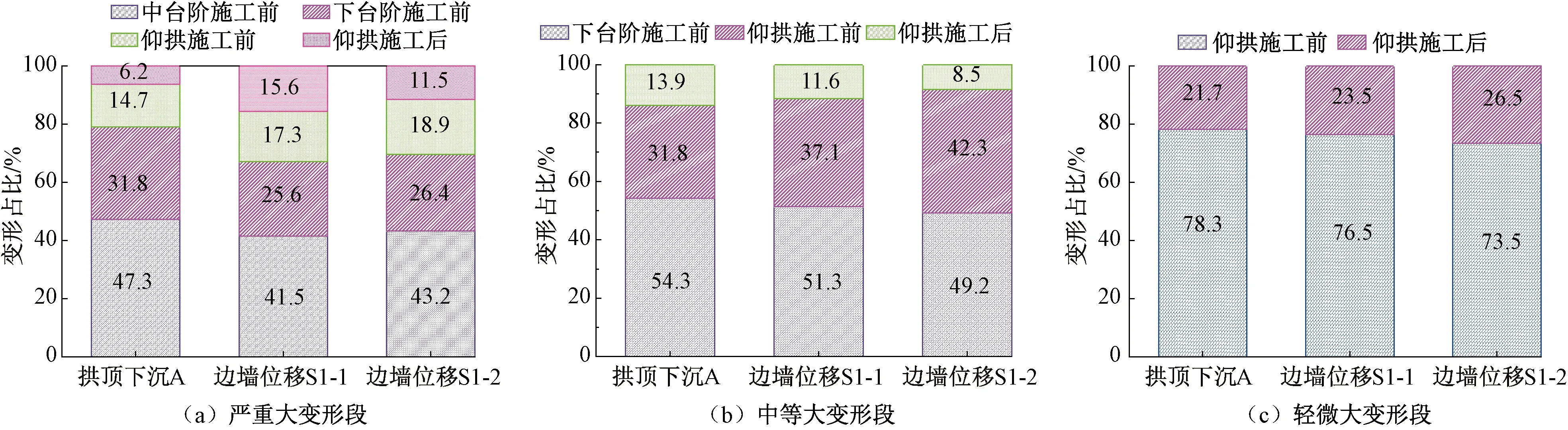
圖23 隧道變形時空效應分布圖

通過嚴重大變形段與中等大變形段隧道變形時空效應分布可知，隨著大變形等級提高，隧道變形在上臺階施工期間變形占比減小，仰拱施工后變形占比增大，說明隨著大變形等級提高，圍巖流變性增強，隧道變形的時間效應更加明顯。同時隧道變形的時空效應受開挖方法影響明顯，輕微大變形段采用二臺階帶仰拱開挖方法，開挖分步少，初支封閉時間短，變形釋放更小，仰拱施工后變形占比更大。

同時比較發現，拱頂下沉與邊墻位移的時空效應差別較大，邊墻位移在仰拱施工后變形占比更大，時間效應更加明顯，對變形控制不利，而隧道以邊墻位移為主，因此以邊墻位移為準，各施工階段變形占比見表8。

表8 各施工階段隧道變形占比

5 隧道變形控制基準

5.1 隧道變形量統計規律

雖然隧道變形量受各種因素影響具有一定離散性，但某一大變形等級下隧道變形相對集中于一定范圍內，其分布服從統計學中的正態分布規律[56]。因此本文采用數理統計學方法對隧道變形數據進行處理，進而確定隧道預留變形量。

當分布函數中方差σ2未知時，由于樣本方差S2是總體分布方差σ2的無偏估計，則

(3)

則隧道變形量平均值的置信水平為(1-α)的一個置信區間為

(4)

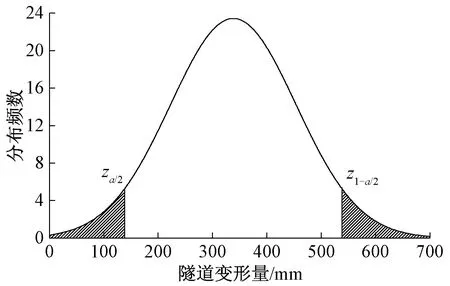
圖24 隧道變形量區間估計示意

對上述隧道變形量統計樣本進行分布規律顯著性檢驗，并進行分布函數擬合，隧道變形量分布頻數直方圖及擬合函數見圖25、圖26。

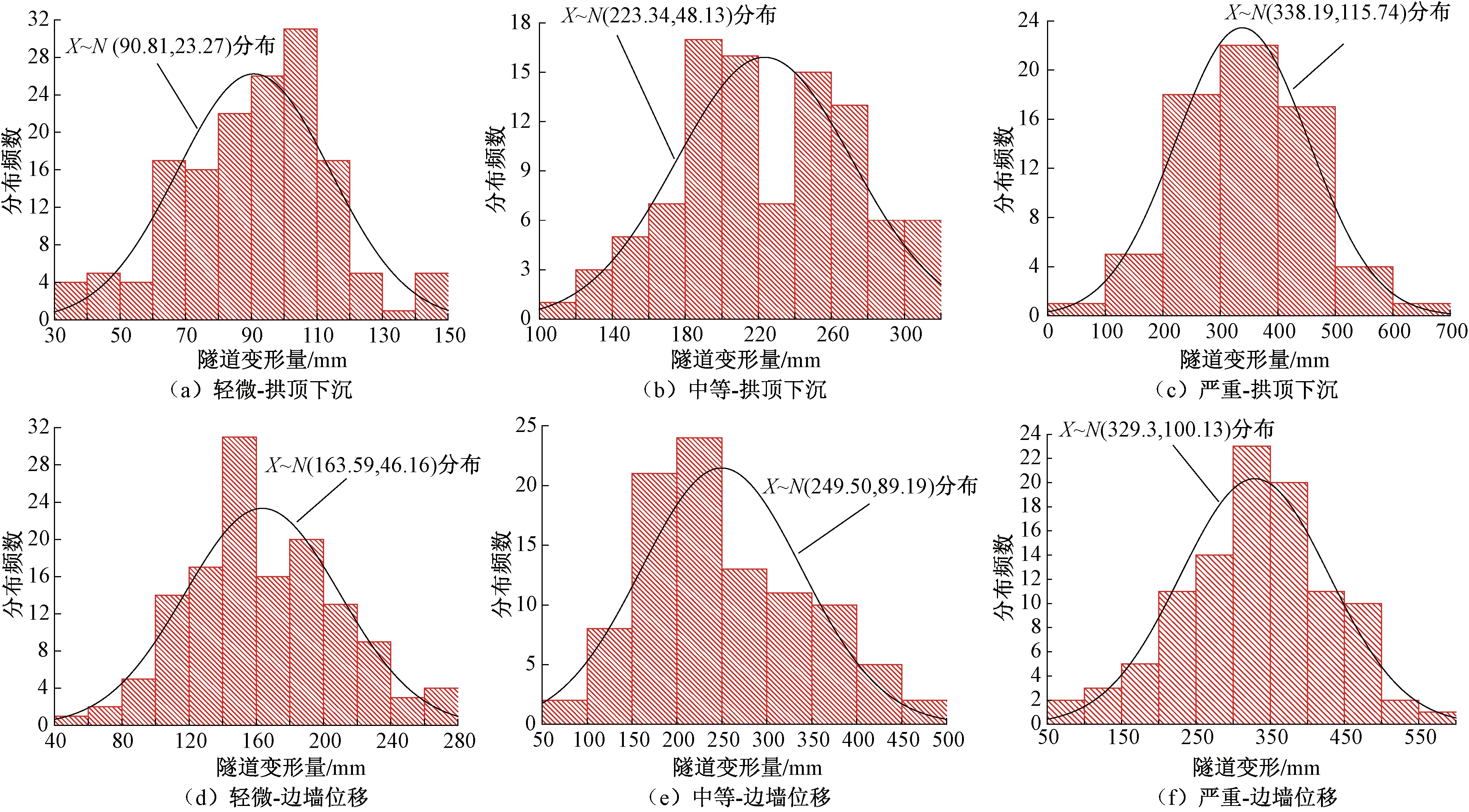
圖25 單線隧道變形分布直方圖

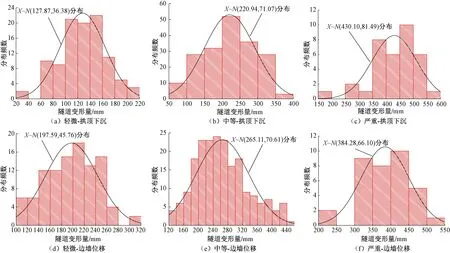
圖26 雙線隧道變形分布直方圖

由圖25、圖26可知，在顯著性水平為0.05水平下，通過回歸方程的顯著性檢驗，雖然部分變形量級存在缺失，但某一大變形等級下隧道變形量統計數據顯著性地來自正態分布總體。隧道變形量分布頻數在某一范圍內相對集中，通過分布擬合公式及置信區間的計算公式，隧道變形量平均值及95%置信區間上、下限見表9。

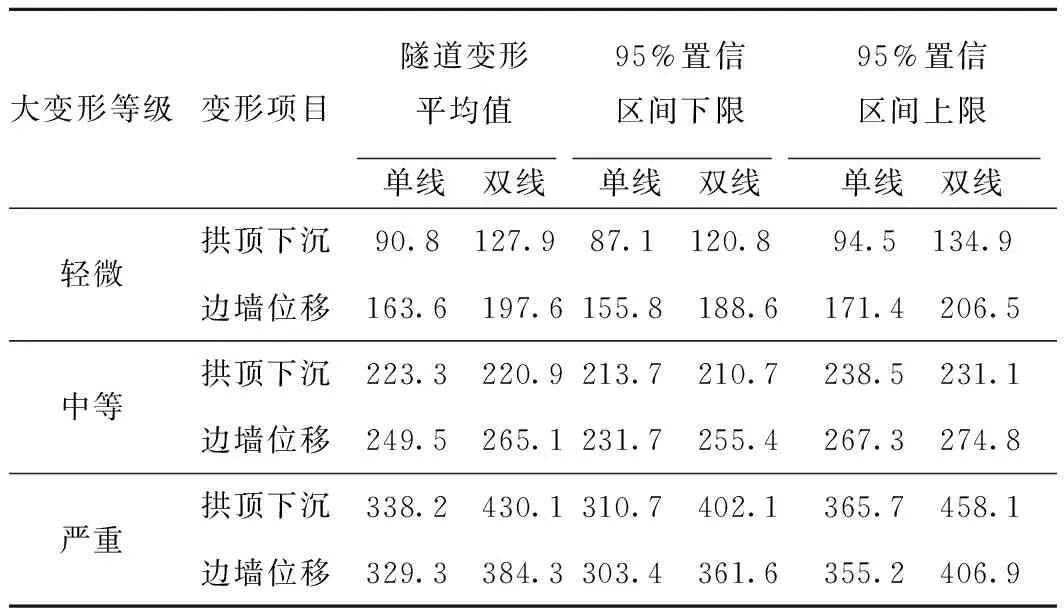
表9 隧道變形量置信區間計算結果 cm

由表9可知，隨著變形等級的提高，隧道變形量平均值、95%置信區間上、下限不斷增大，而且雙線隧道變形量明顯大于單線隧道。同時，隨著變形等級提高，隧道變形由邊墻位移為主向均勻變形過渡。如單線隧道輕微、中等和嚴重大變形段，拱頂下沉與邊墻位移平均值的比值分別為0.56、0.89和1.03。這主要是隨著大變形等級的提高，隧道埋深逐漸加大，地應力分布向靜水壓力分布規律變化，同時隧道斷面向圓形過渡，邊墻位移優勢逐漸減小。

5.2 隧道預留變形確定

基于實測數據統計值，考慮量測丟失位移(15%)[42,57]，取拱頂下沉的下限和邊墻邊移的上限，參考其他工程經驗，對統計結果進行適當調整。其中極嚴重大變形段缺乏統計數據，但為與大變形分級相對應，根據隧道變形量隨大變形等級提高而逐漸增大的規律，取嚴重大變形段隧道預留變形量上限作為極嚴重大變形段預留變形量的下限，最終成蘭鐵路軟巖隧道預留變形量見表10。

表10 隧道預留變形量建議值 cm

5.3 基于施工過程的變形控制基準

上述預留變形量為隧道變形控制總量，但隧道變形隨開挖逐漸增大。根據上述各施工階段變形占比分析，當地質條件、支護參數及開挖方法確定時，某一施工階段變形量與總變形量的比值相對集中于一數值。即以預留變形量為隧道變形控制的總基準，當某一階段累計變形占比超過總基準的一定變形比例，則推測隧道最終變形量可能會超過預留變形量，造成初支侵限。以嚴重大變形段為例進一步說明，隧道采用三臺階法開挖，根據圖23及表8可知，大量數據統計結果表明，當中臺階開挖至監測斷面時，S1-1及S1-2變形占比平均值為42.4%。如監測斷面S1-1或S1-2在中臺階開挖前變形占比大于42.4%，則根據變形隨臺階開挖的發展規律，在不采取其他措施的情況下，當隧道開挖完成后最終變形量會超過預留變形量。同時當下臺階開挖時變形占比超過中、上臺階開挖時累積變形占比68.4%時，則最終變形量極有可能超過預留變形量。

基于上述思路及不同大變形等級下隧道施工過程變形規律，將邊墻位移作為控制目標，以預留變形量為總基準，以施工階段累計變形占比作為過程控制基準，成蘭鐵路軟巖隧道位移控制基準見表11，其中極嚴重大變形段參考嚴重大變形段。其中輕微大變形段采用二臺階帶仰拱開挖方法，中等大變形段采用二臺階開挖方法，嚴重與極嚴重大變形段采用三臺階開挖方法。

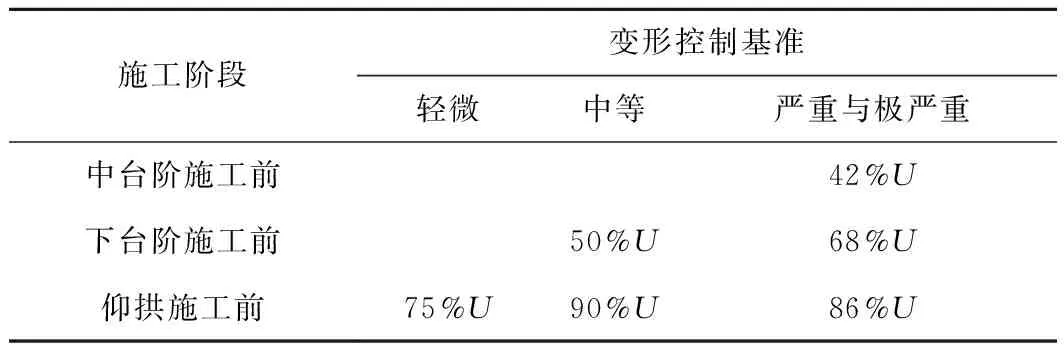
表11 基于施工過程的隧道變形控制基準

隧道大變形應進行過程干預，分階段控制，表11的意義在于施工過程中通過監控量測對隧道變形進行預測，在隧道變形即將達到階段變形標準前及時采取措施，從而有效控制隧道變形，避免初支侵限的發生。

6 工程試驗驗證

6.1 工程驗證試驗段

為了進一步驗證軟巖隧道變形控制體系的適用性，業主單位聯合設計、監理、科研及施工單位，開展了大變形控制工程試驗驗證。基于上述控制體系，分別選取楊家坪隧道、茂縣隧道作為試驗點，每個試驗段長度為40 m，試驗段具體信息見表12。

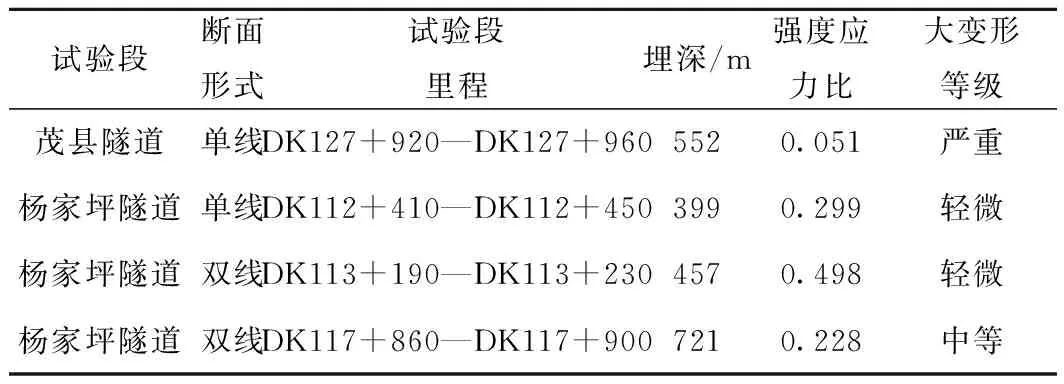
表12 工程應用試驗段大變形分級結果

6.2 應用效果分析

以隧道變形為主要考察目標，各工程應用試驗段典型斷面變形時程曲線見圖27。

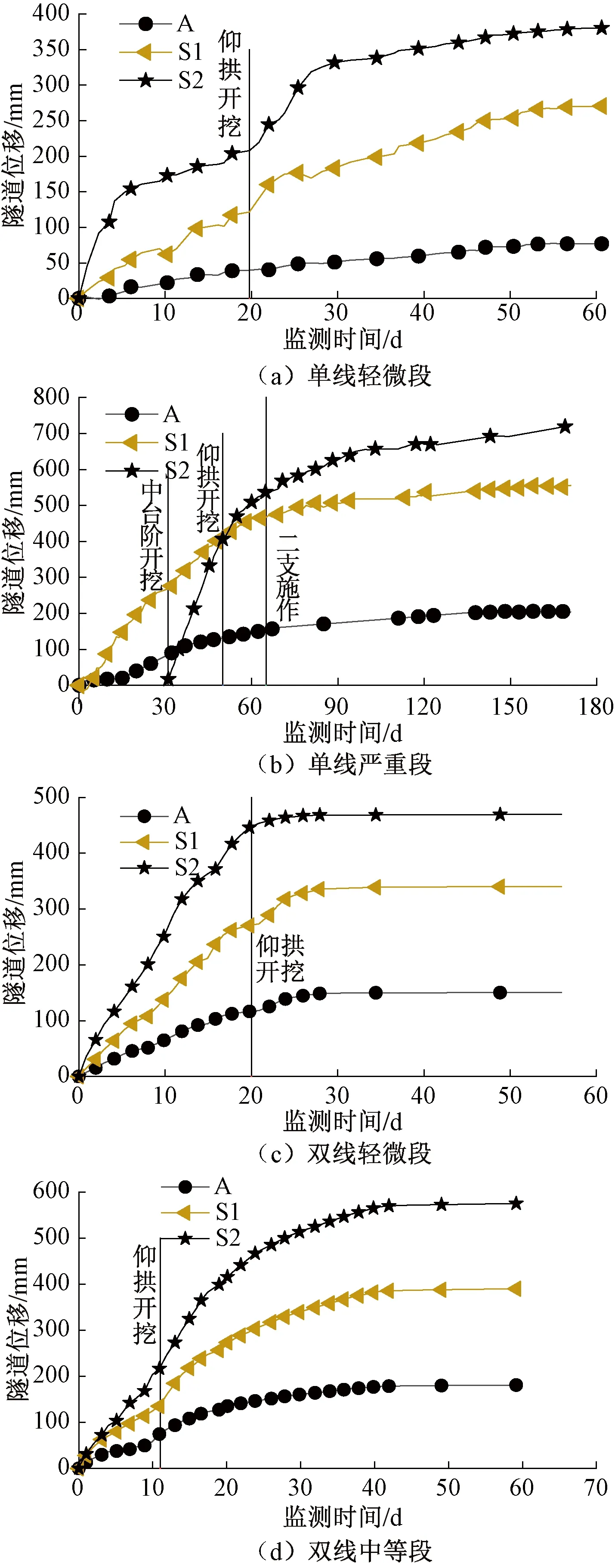
圖27 典型隧道變形時程曲線

由圖27可知，隧道變形時程規律符合典型的快速增長-減速增長和穩定階段的變化規律。但隨著大變形等級提高，隧道變形量逐漸提高，變形穩定時間逐漸增長，變形在初支封閉后經歷一定時間增長后逐漸趨于穩定。

以邊墻收斂S2為目標，對試驗段變形量進行統計，隨里程分布見圖28。單線輕微段、單線嚴重段、雙線輕微段、雙線中等段隧道邊墻收斂最大值分別為389.4、896.0、481.2、575.5 mm，分別占預留變形量的97.40%、99.56%、96.24%、95.90%；平均值分別為339.6、698.0、417.2、507.0 mm，分別占預留變形量的84.90%、77.56%、83.44%、84.50%。單線嚴重段由于圍巖條件的復雜性及三臺階法開挖的復雜性，變形離散性更大，邊墻收斂平均值與預留變形量之比較低，其他三個試驗段邊墻收斂平均值與預留變形量之比均在80%以上。由此可知，隧道預留變形得到了充分利用，同時未出現初支侵限，隧道變形得到有效控制，支護效果良好。

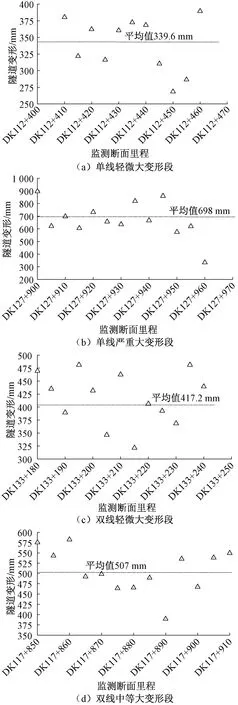
圖28 隧道邊墻收斂隨里程分布圖

7 結論

通過對成蘭鐵路軟巖隧道變形控制技術總結和變形量測數據統計分析，提出軟巖隧道變形控制技術及變形控制基準，得出結論如下：

(1)錨桿為控制軟巖隧道變形的關鍵措施之一，宜采用全長黏結式錨桿，配備專用機械化設備，隨大變形等級提高，逐漸增大錨桿長度，其中嚴重和極嚴重大變形段采用長短組合錨桿，實現錨桿的快錨固，早承載。

(2)針對不同大變形等級，逐漸優化隧道斷面，盡量采用大斷面開挖，既可以減少圍巖擾動，又可以減少空間限制對長錨桿施作的影響，從而控制圍巖變形，提高施工效率，二襯作為安全儲備，在初支變形穩定后施作，保證結構的長期穩定性。

(3)基于主動控制的軟巖隧道支護理念，成蘭鐵路提出“優化斷面，強化錨桿，減少開挖分步，動態調整，分級控制”的軟巖隧道大變形控制技術，現場應用取得了良好的效果。

(4)高地應力軟巖隧道變形受巖體強度應力比及開挖方法影響明顯，不同大變形等級下隧道變形量具有一定的離散性，但隧道變形量整體服從正態分布，考慮爆破至變形監測采集時間段的丟失位移，基于95%的區間估計確定隧道預留變形量的方法具有較強的工程應用性。

(5)基于變形數據統計分析，建議成蘭鐵路輕微大變形段、中等大變形段、嚴重大變形段和極嚴重大變形段單線隧道預留變形量分別為10～20、25～35、35～45、大于45 cm，雙線隧道預留變形量分別為20～30、25～40、40～60、大于60 cm。

(6)考慮大變形分級和開挖方法，基于隧道施工過程建立高地應力千枚巖隧道變形控制基準，通過監控量測實時監測隧道變形，及時采用措施，可以有效防止初支侵限。