基于慣量響應支撐功率的電力系統一次調頻功率估算

秦毅，劉國海

(江蘇大學 電氣信息工程學院，江蘇 鎮江 212000)

0 引 言

近年來，傳統的發電方式逐漸被風力、太陽能等新能源發電方式所取代，中國部分地區的新能源發電出力占比已超過50%[1-3]。由于新能源滲透率的提高以及HVDC的大規模接入，電力系統逐漸呈現出弱慣量的特征。同時，電力系統的一次調頻能力逐漸下降，進一步影響到系統的頻率穩定。

慣量響應與一次調頻響應是頻率響應中尤為重要的環節。在新能源電力系統中，諸如風力、太陽能等發電方式采用了電力電子器件并網，造成了發電側與電網側的解耦，使得電力系統中的慣量響應能力降低[4-5]。為了最大化利用資源，新能源機組并不提供有功備用，長期處于最大功率追蹤的控制方式，系統的一次調頻能力隨之降低[6]。由于慣量、一次調頻能力的下降，系統頻率特性惡化，反過來制約新能源發電的規劃[7]。

目前，國內外學者針對慣量響應和一次調頻響應展開了大量的研究。文獻[8-9]從發電機的動力學方程入手，對電力系統的慣量進行了估算，量化了慣量響應中功率支撐的能力。慣量的估算為新能源的規劃問題以及系統頻率穩定提供了理論基礎。針對新能源電力系統中慣量水平較低的情況，文獻[10-11]展開了對虛擬同步機(Virtual Synchronous Generator，VSG)的研究。通過在新能源并網控制器中引入虛擬慣量控制技術，VSG具有了類似同步發電機的特性。與同步發電機轉子中慣量對應，VSG中存在著虛擬慣量。VSG的提出使得新能源電力系統的安全穩定水平得到了提升[12-13]。為了使得新能源發電機組具備一次調頻能力，文獻[14-15] 引入了一次/二次調頻、調速技術。因此，高比例新能源并網的運行適應性進一步提升。

上述研究并未對一次調頻功率進行估算。作為頻率響應的重要組成部分，一次調頻響應起著承上啟下的作用。慣量響應可以減緩擾動中頻率變化的速度，為一次調頻響應贏得時間；一次調頻響應為二次調頻響應做準備，使得系統達到新的穩態。對一次調頻功率進行估算，有助于新能源發電的接納以及系統的穩定運行。

論文針對擾動過程中的一次調頻功率進行估算。首先，對電力系統的頻率響應進行了闡述；然后，對系統的慣量支撐功率進行了估算；根據慣量支撐功率估算的結果，計算一次調頻響應功率并繪制成曲線。最后，在Digsilent Powerfactory仿真軟件中以IEEE 10機39節點為模型對一次調頻響應的估算量進行驗證。

1 電力系統頻率響應

電力系統的頻率響應主要包含慣量響應、一次調頻響應和二次調頻響應。慣量響應是維持頻率穩定的第一道防線，起到緩解頻率變化速度的作用。隨后，一次調頻響應頻率，使得系統達到新的穩態。最后，為了實現頻率的無差調節，二次調頻響應頻率。三者大概的作用時間與范圍如圖1所示。一次調頻大約在擾動后2 s開始作用，二次調頻大約在擾動后30 s開始作用[8]。

圖1 頻率響應

1.1 慣量響應

當系統發生擾動時，有功功率不再平衡，初始時刻慣量源釋放或吸收能量向系統注入或析出有功功率，從而達到減緩頻率變化速度的目的，這一過程就是慣量響應。

在低慣量電力系統中，慣量源主要包含三部分[7]。第一部分是傳統發電機所具有的旋轉慣量，它是慣量源主要的形式[16]。旋轉慣量主要存在于發電機的轉子中，其大小與發電機轉子的半徑、質量緊密聯系;第二部分是虛擬慣量[10]，它是新能源電力系統中不可缺少的部分。隨著新能源滲透比例不斷提高，傳統的發電機組逐漸被新能源發電機組所取代。由于電力電子器件的解耦作用，旋轉慣量的大小逐漸減小，系統的慣量水平不足以支撐電網安全穩定運行。此時，通過虛擬慣量控制技術使得并網控制器模擬發電機運行特性，從而提供虛擬慣量[17];第三部分是負荷側慣量[18]，相比于前兩部分的慣量而言，它所占的比例較小，經常容易被忽略。在低慣量電力系統中，負荷側慣量的重要性日益凸顯。

1.2 一次調頻響應

一次調頻響應處于頻率響應的中間環節，是維持頻率穩定的重要因素。當有功功率的不平衡程度較大時且一次調頻超出動作死區時，系統中的一次調頻逐漸響應[19-20]。此時，系統中傳統的發電機組通過調速器調整原動機的出力，從而提高各臺發電機的機械功率。當系統頻率達到最低點時，一次調頻響應達到最大限值。隨著時間的推移，系統的頻率逐漸恢復穩態。在新能源電力系統中，一次調頻能力逐漸下降，威脅系統頻率穩定。

1.3 二次調頻響應

為了恢復頻率穩定，系統需要二次調頻響應以實現頻率的無差調節。二次調頻主要由一些調頻廠來承擔，此時發電機的調頻器調整機械功率的輸出。二次調頻響應的作用時間較長，在該階段，頻率逐漸恢復至額定值附近。

2 電力系統頻率響應的功率估算

2.1 慣量響應的支撐功率估算

在有功不平衡的起始階段，電力系統的頻率響應主要是慣量響應。發電機釋放存儲在轉子中的動能或吸收能量，從而改變發電機輸出的電磁功率，阻礙系統頻率波動。

為了衡量電力系統的慣性大小，采用慣性常數作為參考量。慣性常數的大小與頻率變化的快慢成正比[7]。同步發電機的慣性常數定義為額定轉速下轉子的動能與發電機額定容量的比值，表達式如下：

(1)

式中J為發電機的轉動慣量；ωgn為發電機的額定電角速度；Sgn為發電機的額定容量。

根據能量守恒定理，存在系統等值慣性常數，其表達式如下：

(2)

式中N為系統中發電機的個數；Hsys為系統等值慣性常數；Hg,i為發電機i的慣性常數；Sgn,i為發電機i的額定容量；Ssys為系統的發電機額定容量。

在慣量響應的過程中，由于系統等值慣性常數的存在，系統頻率不會發生突變。在該過程中，慣量響應提供的支撐功率隨時間變化[21]如下：

(3)

(4)

式中Pine為慣量響應提供的支撐功率；fCOI為中心頻率；fi為發電機i節點的頻率。

2.2 一次調頻的功率估算

當系統頻率超出各臺發電機的調頻死區后，一次調頻開始介入。此時，一次調頻響應開始調整原動機輸出的機械功率，不斷地減小系統中的有功不平衡。當頻率達到最低點，一次調頻功率的瞬時值達到最大。由此可見，一次調頻功率也是一個隨時間變化的量。系統的有功不平衡主要由慣量響應提供的支撐功率以及一次調頻功率共同彌補：

ΔP(t)=Pine(t)+Ppri(t)

(5)

式中 ΔP(t)為系統t時刻的有功不平衡值；Ppri(t)為系統t時刻的一次調頻功率。

結合式(3)和式(5)，則有一次調頻功率估算表達式如下：

(6)

由式(6)可見，根據慣量響應提供的支撐功率估算值，可以計算一次調頻功率。

2.3 一次調頻功率估算的步驟

(1)統計系統中各臺發電機的慣性常數、額定容量，并計算系統的等值發電機慣性時間常數；

(2)采樣擾動后各個發電機節點的頻率以及系統的有功不平衡大小；

(3)按照式(6)估算擾動后各個時刻的一次調頻功率，并將其繪制成曲線Ppri-t。橫坐標為時間，縱坐標為一次調頻功率大小。具體流程圖如圖2所示。

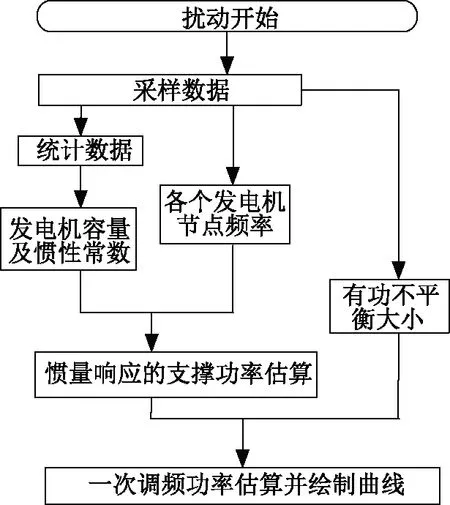
圖2 一次調頻功率估算的流程圖

3 仿真驗證

3.1 仿真模型

為了驗證采用所提方法估算電力系統一次調頻功率的準確性，論文采用10機39節點系統作為仿真模型，仿真軟件為Digsilent Powerfactory。其中，G01為外部電網等值機，G02為平衡機。具體模型如圖3所示，各臺發電機的額定容量及慣性常數見表1。

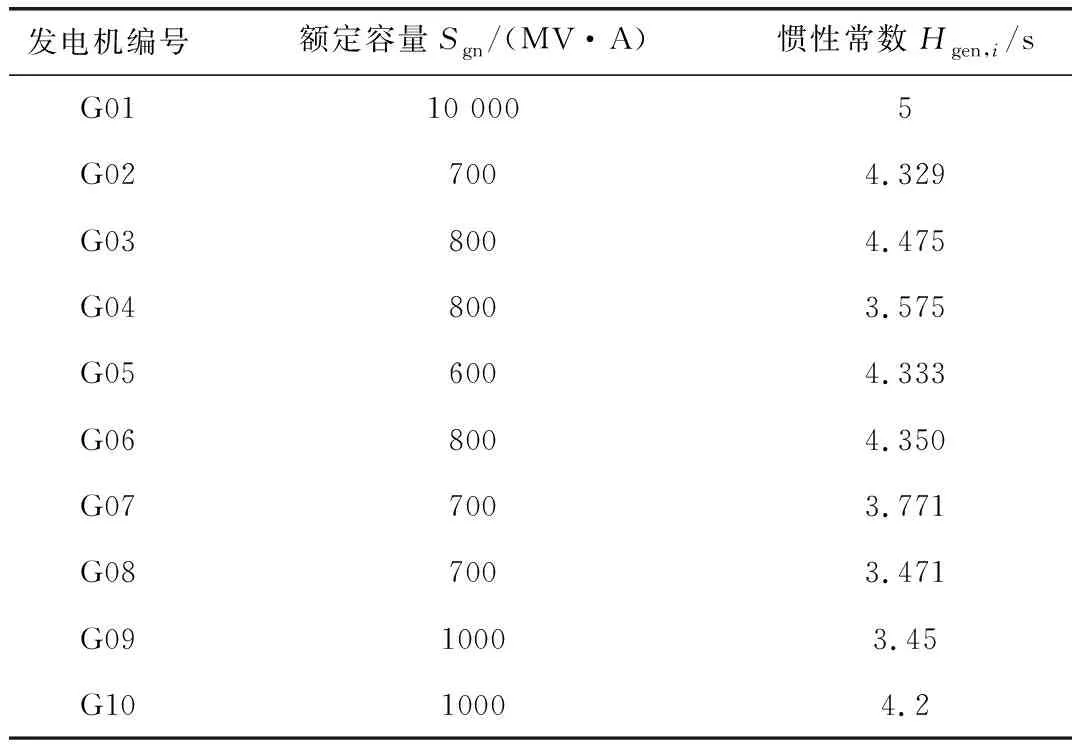
表1 發電機額定容量和慣性常數

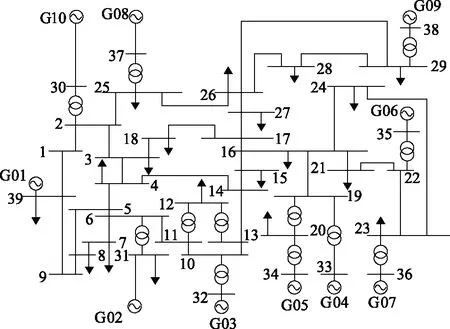
圖3 10機39節點系統

3.2 一次調頻功率估算驗證

由于一次調頻響應存在著死區，擾動較小時，系統主要由慣量響應維持頻率在正常的波動范圍內。因此，論文仿真驗證環節均采用發電機停機事件，共設置3個場景，分別為：

場景1：發電機G03停機，擾動大小為650 MW；

場景2：發電機G04停機，擾動大小為632 MW；

場景3：發電機G05停機，擾動大小為508 MW；

按照式(3)，可以估算三種不同發電機停機事件下慣量響應所提供的支撐功率，如圖4所示。G03～G05停機事件下的慣量響應支撐功率曲線對應于圖中的實線、虛線、點畫線。

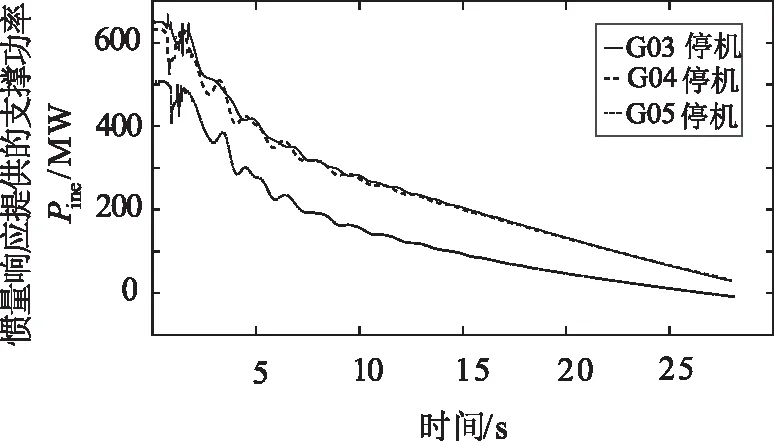
圖4 慣量響應的支撐功率

在擾動發生初始階段，頻率響應主要是慣量響應，系統中所有的慣量源釋放能量以提高輸出的電磁功率彌補有功缺額。由圖4可見，該階段慣量響應提供的支撐功率與有功缺額的大小基本一致。隨著時間的推移，慣量響應所提供的支撐功率不斷減小并逐漸接近于0。

根據式(6)以及圖3繪制的慣量響應支撐功率，可以估算出系統一次調頻功率曲線。為了判斷估算出的一次調頻功率曲線的誤差，本節將估算出的一次調頻功率曲線與仿真中系統實際的一次調頻功率曲線做對比，如圖4～圖6所示。同時，在各個時刻下，計算一次調頻功率的估算誤差，并做平均化處理，見表2。誤差公式如下：

(7)

式中Ppri(t)為系統t時刻估算的一次調頻功率；Ppri’(t)為系統t時刻實際的一次調頻功率；NT為采樣數目(采樣間隔為0.01 s)。

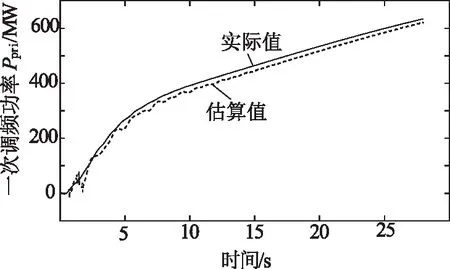
圖5 G03停機時的一次調頻功率曲線

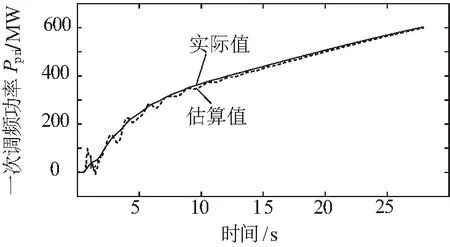
圖6 G04停機時的一次調頻功率曲線

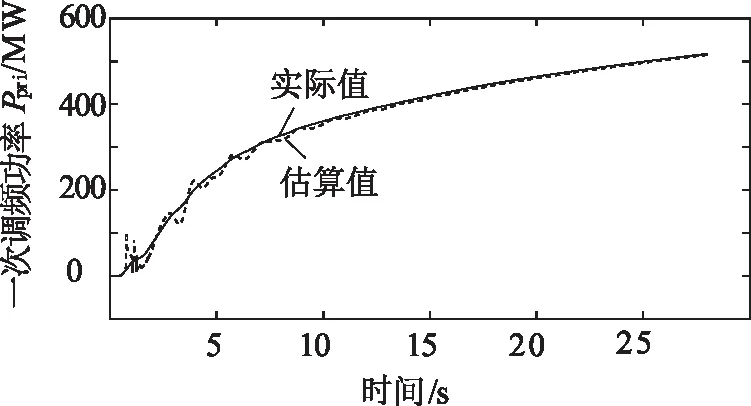
圖7 G05停機時的一次調頻功率曲線

由圖5～圖7可見，在不同的發電機停機事件下，采用論文方法估算出的一次調頻功率曲線與仿真環境下實際的一次調頻功率曲線基本一致。擾動初始階段，由于動作死區的存在，一次調頻功率基本為0。隨著時間的變化，一次調頻功率逐漸提高，一次調頻響應成為系統主要的頻率響應，阻礙系統頻率持續跌落。由表2可見，估算的一次調頻功率平均誤差相對較小，最小為5.51%，最大為7.32%。因此，采用論文所提的方法可以估算并繪制系統一次調頻功率曲線。

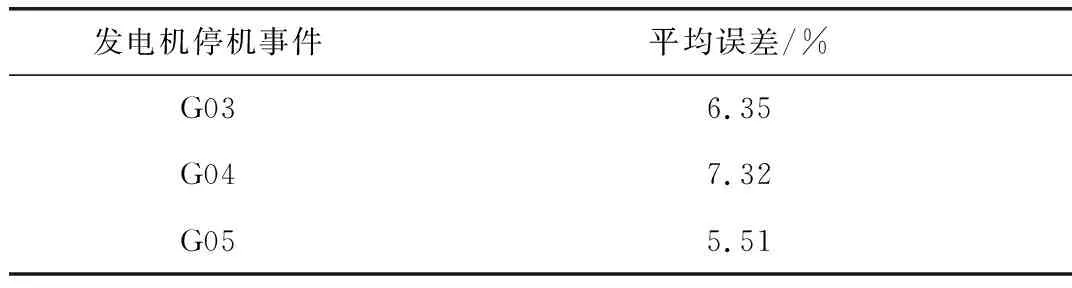
表2 一次調頻功率平均誤差

4 結束語

論文針對電力系統的一次調頻功率展開了研究，闡述了頻率響應的過程。通過估算慣量響應所提供的支撐功率，可以計算并繪制出一次調頻功率曲線。最后在Digsilent Powerfactory仿真軟件下的10機39節點系統中得到了驗證。主要結論如下：

(1)擾動中的有功缺額主要由慣量響應所提供的支撐功率以及一次調頻功率共同彌補。通過估算慣量響應所提供的支撐功率，可以有效得到一次調頻功率曲線;

(2)通過采集部分節點的頻率以及系統的有功缺額即可估算一次調頻功率。這種方法不需要對每一臺發電機的一次調頻性能進行測試，相對簡單、高效，且易于實現。